경사 하강법 (Gradient Descent)
경사하강법은 함수 값이 낮아지는 방향으로 독립변수의 값을 변형시켜가면서 최종적으로 최소 함수 값을 갖도록 하는 독립 변수의 값을 찾는 방법이다.
쉽게 말하자면 앞이 보이지 않는 안개가 낀 산을 내려올 때는 모든 방향으로 산을 더듬어가며 산의 높이가 가장 낮아지는 방향으로 한 발씩 내딛어 최종적으로 산을 내려오는 것이라고 할 수 있다.
경사하강법이 모델 학습에 쓰이는 이유
우리는 보통 함수의 최솟값을 찾고자 할 때, 미분계수를 구함으로써 찾곤 한다(컴퓨터를 사용하는 것이 아닌 그냥 수학 문제를 풀 때). 컴퓨터에서 해당 방법을 사용하지 않는 이유는 다음과 같다.
-
실제 분석에서(특히, 딥러닝 알고리즘을 활용하는 경우) 보게 되는 함수들은 형태가 굉장히 복잡해서 미분계수와 그 근을 계산하기 어려운 경우가 많기 때문에
-
미분계수 계산 과정을 컴퓨터로 구현하는 것보다, 경사하강법을 구현하는 것이 훨씬 쉽기 때문에
-
데이터의 양이 매우 큰 경우 경사하강법과 같은 순차적인 방법이 계산량 측면에서 훨씬 효율적이기 때문에
경사 하강법 알아보기
경사하강법은 함수의 기울기를 이용해 의 값을 어디로 옮겼을 때 함수가 최소값을 갖는지 알아보는 방법이다.
기울기가 양수라는 것은 $x$의 값이 커질수록 함수 값이 커진다는 것을 의미하고, 기울기가 음수라면 $x$의 값이 커질수록 함수의 값이 작아진다는 것을 의미한다.
기울기의 값이 크다면 가파르다는 것을 의미하기도 하지만, 또한 $x$의 위치가 최소값에 해당되는 $x$좌표로부터 멀리 떨어져 있다는 것을 의미하기도 한다.
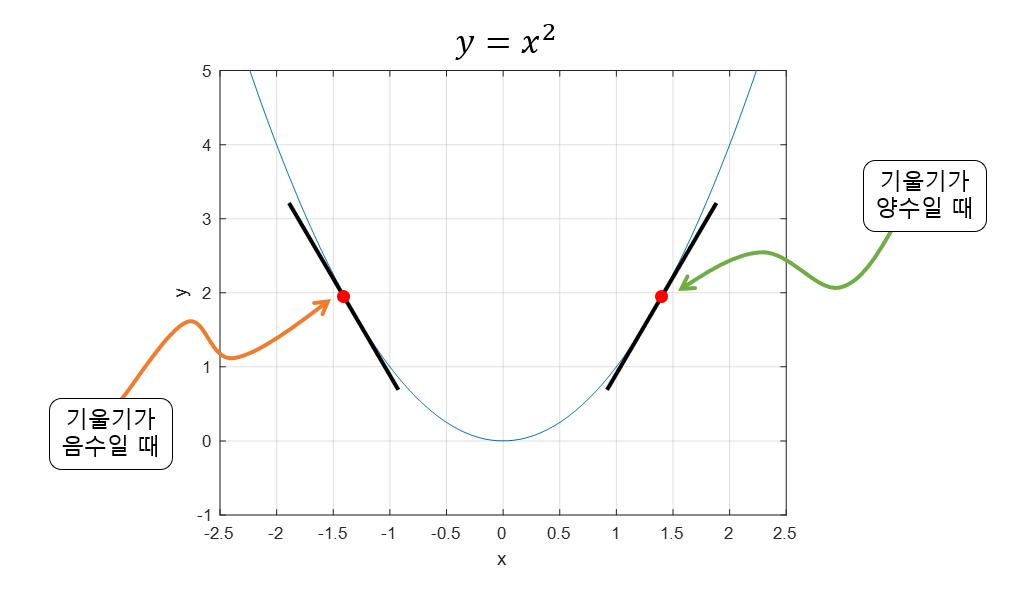
경사하강법의 방향성분
특정 포인트인 좌표에서 가 커질수록 함수값이 커지는 중이라면 즉, 기울기가 양수라면 양의 방향으로 를 옮겨야하고, 반대로 특정 포인트인 좌표에서 가 커질수록 함수값이 작아지는 중이라면 즉, 기울기의 부호가 음수라면 양의 방향으로 를 옮기면 된다.
위의 논리에 대한 식은 다음과 같다.
= 번째 계산된 의 좌표
= 번째 계산된 좌표
경사의 크기
미분계수 즉, 기울기 값은 극소값에 가까울수록 그 값이 작아진다.
따라서 이동거리에 사용할 값을 기울기의 크기와 비례하는 인수를 이용하면 의 값이 극소값에서 멀 때는 많이 이동하고, 극소값에 가까워졌을 때는 조금씩 이동할 수 있게 된다.
즉 이동거리는 기울기 값을 직접 이용하되, 사용자가 이동거리를 적절히 조절할 수 있도록 수식을 조정해줌으로써 상황에 맞게 이동거리를 맞춰나갈 수 있게 하면 된다.
이동거리(step_size) 또는 머신러닝에서는 학습률(learning_rate)이라고 한다.라고 부르고 기호는 보통 로 사용한다.
경사하강법 알고리즘
- 모든 데이터 포인트에서 파라미터()에 대해 기울기 값을 계산한다.
에 대해 함수 미분후 데이터에 값 대입) - 1에서 구한 기울기에 대한 평균을 낸다.
- 를 다음과 같이 업데이트 한다.
- 수렴할 때까지 반복한다.
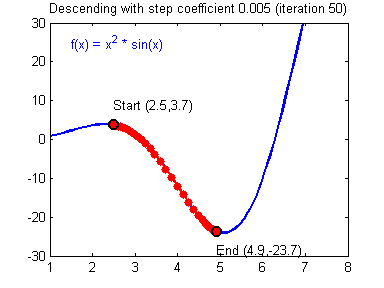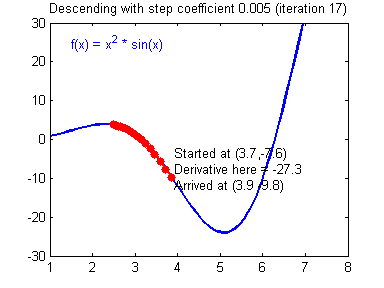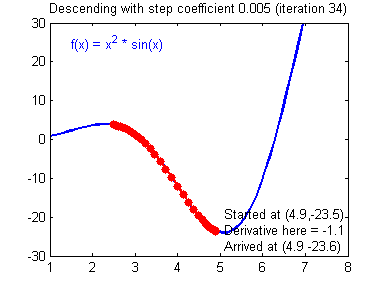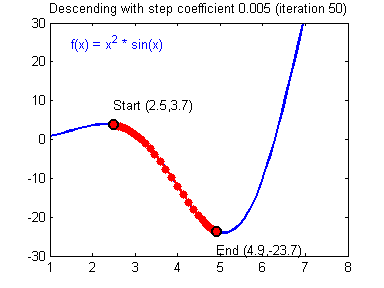
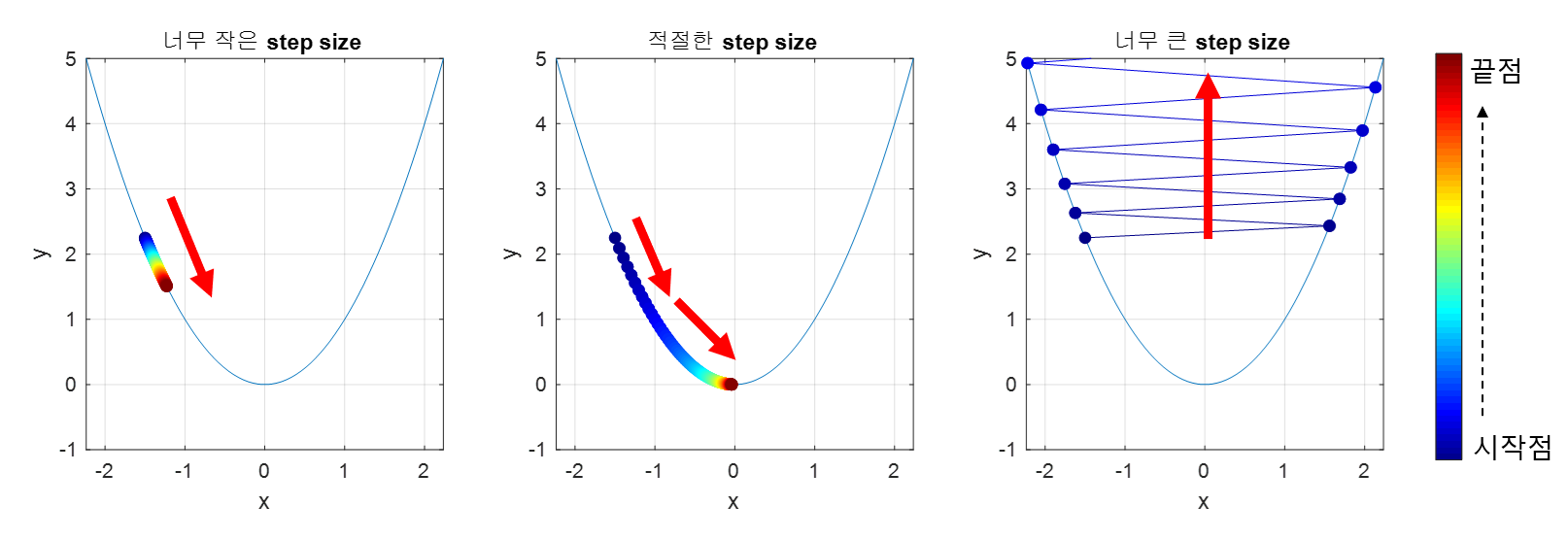
이동거리 설정
이동거리를 크게 설정한 경우 빠르게 최소값에 수렴한다는 장점이 있지만, 이동거리를 너무 크게 설정하게 되면 수렴되지 못하고 함수 값이 계속 커지는 방향으로 최적화가 진행될 수 있다.
만약 너무 작게 설정한다면 최소값을 수렴하는데 소요시간이 오래 걸린다는 단점이 있다.
적절한 이동거리를 설정하는 것이 중요하다.
지역 최소점(local minimum)
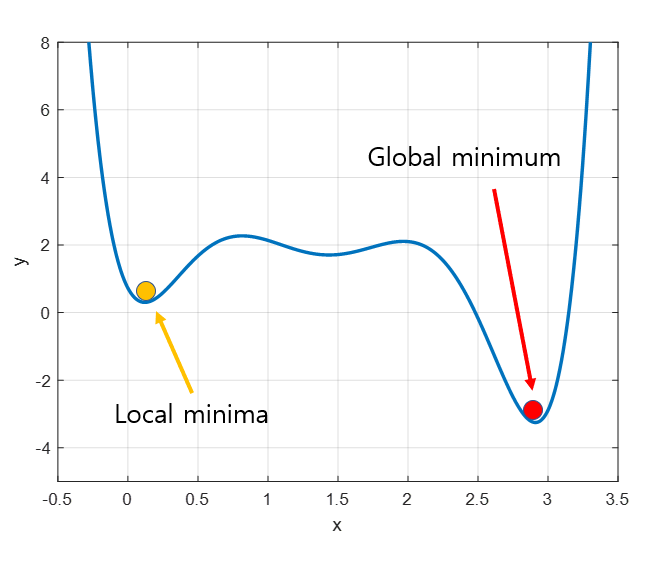
경사하강법 알고리즘의 시작 위치는 매번 랜덤하기 때문에 어떤 경우에는 지역 최소점에 빠져 전역 최소점(global minimum)에 도달하지 못하는 경우가 생긴다.
하지만 최근에는 실제로 딥러닝이 수행될 때 지역 최소점에 빠질 확률이 거의 없다고 한다. 위의 그래프는 가중치 하나의 경사하강법 그래프 이지만 딥러닝에서 사용되는 가중치의 수는 수도 없이 많고, 모든 가중치가 지역 최소점에 빠져야 가중치 업데이트가 종료된다. 이는 이론적으로 거의 불가능에 가까운 일이므로 지역최소점을 고려할 필요가 없다고 봐도 무방하다고 볼 수 있다.
