[딥러닝] 역전파 (Backpropagation)

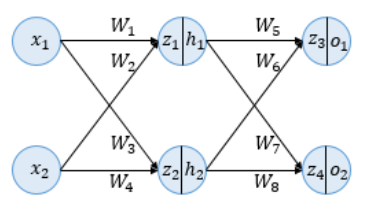
순전파 (Forward Propagation)

입력받은 데이터를 각 가중치와 곱하고 은닉층과 출력층의 활성화 함수를 통해 예측값을 출력한다.

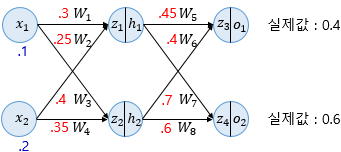
이미지 출처 : https://wikidocs.net/37406

활성화 함수는 시그모이드 함수로 정의함.
activation = 'sigmoid'

시그모이드 함수

$sigmoid = S(x) = \frac{1}{1+e^{-x}}$

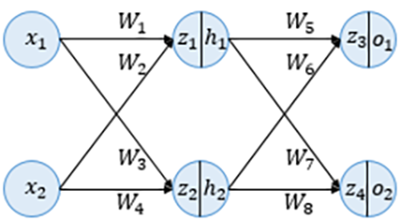
첫번째로 입력층으로 입력된 데이터는 은닉층 방향으로 향하면서 가중치와 곱해져 시그모이드 함수의 입력값 $z_1$, $z_2$가 된다.

$z_1 = W_1x_1 + W_2x_2 = 0.3 \times 0.1 + 0.25 \times 0.2 = 0.08 \\{}\\ z_2 = W_3x_1 + W_4x_2 = 0.4 \times 0.1 + 0.35 \times 0.2 = 0.11$

가중합으로 계산된 $z_1$, $z_2$는 은닉층의 시그모이드 함수의 입력값이 되며 함수를 통해 출력되는 값이 은닉층의 최종 출력값 $h_1$, $h_2$가 된다.

$h_1 = sigmoid(z_1) = 0.51998934 \\{}\\ h_2 = sigmoid(z_2) = 0.52747230$

은닉층에서 출력된 $h_1$, $h_2$는 다시 출력층 방향으로 향하면서 가중치와 곱해지게 되고 출력층의 입력값 $z_3$, $z_4$가 된다.

$\begin{aligned} z_3& = W_5h_1 + W_6h_2 = 0.45 \times h_1 + 0.4 \times h_2 = 0.44498412 \\{}\\ z_4& = W_7h_1 + W_8h_2 = 0.7 \times h_1 + 0.6 \times h_2 = 0.68047592 \end{aligned}$

은닉층에서 출력층으로 향하면서 가중합으로 계산된 $z_3$, $z_4$는 출력층의 활성화 함수인 시그모이드의 입력값이 되고 함수를 통해 출력된 값은 최종 예측값이 된다.

$\begin{aligned} o_1& = sigmoid(z_3) = 0.60944600\\{}\\ o_2& = sigmoid(z_4) = 0.66384491 \end{aligned}$

출력된 예측값에서 실제값과의 오차를 계산하기 위한 손실 함수(Loss function)로 평균 제곱 오차인 MSE 를 사용한다. 손실 함수를 통해서 우리는 예측값이 실제값과의 차이를 판단하여 모델 학습이 얼마나 잘 되었는지 판단할 수 있다. 식에서는 실제값은 target, 예측값은 output으로 표현된다. $E_{o_1}$, $E_{o_2}$ 는 각각의 예측값과 실제값에 대한 오차이다.

$E_{o_1} = \frac{1}{2}(target_{o_1} - output_{o_1})^2 = \frac{1}{2}(0.4 - 0.60944600)^2 = 0.02193381 \\{}\\ E_{o_2} = \frac{1}{2}(target_{o_2} - output_{o_2})^2 = \frac{1}{2}(0.6 - 0.66384491)^2 = 0.02193381 \\$

$E_{o_1}$, $E_{o_2}$인 각 오차의 합은 다음과 같다.

$E_{total} = E_{o_1} + E_{o_2} = 0.02397190$

위의 값을 토대로 역전파를 진행해보겠다.

역전파 (Backpropagation)

역전파란 오차 역전파법 알고리즘이라고도 하며 동일 입력층에 대해 원하는 값이 출력되도록 각 계층의 가중치를 조정하는 방법이다. 예측값과 실제값의 차이인 오차를 계산하여 이것을 다시 역으로 전파하여 가중치를 조정한다.

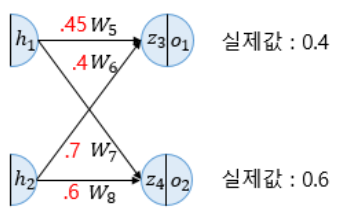
이미지 출처 : https://wikidocs.net/37406

역전파는 순전파의 반대방향으로 즉, 출력층에서 입력층까지 역으로 나아간다.
최종적으로 업데이트가 필요한 가중치는 $W_1$, $W_2$, $W_3$, $W_4$, $W_5$, $W_6$, $W_7$, $W_8$로 총 8개다.

출력층부터 시작되기 때문에 먼저 업데이트 되는 가중치는 $W_4$, $W_5$, $W_6$, $W_7$, $W_8$이다. 가중치를 업데이트 하기 위해서 경사 하강법을 사용한다.
가중치 $W_5$를 업데이트 하기 위해서 $W_5$에 대한 편미분을 계산해야 한다.
$\frac{\partial E_{total}}{\partial W_5}$을 계산하기 위해서 연쇄법칙(chain rule)을 적용해서 풀 수 있다.

$\frac{\partial E_{total}}{\partial W_5} = \frac{\partial E_{total}}{\partial o_1} \times \frac{\partial o_1}{\partial z_3} \times \frac{\partial z_3}{\partial W_5}$

일단 첫번째로 $E_{total}$은 순전파를 통해 출력된 전체 평균 오차 제곱합의 합이다. 식을 풀게 되면 다음과 같다.

$E_{total} = \frac{1}{2}(target_{o_1} - output_{o_1})^2 + \frac{1}{2}(target_{o_2} - output_{o_2})^2$

이 값을 $o_1$에 대한 편미분을 하게 되면 다음과 같다.

$\begin{aligned} &\frac{\partial E_{total}}{\partial o_1} = 2 \times \frac{1}{2}(target_{o_1} - output_{o_1})^{2-1} \times \frac{1}{2}({target_{o_2}}^2 - 2target_{o_2}output_{o_2} + {output_{o_2}}^2)\\{}\\ &= (target_{o_1} - output_{o_1}) \times (-1) + 0 \\{}\\ &= -(target_{o_1} - output_{o_1}) \\{}\\ &= -(0.4 - 0.60944600) = 0.20944600 \end{aligned}$

다음으로 $z_3$의 편미분을 계산 한다.
편미분 하기 전에 $o_1$의 식을 확인해면 다음과 같다.

$o_1 = sigmoid(z_3)$

$z_3$을 미분하려면 sigmoid 함수를 편미분 해야한다.
시그모이드 함수를 편미분 하게 되면 다음과 같다.

$\begin{aligned} &f(x) = \frac{1}{1+e^{-x}} = \frac{e^x}{1 + e^x}\\{}\\ &\frac{\partial}{\partial x}f(x) = \frac{e^x \cdot (1 + e^x) - e^x \cdot e^x}{(1+e^x)^2} = \frac{e^x}{(1+e^x)^2} = f(x)(1-f(x)) \end{aligned}$

시그모이드 함수의 편미분 식을 통해서 $z_3$를 편미분한 식은 다음과 같다.

$\frac{\partial o_1}{\partial z_3} = o_1 \times(1 - o_1) = 0.60944600(1-0.60944600) = 0.23802157$

마지막으로 $W_5$의 편미분을 하기 전 $z_3$의 수식을 돌아보면 다음과 같다.

$z_3 = W_5h_1 + W_6h_2 = 0.45 \times h_1 + 0.4 \times h_2$

위 식을 바탕으로 $W_5$에 대해 편미분을 하게되면 $W_6$는 상수취급되어 사라지고 $W_5$가 0승이 되어 사라지기 떄문에 결과적으로 $h_1$만 남게 된다.
식은 다음과 같다.

$\frac{\partial z_3}{\partial W_5} = h1 = 0.51998934$

$h_1$값은 알고 있기 때문에 바로 답을 구할 수 있었다.
모든 값을 구했기 때문에 결과적으로 $\frac{\partial E_{total}}{\partial W_5}$ 값을 구할 수 있게 되었다.

$\frac{\partial E_{total}}{\partial W_5} = 0.20944600 \times 0.23802157 \times 0.51998934 = 0.02592286$

이제 경사하강법을 이용하여 가중치를 업데이트 하게 되는데 학습률(learning rate) $\alpha$는 0.5로 설정하겠다.

$W_5^+ = W_5 - \alpha\frac{\partial E_{total}}{\partial W_5} = 0.45 - 0.5 \times 0.02592286 = 0.43703857$

$W_5$의 가중치가 다음과 같은 방법으로 업데이트 되는 것을 확인할 수 있다.
나머지의 $W_6$, $W_7$, $W_8$ 을 업데이트 하면 다음과 같다.

$\frac{\partial E_{total}}{\partial W_6} = \frac{\partial E_{total}}{\partial o_1} \times \frac{\partial o_1}{\partial z_3} \times \frac{\partial z_3}{\partial W_6} \rightarrow W_6^+ = 0.38685205 \\{}\\ \frac{\partial E_{total}}{\partial W_7} = \frac{\partial E_{total}}{\partial o_2} \times \frac{\partial o_2}{\partial z_4} \times \frac{\partial z_4}{\partial W_7} \rightarrow W_7^+ = 0.69629578 \\{}\\ \frac{\partial E_{total}}{\partial W_8} = \frac{\partial E_{total}}{\partial o_2} \times \frac{\partial o_2}{\partial z_4} \times \frac{\partial z_4}{\partial W_8} \rightarrow W_8^+ =0.59624247$

모두 업데이트가 되었다면 은닉층으로 넘어가서 $W_1$, $W_2$, $W_3$, $W_4$를 업데이트 해보겠다. 아래의 그림은 위에서 업데이트 된 가중치로 바뀐 것을 표현한 것이다.

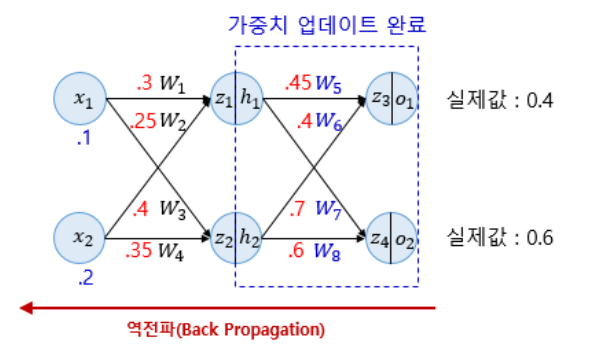
이미지 출처 : https://wikidocs.net/37406

먼저 $W_1$을 업데이트 해보겠다. 위의 했던 과정과 동일하게 편미분을 진행한다.

$\frac{\partial E_{total}}{\partial W_1} = \frac{\partial E_{total}}{\partial h_1} \times \frac{\partial h_1}{\partial z_1} \times \frac{\partial z_1}{\partial W_1}$

우측항의 첫번째 식은 다음과 같다.

$\frac{\partial E_{total}}{\partial h_1} = \frac{\partial E_{o_1}}{\partial h_1} + \frac{\partial E_{o_2}}{\partial h_1}$

위 식에서 우측 첫번째 식에 대해서 분해하여 계산하게 되면 다음과 같다.

$\frac{\partial E_{o_1}}{\partial h_1} = \frac{\partial E_{o_1}}{\partial z_3} \times \frac{\partial z_3}{\partial h_1} = \frac{\partial E_{o_1}}{\partial o_1} \times \frac{\partial o_1}{\partial z_3} \times \frac{\partial z_3}{\partial h_1} \\ {}\\ = -(target_{o_1} - output_{o_1}) \times o_1 \times (1- o_1) \times W_5 \\{}\\ = 0.20944600 \times 0.23802157 \times 0.45 = 0.2243370$

위와 같은 원리로 $\frac{\partial E_{o_2}}{\partial h_1}$을 구하는 식은 다음과 같다.

$\frac{\partial E_{o_2}}{\partial h_1} = \frac{\partial E_{o_2}}{\partial z_4} \times \frac{\partial z_4}{\partial h_1} = \frac{\partial E_{o_2}}{\partial o_2} \times \frac{\partial o_2}{\partial z_4} \times \frac{\partial z_4}{\partial h_1} = 0.00997311 \\$

이제 $\frac{\partial E_{total}}{\partial h_1}$를 구할수 있다.

$\frac{\partial E_{total}}{\partial h_1} = 0.02243370 + 0.00997311 = 0.3240681$

다음으로 $\frac{\partial h_1}{\partial z_1}$에 대해서의 편미분을 구하게 되면 위에서 보았던 sigmoid 함수의 편미분과 같다.

$\frac{\partial h_1}{\partial z_1} = h1 \times (1-h1) = 0.51998934(1-0.51998934) = 0.24960043$

제일 우측항이었던 $\frac{\partial z_1}{\partial W_1}$ 을 구하게 되면 아래의 식과 같다.

$z_1 = W_1x_1 + W_2x_2 = 0.3 \times 0.1 + 0.25 \times 0.2 = 0.08 \\{}\\ \frac{\partial z_1}{\partial W_1} = x_1 = 0.1$

따라서 업데이트 하기 위한 $\frac{\partial E_{total}}{\partial W_1}$은 다음과 같은 식이 된다.

$\frac{\partial E_{total}}{\partial W_1} = 0.03240681 \times 0.24960043 \times 0.1 = 0.00080888$

이제 경사 하강법을 이용해 $W_1$을 업데이트 한다.

$W_1^+ = W_1 - \alpha \frac{\partial E_{total}}{\partial W_1} = 0.1 - 0.5 \times 0.00080888 = 0.29959556$

위와 같은 원리로 $W_2$, $W_3$, $W_4$도 업데이트할 수 있다.

$\frac{\partial E_{total}}{\partial W_2} = \frac{\partial E_{total}}{\partial h_1} \times \frac{\partial h_1}{\partial z_1} \times \frac{\partial z_1}{\partial W_2} \rightarrow W_2^+ = 0.24919112 \\{}\\ \frac{\partial E_{total}}{\partial W_3} = \frac{\partial E_{total}}{\partial h_2} \times \frac{\partial h_2}{\partial z_2} \times \frac{\partial z_2}{\partial W_3} \rightarrow W_3^+ = 0.39964496 \\{}\\ \frac{\partial E_{total}}{\partial W_4} = \frac{\partial E_{total}}{\partial h_2} \times \frac{\partial h_2}{\partial z_2} \times \frac{\partial z_2}{\partial W_4} \rightarrow W_4^+ = 0.34928991$

마지막으로 순전파를 업데이트된 가중치를 통해 진행하여 오차가 감소하였는지 확인해보겠다.

이미지 출처 : https://wikidocs.net/37406

$\begin{aligned} &z_1 = W_1x_1 + W_2x_2 = 0.29959556 \times 0.1 + 0.24919112 \times 0.2 = 0.07979778 \\{}\\ &z_2 = W_3x_1 + W_4x_2 = 0.39964496 \times 0.1 + 0.34928991 \times 0.2 = 0.10982248 \\{}\\ &h_1 = sigmoid(z1) = 0.51993887 \\{}\\ &h_2 = sigmoid(z2) = 0.52742806 \\{}\\ &z_3 = W_5h_1 + W_6h_2 = 0.43703857 \times h_1 + 0.38685205 \times h_2 = 0.43126996 \\{}\\ &z_4 = W_7h_1 + W_8h_2 = 0.67629578 \times h_1 + 0.59624247 \times h_2 = 0.67650625 \\{}\\ &o_1 = sigmoid(z3) = 0.60617688 \\{}\\ &o_2 = sigmoid(z4) = 0.66295848 \\{}\\ &E_{o_1} = \frac{1}{2}(target_{o_1} - output_{o_1})^2 = 0.02125445 \\{}\\ &E_{o_2} = \frac{1}{2}(target_{o_2} - output_{o_2})^2 = 0.00198189 \\{}\\ &E_{total} = E_{o_1} + E{o_2} = 0.02323634 \end{aligned}$

기존의 전체 오차가 0.02397190이였으므로 역전파를 통해 오차가 0.00073556 감소한 것을 확인할 수 있다.
인공신경망의 학습은 순전파와 역전파를 반복하며 오차를 최소화하는 가중치를 찾는다.