다중 선형 회귀
단순선형회귀의 목적은 하나의 독립변수를 가지고 종속변수를 예측하기 위한 회귀모델을 만드는 것이었다면, 다중선형회귀는 n개의 독립변수를 가지고 종속변수를 예측하기 위한 회귀모델을 만드는 것이다.
다중 선형 회귀의 식
다중공산성 (Multicollinearity)
다중공산성이란 회귀 모형에 포함될 설명변수들 사이에 서로 밀접한 상관관계가 있어서 다중 선형 회귀 모델에서 이들 각각의 개별 효과를 파악하기 힘들게 되는 현상
다중 공산성의 문제점
설명변수 각각에서의 단순 선형 회귀 분석에서는 통계적으로 유의할지 몰라도 설명변수들을 모두 고려한 다중 선형 회귀 분석에서는 변수들 모두 종속변수와 관련없는 것으로 나타날 수 있다.
또한 다중공산성이 있는 설명변수들을 모두 회귀 모델이 포함시킨다면 이로부터 추정된 회귀계수를 신뢰할 수 없게 된다.
설명변수들 사이에 상관분석을 시행해 보아 상관계수가 0.8이상이면 다중 공산성이 있음을 의심해 보아야 한다.
회귀모델 평가 지표 (Evaluation metrics)
결정계수 R-Squared (Coefficient of determination)
SSE (Sum of Squares Error, 관측치와 예측치의 차이)
SSR (Sum of Squares due to Regression, 예측치와 평균 차이)
SST (Sum of Squares Total, 관측치와 평균 차이)
과적합(Overfitting)과 과소적합(Underfitting)
일반화(Generalization)
테스트 데이터에서 만들어내는 오차를 일반화 오차라고 한다.
훈련데이터에서와 같이 테스트 데이터에서도 좋은 성능을 내는 모델은 일반화가 잘된 모델이다.
과적합이란
모델이 훈련 데이터에만 특수한 성질을 과하게 학습해 일반화를 못해 결국 테스트 데이터에서 오차가 커지는 현상
과소적합이란
훈련데이터에 과적합도 못하고 일반화 성질도 학습하지 못해, 훈련/테스트 데이터 모두에서 오차가 크게 나오는 현상
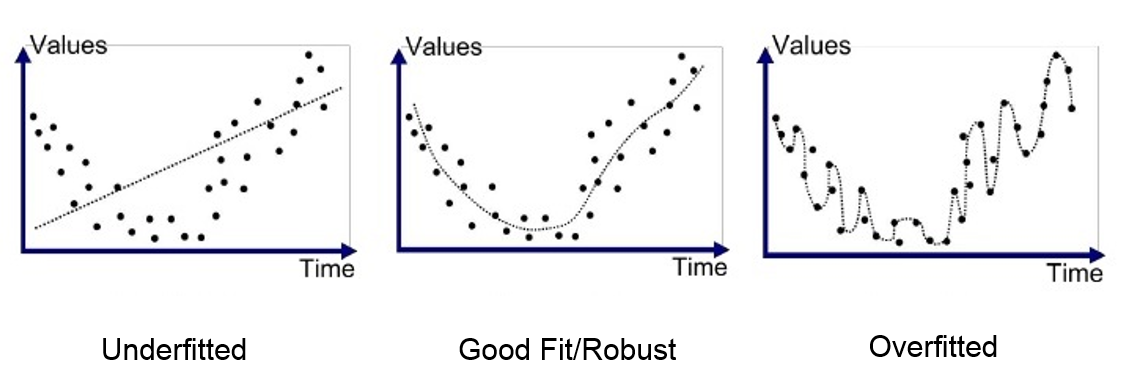
분산(Variance)/편향(Bias) 트레이드 오프
- 분산이 높은경우
모델이 학습 데이터의 노이즈에 민감하게 적합하여 테스트데이터에서 일반화를 잘 못하는 경우 즉 과적합 상태
- 편향이 높은경우
모델이 학습 데이터에서, 특성과 타겟 변수의 관계를 잘 파악하지 못해 과소적합 상태
편향과 분산의 식
편향과 분산의 예시
가정 : 독립변수와 종속변수가 빈선형관계인 모델로 학습해야 하는 데이터 셋
단순선형모델로 학습하는 경우
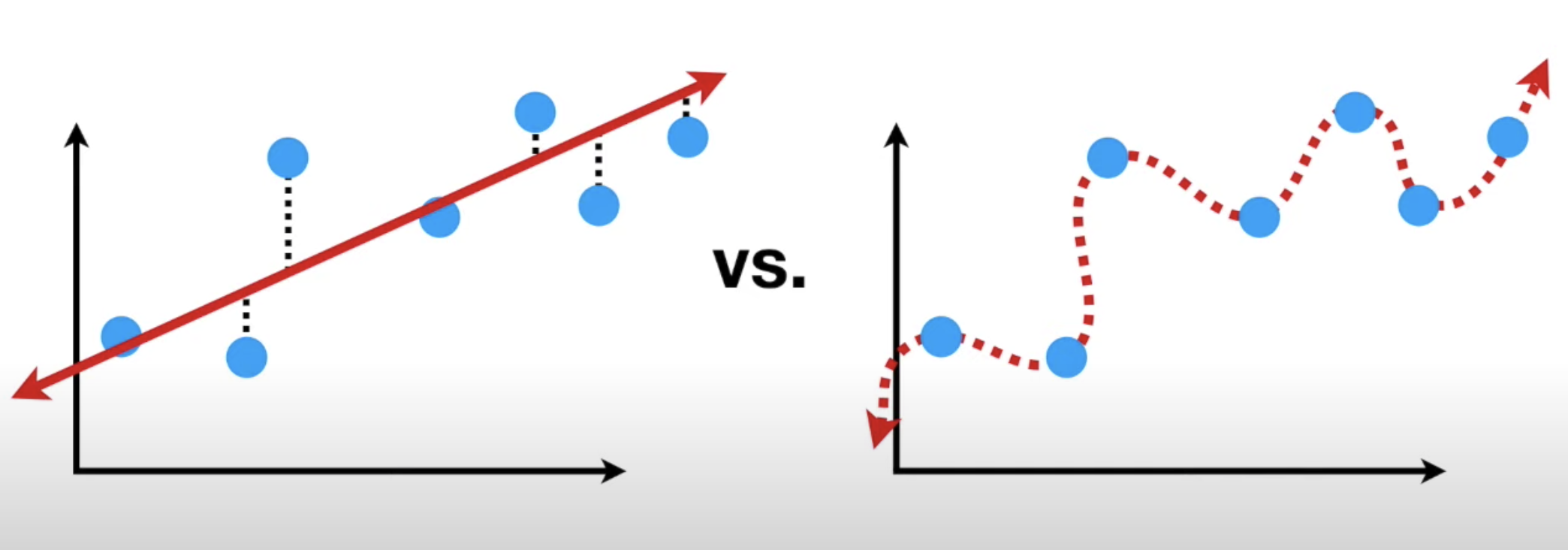
선형모델 예측은 학습데이터에서 타겟값과 오차가 크다.
이를 "편향이 높다"라고하며 과소적합이다.
하지만 훈련/테스트 두 데이터에서 그 오차가 비슷하다.
이를 "분산이 낮다"고 한다.
다중선형모델로 학습하는 경우
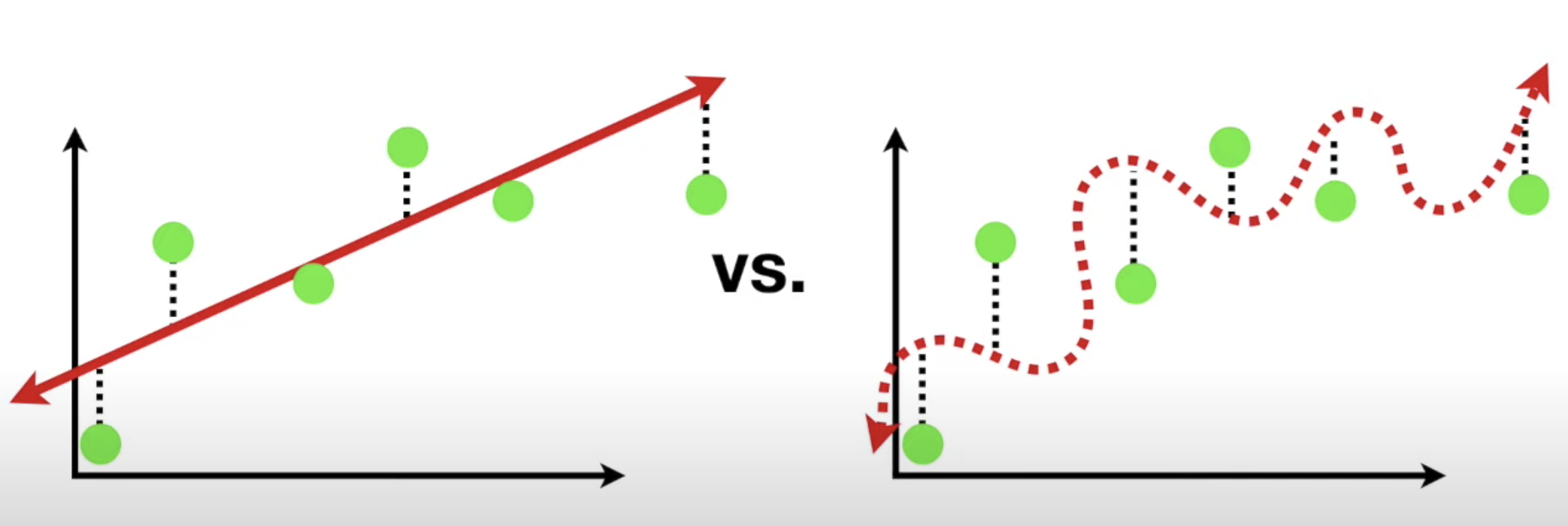
다중선형모델에서는 학습데이터에서 오차가 0에 가깝다.
"편향이 낮다"
하지만 테스트 데이터에서 오차가 많아진다.
"분산이 높다"라고 하며 과적합이라 한다.
