딥러닝
머신러닝 라이브러리: tensorflow, pytorch, keras
텐서플로우
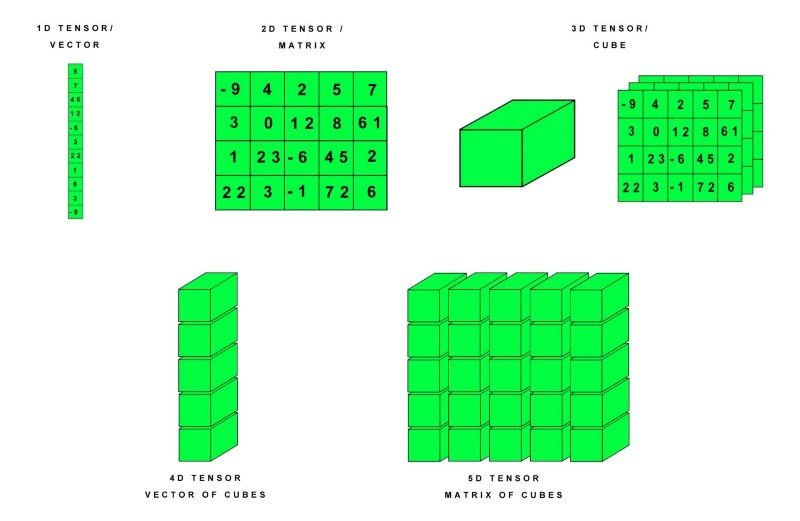
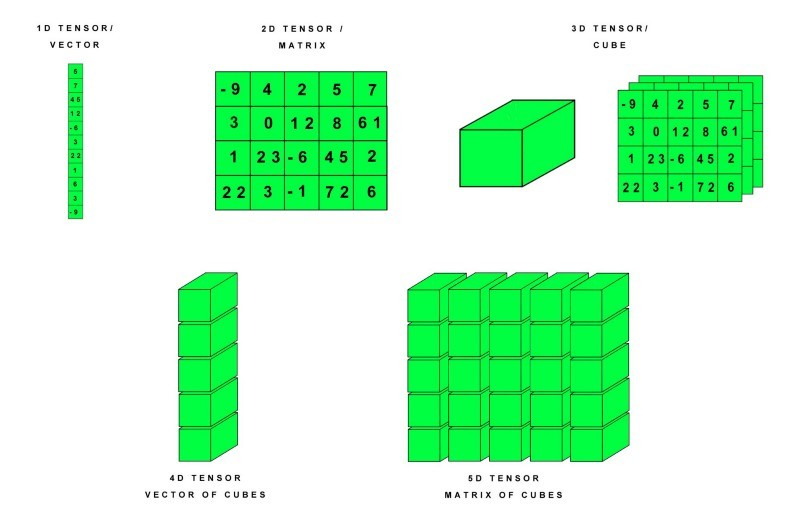
- Tensor란 많은 데이터를 효과적으로 처리하는 자료구조를 말하며 다차원 array, list라고 생각하면 편하다.
즉 모든 계산을 쉽게 하기 위해서 각각의 연산을 잘게 쪼개고 이것을 Graph로 연결한 것.
텐서플로: 퍼셉트론 학습
import tensorflow as tf
#OR 데이터 구축
x = [[0.0,0.0], [0.0,1.0], [1.0,0.0], [1.0,1.0]]
y = [[-1], [1], [1], [1]]
#퍼셉트론
w = tf.Variable(tf.random.uniform([2, 1], -0.5, 0.5))
b = tf.Variable(tf.zeros([1]))
# 옵티마이저
opt = tf.keras.optimizers.SGD(learning_rate=0.1)
#전방 계산 (식 (4.3))
def forward():
s = tf.add(tf.matmul(x, w), b)
o = tf.tanh(s) #하이퍼볼릭 탄젠트 활성화 함
return o
#손실 함수 정의
def loss():
o = forward()
return tf.reduce_mean((y-o)**2)
#500세대까지 학습 (100세대마다 학습 정보 출력)
for i in range(500):
opt.minimize(loss, var_list=[w, b])
if(i%100 ==0): print('loss at epoch', i, '=', loss().numpy())
#학습된 퍼셉트론으로 OR 데이터를 예측
o = forward()
print(o)출력결과:
loss at epoch 0 = 0.53569996
loss at epoch 100 = 0.08566681
loss at epoch 200 = 0.04078539
loss at epoch 300 = 0.025949078
loss at epoch 400 = 0.0188043
tf.Tensor(
[[-0.81756884][ 0.88712275]
[ 0.88711804][ 0.999282 ]], shape=(4, 1), dtype=float32)
tanh 함수는 입력값 x를 받아서 -1에서 1 사이의 값을 반환합니다. 함수의 그래프는 S자 형태를 가지며, x가 0에 가까울수록 값은 0에 가까워지고, x가 무한대로 갈수록 값은 -1 또는 1에 수렴합니다.
케라스 프로그래밍
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
#OR 데이터 구축
x = [[0.0,0.0], [0.0,1.0], [1.0,0.0], [1.0,1.0]]
y = [[-1], [1], [1], [1]]
n_input = 2
n_output = 1
perceptron = Sequential()
perceptron.add(Dense(units=n_output, activation='tanh',
input_shape = (n_input,),kernel_initializer='random_uniform',
bias_initializer='zeros'))
perceptron.compile(loss='mse', optimizer=SGD(learning_rate=0.1),
metrics=['mse'])
perceptron.fit(x, y, epochs=500, verbose=2)
res = perceptron.predict(x)
print(res)출력결과:
1/1 - 0s - loss: 0.0150 - mse: 0.0150 - 2ms/epoch - 2ms/step
Epoch 499/500
1/1 - 0s - loss: 0.0150 - mse: 0.0150 - 2ms/epoch - 2ms/step
Epoch 500/500
1/1 - 0s - loss: 0.0149 - mse: 0.0149 - 2ms/epoch - 2ms/step
1/1 [==============================] - 0s 53ms/step
[[-0.8162695 ][ 0.886334 ]
[ 0.88633883][ 0.9992656 ]]
텐서플로 프로그래밍: 다층 퍼셉트론으로 MNIST 인식
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
#MNUST 읽어 와서 신경망에 입력할 형태로 변환
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784) #텐서 모양 변환
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype(np.float32)/255.0 #ndarray로 변환
x_test = x_test.astype(np.float32)/255.0
y_train = tf.keras.utils.to_categorical(y_train, 10) #원핫 코드로 변환
y_test = tf.keras.utils.to_categorical(y_test, 10)
n_input=784
n_hidden=1024
n_output=10
mlp = Sequential()
mlp.add(Dense(units = n_hidden, activation='tanh', input_shape=(n_input,),
kernel_initializer='random_uniform', bias_initializer='zeros'))
mlp.add(Dense(units = n_output, activation='tanh',
kernel_initializer='random_uniform', bias_initializer='zeros'))
mlp.compile(loss='mean_squared_error', optimizer=Adam(learning_rate=0.001),
metrics=['accuracy'])
hist=mlp.fit(x_train, y_train, batch_size=128, epochs=30,
validation_data=(x_test, y_test), verbose=2)
res = mlp.evaluate(x_test, y_test, verbose=0)
print("정확률은", res[1]*100)
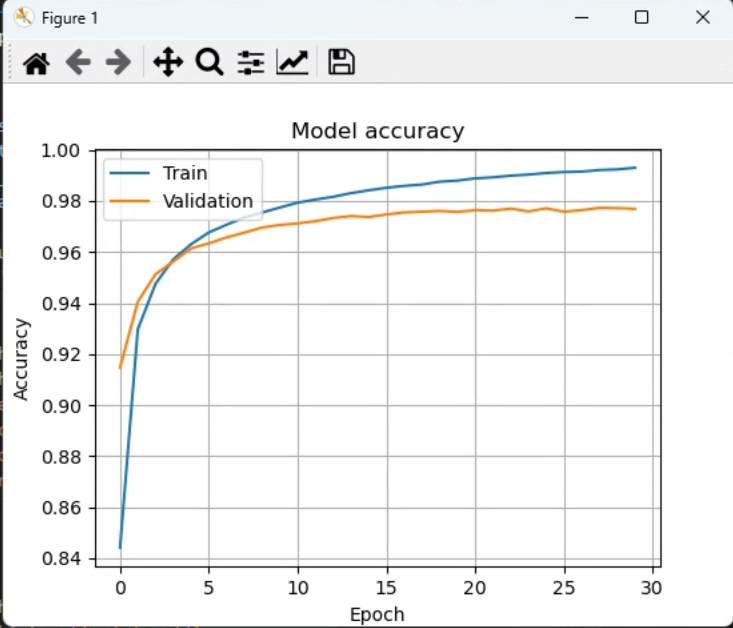
#정확률 곡선
plt.plot(hist.history['accuracy'])
plt.plot(hist.history['val_accuracy'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper left')
plt.grid()
plt.show()
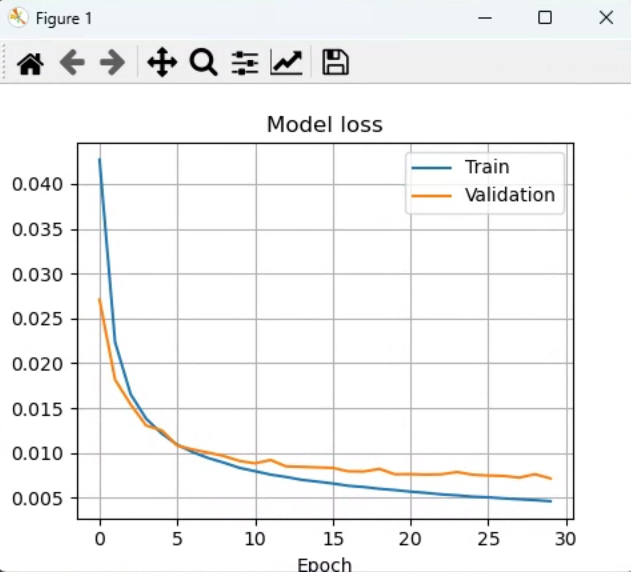
#손실 함수 곡선
plt.plot(hist.history['loss'])
plt.plot(hist.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper right')
plt.grid()
plt.show()출력결과:
Epoch 1/30
469/469 - 2s - loss: 0.0426 - accuracy: 0.8447 - val_loss: 0.0275 - val_accuracy: 0.9174 - 2s/epoch - 3ms/step
Epoch 2/30
469/469 - 1s - loss: 0.0224 - accuracy: 0.9295 - val_loss: 0.0179 - val_accuracy: 0.9430 - 1s/epoch - 3ms/step
…
Epoch 27/30
469/469 - 1s - loss: 0.0050 - accuracy: 0.9917 - val_loss: 0.0074 - val_accuracy: 0.9769 - 1s/epoch - 3ms/step
Epoch 28/30
469/469 - 1s - loss: 0.0048 - accuracy: 0.9919 - val_loss: 0.0075 - val_accuracy: 0.9776 - 1s/epoch - 3ms/step
Epoch 29/30
469/469 - 1s - loss: 0.0048 - accuracy: 0.9924 - val_loss: 0.0072 - val_accuracy: 0.9764 - 1s/epoch - 3ms/step
Epoch 30/30
469/469 - 1s - loss: 0.0047 - accuracy: 0.9929 - val_loss: 0.0076 - val_accuracy: 0.9777 - 1s/epoch - 3ms/step
정확률은 97.76999950408936
원핫 인코딩을 하는 이유: 데이터 분류하려고 사용
원핫 인코딩: 데이터를 차원이동 할 때 손실없이 하기 위해( 하나만 1이고 나머지 0)
깊은 다층 퍼셉트론
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from keras.datasets import fashion_mnist
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
#fashion MNIST 데이터셋을 읽어와 신경망에 입력할 형태로 변환
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
x_train = x_train.reshape(60000, 784) #텐서 모양 변환
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype(np.float32)/255.0 #ndarray로 변환
x_test = x_test.astype(np.float32)/255.0
y_train = tf.keras.utils.to_categorical(y_train, 10) #원핫 코드로 변환
y_test = tf.keras.utils.to_categorical(y_test, 10)
#신경망 구조 설정
n_input=784
n_hidden1=1024
n_hidden2=512
n_hidden3=512
n_hidden4=512
n_output=10
#신경망 구조 설계
mlp = Sequential()
mlp.add(Dense(units = n_hidden1, activation='tanh', input_shape=(n_input,),
kernel_initializer='random_uniform', bias_initializer='zeros'))
mlp.add(Dense(units = n_hidden2, activation='tanh',
kernel_initializer='random_uniform', bias_initializer='zeros'))
mlp.add(Dense(units = n_hidden3, activation='tanh',
kernel_initializer='random_uniform', bias_initializer='zeros'))
mlp.add(Dense(units = n_hidden4, activation='tanh',
kernel_initializer='random_uniform', bias_initializer='zeros'))
mlp.add(Dense(units = n_output, activation='tanh',
kernel_initializer='random_uniform', bias_initializer='zeros'))
#신경망 학습
mlp.compile(loss='mean_squared_error', optimizer=Adam(learning_rate=0.001),
metrics=['accuracy'])
hist=mlp.fit(x_train, y_train, batch_size=128, epochs=30,
validation_data=(x_test, y_test), verbose=2)
#신경망의 정확률 측정
res = mlp.evaluate(x_test, y_test, verbose=0)
print("정확률은", res[1]*100)
#정확률 곡선
plt.plot(hist.history['accuracy'])
plt.plot(hist.history['val_accuracy'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper left')
plt.grid()
plt.show()
#손실 함수 곡선
plt.plot(hist.history['loss'])
plt.plot(hist.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper right')
plt.grid()
plt.show()출력결과:
Epoch 1/30
469/469 - 4s - loss: 0.0350 - accuracy: 0.8099 - val_loss: 0.0269 - val_accuracy: 0.8348 - 4s/epoch - 9ms/step
Epoch 2/30
469/469 - 4s - loss: 0.0234 - accuracy: 0.8567 - val_loss: 0.0229 - val_accuracy: 0.8574 - 4s/epoch - 9ms/step
Epoch 3/30
469/469 - 4s - loss: 0.0210 - accuracy: 0.8687 - val_loss: 0.0223 - val_accuracy: 0.8533 - 4s/epoch - 9ms/step
…
Epoch 27/30
469/469 - 4s - loss: 0.0121 - accuracy: 0.9255 - val_loss: 0.0175 - val_accuracy: 0.8863 - 4s/epoch - 9ms/step
Epoch 28/30
469/469 - 4s - loss: 0.0121 - accuracy: 0.9261 - val_loss: 0.0180 - val_accuracy: 0.8864 - 4s/epoch - 9ms/step
Epoch 29/30
469/469 - 4s - loss: 0.0120 - accuracy: 0.9271 - val_loss: 0.0181 - val_accuracy: 0.8866 - 4s/epoch - 9ms/step
Epoch 30/30
469/469 - 4s - loss: 0.0117 - accuracy: 0.9290 - val_loss: 0.0178 - val_accuracy: 0.8860 - 4s/epoch - 9ms/step
정확률은 88.59999775886536
교차 엔트로피: 딥러닝이 사용하는 손실함수
- 엔트로피: 확률의 공정한 정도
ex) 찌그러진 주사위와 평범한 주사위 중 평범한 주사위의 엔트로피가 더 높음 - 교차 엔트로피: 두 확률 분포가 다른 정도
- 교차 엔트로피 손실 함수:
- 평균제곱오차와 교차 엔트로피 비교
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
#fashion MNIST 데이터셋을 읽어와 신경망에 입력할 형태로 변환
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784) #텐서 모양 변환
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype(np.float32)/255.0 #ndarray로 변환
x_test = x_test.astype(np.float32)/255.0
y_train = tf.keras.utils.to_categorical(y_train, 10) #원핫 코드로 변환
y_test = tf.keras.utils.to_categorical(y_test, 10)
#신경망 구조 설정
n_input=784
n_hidden1=1024
n_hidden2=512
n_hidden3=512
n_hidden4=512
n_output=10
#평균제곱오차를 사용한 모델
mlp_mse = Sequential()
mlp_mse.add(Dense(units = n_hidden1, activation='tanh', input_shape=(n_input,)))
mlp_mse.add(Dense(units = n_hidden2, activation='tanh'))
mlp_mse.add(Dense(units = n_hidden3, activation='tanh'))
mlp_mse.add(Dense(units = n_hidden4, activation='tanh'))
mlp_mse.add(Dense(units = n_output, activation='softmax'))
#신경망 학습
mlp_mse.compile(loss='mean_squared_error', optimizer=Adam(learning_rate=0.0001),metrics=['accuracy'])
hist_mse=mlp_mse.fit(x_train, y_train, batch_size=128, epochs=30, validation_data=(x_test, y_test), verbose=2)
#교차 엔트로피를 사용한 모델
mlp_ce = Sequential()
mlp_ce.add(Dense(units = n_hidden1, activation='tanh', input_shape=(n_input,)))
mlp_ce.add(Dense(units = n_hidden2, activation='tanh'))
mlp_ce.add(Dense(units = n_hidden3, activation='tanh'))
mlp_ce.add(Dense(units = n_hidden4, activation='tanh'))
mlp_ce.add(Dense(units = n_output, activation='softmax'))
#신경망 학습
mlp_ce.compile(loss='categorical_crossentropy', optimizer=Adam(learning_rate=0.0001),metrics=['accuracy'])
hist_ce=mlp_ce.fit(x_train, y_train, batch_size=128, epochs=30, validation_data=(x_test, y_test), verbose=2)
#두 모델 정확률 비교
res = mlp_mse.evaluate(x_test, y_test, verbose=0)
print("평균제곱오차의 정확률은", res[1]*100)
res = mlp_ce.evaluate(x_test, y_test, verbose=0)
print("교차 엔트로피의 정확률은", res[1]*100)
#정확률 곡선
plt.plot(hist_mse.history['accuracy'])
plt.plot(hist_mse.history['val_accuracy'])
plt.plot(hist_ce.history['accuracy'])
plt.plot(hist_ce.history['val_accuracy'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train_mse', 'Validation_mse', 'Train_cd', 'Validation_ce'], loc='upper left')
plt.grid()
plt.show()출력결과:
Epoch 25/30
469/469 - 4s - loss: 0.0036 - accuracy: 0.9991 - val_loss: 0.0946 - val_accuracy: 0.9765 - 4s/epoch - 9ms/step
Epoch 26/30
469/469 - 4s - loss: 0.0084 - accuracy: 0.9974 - val_loss: 0.0766 - val_accuracy: 0.9814 - 4s/epoch - 9ms/step
Epoch 27/30
469/469 - 4s - loss: 0.0018 - accuracy: 0.9997 - val_loss: 0.0658 - val_accuracy: 0.9829 - 4s/epoch - 9ms/step
Epoch 28/30
469/469 - 4s - loss: 8.4661e-04 - accuracy: 0.9999 - val_loss: 0.0648 - val_accuracy: 0.9839 - 4s/epoch - 9ms/step
Epoch 29/30
469/469 - 4s - loss: 0.0015 - accuracy: 0.9997 - val_loss: 0.0717 - val_accuracy: 0.9827 - 4s/epoch - 9ms/step
Epoch 30/30
469/469 - 4s - loss: 0.0110 - accuracy: 0.9967 - val_loss: 0.0816 - val_accuracy: 0.9808 - 4s/epoch - 9ms/step
평균제곱오차의 정확률은 98.01999926567078
교차 엔트로피의 정확률은 98.07999730110168
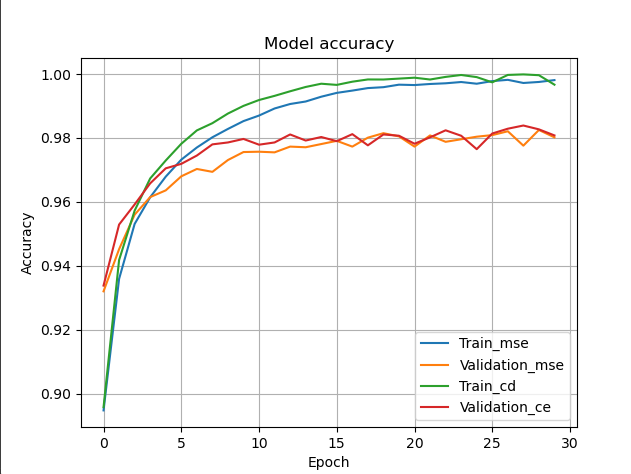
⇒교차 엔트로피의 정확률이 미세하게 우세하다는 걸 알 수 있다.
분류할 때 많이 사용
옵티마이저: 딥러닝이 사용하는 최적화 함수
모멘텀: 이전 운동량을 현재에 반영. 관성과 관련이 깊다. 이전 미니배치에서 얻었던 방향 정보를 같이 고려해 잡음을 줄이는 효과를 얻음
- Adagrad: 이전 그레이디언트 를 누적한 정보를 이용하여 학습률을 적응적으로 설정하는 기법
- RMSprop: 이전 그레이디언트를 누적할 때 오래된 것의 영향을 줄이는 정책을 사용하여 AdaGrad를 개선한 기법
- Adam: RMSprop에 모멘텀을 적용하여 RMSprop을 개선한 기법
옵티마이저의 성능 비교: SGD, Adam, Adagrad, RMSprop
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD, Adam, Adagrad, RMSprop
#fashion MNIST 데이터셋을 읽어와 신경망에 입력할 형태로 변환
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784) #텐서 모양 변환
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype(np.float32)/255.0 #ndarray로 변환
x_test = x_test.astype(np.float32)/255.0
y_train = tf.keras.utils.to_categorical(y_train, 10) #원핫 코드로 변환
y_test = tf.keras.utils.to_categorical(y_test, 10)
#신경망 구조 설정
n_input=784
n_hidden1=1024
n_hidden2=512
n_hidden3=512
n_hidden4=512
n_output=10
#하이퍼 매개변수 설정
batch_siz=256
n_epoch=50
#모델을 설계해주는 함수(모델을 나타내는 객체 model을 반환)
def build_model():
model = Sequential()
model.add(Dense(units = n_hidden1, activation='relu', input_shape=(n_input,)))
model.add(Dense(units = n_hidden2, activation='relu'))
model.add(Dense(units = n_hidden3, activation='relu'))
model.add(Dense(units = n_hidden4, activation='relu'))
model.add(Dense(units = n_output, activation='softmax'))
return model
#SGD 옵티마이저를 사용하는 모델
dmlp_sgd=build_model()
dmlp_sgd.compile(loss='categorical_crossentropy', optimizer=SGD(),metrics=['accuracy'])
hist_sgd=dmlp_sgd.fit(x_train, y_train, batch_size=batch_siz, epochs=n_epoch, validation_data=(x_test, y_test), verbose=2)
#Adam 옵티마이저를 사용하는 모델
dmlp_adam=build_model()
dmlp_adam.compile(loss='categorical_crossentropy', optimizer=Adam(),metrics=['accuracy'])
hist_adam=dmlp_adam.fit(x_train, y_train, batch_size=batch_siz, epochs=n_epoch, validation_data=(x_test, y_test), verbose=2)
#Adagrad 옵티마이저를 사용하는 모델
dmlp_adagrad=build_model()
dmlp_adagrad.compile(loss='categorical_crossentropy', optimizer=Adagrad(),metrics=['accuracy'])
hist_adagrad=dmlp_adagrad.fit(x_train, y_train, batch_size=batch_siz, epochs=n_epoch, validation_data=(x_test, y_test), verbose=2)
#RMSprop 옵티마이저를 사용하는 모델
dmlp_rmsprop=build_model()
dmlp_rmsprop.compile(loss='categorical_crossentropy', optimizer=RMSprop(),metrics=['accuracy'])
hist_rmsprop=dmlp_rmsprop.fit(x_train, y_train, batch_size=batch_siz, epochs=n_epoch, validation_data=(x_test, y_test), verbose=2)
#네 모델의 정확률을 출력
print("SGD의 정확률은", dmlp_sgd.evaluate(x_test,y_test,verbose=0)[1]*100)
print("Adam의 정확률은", dmlp_adam.evaluate(x_test,y_test,verbose=0)[1]*100)
print("Adagrad의 정확률은", dmlp_adagrad.evaluate(x_test,y_test,verbose=0)[1]*100)
print("RMSprop의 정확률은", dmlp_rmsprop.evaluate(x_test,y_test,verbose=0)[1]*100)
#네 모델의 정확률을 하나의 그래프에서 비교
plt.plot(hist_sgd.history['accuracy'], 'r')
plt.plot(hist_sgd.history['val_accuracy'], 'r--')
plt.plot(hist_adam.history['accuracy'], 'g')
plt.plot(hist_adam.history['val_accuracy'], 'g--')
plt.plot(hist_adagrad.history['accuracy'], 'b')
plt.plot(hist_adagrad.history['val_accuracy'], 'b--')
plt.plot(hist_rmsprop.history['accuracy'], 'm')
plt.plot(hist_rmsprop.history['val_accuracy'], 'm--')
plt.title('Model accuracy')
plt.ylim(0.6, 1.0)
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train_sgd', 'Validation_sgd', 'Train_adam', 'Validation_adam', 'Train_adagrad', 'Validation_adagrad', 'Train_rmsprop', 'Validation_rmsprop'], loc='best')
plt.grid()
plt.show()출력결과:
Epoch 44/50
235/235 - 4s - loss: 0.0098 - accuracy: 0.9986 - val_loss: 0.2764 - val_accuracy: 0.9844 - 4s/epoch - 15ms/step
Epoch 45/50
235/235 - 4s - loss: 0.0094 - accuracy: 0.9983 - val_loss: 0.2841 - val_accuracy: 0.9815 - 4s/epoch - 16ms/step
Epoch 46/50
235/235 - 4s - loss: 0.0079 - accuracy: 0.9985 - val_loss: 0.2985 - val_accuracy: 0.9847 - 4s/epoch - 16ms/step
Epoch 47/50
235/235 - 4s - loss: 0.0085 - accuracy: 0.9987 - val_loss: 0.3409 - val_accuracy: 0.9836 - 4s/epoch - 16ms/step
Epoch 48/50
235/235 - 4s - loss: 0.0086 - accuracy: 0.9988 - val_loss: 0.2713 - val_accuracy: 0.9817 - 4s/epoch - 15ms/step
Epoch 49/50
235/235 - 4s - loss: 0.0135 - accuracy: 0.9980 - val_loss: 0.3732 - val_accuracy: 0.9789 - 4s/epoch - 16ms/step
Epoch 50/50
235/235 - 4s - loss: 0.0099 - accuracy: 0.9986 - val_loss: 0.3639 - val_accuracy: 0.9838 - 4s/epoch - 16ms/step
SGD의 정확률은 97.39000201225281
Adam의 정확률은 98.580002784729
Adagrad의 정확률은 95.01000046730042
RMSprop의 정확률은 98.37999939918518
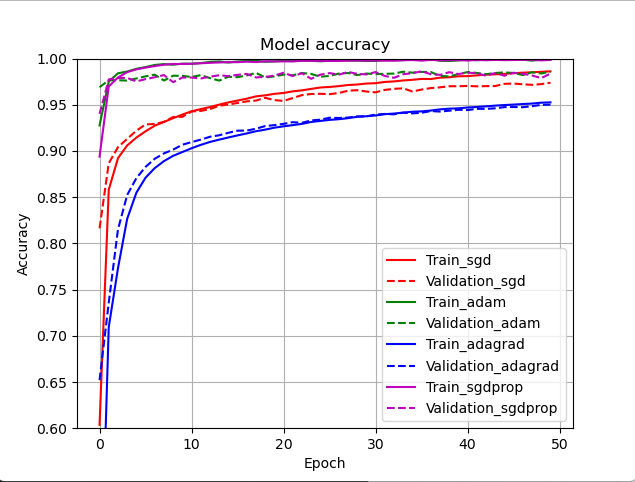
⇒Adam과 RMSprop이 경합을 이룸
⇒다시 실행시 결과가 달라질수 있음