바닥부터 배우는 강화학습4 알파고와 MCTS(2)

MCTS(Monte Calro Tree Search)

• 주어진 상황에 특화된 해를 찾는데 쓰이는 플래닝 알고리즘
• 그 상황에서만 사용할 수 있기 때문에 보편적 상황에서는 성능이 떨어짐.
• 다양한 액션을 취해보고 가장 좋았던 결과의 액션을 채택.
• “그냥 많이 둬 보는” 방법론

MCTS의 사용 조건

1. MDP 사용
   1. 상태 전이 확률
   2. 보상 함수
   3. MDP로 시뮬레이션
2. 시간적 틈
   1. 액션 사이의 시간적 여유 필요 (MCTS 실행되는 시간)

알파고에서의 MCTS

1. 선택
2. 확정
3. 시뮬레이션
4. 백 프로파게이션

• 1~4 돌면 트리에 새로운 ‘노드’ 하나 생성
• ‘노드’ = 바둑판의 한 상태 s
• ‘노드’에서 뻗어나가는 ‘엣지’ = 액션 a
• 과정 반복하여 노드 추가하는 과정

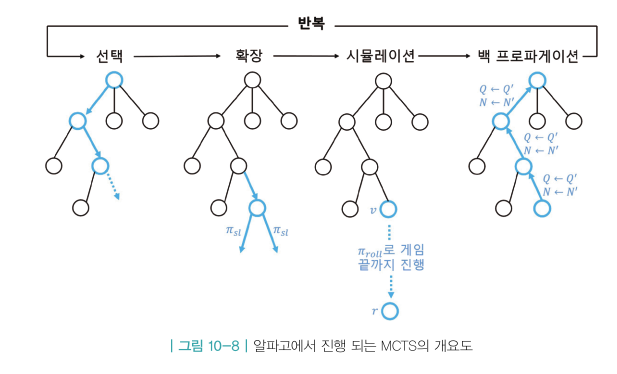
1.선택

• 루트 노드에서 출발하여 리프 노드까지 가는 과정

• $Q(s_t,a)$ : 시뮬레이션 실행 후 얼마나 좋은지
• $u(s_t,a)$ : 시뮬레이션 실행 전에 얼마나 좋을 것이라 추측하는지 ⇒ 시뮬레이션이 진행될 수록 Q는 커지고 u는 작아진다.
  

Q(s, a)

• $Q(s,a)$ : s 에서 a 를 하는 것의 밸류, s 에서 a를 선택한 이후 도달한 리프 노드들의 평균을 통해 계산
• $s_L^i$ : 리프노드
• 어떤 상태s(78)에서 액션a(33)를 선택하는 경험들을 100번 지나서 도달한 리프 노드의 평균 밸류

u(s, a)

• $P(s, a)$ : 사전 확률로, 시뮬레이션 해보기 전에 각 액션에 확률을 부여
• 휴먼 데이터를 사용했던 지도학습 정책을 사용
• $P(s,a) = \pi_{sl}(s,a)$
• $N(s,a)$ : 시뮬레이션 도중 엣지(s, a) 를 지나간 수
• $N(s, a) = 0$ 에서 시작하여 한 번 지나갈 때마다 1씩 더해짐
• N 값이 커질수록 휴먼데이터 영향력 감소 ⇒ 컴퓨터가 학습한 데이터 영향력 증가

2. 확장

• 방금 도달한 리프 노드를 실제로 트리에 매달아주는 과정
• 엣지들의 다양한 정보를 초기화

• Q + u 값 계산 가능
• 리프 노드에서 액션을 선택할 수 있게 되므로 더 이상 리프 노드가 아님
• 리프 노드를 실제 트리의 노드로 확장한 것

3. 시뮬레이션

• 리프 노드가 트리의 정식 노드가 되어서 이 노드의 가치를 평가해주어야 함
• 평가 방법

  1. 시뮬레이션

     • 리프 노드부터 게임이 끝날 때까지 빠르게 시뮬레이션
     • 롤아웃 정책 이용 (실력 떨어지나 빠른 연산 가능한 뉴럴넷)
     • 시뮬레이션 결과 값을 밸류로 활용

  2. 밸류 네트워크 활용
     - 상태 s부터 강화학습 정책으로 플레이 했을 때 누가 이길지 예측 해주는 함수
     - 이 함수에 리프 노드를 인풋으로 넣어주면 밸류 바로 알 수 있음

     ⇒알파고에서 이 둘을 반반 섞어서 사용

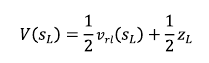
4. 백 프로파게이션

• Q(s,a) : 해당 엣지를 지나서 도달한 리프 노드 밸류의 평균
• 위 평균 값을 계산 해주는 게 백 프로파게이션

⇒ 새로운 리프노드가 생길 때마다 평균값을 업데이트해주는 것.

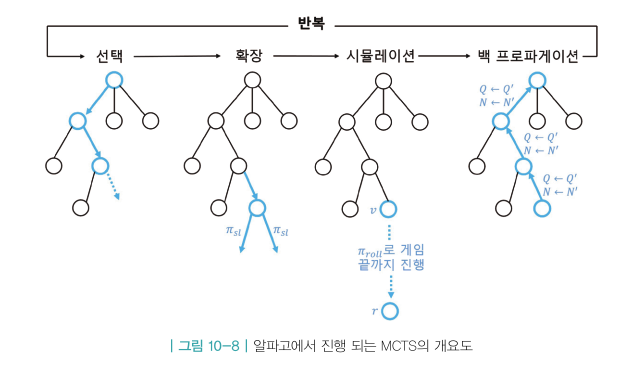
• 모든 엣지의 Q, N 값을 업데이트

• 지나온 모든 엣지에 대해 카운터의 값은 1 증가
• Q 값은 V 의 방향으로 조금 업데이트
• 리프의 평가를 진행. (리프 노드 → 루트 노드 방향으로 역전파)

⇒이렇게 하나의 노드가 새롭게 탄생

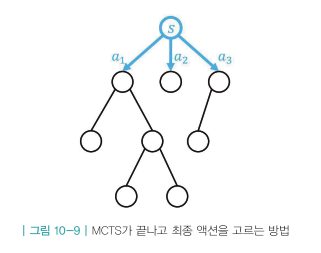
• s에서 a 선택 할 때 액션 밸류인 Q가 높은 걸 선택하는게 아닌 방문 횟수N가 가장 큰 액션 선택 ⇒a1 선택
  • 방문 횟수가 많을 수록 u의 영향력 감소, Q의 영향력 증가
  • Q가 크다는 것은 그 엣지를 지나서 도달했던 리프 노드의 가치가 높았다는 뜻 ⇒결국 방문 횟수N를 선택하는 게 가치가 높은 액션을 선택하는 합리적인 길 ⇒바로 Q밸류가 높은 걸 선택하지 않는 이유는 신뢰도 고려 ex)음식점 별점