[자료구조] Heap Sort 힙정렬

합병 정렬의 문제점

정렬한 레코드 수에 비례하여 저장 공간이 추가로 필요하다

히프 정렬 heap sort

• 일정한 양의 저장 공간만 추가로 필요하다 (조금만 더 있으면 된다)

• 최악의 경우 연산 시간과 평균 연산 시간 : O(nlogn)
  ⇒ O(n)의 추가 저장 공간을 사용하는 합병 정렬보다는 약간 느리지만 O(1)의 추가 저장공간을 사용하느 합병 정렬보다는 빠르다

• 최대-히프 구조 사용
  : 최대-히프와 연관된 삭제, 삽입 함수 → O(nlogn) 정렬 방법
  : adjust 함수 사용 → 최대 히프를 재조정
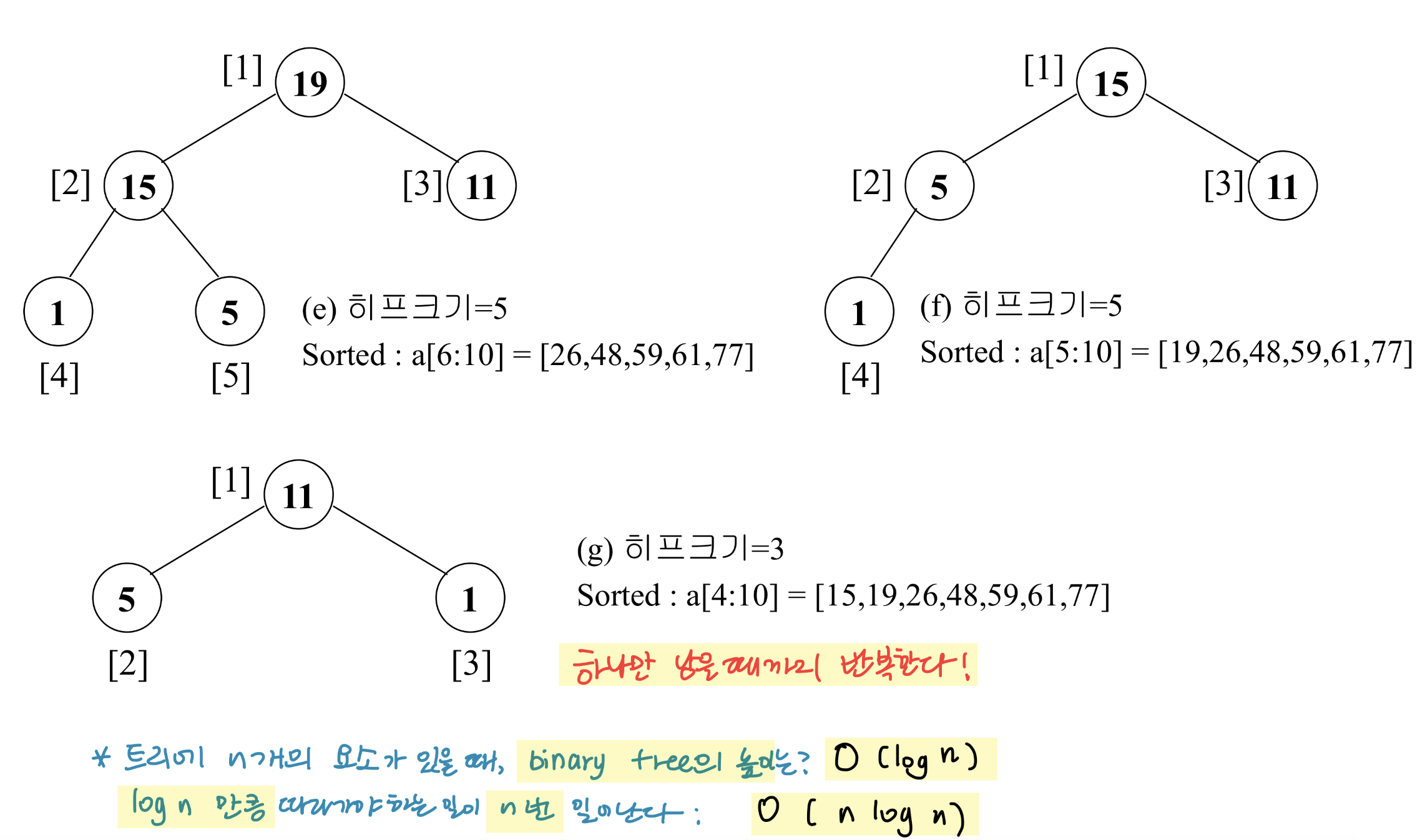
  : 최대 히프 구조를 이용해서 root 에 가장 큰 숫자 올린 다음 (최대 히프 구조로 만든 다음) 가장 아래로 뽑아서 배열에 저장한다.

• 이진트리로 변환된 배열 입력리스트 : (26, 5, 77, 1, 61, 11, 59, 15, 48, 19)
  
  
  

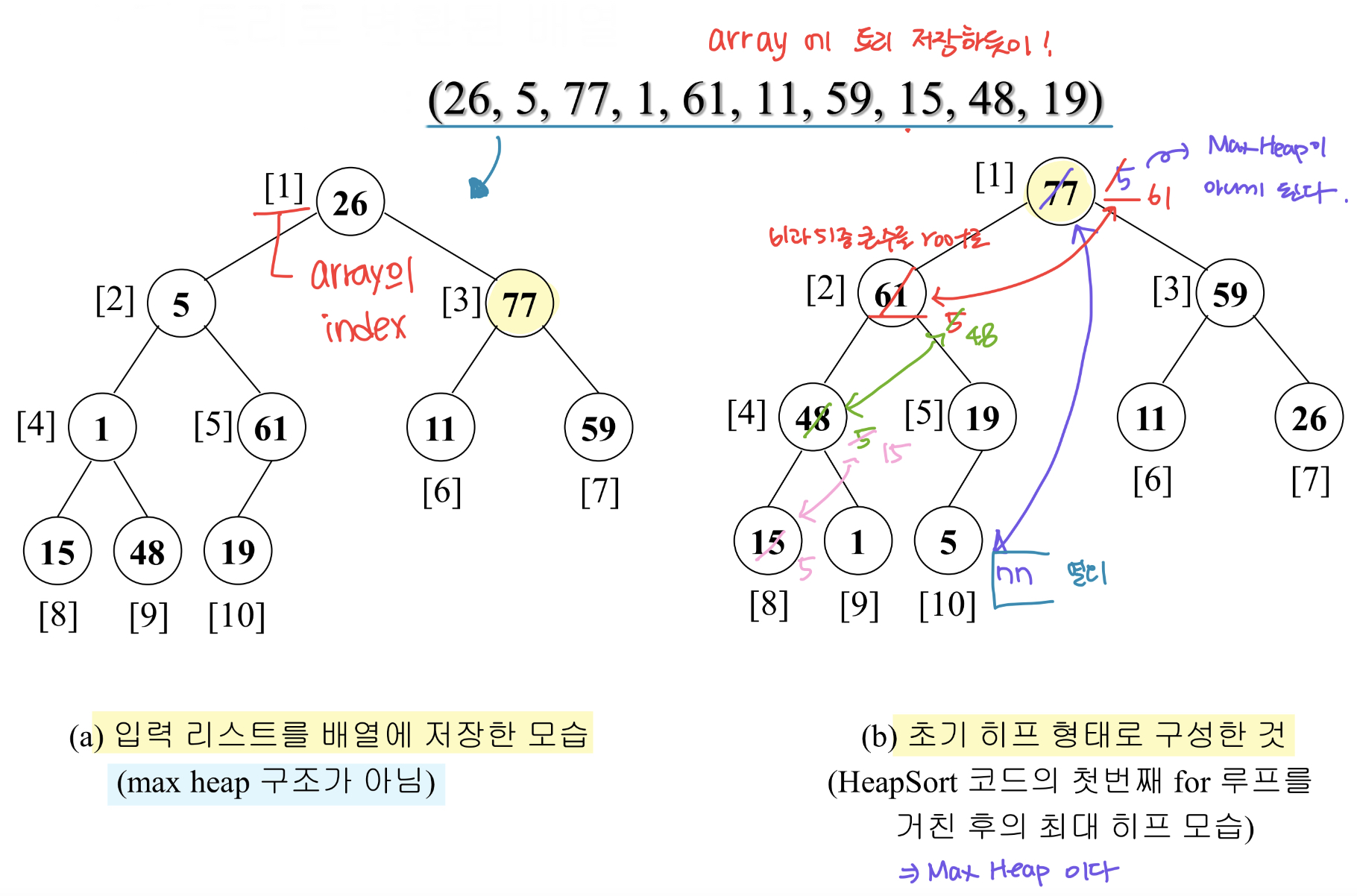
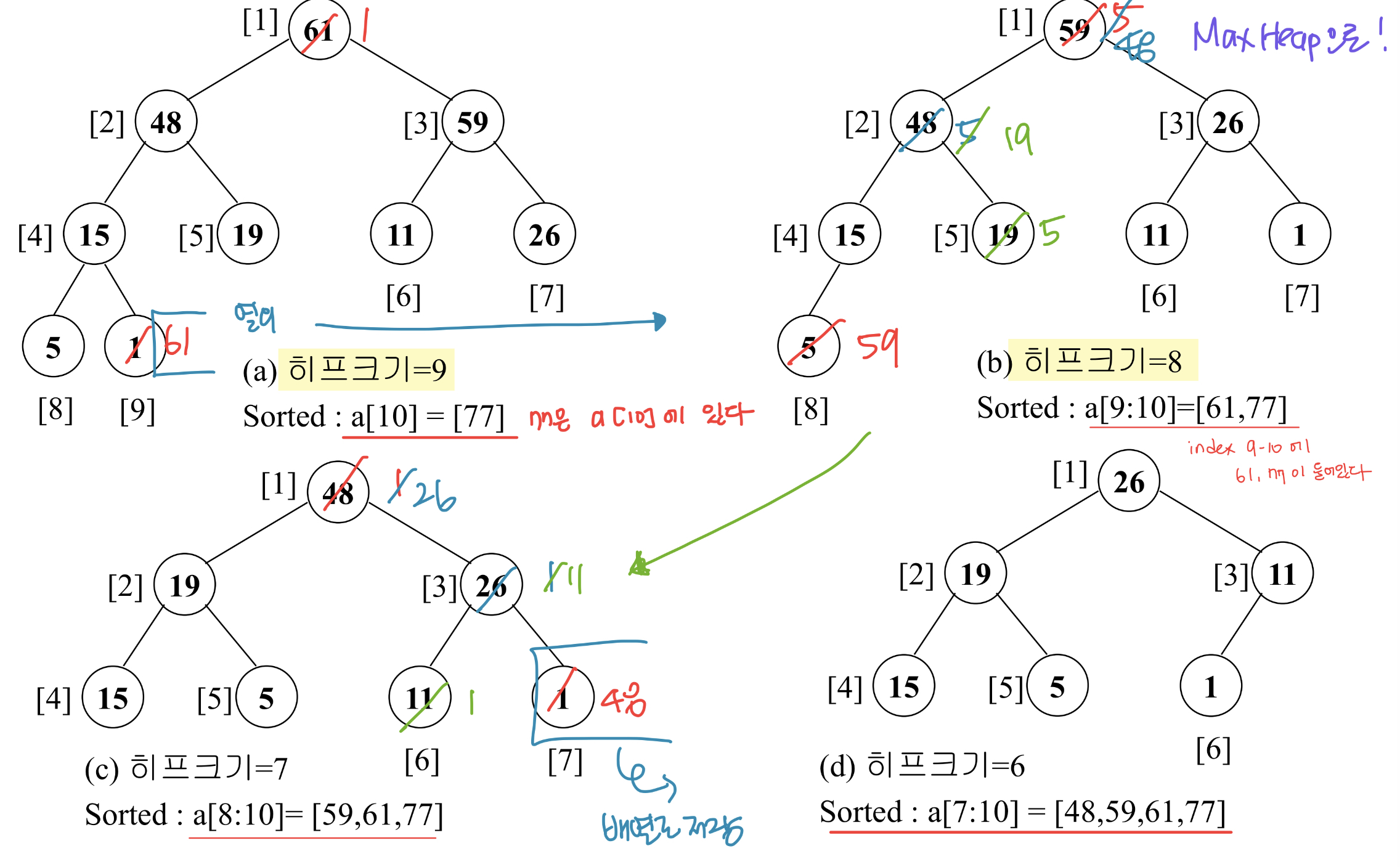
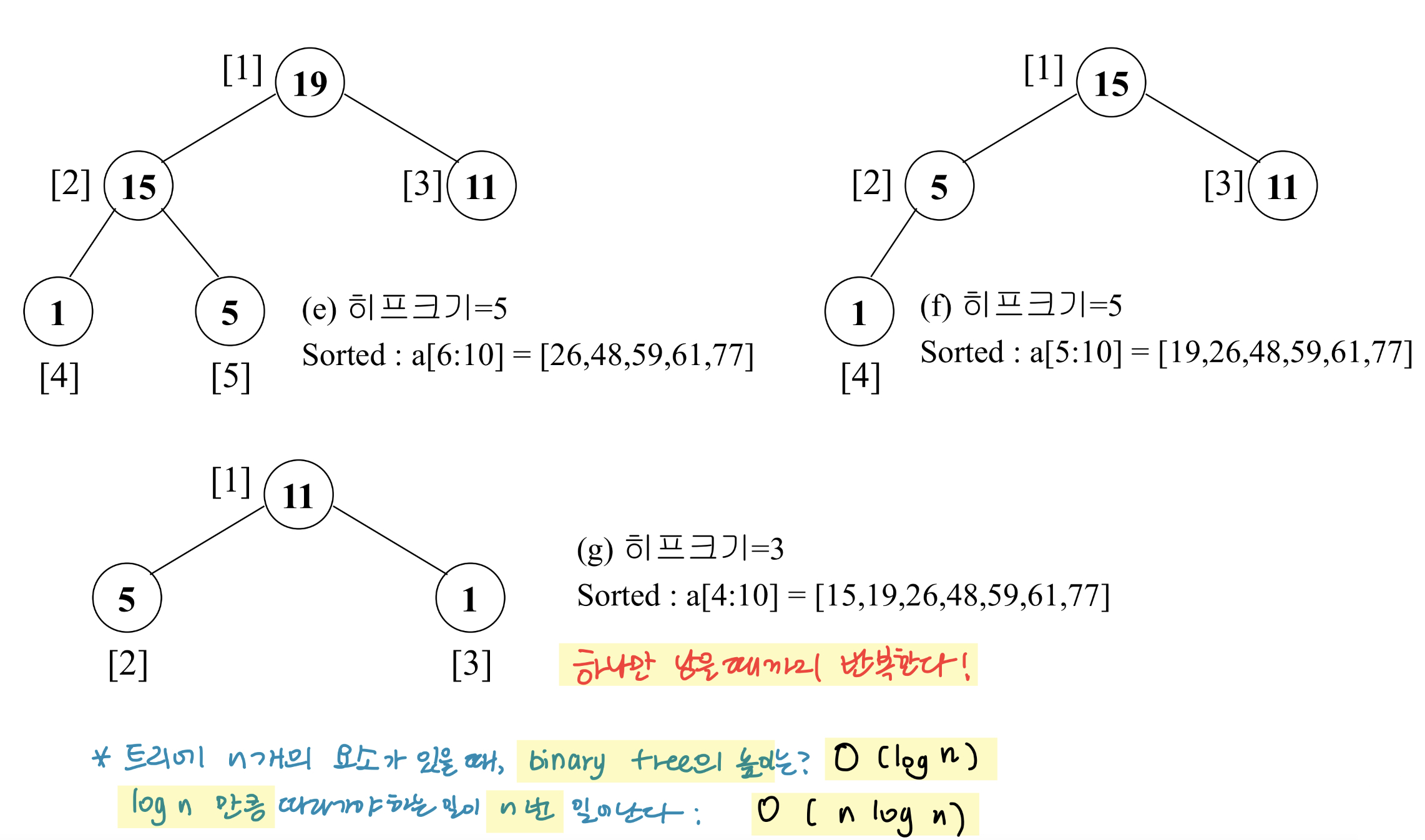
Adjust 함수

• 왼쪽 및 오른쪽 서브 트리가 모두 히프인 이진 트리에서 시작해 이진 트리 전체가 최대 히프가 되도록 재조정
• 연산 시간 : O(d) (d는 트리의 깊이)
  

    // Max Heap 만드는 함수
    template<class T>
    void Adjust(T* a, const int root, const int n){ // root 와 n개를 가지고 시작한다
        
        //루트 root를 가진 이지트리를 히프 성질을 만족하도록 조정한다
        // root의 왼쪽과 오른쪽 서브 트리는 현재도 히프 성질 만족함
        // 어떤 노드도 n보다 큰 인덱스 가지지 않는다.
        
        T e = a[root]; // 루트에 있는 걸 가져다가 e에 대한 적절한 위치를 탐색한다.
        
        int j;
         // 곱하기 2한게 자식이지.
        for (j = 2*root; j<=n; j*=2){ //
            if(j<n && a[j] < a[j+1]) // j는 parent의 가장 큰 노드
                j++;
            
            if (e >= a[j]) // e는 j의 parent로 삽입
                break;
            
            a[j/2] = a[j]; 
            // 그 위치로 제일 작은걸 내려보낸다 (j번째 레코드를 트리 위로 이동시킨다)
        }
        
        a[j/2] =e;
    }

    template<class T>
    void HeapSort(T* a, const int n){
        for (int i = n/2, i >= 1; i--) // 히프로 바뀐다.
            // 부모~root까지 가면서 계속 Adjust
            Adjust(a, i, n);
        
        for (int i = n-1; i>=1; i--){ // 정렬
            swap(a[1], a[i+1]); // 현 히프의 처음과 마지막 교환
            Adjust(a, 1, i); // 조정
        }
    }

정렬과정

Adjust를 반복적으로 호출 → 최대 히프 구조 만든다