합병정렬
- 두 개의 정렬된 리스트를 하나의 정렬된 리스트로 합병
template<class T>
void Merge(T* initList, T* mergeList, const int l, const int m, const int n){
// initList[l:m]과 initList[m+1:n]이 들어와서
// mergedList[l:n] 으로 합병될 것이다!!
int i1, iResult, i2;
for (i1 = 1, iResult = 1, i2 = m+1;
// 시~작! 하나는 1부터 시작, 하나는 m+1부터 시작한다
i1<= m && i2<=n;
iResult++)
if (initList[i1] <= initList[i2]){
// 작은 것 먼저 합병 시킬 것이다
mergeList[iResult] = initList[i1]];
i1++; // i1이 작으면 i1 증가
}
else { // 반대인 경우
mergeList[iResult] = initList[i2]; // i2 합병시켜라
i2++; // i2 증가시켜라
}
// 남는 경우가 있으면 남은 것 다 복사한다.
copy (initList + i1, initList + m + 1, mergedList + iResult);
// 첫번째 리스트의 나머지 레코드가 있다면 복사한다
copy (initList + i2, initList + n + 1, mergedList + iResult);
// 두번째 리스트의 나머지 레코드 있다면 복사한다
}
// 합병하는데 걸리는 시간 복잡도 : 리스트의 길이와 같다 - 합병 시간 : O(n-l+1)
⇒ 합병될 레코드 수와 동일하다.
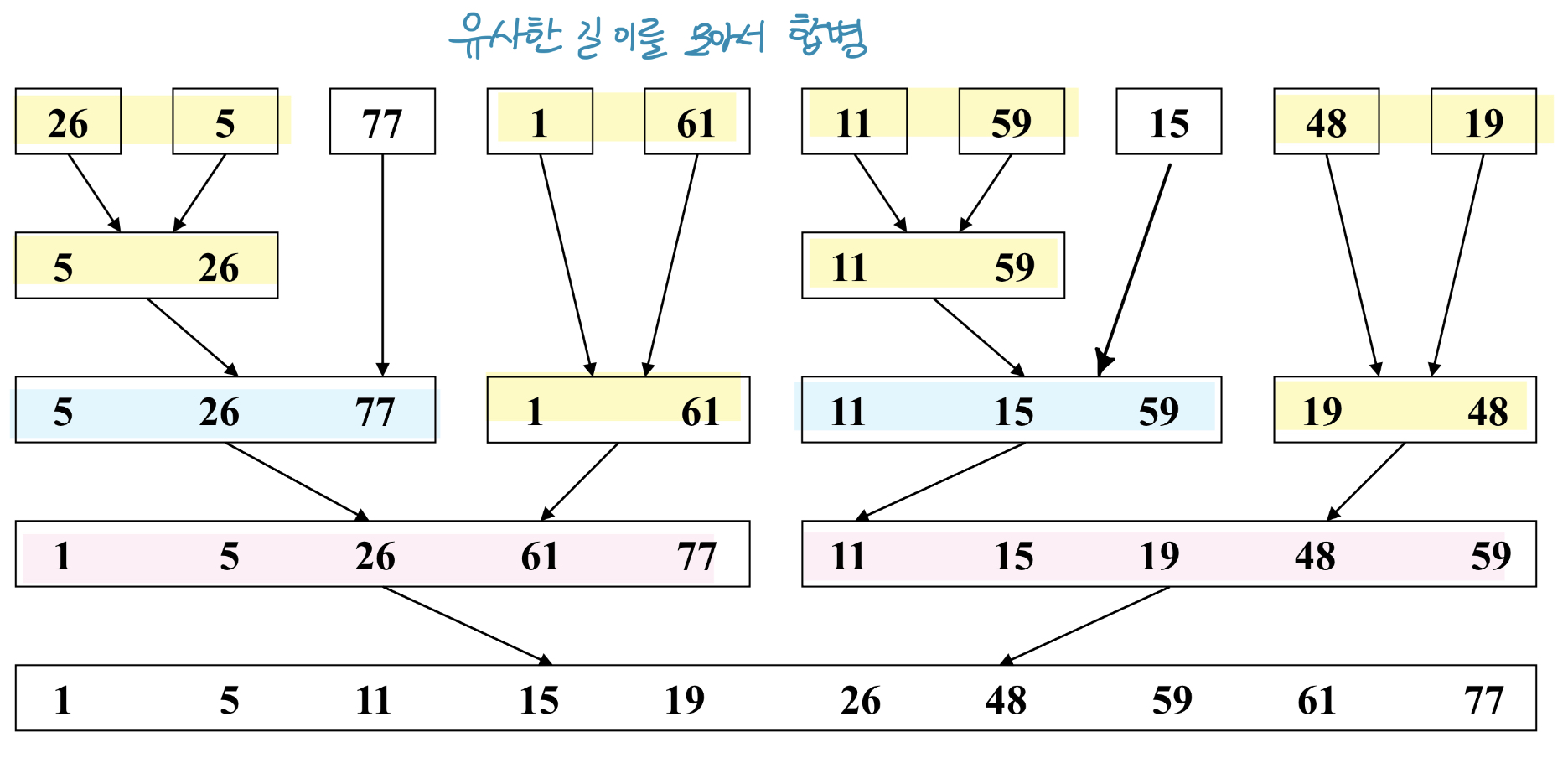
반복 합병 정렬 Iterative Merge Sort
입력 리스트를 길이가 1인 n개의 정렬된 서브리스트로 간주
반복 합병 정렬의 단계
- 첫 번째 합병 단계
: 리스트들을 쌍으로 합병하여 크기가 2인 n/2 개의 리스트를 얻는다.
→ n이 홀수이면 리스트 하나는 크기가 1
- 두 번째 합병 단계
: n/2 개의 리스트를 다시 쌍으로 합병하여 n/4개의 리스트를 얻는다 - 합병 단계는 서브리스트가 단 하나 남을 때 까지 계속된다
→ 한번 합병할 때마다 서브 리스트의 수는 반으로 줄어든다.
반복 정렬의 시간 복잡도
O (n log n)
한 번 쭉 스캔할 때 n번 합병 해야 한다 → 이 합병을 log n번 해야 하기 때문에 총 시간 복잡도는 O(nlogn)
template<class T>
void MergePass(T* initList, T* resultList, const int n, const int s){
int i;
for (i = 1; // 1부터 시작해서
i < n - 2*s + 1; // 여기까지
i += 2*s) // 길이를 두 배씩 늘리며 간다
Merge(initList, resultList, i, i+s-1, i + 2*s - 1);
// initList를 줄테니 result를 받아와라. 길이를 두 배로 늘리며 받아와라 !
// 2*s 보다 작은 수의 원소가 남은 경우
if ((i+s-1) < n) // 남아있는 수를 합병해라
Merge(initList, resultList, i, i+s-1, n);
else // 남아있는게 없으면 결과에 Copy하고 끝!
copy(initList + i, initList + n + 1, resultList + i);
}template<class T>
void MergeSort(T *a, const int n){ // 원래 리스트는 a
T *tempList = new T[n+1];
// 추가 메모리가 필요하다 -> 이것은 레코드의 크기와 비례한다
for (int l = 1; l < n; l *= 2){
// l은 현재 합병되고 있는 서브리스트의 길이
MergePass(a, tempList, n, l);
l *= 2;
MergePass(tempList, a, n, l);
}
delete [] tempList;
}- MergeSort 분석
- i번째 패스 : 크기가 인 리스트를 합병
- 총 단계가 데이터에 적용된다.
- 합병의 각 단계에 걸리는 시간 : O(n)
- 총 연산 시간 : O (n log n)
순환 합병 정렬 Recursive Merge Sort
- 정렬할 리스트를 거의 똑같이 두 개로 나눈다 ⇒ Left 서브리스트와 right 서브리스트로
- 서브리스트들은 순환적으로 정렬된다
- 정렬된 서브리스트들은 합병된다
순환적 합병 정렬의 서브 리스트 분할
-
두 개의 서브리스트를 만든다
left ~ (left + right) / 2 , (left + right) / 2 + 1 ~ right -
정수 배열 link [l:n] 사용
- 함수 Merge 가 사용될 때 일어나는 레코드 복사를 제거하기 위해 정수 포인터를 각 레코드에 연관 시키기 위한 것
- list[i] : 정렬된 서브리스트에서 레코드 i 다음에 있는 레코드
- 레코드 복사하기 싫다!! (비용 너무 많이 드므로) 링크 변경으로 대체되고 정렬 함수의 실행 시간은 레코드 크기 s에 독립적이 된다
- 필요한 추가 공간 : O(n)
- 최종 체인이 결정하는 정렬 순서로 레코드들을 물리적으로 재정돈 해야 하는 후처리 필요함
순환 합병 정렬 (Recursive Merge Sort) 구현
template<class T>
int rMergeSort(T* a, int* link, const int left, const int right){
// a는 레코드의 집합 (키의 집합),
if (left<=right)
return left;
int mid = (left + right) / 2; // mid값 정해주고
return ListMerge(a, link, rMergeSort(a, link, left, mid),
// 왼쪽 반 정렬
rMergeSort(a, link, mid + 1, right);
// 오른쪽 반 정렬
}rMergeSort분석- 합병 정렬의 순환 버전
- 안정적이다
- 연산시간 : O(nlogn)
합병 정렬의 변형
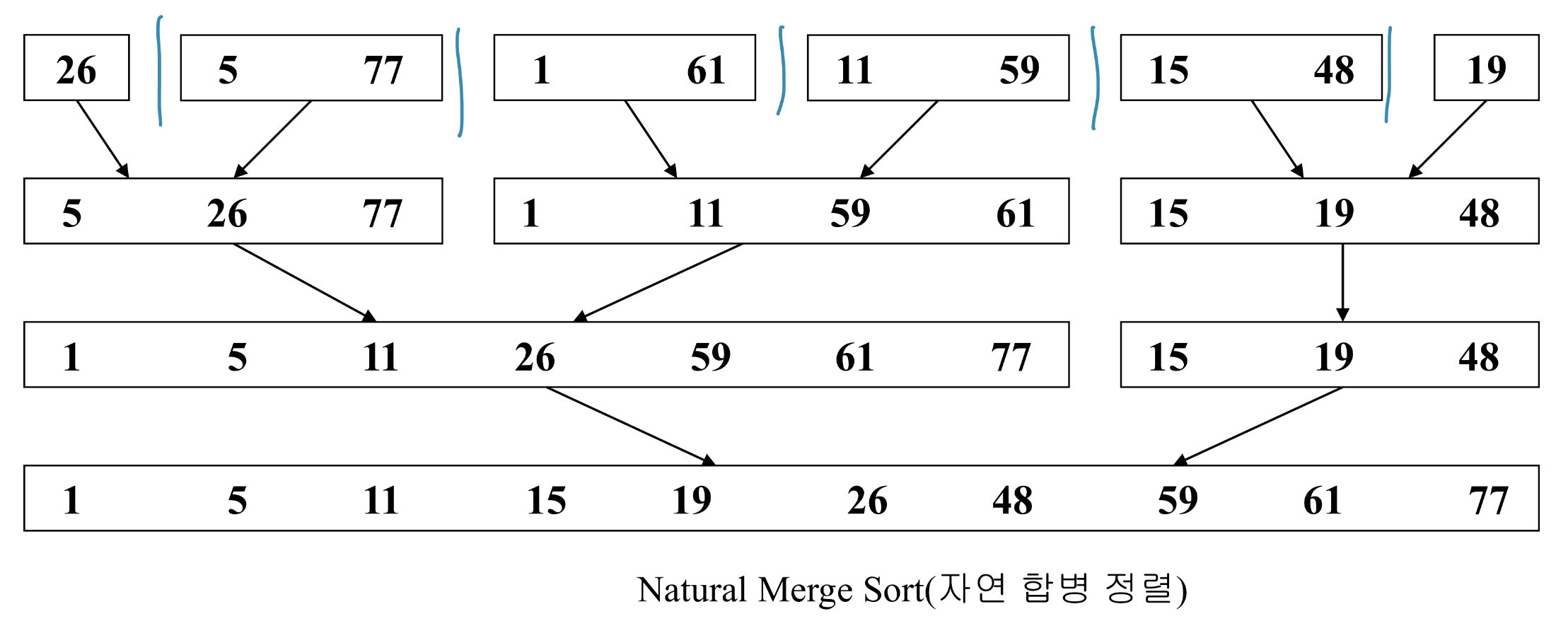
자연 합병 정렬 Natural Merge Sort
입력 리스트 내에 이미 존재하고 있는 순서를 고려해서 자른 다음 recursive merge sort나 iterative merge sort를 실시하면 된다
참고 교재 : C++자료구조론
