[알고리즘] Graph Coloring

💫 Graph Coloring

지도에 m가지 색을 가지고 색칠하는 문제.
m개의 색을 가지고 인접한 지역이 같은 색이 되지 않도록 지도에 색칠해야 한다.

📁 유망한 노드인지 판단여부

• 상태 이상 트리에서 기준이 되는 노드의 부모노드, 자식노드가 기준이 되는 노드와 같은지 판단한다.
  • 인접한 노드들과 색이 같다 ⇒ 유망하지 않다.
  • 인접한 노드들과 색이 같지 않다. ⇒ 유망하다.

📁 Graph Coloring ****

void m_coloring (index i) {
    int color;
    // 현재 노드 i에서 유망한지 확인
    if (promising(i)) {
        // 만약 i가 마지막 정점이라면 (모든 정점이 색칠 완료된 상태)
        if (i == n) 
            // vcolor 배열에 저장된 각 정점의 색상을 출력
            cout << vcolor[1] through vcolor[n];
        else
            // 각 색상 (1부터 m까지)을 정점 i+1에 시도
            for (color = 1; color <= m; color++) {
                vcolor[i+1] = color; // 정점 i+1에 현재 색상 할당
                m_coloring(i+1); // 다음 정점으로 재귀 호출
            }
    }
}

bool promising(index i) {
    int j;
    bool switch;
    switch = TRUE; // 초기 상태에서 유망하다고 가정
    j = 1;

    // 현재 노드와 이전 노드 간 색상 충돌 여부를 확인
    while (j < i && switch) {
        // 두 정점이 연결되어 있고, 색상이 같다면 유망하지 않음
        if (W[i][j] && vcolor[i] == vcolor[j]) 
            switch = FALSE;
        j++;
    }

    // 유망 여부 반환 (TRUE: 유망, FALSE: 유망하지 않음)
    return switch;
}

• 알고리즘 적용

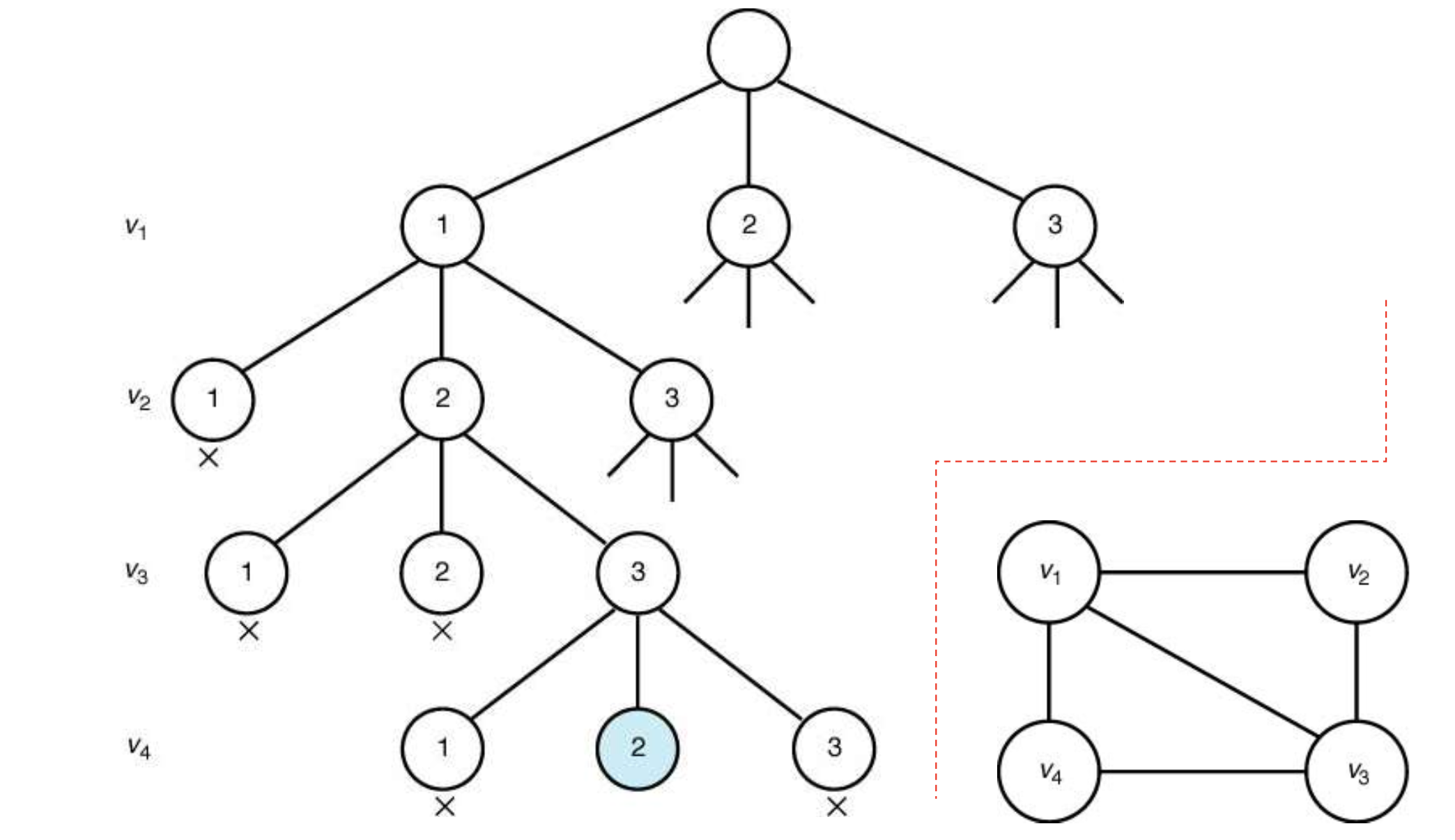
📁 시간 복잡도

시간복잡도 : $2^n$