[알고리즘] Sum-of-subsets Problem

💫 Sum-of-subsets Problem

주어진 정수 집합과 목표 합계를 기반으로, 집합의 부분 집합 중에서 원소들의 합이 주어진 목표 값과 일치하는 경우를 찾는 문제

📁 유망한 노드인지 판단여부

조건 - 가중치를 오름차순으로 정렬한 경우, 노드가 유망하지 않음을 판단

1. 현재까지 선택한 가중치의 합 (weight)

   weight : 현재 노드의 레벨 까지 포함된 가중치의 합.

   상황 :   $weight + w_{i+1} > W$ 

   → 현재까지의 가중치 합 에 다음 가중치 를 추가했을 때, 목표값 를 초과하면 유망하지 않은 노드로 간주

2. 남은 모든 가중치의 총합 (total)

   $total$ : 아직 선택되지 않은 남은 가중치들의 합.

   상황 :   $weight + total < W$ 

   → 현재까지의 가중치 합 와 남은 모든 가중치의 합 을 더해도 목표값 에 도달할 수 없다면, 유망하지 않은 노드로 간주

📁  Sum-of-subsets Problem

void sum_of_subsets (index i, int weight, int total) {
   if (promising(i)) {
      if (weight ==W)
          cout << include[1] through include[i];
      else {
          include[i+1] = “yes”;
          sum_of_subsets(i+1, weight+w[i+1], total-w[i+1]);
          include[i+1] = “no”;
          sum_of_subsets(i+1, weight, total-w[i+1]);
   } 
}

bool promising (index i) {
   return (weight+total >= W)
   	    && (weight == W || weight+w[i+1] <= W);
}

• Example

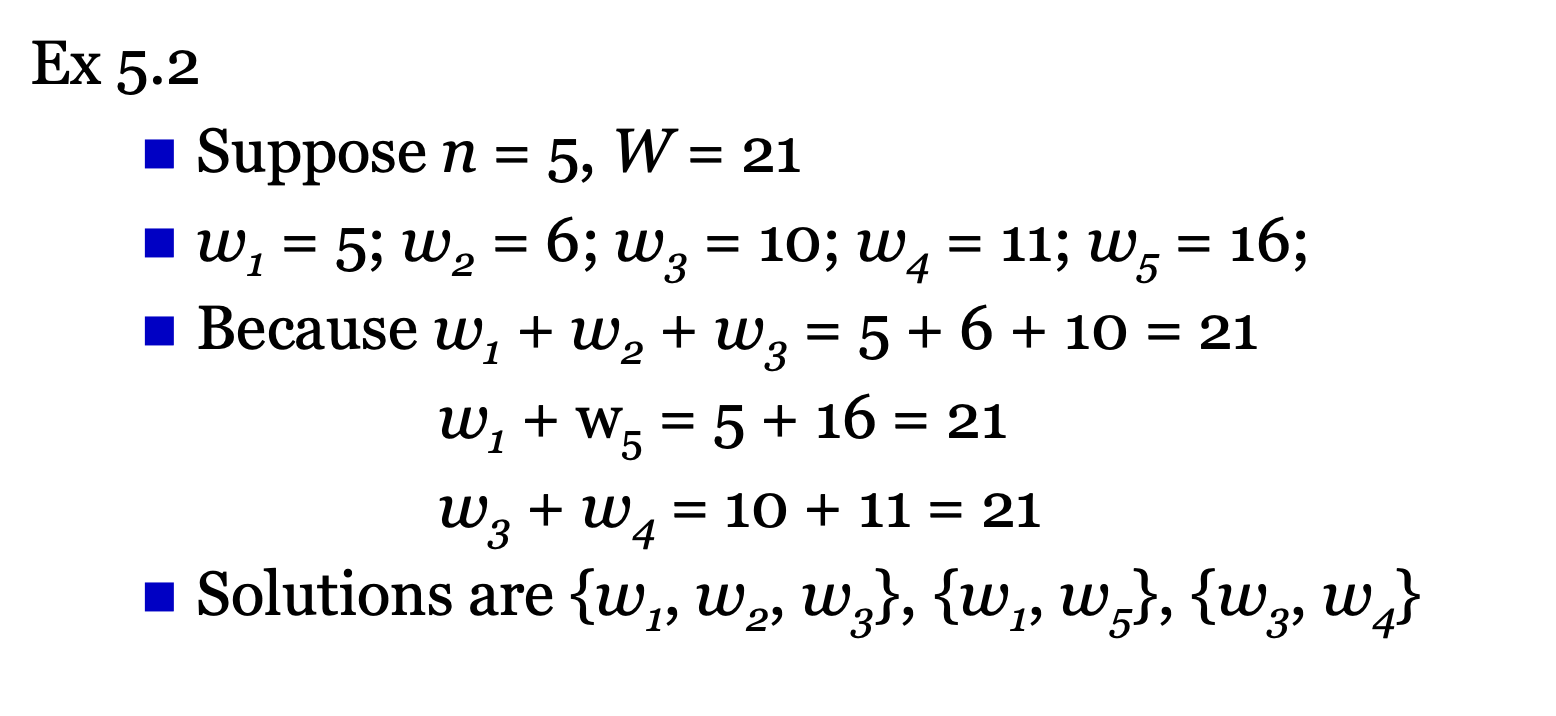
• 알고리즘 적용

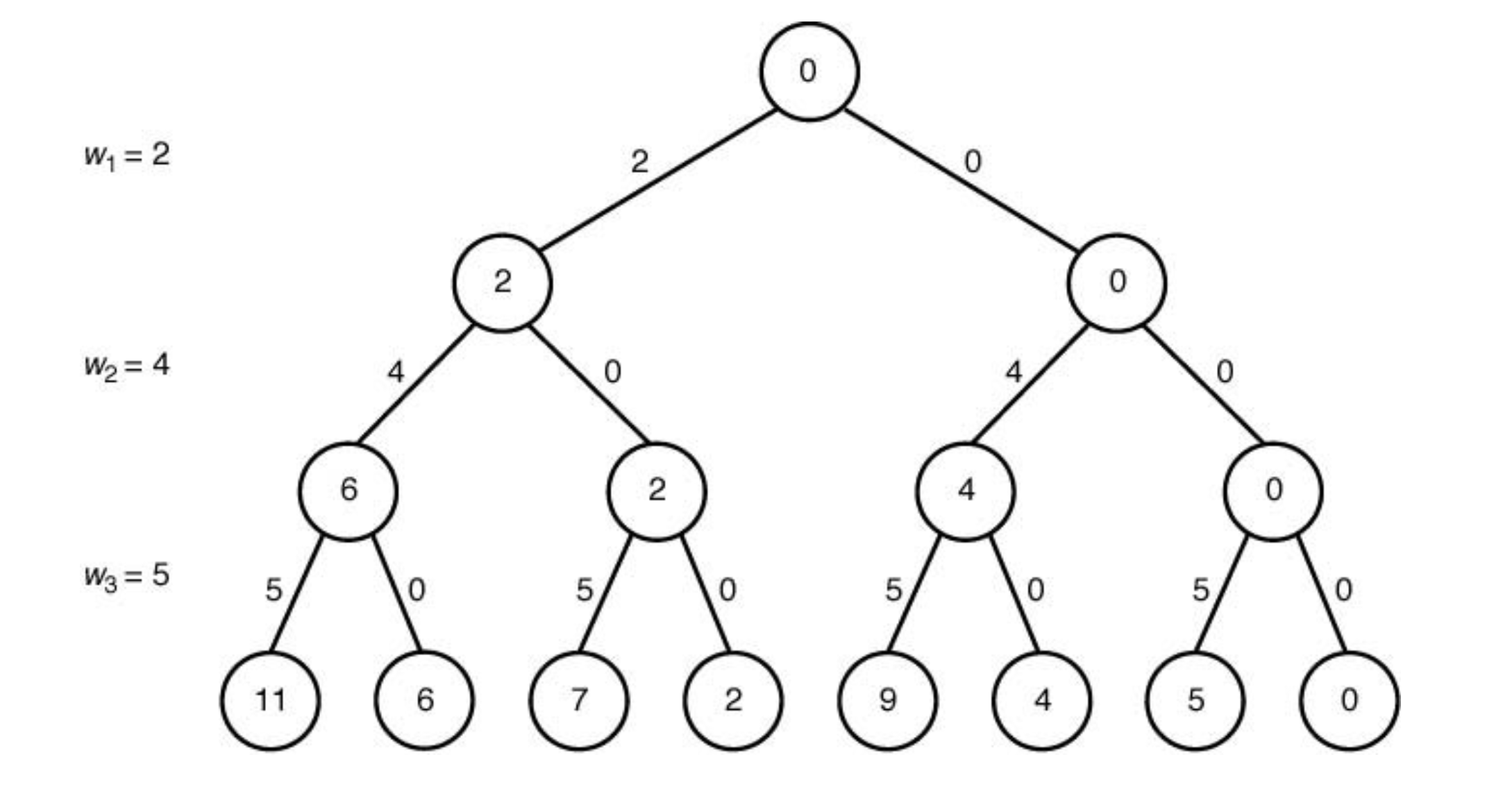
📁 시간 복잡도

시간복잡도 : $2^n$