[알고리즘] Minimum Spanning Tree

최원석·2024년 12월 17일

❓그래프 용어

용어 정리

비방향성 그래프 ( undirected graph )G = (V,E) → V 는 Set of Vertex → E 는 Set of Edge

경로 path

연결된 그래프 ( connected graph ) - 어떤 두 정점 사이에도 경로가 존재

부분 그래프 ( sub graph )

가중치 포함 그래프 ( weight graph )

순환경로 ( cycle )

순환적 그래프 (cyclic graph ), 비순환적 그래프 ( acyclic graph )

트리 tree - 비순환적이며, 연결된, 비방향성 그래프

뿌리 있는 트리 ( rooted tree ) - 한 정점이 뿌리로 지정된 트리

💫 Spanning Tree ( 신장 트리 )

연결된 비방향성 그래프 G에서 순환 경로를 제거하면서 연결된 부분 그래프가 되도록 이음선 제거
즉, 트리는 G안에 있는 모든 정점을 다 포함하면서 트리가 되는 “연결된 그래프 “

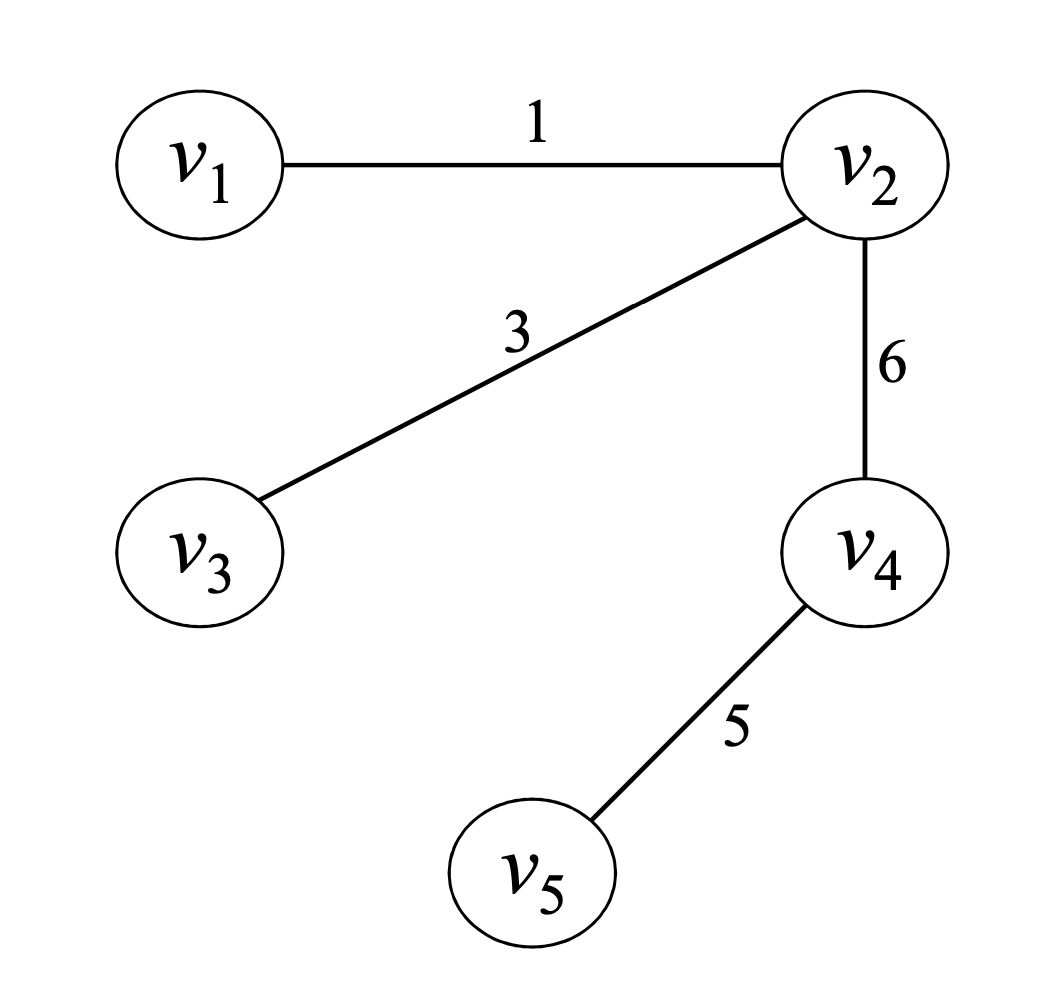
Spanning tree의 예시.

그래프를 보면 모든 정점들이 연결되어 있고 순환된 경로가 제거되어 있는 모습이다.

💫 Minimum Spanning Tree ( 최소비용 신장트리 )

A spanning tree with minimum weight

연결된, 비방향성 그래프 G에서 순환경로를 제거하면서 연결된 부분그래프가 되도록 이음선 제거

최소의 가중치를 가진 부분그래프는 반드시 트리가 되어야한다!

왤까..? 만약 트리가 아니라면 분명하게 순환경로(cycle)가 있을 것이다. 그렇게 되면 순환경로 상의 한 이음선을 제거하면 더 작은 비용의 신장트리가 되기 때문이다.

💫 Prim’s Algorithm

📁 수도 코드

F := 공집합; //  간선 집합 F를 빈 집합으로 초기화
Y := {v1}; // 정점 집합 Y에 첫 번째 정점 v1을 추가 <- v1 부터 시작
						// contain only the first one
While (the instance is not solved) {
select a vertex in V-Y that is nearest to Y; // 인스턴스가 해결되지 않았을 때(즉, 모든 정점이 MST에 추가되지 않았을 때) 반복합니다.
																					// feasibility check
add the vertex to Y;
add the edge to F;

if (Y == V) // solution check
the instance is solved;
}

📁 Prims Algorithm

void prim(int n, const number W[][], set_of_edges& F) {
 	index i, vnear; number min; edge e;
	index nearest[2..n]; number distance[2..n];
	F = 공집합;
	for(i=2; i <= n; i++) {  // 초기화
		nearest[i] = 1;		// vi에서 가장 가까운 정점을 v1으로 초기화
		distance[i] = W[1][i];	// vi과 v1을 잇는 이음선의 가중치로 초기화
	}

	repeat(n-1 times) {  // n-1개의 정점을 Y에 추가한다{
    min = “infinite”;
     for(i=2; i <= n; i++) // 각 정점에 대해서
    	 if (0 <= distance[i] <= min) { // distance[i]를 검사하여
     		min = distance[i]; // 가장 가까이 있는 vnear을
	 		vnear = i; // 찾는다.
		}
	  e = edge connecting vertices indexed by vnear and nearest[vnear]; 
      add e to F;
      distance[vnear] = -1;   // 찾은 노드를 Y에 추가한다.
      for(i=2; i <= n; i++)
      if (W[i][vnear] < distance[i]) {   // Y에 없는 각 노드에 대해서 
          distance[i] = W[i][vnear];    // distance[i]를 갱신한다.
          nearest[i] = vnear;
      }
	} 
}

nearest[i] = Y가 속한 정점 중에서 $v_i$ 중에서 가장 가까운 정점의 인덱스
→ distance 값이 작은지도 검사한다.

distance[i] = $v_i$ 와 nearest[i]를 잇는 이음선의 가중치

그래프의 표현

알고리즘 적용

📁 시간 복잡도

단위 연산 : repeat-루프 안에 있는 두 개의 for-루프 내부에 있는 명령문
입력 크기 : 마디의 개수, n
분석 : repeat - 루프가 n-1 반복

$T(n) = 2(n-1)(n-1)$

시간복잡도 : $n^2$

💫 Kruskal’s Algorithm

📁 수도 코드

F := 공집합; // initialize set of edges
				// to empty
create disjoint subsets of V, one for each
vertex and containing only that vertex;

sort the edges in E in nondecreasing order;

While (the instance is not solved) {
		select next edge; // selection procedure
		if (the edge connects 2 vertices
				in disjoint subsets) { // feasibility check
					merge the subsets;
					add the edge to F;
	}
	if (all the subsets are merged) // solution check
			the instance is solved;

}

📁 Kruskal’s Algorithm

void kruskal(int n, int m, set_of_edges E, set_of_edges& F) { 
 	index i, j;
    set_pointer p, q;
    edge e;
	Sort the m edges in E by weight in nondecreasing order; 
    F = 공집합;
	initial(n);
	while (number of edges in F is less than n-1) {
		e = edges with least weight not yet considered; 		
        i, j = indices of vertices connected by e;
		p = find(i);
		q = find(j);
		if (!equal(p,q)) {
			merge(p,q);
			add e to F; 
        }
	} 
}

Sort the m edges in E by weight in nondecreasing order;
크루스칼 알고리즘의 종료 조건은 MST에 포함된 간선의 수가 n-1이 될 때

코드를 보면 find(i) / find(j)를 볼 수 있다 이것이 뭘까..?
서로 집합 데이터를 이용해 검사를 한다.

코드를 보면 최소 가중치를 가지는 순서대로 간선들을 정렬하고 순서대로 추가하며 MS를 찾는다.
이때, cycle이 생길 수 있다. 그래서 집합안에 추가하고자 하는 vertax가 있는지 검사를 해야한다.

그래서 Disjoint Set Data Structur 를 사용한다.

📁 Disjoint Set Data Structure

Disjoint Set Data Structure 1

const int n = the number of elements in the universe;

typedef int index;
typedef index set_pointer; 
typedef index universe[1..n]; 

universe U;

// 원소 i에 대해 i 자신의 집합을 생성
void makeset (index i) { 
    U[i] = i; 
}

// 원소 i가 속한 집합의 대표 원소(루트)를 반환
set_pointer find (index i) { 
    index j; 
    j = i;
    while (U[j] != j) 
        j = U[j]; 
    return j; 
}

// p와 q가 속한 두 집합을 하나의 집합으로 합침
void merge (set_pointer p, set_pointer q) { 
    if (p < q) 
        U[q] = p; 
    else 
        U[p] = q; 
}

// p와 q가 같은 집합에 속하는지 확인
bool equal(set_pointer p, set_pointer q) { 
    if (p == q) 
        return TRUE; 
    else 
        return FALSE; 
}

// 모든 원소에 대해 각각의 개별 집합을 생성
void initial (int n) { 
    index i;
    for (i = 1; i <= n; i++) 
        makeset(i); 
}

Disjoint Set Data Structure 2

typedef index set_pointer; 

// 각 노드의 부모와 깊이 정보를 저장하는 구조체
struct nodetype { 
    index parent; // 부모 노드의 인덱스
    int depth; // 트리의 깊이 (랭크) 
};

typedef nodetype universe[1..n]; 

universe U;

// 원소 i에 대해 i 자신의 집합을 생성
void makeset (index i) { 
    U[i].parent = i; // 초기에는 자기 자신이 부모
    U[i].depth = 0; // 초기 깊이는 0
}

// 원소 i가 속한 집합의 대표 원소(루트)를 반환
set_pointer find (index i) { 
    index j; 
    j = i;
    while (U[j].parent != j) 
        j = U[j].parent; 
    return j; 
}

// p와 q가 속한 두 집합을 하나의 집합으로 합침 (랭크에 따른 합치기)
void merge (set_pointer p, set_pointer q) { 
    if (U[p].depth == U[q].depth) { 
        U[p].depth += 1; // 깊이가 같다면 p의 깊이를 1 증가
        U[q].parent = p; // q의 부모를 p로 설정
    } 
    else if (U[p].depth < U[q].depth) 
        U[p].parent = q; // p의 깊이가 더 작다면 p를 q의 자식으로 연결
    else 
        U[q].parent = p; // q의 깊이가 더 작다면 q를 p의 자식으로 연결
}

// equal과 initial 함수는 이전 버전과 동일
// equal: 두 원소가 같은 집합에 속하는지 확인
// initial: 모든 원소에 대해 각각의 개별 집합을 생성

// 최악의 비교 횟수: O(m log m)