💫 Dijkstra’s Algorithm
가중치가 있는 방향성 그래프에서 한 특정 정점에서 다른 모든 정점으로 가는 최단경로 구하는 문제
📁 수도 코드
F := 0;
Y := {v1};
While (the instance is not solved)
select a vertex v from V- Y, that has a shortest path // selection procedure
from v1, using only vertices in Y as intermediate; // and feasibility check
add the new vertex v to Y;
add the edge (on the shortest) that touches v to F;
if (Y == V) // solution check
the instance is solved;📁 Dijkstra’s Algorithm
void dijkstra (int n, const number W[][], set_of_edges& F) {
index i, vnear;
edge e;
index touch[2..n]; // v1부터 i까지의 현재 최단 경로에서 i 이전의 정점을 저장
number length[2..n]; // v1에서 i까지의 최단 경로의 길이를 저장
F = 공집합; // 최단 경로 트리의 간선 집합 초기화
// 모든 정점에 대해 v1을 경로의 마지막 정점으로 초기화하고,
// v1에서 i까지의 경로 길이를 초기화 (v1에서 i로 가는 간선의 가중치로 초기화)
for(i = 2; i <= n; i++) {
touch[i] = 1; // 초기에는 모든 정점의 이전 정점을 v1로 설정
length[i] = W[1][i]; // 초기에는 v1에서 정점 i로 가는 경로의 길이를 W[1][i]로 설정
}
// 모든 n-1개의 정점을 최단 경로 집합 Y에 추가
repeat(n-1 times) {
min = "infinite"; // 현재 최단 경로의 최소 거리를 무한대로 초기화
// 모든 정점을 검사하여 최단 경로를 가지는 정점을 선택
for(i = 2; i <= n; i++)
if (0 <= length[i] && length[i] <= min) {
min = length[i]; // 최단 경로의 최소 값을 갱신
vnear = i; // 최단 경로를 가지는 정점 vnear을 기록
}
// touch[vnear]에서 vnear로 가는 간선을 e로 추가
e = edge from vertex indexed by touch[vnear] to vertex indexed by vnear;
add e to F; // e를 최단 경로 트리에 추가
// vnear을 통해 연결된 정점들의 경로를 업데이트
for(i = 2; i <= n; i++)
if (length[vnear] + W[vnear][i] < length[i]) {
length[i] = length[vnear] + W[vnear][i]; // vnear을 통해 i로 가는 더 짧은 경로가 발견되면 업데이트
touch[i] = vnear; // 경로에서 i의 이전 정점을 vnear로 업데이트
}
length[vnear] = -1; // vnear를 Y 집합에 추가 (처리 완료)하고 더 이상 선택되지 않도록 함
}
}tounch[i] = 현재까지의 최단 경로에서, v1에서 vi로 가는 경로의 마지막에 위치한 Y에 속한 정점의 인덱스
length[i] = v1에서 vi로 가는 현재 최단 경로의 길이 Y에 속한 정점들만을 경유할 수 있음
(Y는 현재 최단 경로 집합을 의미)
- 알고리즘 적용

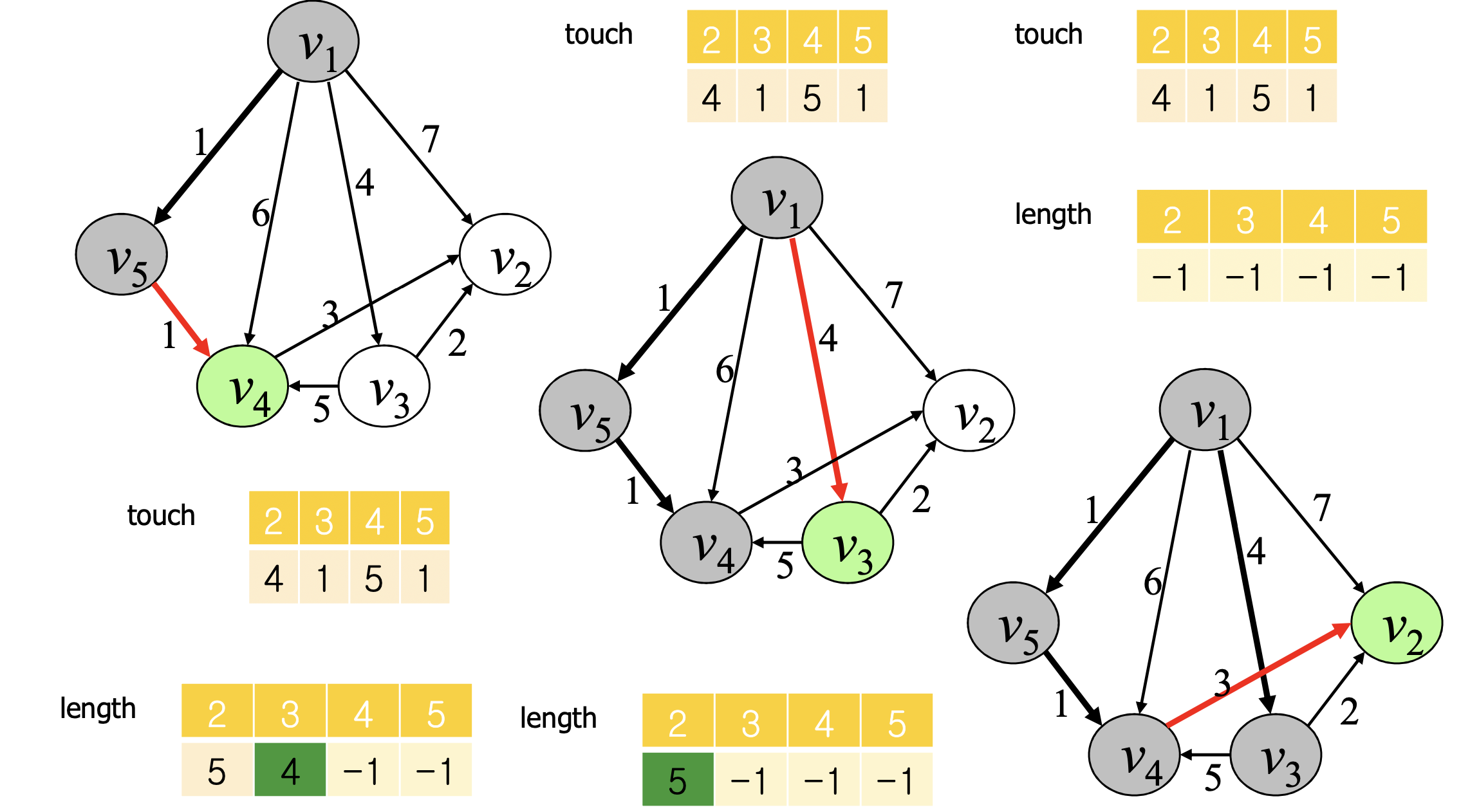
📁 시간 복잡도
시간 복잡도 :
