[알고리즘] The 0-1 Knapsack Problem

💫 The 0-1 Knapsack Problem

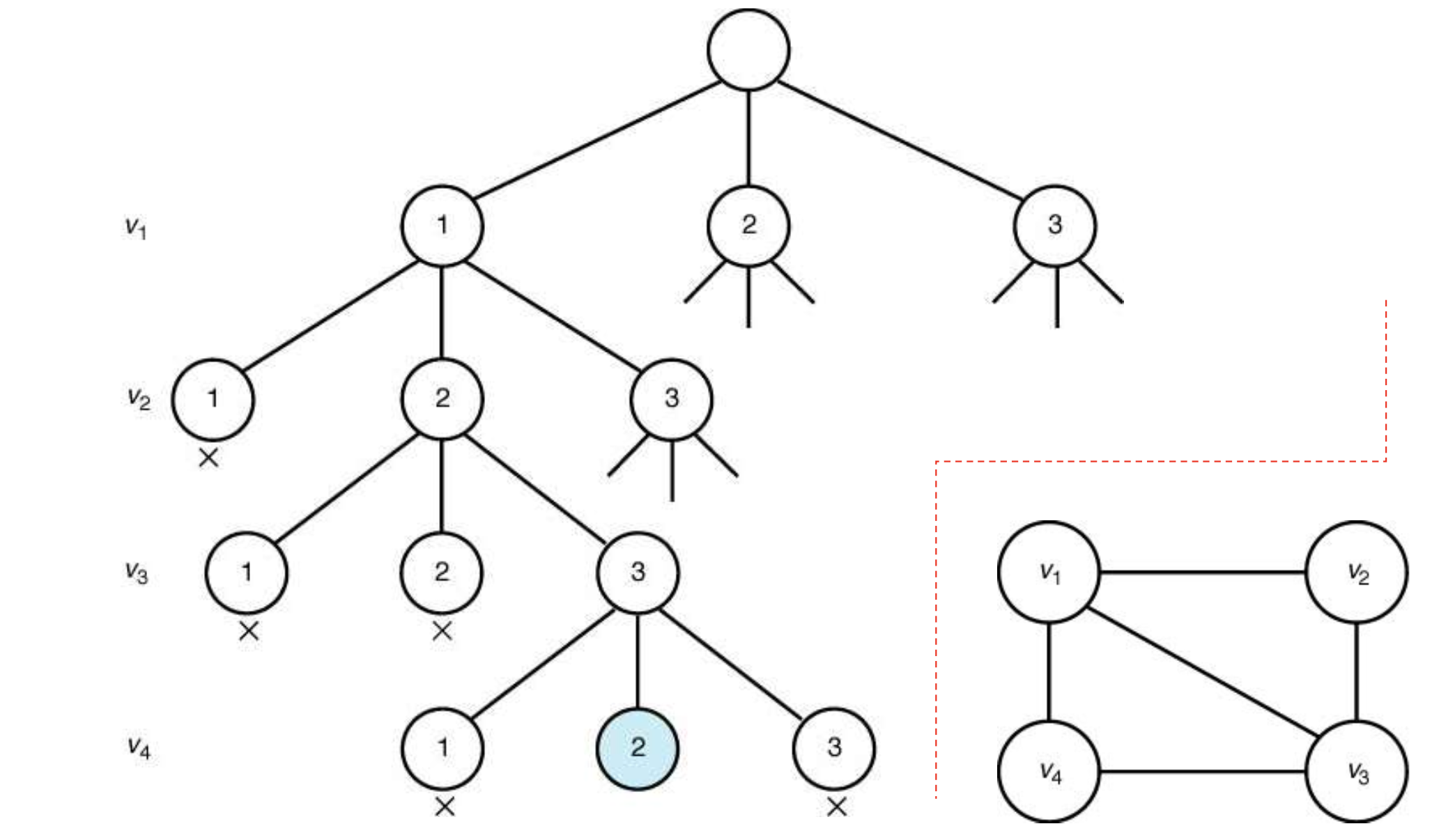
배낭 문제를 상태공간트리에 적용하여 문제를 해결한다.
뿌리마디에서 왼쪽으로 가면 첫번째 아이템을 배낭에 넣는 경우이고,오른쪽으로 가면 첫번째 아이템을 배낭에 넣지 않는 경우이다.

상태공간트리를 구출하여 되추적 기법으로 문제를 해결한다.

최적의 해를 찾는 문제이므로 검색이 완전히 끝나기 전에는 해답을 알 수 없다.

→ 검색하는 과정 동안 항상 이전까지 찾은 최적의 해를 기억해 두어야 한다.

📁 주요개념

알고리즘은 $w_i$ 와 $p_i$를 각각 i 번째 아이템의 무게와 값어치라고 하면, $p_i$/$w_i$ 의 값이 큰 것 부터 내림차순한다.

• profit : 그 노드에 오기까지 넣었던 아이템 값어치의 합
• weight : 그노드에 오기까지 넣었더 아이템 무게의 합
• bound : 노드가 수준 i에 있다고 하면, 수준 k에 있는 노드에서 총 무게가 W를 넘는다고 하자. 그리면 아래와 같이 bound응 구할 수 있다.

(weight< W ) and (bound> maxprofit )이면, 검색을 계속한다
→ 무게가 초과하지 않았고, 향후 가치가 최대 가치보다 클 수 있다면

이때, 계산을 하다보면 남은 아이템을 모두 넣어도 W를 넘지 않을 때에는 남은 아이템의 값어치를 bound에 다 더해주면 된다.

📁   The 0-1 Knapsack Problem

void knapsack (index i, int profit, int weight) {
    // 현재 무게(weight)가 배낭 용량(W)을 초과하지 않고,
    // 현재 이익(profit)이 최대 이익(maxprofit)보다 클 경우 최대 이익 갱신
    if (weight <= W && profit > maxprofit) { 
        maxprofit = profit; // 최대 이익 갱신
        numbest = i;        // 현재까지 가장 좋은 해에서 포함된 아이템의 인덱스 저장
        bestset = include;  // 현재 아이템 선택 상태를 최적 해(bestset)로 저장
    }
    
    // 현재 노드가 유망(promising)한 경우 탐색 진행
    if (promising(i)) {
        include[i+1] = "YES";  // 현재 아이템 w[i+1]을 포함시키는 경우
        knapsack(i+1, profit + p[i+1], weight + w[i+1]); // 다음 아이템 탐색 (포함)
        
        include[i+1] = "NO";   // 현재 아이템 w[i+1]을 포함하지 않는 경우
        knapsack(i+1, profit, weight); // 다음 아이템 탐색 (미포함)
    } 
}

bool promising(index i) {
    index j, k;
    int totweight;
    float bound;

    // 현재 무게(weight)가 배낭 용량(W)을 초과하면 유망하지 않음
    if (weight >= W)  
        return FALSE;

    else {
        j = i + 1;              // 다음 아이템 인덱스
        bound = profit;         // 현재까지의 이익으로 초기화
        totweight = weight;     // 현재까지의 무게로 초기화

        // 남은 배낭 용량으로 완전히 넣을 수 있는 아이템들을 추가
        while ((j <= n) && (totweight + w[j] <= W)) {
            totweight = totweight + w[j]; // 무게 누적
            bound = bound + p[j];         // 이익 누적
            j++;                          // 다음 아이템으로 이동
        }

        k = j; // 부분적으로 넣을 수 있는 첫 번째 아이템의 인덱스

        // 아직 고려하지 않은 아이템이 남아 있다면, 부분적으로 추가
        if (k <= n)
            bound = bound + (W - totweight) * p[k] / w[k];

        // 계산된 bound가 현재 최대 이익(maxprofit)보다 크면 유망
        return bound > maxprofit;
    }
}

• 알고리즘 적용

📁 시간 복잡도

시간복잡도 : $2^n$