💫 Brand and Bound
분기 한정법(Branch and Bound)은 최적화 문제를 해결하기 위한 탐색 알고리즘
-
backtrack 과 차이점
- 최적해를 찾을 가능성이 없으면 분기를 하지 않는다.
- 또한 Backtracking과 달리 최적화 문제를 푸는데만 사용한다.
-
설계전략
- 노드에서 숫자(경계)를 계산하여 다음을 결정, 노드가 유망한지 여부
- Bound는 이후 최적의 값을 예측하는 것.
- 최적의 값이 best로 기록된 solution보다 안 좋을 시 분기를 하지 않음.
💫 Breadth-First Search - 너비 우선 탐색
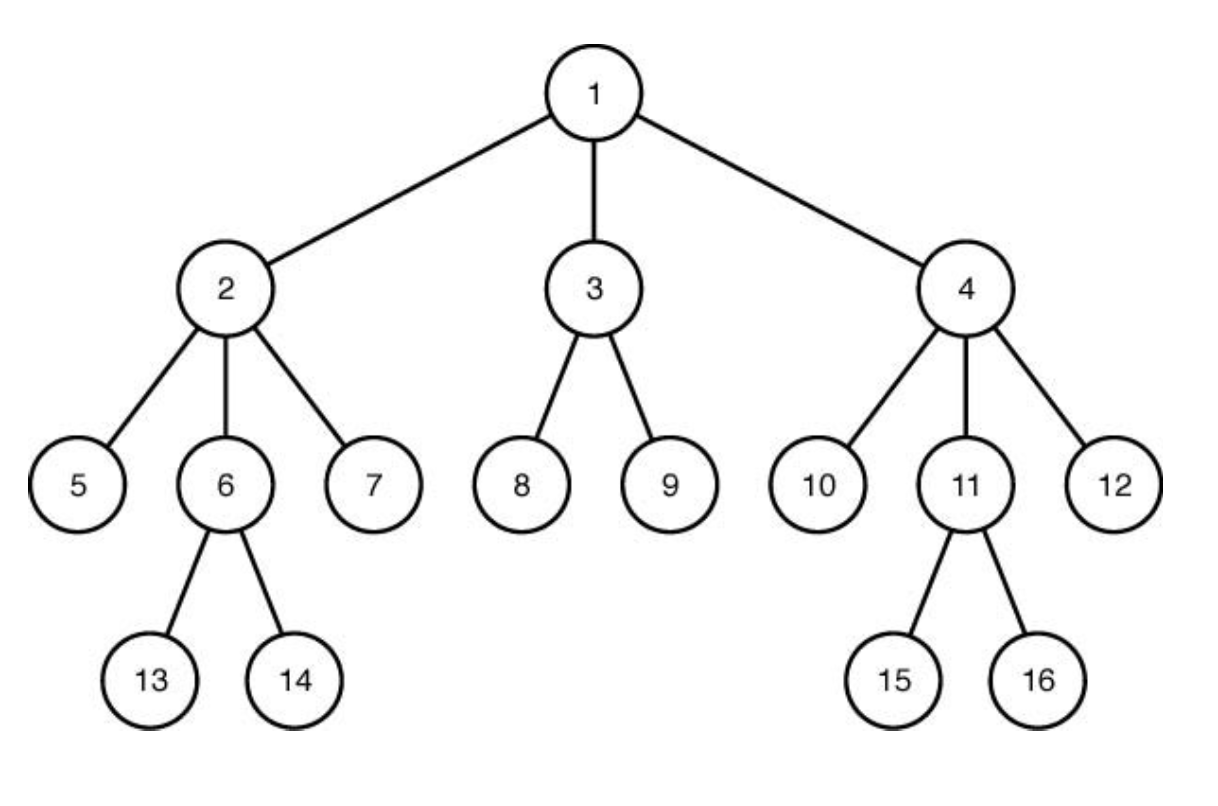
지금까지 봤던 알고리즘들과 다르게 같은 수준 (level)에 있는 노드들 먼저 검색한다. 왼쪽 → 오른쪽 순서로 검색한다.
📢 알고리즘은 Queue를 사용해서 구현한다.
void breadth_first_search(tree T) {
queue_of_node Q;
node u, v;
initialize(Q); // Initialize Q to be empty
v = root of T;
visit v;
enqueue(Q,v);
while(!empty(Q)) {
dequeue(Q,v);
for(each child u of v) {
visit u;
enqueue(Q,u);
}
}
}📁 0-1 Knapsack Problem - 분기 한정법
Queue 사용방법
void knapsack2(int n, const int p[], const int w[], int W, int &maxprofit) {
queue_of_node Q; // 노드를 저장할 큐
node u, v; // 현재 노드(v)와 확장 노드(u)
initialize(Q); // 큐 초기화
v.level = 0; // 초기 노드 설정 (루트 노드)
v.profit = 0; // 초기 이익 0
v.weight = 0; // 초기 무게 0
maxprofit = 0; // 초기 최대 이익 0
enqueue(Q, v); // 초기 노드를 큐에 삽입
// 큐가 비어 있지 않은 동안 탐색 반복
while (!empty(Q)) {
dequeue(Q, v); // 큐에서 노드 v를 꺼냄
u.level = v.level + 1; // u는 v의 다음 레벨(다음 아이템을 고려)
// u 노드가 아이템을 포함한 경우
u.profit = v.profit + p[u.level]; // u의 이익 = v의 이익 + 현재 아이템의 이익
u.weight = v.weight + w[u.level]; // u의 무게 = v의 무게 + 현재 아이템의 무게
if ((u.weight <= W) && (u.profit > maxprofit)) // u가 배낭 용량을 초과하지 않고, 최대 이익을 갱신할 수 있다면
maxprofit = u.profit; // 최대 이익 갱신
if (bound(u) > maxprofit) // u 노드의 bound가 현재 최대 이익보다 크면 탐색할 가치가 있음
enqueue(Q, u); // u를 큐에 삽입
// u 노드가 아이템을 포함하지 않는 경우
u.weight = v.weight; // u의 무게는 v의 무게와 동일
u.profit = v.profit; // u의 이익은 v의 이익과 동일
if (bound(u) > maxprofit) // u 노드의 bound가 현재 최대 이익보다 크면 탐색할 가치가 있음
enqueue(Q, u); // u를 큐에 삽입
}
}float bound(node u) {
index j, k; // j: 다음 아이템 인덱스, k: 부분적으로 넣을 아이템의 인덱스
int totweight; // 현재까지 배낭에 넣은 총 무게
float result; // bound 값을 저장할 변수
// 현재 노드의 무게가 배낭 용량을 초과하면 유망하지 않음
if (u.weight >= W)
return 0;
else {
result = u.profit; // 현재 노드까지의 이익을 result에 저장
j = u.level + 1; // 다음 아이템의 레벨로 초기화
totweight = u.weight; // 현재까지 배낭에 넣은 무게를 totweight에 저장
// 배낭 용량을 초과하지 않는 범위에서 가능한 모든 아이템을 완전히 넣음
while ((j <= n) && (totweight + w[j] <= W)) {
totweight = totweight + w[j]; // 무게를 누적
result = result + p[j]; // 이익을 누적
j++; // 다음 아이템으로 이동
}
k = j; // 부분적으로 넣을 수 있는 첫 번째 아이템의 인덱스
// 부분적으로 넣을 수 있는 아이템이 남아 있으면 계산
if (k <= n)
result = result + (W - totweight) * p[k] / w[k];
return result; // 계산된 bound 반환
}
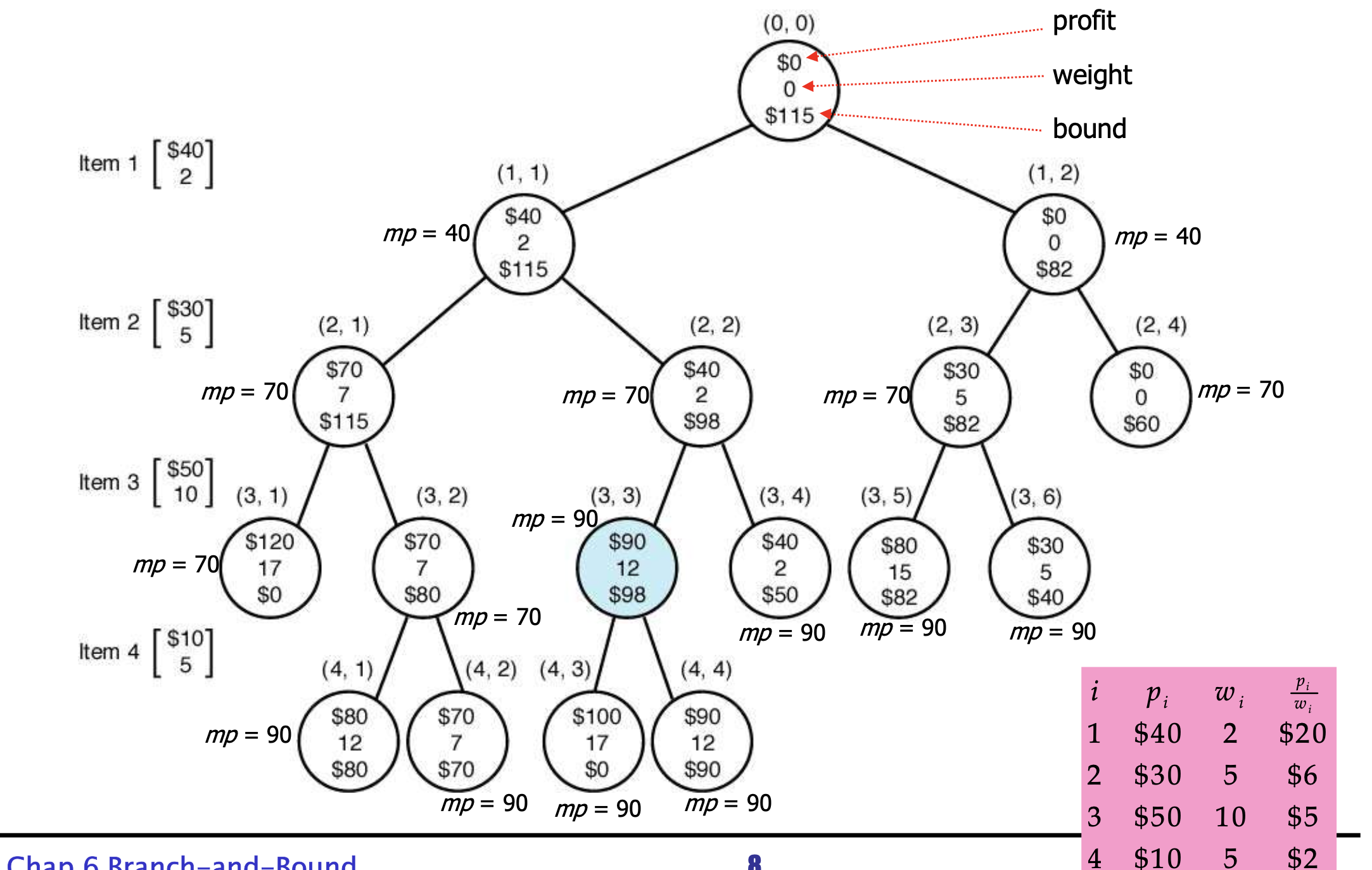
}분기한정 가지치기로 BFS를 하여 상태공간트리를 그려보면, 검색하는 노드의 개수는 17이다.
즉, backtrac보다 좋지 않다. 이것을 해결할 방법에 대해 알아보자!
📁 0-1 Knapsack Problem - 분기 한정법
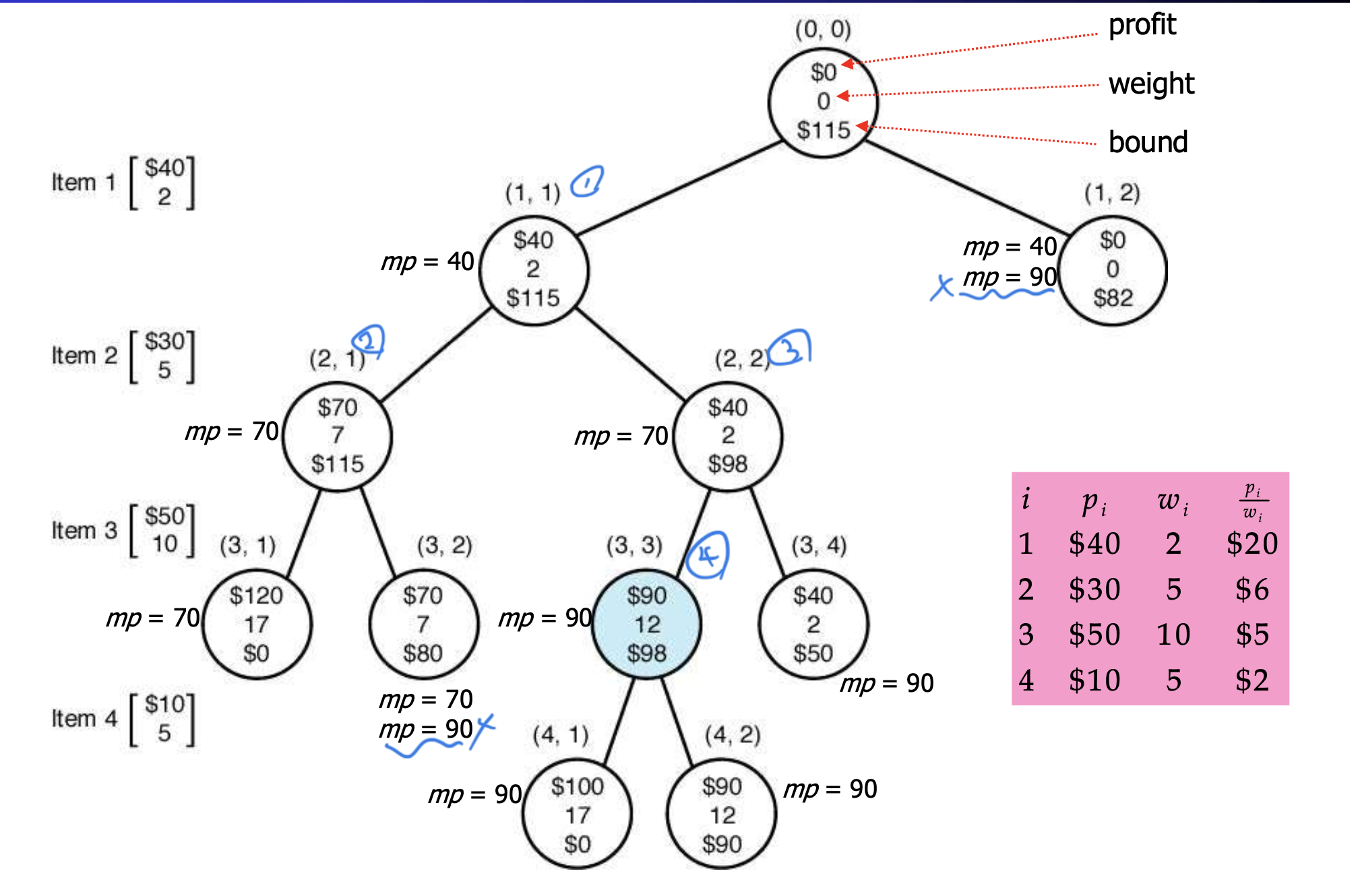
바로 우선순위 큐를 사용하는 방법이다.
void knapsack3(int n, const int p[], const int w[], int W, int &maxprofit) {
queue_of_node PQ; // 우선순위 큐(Priority Queue)
node u, v; // 현재 노드(v)와 확장된 자식 노드(u)
initialize(PQ); // 우선순위 큐 초기화
v.level = 0; // 초기 노드의 레벨 (루트 노드)
v.profit = 0; // 초기 노드의 이익
v.weight = 0; // 초기 노드의 무게
v.bound = bound(v); // 초기 노드의 bound 값 계산
maxprofit = 0; // 최대 이익 초기화
insert(PQ, v); // 초기 노드를 우선순위 큐에 삽입
// 우선순위 큐가 비어 있지 않은 동안 탐색 반복
while (!empty(PQ)) {
remove(PQ, v); // bound 값이 가장 큰 노드를 큐에서 꺼냄 (최적 후보 노드)
// 현재 노드가 여전히 유망한 경우 탐색 진행
if (v.bound > maxprofit) {
// u 노드를 v 노드의 첫 번째 자식으로 설정 (아이템 포함)
u.level = v.level + 1; // 다음 레벨로 이동
u.profit = v.profit + p[u.level]; // 현재 아이템의 이익 추가
u.weight = v.weight + w[u.level]; // 현재 아이템의 무게 추가
// u 노드의 무게가 배낭 용량을 초과하지 않고, 더 큰 이익을 제공할 경우 갱신
if ((u.weight <= W) && (u.profit > maxprofit))
maxprofit = u.profit; // 최대 이익 갱신
// u 노드의 bound 계산
u.bound = bound(u);
if (u.bound > maxprofit) // u 노드가 유망한 경우 큐에 삽입
insert(PQ, u);
// u 노드를 v 노드의 두 번째 자식으로 설정 (아이템 미포함)
u.weight = v.weight; // 현재 아이템의 무게는 그대로 유지
u.profit = v.profit; // 현재 아이템의 이익은 그대로 유지
u.bound = bound(u); // bound 값 재계산
if (u.bound > maxprofit) // u 노드가 유망한 경우 큐에 삽입
insert(PQ, u);
}
}
}💫 The Traveling Salesperson Problem
집이 위치하고 있는 도시에서 출발하여 다른 도시들을 각각 한번씩만 방문하고, 다시 집으로 돌아오는 문제
→ 가장 짧은 일주여행경로를 결정하는 문제
- 이 문제는 음이 아닌 가중치가 있는, 방향성 그래프로 나타낼 수 있다.
- 그래프 상에서 한 정점을 출발하여 다른 모든 정점을 한번씩만 거쳐서 다시 그 정점으로 돌아오는 경로
- 여러 경로 중 최소가 길이가 최소가 되는 경로
📁 동적계획법을 이용한 접근 방법 - 외판원문제
- V 는 모든 정점의 집합, A는 V의 부분 집합
📁 분기한정법 - 외판원문제
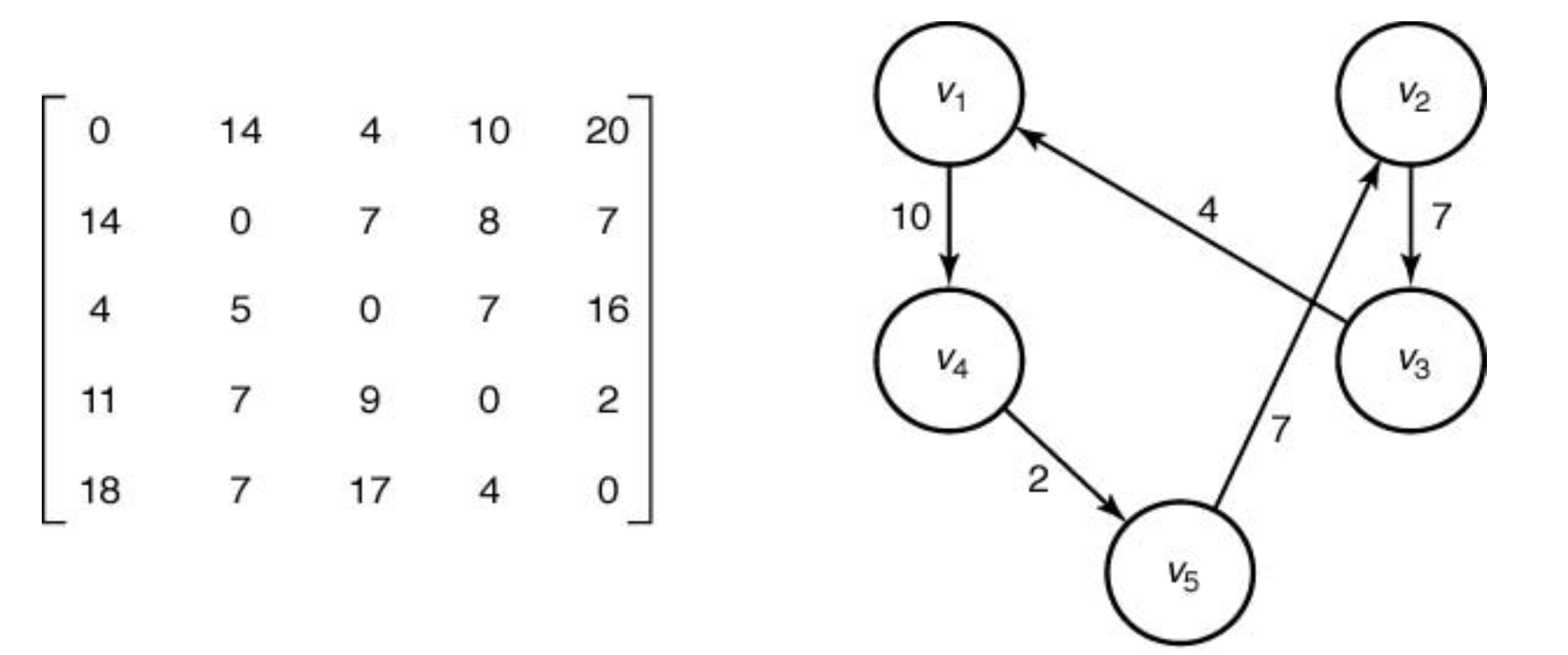
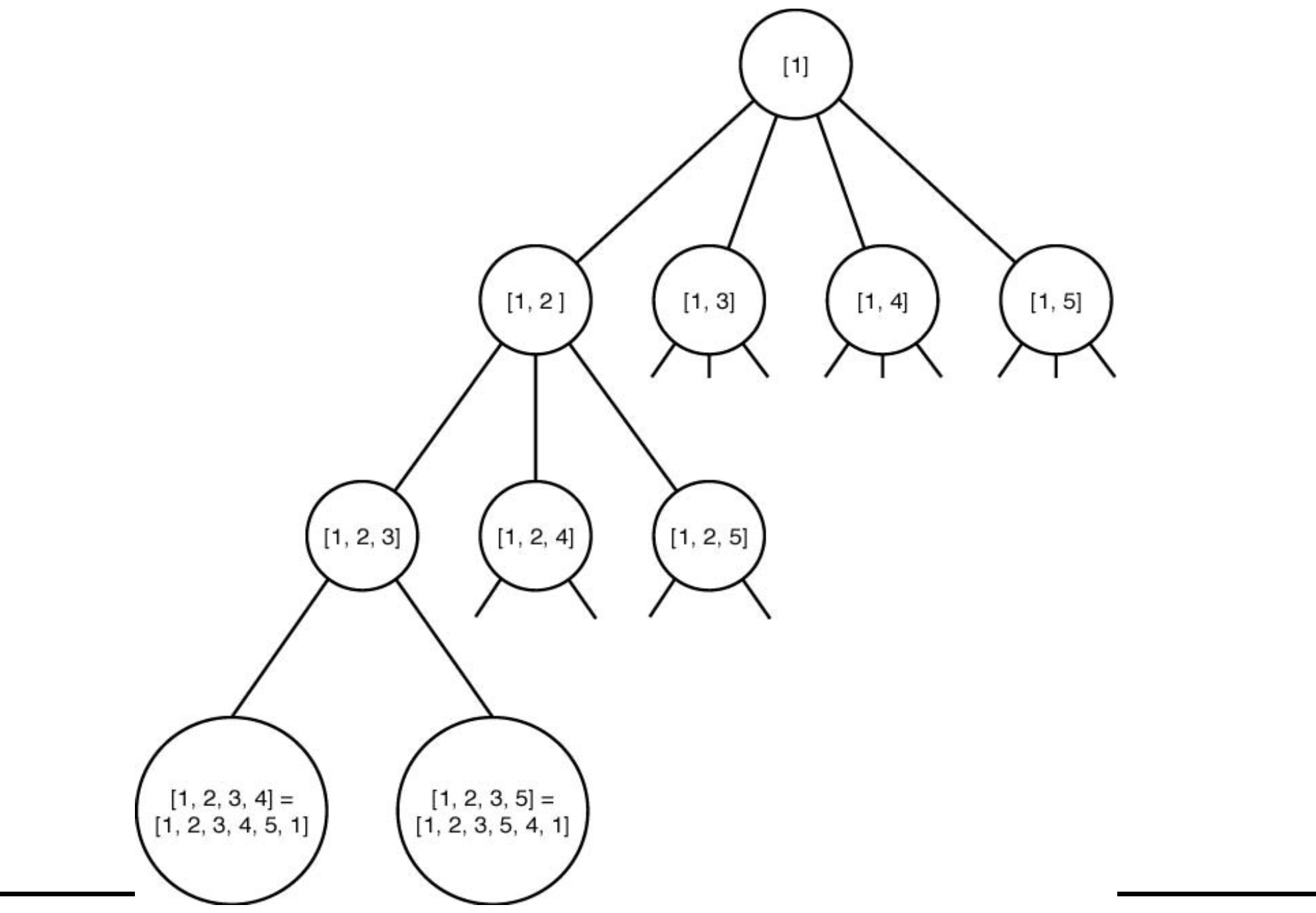
노드가 5개이기 때문에 4개의 마디까지만 그리면 된다.
📁 lower bounds
외판원문제에서 bound를 설정하는 것이다. 이때는 하한이다.


설명을 위해 예시의 값을 계산하면서 진행하도록 하겠다.
첫 번째로 초기 bound를 정할 때, 노드들의 합을 구한다.
v1 min(14, 4, 10, 20) = 4
v2 min(14, 7, 8, 7) = 7
v3 min(4, 5, 7, 16) = 4
v4 min(11, 7, 9, 2) = 2
v5 min(18, 7, 17, 4) = 4
4 + 7 + 4 + 2 + 4 = 21
1번 노드를 시작한다.
다음 으로 [1,2], [1,3], [1,4], [1,5] 노드들을 큐에 넣는다.
[1,3]에 대한 bound 계산
v2 min(14, 8, 7) = 7
v3 min(5, 7, 16) = 5 << - 1번에서 3번 노드로 이동하였기 때문에 1번노드로 이동하는 edge를 제거한다.
v4 min(11, 7, 2) = 2
v5 min(18, 7, 4) = 4
(현재 이동한 간선) + (나머지 간선들의 최소 값) = 4 + 7 + 5 + 2 + 4 = 22
…..
(생략)
계산 요약
- 이미 방문 한 노드의 간선의 가중치는 제외한다.
- 방문한 노드에서 방문하는 경우 출발지 ( 예시에서는 v1 )의 의 가중치도 빼야한다.
void travel2(int n, const number W[][], ordered_set &opttour, number &minlength) {
priority_queue_of_node PQ; // 탐색할 노드를 저장하는 우선순위 큐
node u, v; // 현재 노드(v)와 확장할 자식 노드(u)
initialize(PQ); // 우선순위 큐 초기화
v.level = 0; // 초기 노드는 레벨 0
v.path = [1]; // 시작 정점(1)에서 출발
v.bound = bound(v); // 현재 노드의 bound 계산
minlength = INFINITE; // 최소 경로 길이를 무한대로 초기화
insert(PQ, v); // 초기 노드를 우선순위 큐에 삽입
// 우선순위 큐가 비어 있지 않은 동안 탐색 반복
while (!empty(PQ)) {
remove(PQ, v); // 큐에서 bound가 가장 작은 노드를 꺼냄
if (v.bound < minlength) { // 현재 노드의 bound가 최소 길이보다 작을 때만 탐색
u.level = v.level + 1; // u는 v의 다음 레벨 노드
// 현재 경로(v.path)에 포함되지 않은 정점 i를 탐색
for ((all i such that 2 < i < n) && (i is not in v.path)) {
u.path = v.path; // u의 경로를 v의 경로로 초기화
put i at the end of u.path; // 경로 끝에 정점 i를 추가
// 모든 정점을 방문한 경우 (u.level == n-2)
if (u.level == n-2) {
put index of only vertex
not in u.path at the end of u.path; // 마지막 남은 정점을 추가
put 1 at the end of u.path; // 출발점(1)으로 돌아오는 경로 추가
// u의 경로 길이가 현재 최소 길이보다 작으면 갱신
if (length(u) < minlength) {
minlength = length(u); // 최소 경로 길이 갱신
opttour = u.path; // 최적 경로 갱신
}
}
else {
u.bound = bound(u); // u의 bound 계산
if (u.bound < minlength) // bound가 최소 경로 길이보다 작을 경우만 탐색
insert(PQ, u); // u를 우선순위 큐에 삽입
}
} // for 문 종료
} // if 문 종료
} // while 문 종료
}