네이버 AI 부트캠프 준비 - 6
이제는 강의를 다 들었기 때문에 강의에 나온 내용을 더 심화적으로 깊이있게
탄탄이 알아가는 단계라고 생각한다!
그래서 다음주까지는 기초를 더 심화있게 공부할 예정이다

깊이있게 공부할 내용들
- 선형대수학
- 인공지능 기초
- 백준 실버3이상 문제들
머신러닝에서 사용하는 방식의 시초인 퍼셉트론과 다층퍼셉트론인 신경망에 대해 적어보려고 한다!
퍼셉트론 기초 개념
다수의 신호(output)를 받아서 하나의 신호(input)로 출력한다
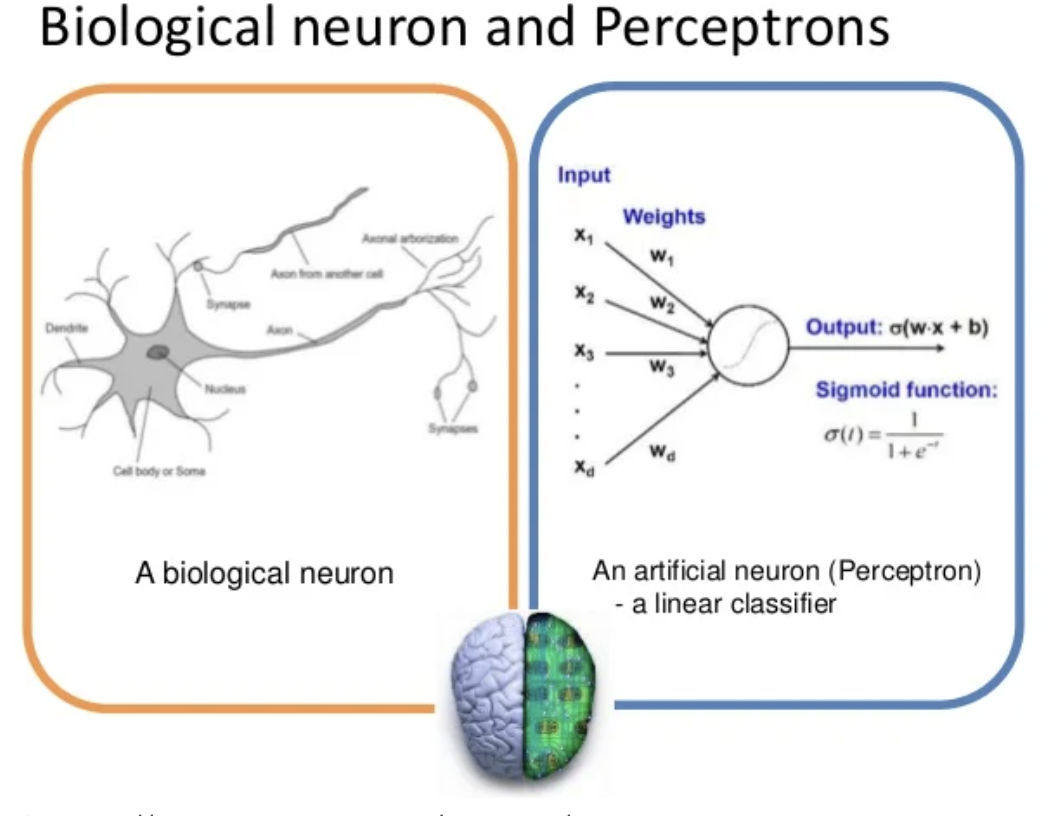
뉴런이 전기신호를 내보내 정보를 전달하는 것과 비슷!
가중치(weight)는 각각의 입력신호에 부여되어 계산을 하고 신호의 총합이 정해진 임계값(세타)을 넘었을때 1을 출력한다!
이를 뉴런의 활성화activation으로도 표현 - 못넘으면 0이나 -1출력
각 입력신호에는 고유한 weight가 부여되며 weight가 클수록 해당 신호가 중요하다!
여기서 기계학습이 하는 일은 이 weight의 값을 정하는 작업!
학습알고리즘에 따라 방식이 다를뿐 이 weight를 만들어내는 것이 학습이라는 차원에서는 모두 같다
퍼셉트론의 출력값이 1이나 0이기 때문에 선형분류!! 모형이라고 볼 수도 있다
보통 실수형의 입력벡터를 받아 이들의 선형조합을 계산하는 것 -> 백터의 내적과도 비슷
퍼셉트론 학습방법
처음에는 임의로 설정된 weight로 시작!
학습데이터를 퍼셉트론 모형에 입력하여 분류가 잘못되었을때 weight를 개선해 나간다
퍼셉트론은 모든 학습데이터를 정확히 분류 시킬때까지 선형적으로 학습!
한계가 명확하다
가중치와 편향
앞의 퍼셉트론 수식에서 나오는 세타@를 -b로 치환하여 좌변으로 넘기면
b+w1x1 + w2x2 < 0 => 1
b+w1x1 + w2x2 >=0 => 1
여기서 b를 편향이라고 할수있다(bias)
기계학습에서는 모델이 학습데이터 과적합(overfiting)되는것을 방지하는것이 중요!
과적합: 모델이 유연해서 학습데이터는 잘 분류하지만 다른 데이터는 분류 못하는것!
그래서 이 편향은 학습데이터가 가중치와 계산되어 넘어야하는 임계점으로
이 값이 높으면 높을수록 그만큼 분류의 기준이 엄격!
편향이 높을수록 모델이 간단해짐!-> 변수가 적고 더 일반화 되는 경우 - underfiting될수도 있다
요약하면, 가중치(weight)는 입력신호가 결과 출력에 주는 영향도를 조절하는 매개변수이고,
편향(bias)은 뉴런(또는 노드; x를 의미)이 얼마나 쉽게 활성화(1로 출력; activation)되느냐를 조정하는(adjust) 매개변수이다.
퍼셉트론 한계점
선형으로 나누기 힘든 XOR 같은 데이터 형태는 분류가 불가능하다!
그래서 다층 퍼셉트론을 사용!
신경망 Neural Network
퍼셉트론이 하나의 뉴런단위로 이루어진다면 각 뉴런이 모여 만든 하나의 뇌 -> 이게 신경망
일반적으로 단층 퍼셉트론 step function(임계값을 넘으면 1을 출력하는 함수)을 활성화 함수로 사용!
다층 퍼셉트론은 층이 여러개이며 sigmoid function을 활성화 함수로 사용하는 네트워크를 가리킨다
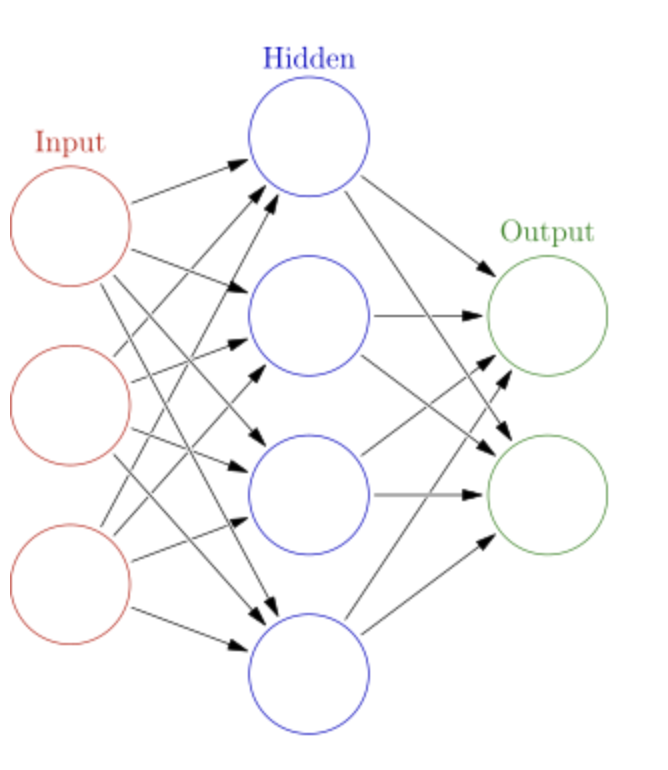
신경망은 input, hidden, output 이 있고, hidden 즉 은닉층은
입력층와 출력층과는 다르게 우리눈에 안보이기 때문에 은닉이라 부름
활성화 함수
input값이 weigth와 계산하여 다 더하고 사전에 설정한 임계값을 넘으면 1 아니면 0
활성화 함수도 무언가를 해주는 기능을 가진것으로 입력신호의 총합이 활성화를 일으킬지 아닐지를 결정
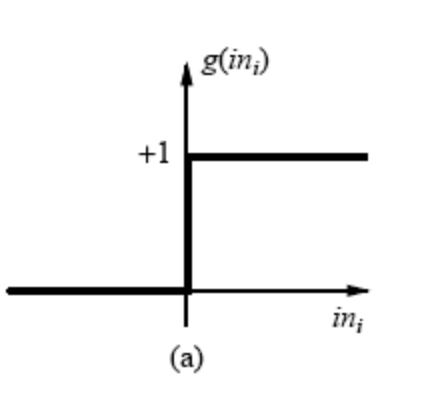
step function
단층 퍼셉트론이 이용!
특정 임계값을 넘으면 활성화!
지금 열심히 공부할때는 실력이 오르는지 모르지만 어느 순간 점수 확 오르는 것과 같은 상황!
sigmoid function
신경망에서 주로 사용!
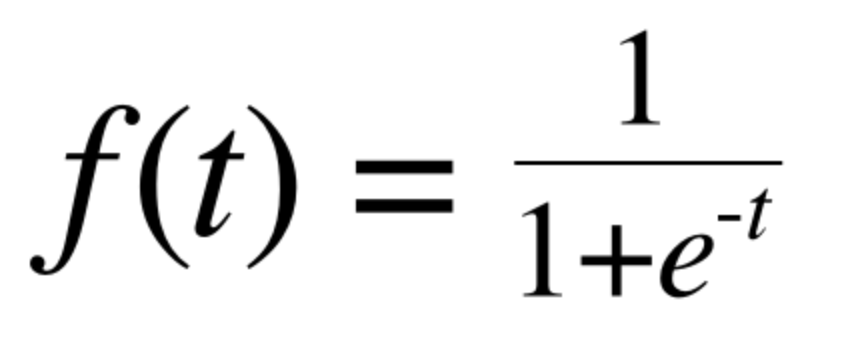
e는 자연상수로 2.7192라는 값을 가지는 실수이다
신경망에서는 입력신호를 받아서 변환하여 전달할 뿐임
완만한 곡선이어서 이것도 비선형!
특정경계를 기준으로 출력이 확바뀌어버리는 계단함수와는 달리
시그모이드 함수는 완만하게 매끄럽게 변화 -> 그래서 사용!
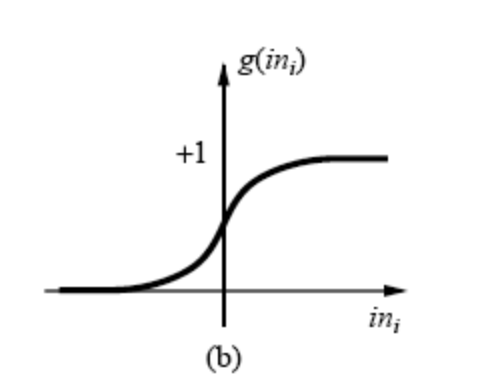
시그모이드 함수는 값을 실수형으로 가지는 것을 볼 수 있다.
시그모이드 함수의 매끄러움은 가중치 값을 전달할 때 좀 더 부드럽게 양을 조절해서 전달할 수 있다는 점이 계단 함수와 다른 점이다.
둘다 비선형인 점은 동일하다.
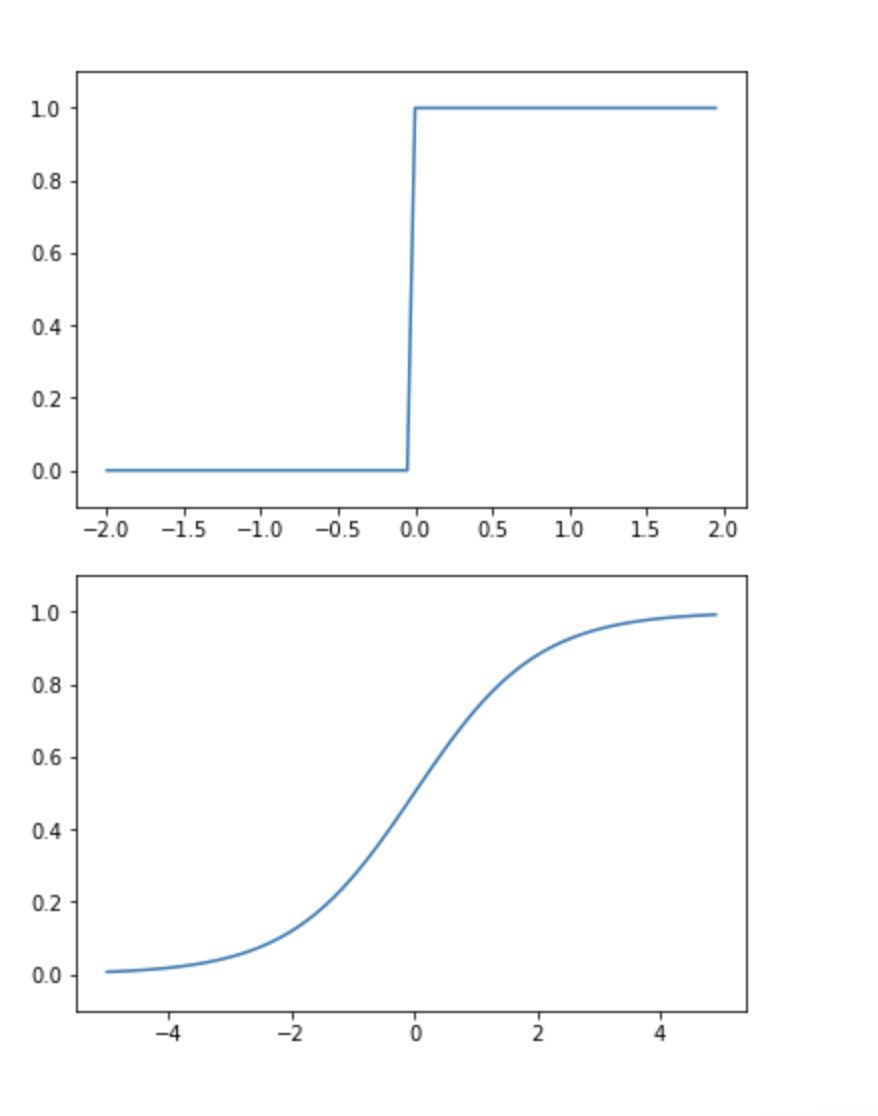
왜 비선형을 사용해야하나?
선형함수를 사용하면 은닉층을 사용하는 이점이 없다!
여러층 선형으로 구성해도 그냥 선형 3번 지난것 등 밖에 안됨!
출력층 설계
신경망은 분류(classfication)와 회귀(regression)문제에 모두 활용가능!
분류는 어떤 사람이 사기 쳤는지 , 안쳤는지 예측
회귀는 사기당한 금액이 얼마였는지
오차역전파, 경사 하강법
input에서 output으로 가중치를 업데이트 하면서 활성화 함수를 통해서 결과값을 가져오는것까지 배움
이렇게 오는것을 순전파(forward),-> 우리가 임의로 설정한 가중치 값이 input에 의해 업데이트 되었지만 많은 문제 있을수있음
역전파 방법은 결과값을 통해서 다시 역으로 input방향으로 오차를 다시 보내며 가중치를 재 업데이트 하는것!
물론 결과에 더 많은 영향을 미친 노드(뉴런)에 더 많은 오차를 돌려줌
-> input이 들어오는 방향(순전파)로 output layer에서 결과값나옴 ->이때 error 즉 오차를 가지는데
역전파는 error를 다시 역방향으로 hidden layer와 input layer로 오차를 다시 보내면서 가중치를 계산하면서 output에서 발생했던 오차를 적용
한번 돌리는것을 1 epoch 주기, epoch를 늘릴수록 가중치가 계속 업데이트(학습)되면서 점점 오차를 줄임
영향을 미친 만큼 오차를 다시 역전파한다!
경사하강법
경사하강법은 너무나 많은 신경망안의 가중치 조합을 모두 계산하면 시간이 오래걸리기 때문에 효율적으로 이를 하기 위해 고안된 방법
경사하강법을 사용하면 정확한답을 얻지는 못할수있음 -> 단계적으로 접근하기때문에 만족할만한 정확도 나올때까지 정답 찾아감
신경망의 오차를 경사하강법으로 최저 오차를 찾아나가는 방식이며 신경망의 계산 속도를 빠르게 한다
조금씩 -> 이게 너무 크면 최저점을 지나고 너무 적으면 최저를 못찾거나 엉뚱한 최저점을 찾을 수도 있다
("낮은 쪽의 방향을 찾기 위해 오차함수를 현재 위치에서 미분함")
- 함수의 최저점을 구하기 좋은 방법으로 신경망과 같이 계산해야 하는 양이 많고(선형대수학) 접근하기가 복잡한 수식에서 잘 작동
- 데이터가 불완전해도 유도리 있게 작동
피드백
경사하강법을 왜 사용해야하는지, 오차역전파는 왜 필요한지, 신경망이 어쩌다 나오게 되었는지
두번 정리하면서 더 자세히 깨닫게 되었다
AI부트캠프 후기를 매일 살펴보는데 BAT시험과 코테를 잘 준비해야 합격하니까 열심히 해보자!!