네이버 클라우드 자격증인 NCA를 합격하고 나서 자신감을 좀 얻은거 같다
심기일전해서 꼭 해보고 싶었던 네이버 AI부트캠프도 열심히 준비해보자!

Numpy 다시 정리
Numpy가 등장한 이유
어떻게 행렬과 매트릭스를 코드로 표현할까? => 이 물음에서 나왔다
Numpy의 장점
그냥 dot, norm을 리스트로만 처리한다면 처리속도 문제와 메모리 문제가 있을 수 있다
Numpy의 경우 고성능 과학용 패키지이며
일반 리스트에 비해 빠르고 메모리 효율적! ->
List와 다르게 dynamic not supported하다!
즉 다른 타입의 변수는 들어가지 못한다!
그리고 메모리에 순차적으로 들어가기 때문에
List(메모리 남는데에 아무데나 넣는, 그래서 주소값이 들어가있어서 한단계 더 거친다)보다 속도가 빠를수밖에 없다
c,c++통합도 가능
Numpy 사용법
import numpy as np 라고 해서 줄여서 많이 사용
t1 = np.array([1,4,5,6], float) => ndarray객체임, 하나의 데이터 타입만 가능!
만약 np.array(["1"], float) 이래도 1.0으로 나온다!
is는 메모리의 위치를 비교 하는데
list의 경우 a=[1,2] b=[2,1] a[0] is b[1] 하면 True가 나온다!
Numpy는 일단 순차적으로 들어가기 때문에 is로 검사시 False가 나온다!
Numpy 차원과 슬라이싱
t1.dtype # 데이터 타입이 나옴 float64, int8 등
np.array(a).shape # (3,3) 이라면 row가 3이고 col이 3인 행렬이다
ndim: Rank(열)의 개수를 의미! 1차원이면 1, 2차원이면 2가 나옴!!
nbytes: ndarray object의 메모리 크기를 반환 ->
np.array([1,2,3,4], float64).nbytes 이면 64비트는 8바이트여서
8*4 = 32 바이트이다!
np.array(t1).flatten() 이러면 다차원을 1차원으로 변경 가능
슬라이싱
a = np.array([ [1,2,3,4,5][6,7,8,9,10] ], int)
a[:,2:] 이렇게 작성하면 -> [[3,4,5][8,9,10]]
np.arange(1,31,0.5).reshape(2,30)
np.zeros(shape=(10,), dtype=int8)
identity
i행렬을 생성함, 단위행렬 즉 대각선인 1인 행렬이다!
np.identity(n =3, dtype=np.int8)
np.eye(3,5, k=2) # 이러면 row 3 col 5인 행렬이 만들어지고 2부터 아래 대각선으로 1씩 찍힌다
np.diag(t1, k=2) # 원래 있는 배열의 대각선 값 알고 싶을때 사용
sum
test1.sum(axis=1) # 이러면 col을 기준으로 계산한다!
모든 opreation 마찬가지로 적용 가능!
행 추가 하기
vstack이면 아래로 붙고 (col이 같아야함)
hstack이면 옆으로 붙는다 (row가 같아야함)
t1 * t2 를 할때 만약 행 열 개수가 같다면 각각의 원소끼리 곱해줌!
testa.dot(testb) 이게 내가 아는 앞의 열과 뒤에 행이 같아야만 하는 계산법!
test_a.T 를 하게 되면 전치 행렬! -> row col 바꾼다!
shape이 다르면 브로드 캐스팅을 하게 된다!
중요: for loop < list comprehension < numpy 임
AI블로그 정리
퍼셉트론
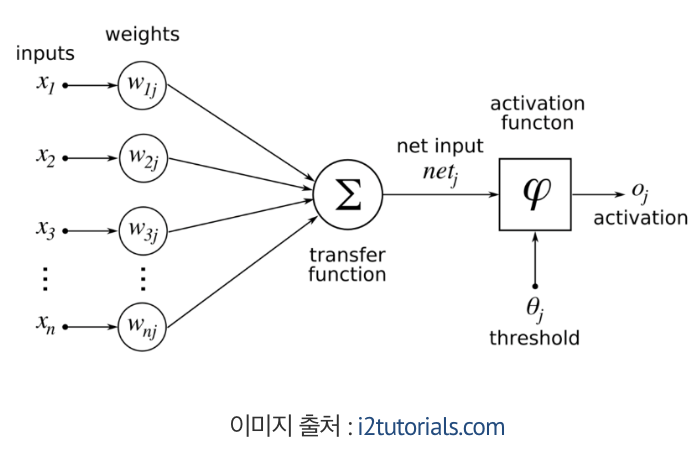
총 신호 5개를 입력 받는 (x1,x2.. x5) -> 각신호는 연산을 위한 가중 (w1,,,w5)를 가지고 있다
가중치는 각 신호가 주는 영향력을 조절하는 요소로 추후 학습 과정에서 이값을 업데이트!!
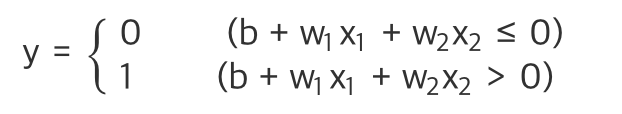
퍼셉트론은 모든 연산의 합이 임계값@을 넘으면 1, 못넘으면 0을 출력!
논리회로에서 XOR일때 단층 퍼셉트론으로는 하나는 1인데 하나는 0인 입력을 받지를 못해서
XOR을 해결할수없다!
그래서 MLP(Multi Layer Perceptron)으로는 표현 가능
신경만은 퍼셉트론을 쌓아올려 알아서 파라미터를 결정할 수 있는 장치
y = h(b+w1x1+ ... wnxn)
x>0 -> h(x) = 1
x <=0 -> h(x) = 0
h(x)는 활성화 함수라고 함 -> 가중치가 곱해진 신호의 총합이 활성화를 일으키는지 즉 임계값을 넘는지 판단
활성화 함수의 종류
일단 전부 비선형이다!
그 이유는 선형함수 f(x) = ax+b가 있다 가정!
l(l(l(x))) 처럼 층을 쌓는다 하더라고 결국 cx+d 형태를 벗어나지 못하기 때문에 의미가 없다!
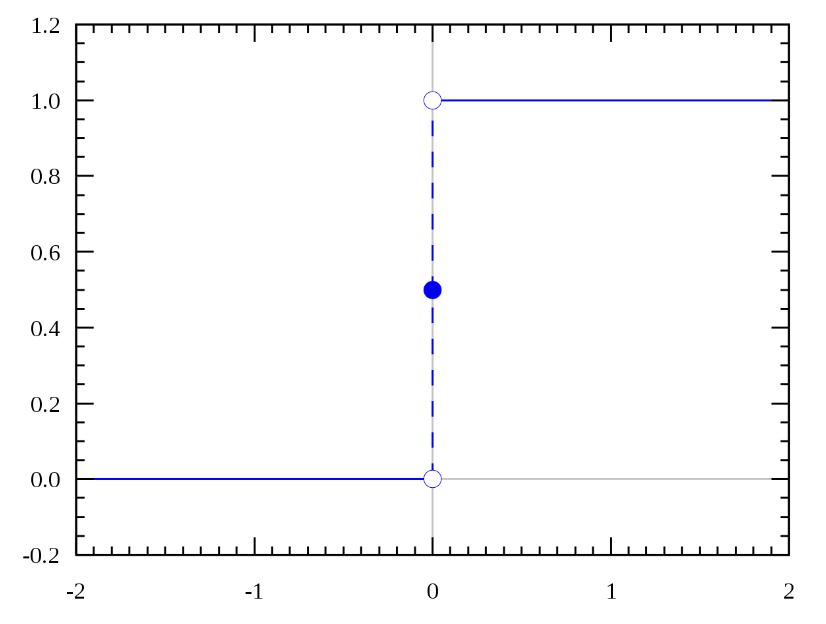
Step function
Sigmoid function & Hypertangent function
Step function
단층퍼셉트론에서 주로 사용 - 입력값의 합이 임계값을 넘으면 0 아니면 1
불연속이다 -> 그래서 미분이 불가능
다른지점에서 미분값이 0이 되버림 - 역전파 과정에서 미분값을 통해 학습을 하게 되는데 0이 되면 학습 못함
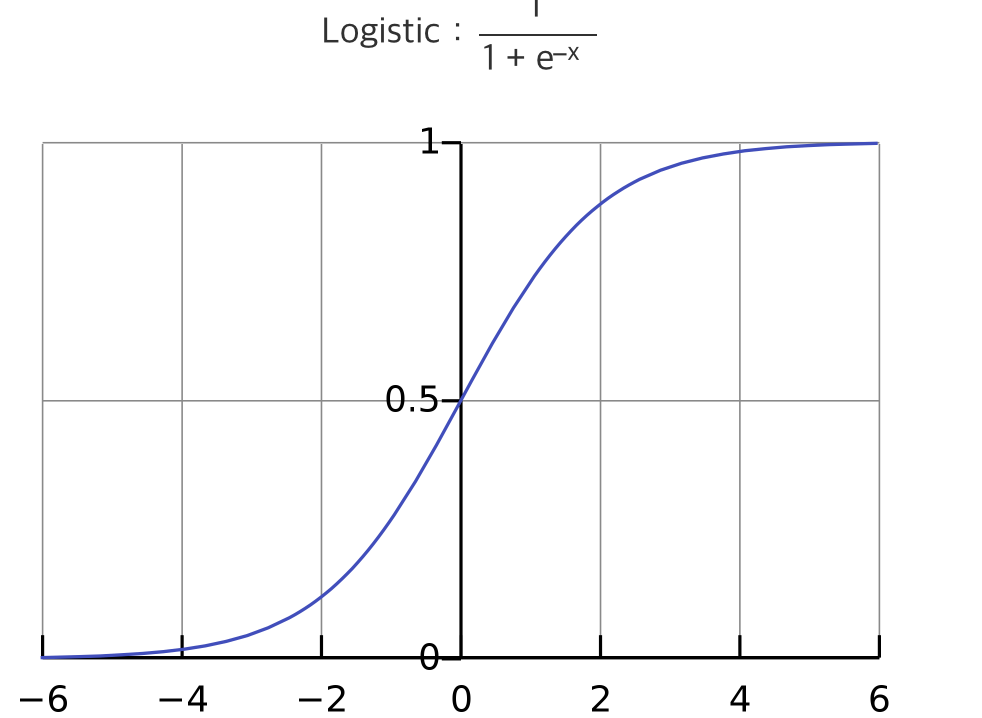
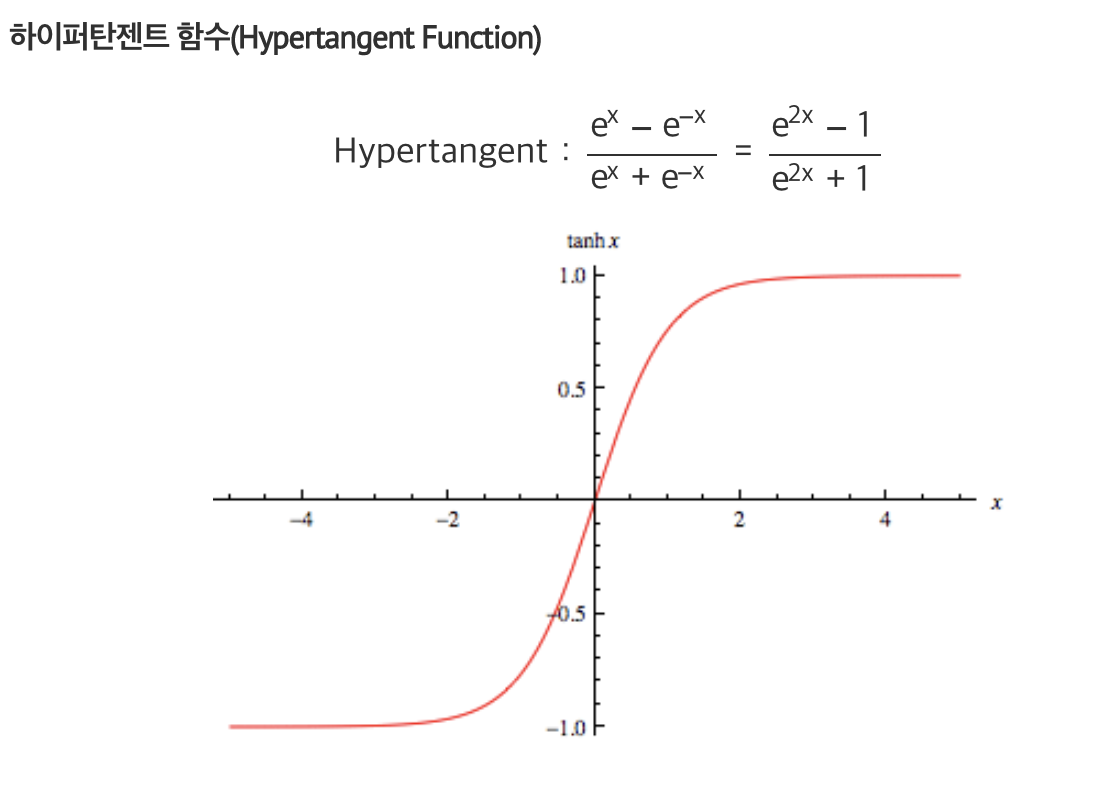
로지스틱 함수를 미분하게 되면
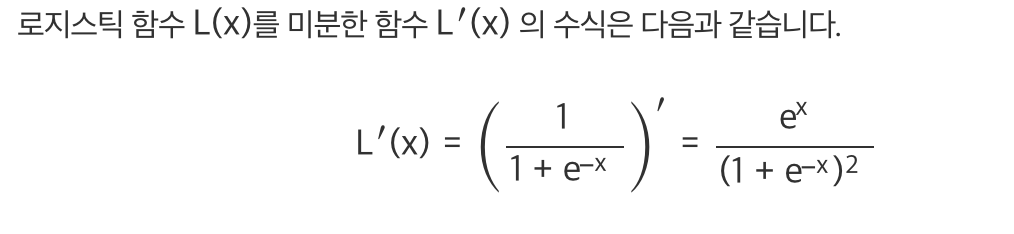
최댓값이 0.25밖에 되지 않고 0에 가깝다.. 그래서 층을 계속 쌓으면 결국 0이 되게 된다
하이퍼 탄젠트는 최댓값이1이어서 좀 덜하긴 하지만 여전히 미분값이 0 에근접하다
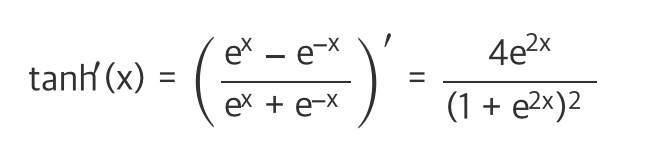
ReLU function & Leaky ReLU function
시그모이드 함수는 불연속이라는 계단의 한가지 단점을 해결
하지만 나머지 단점 하나 -> 미분했을때 즉 기울기가 0이 될수도 있다는 단점을 해결하지 못했다
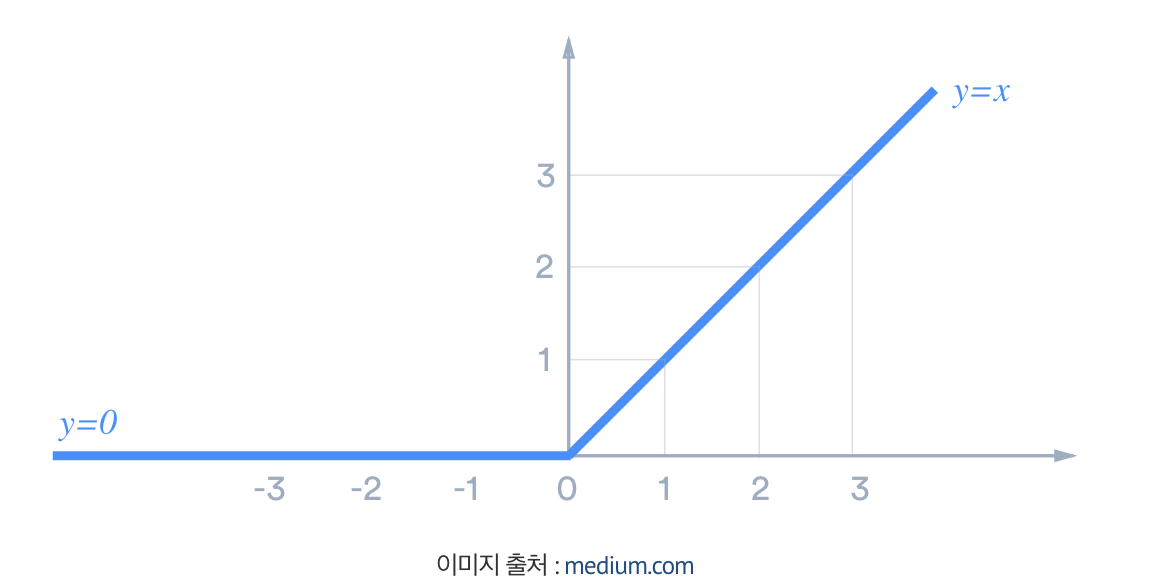
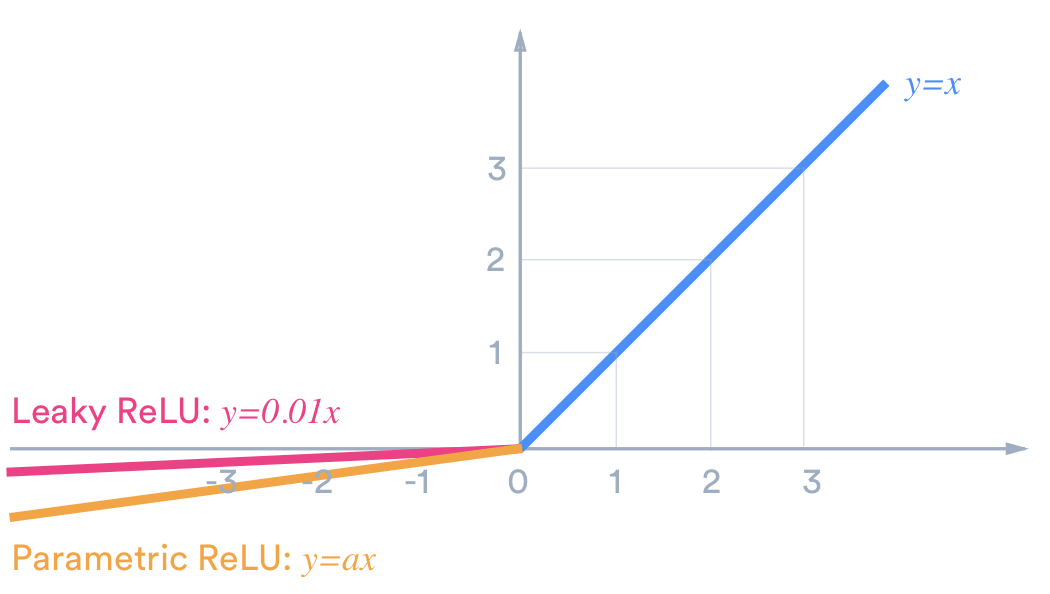
그래서 ReLU함수가 나왔다! 0보다 작으면 0을, 아니면 x그대로!
Softmax 함수
위에 적은 은닉층 활성화 함수들과 다르게 출력층의 활성화 함수로 사용
일반적으로 회귀(Regression) 즉 연속형 변수에 대한 예측값을 출력하는 경우
인스턴스를 다중 레이블로 분류 하는 것이 소프트 맥스 함수다!
이것은 지수함수여서 a값이 커지면 exp(a)값이 매우 커지기 때문에 오버플로우 되지 않게 조절해 줘야한다!
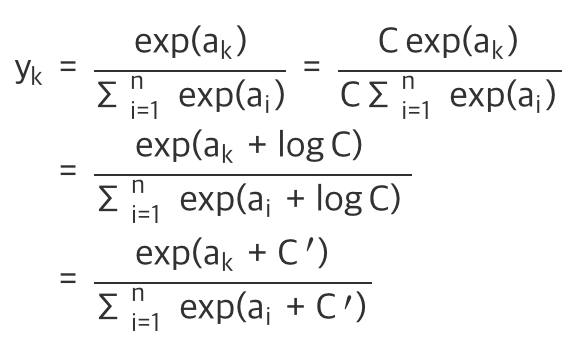
가중치 초기화
학습 시작 지점의 가중치를 잘 지정해주어야한다
Zero initialization & Random initialization
Zero initialization
모든 파라미터값을 0으로 둠!, 신경망의 파라미터가 모두 같으면 역전파로 갱신해도 모두 같은 값이나온다!
그래서 초기값은 무작위로 둬야한다!
Random initialization
확률분포를 사용하는 것, 정규분포를 이루는 값을 각 가중치에 배정하여 모두 다르게 설정
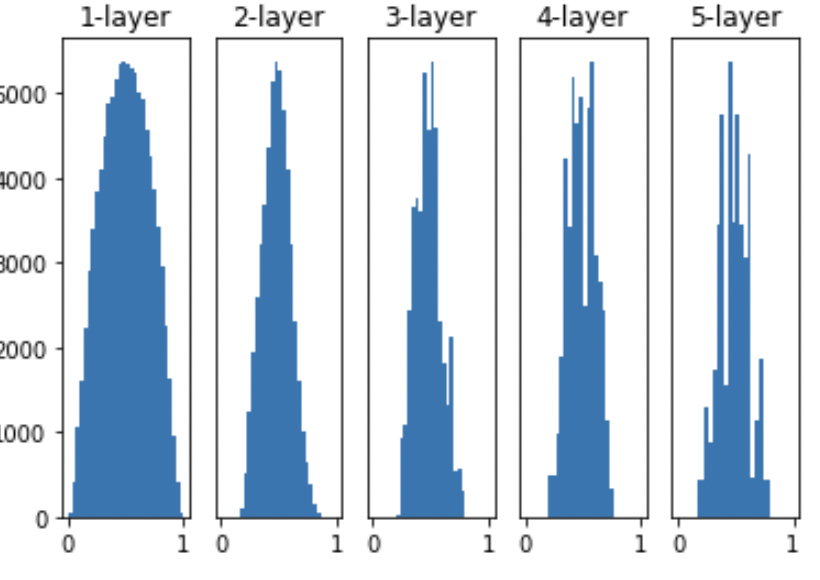
신경망은 100개의 노드를 5층으로 쌓음
표준편차가 1인 케이스 활성화 함수로는 시그모이드를 사용
활성화 함수로부터 0과 1에 가까운 값만 출력됨, 이러면 로지스틱함수의 미분값은 0에 가깝 -> 기울기 소실!!
Xavier initialzation & He초기화
사비에르 초기화는 Sigmoid에서 사용!
ReLU일때는 He초기화를 사용!
He초기화는 루트(2/n)를 표준편차로 하는 정규분포를 사용!
ReLU에 사비에르 적용하면 층 많아질때 기울기 소실됨!
손실함수와 경사 하강법
신경망은 파라미터를 더 좋은 방향으로 개선하도록 학습함 -> 이때 방향을 결정하는기준이 바로 손실함수
Loss function은 파라미터가 어떤 방향으로 개선되어야할지 판단하는 지표
MSE(mean square error)
회귀에서는 손실함수로 대게 평균제곱오차를 사용!
실제값과 예측값의 차이를 구한뒤 제곱한 값을 모든 인스턴스에 적용 /2 => 하나의 선으로 나온다
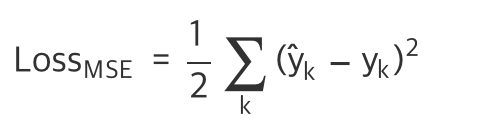
CEE(cross-entropy-error)
이진 분류에서는 교차 엔트로피를 주로 사용!
실제 레이블 [1 0 0 0 0]인 5개의 인소턴스에 대해 분류 1은 실제 예측값을 분류 2는 다른 예측값을 내놓음
교차레이블인 CEE는 실제 값과 일치시 오차가 0이 나온다
하지만 틀린다면 로그함수 log2가 있기 때문에 로그함수는 0으로 갈때 급격하게 -무한으로 발산하는 특성
레이블을 잘못 예측했을때 엄청 큰 손실값을 배정!
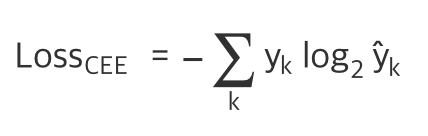
Gradient Descent
손실함수의 값이 크다는건 신경망의 모델의 성능이 좋지 않다는 것!
손실함수의 값을 줄이는 방향으로 진행해야 한다
경사 하강법을 하려면 경사(기울기)를 알아야 함! -> 미분을 사용
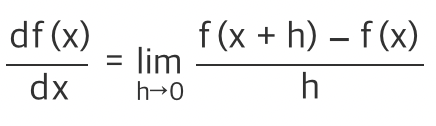
변수가 2개 이상일 경우에서는 편미분을 사용!(Partial derivative)
특정 변수 하나에 초점을 맞추어 미분을 하는 방식
g(x,y,z) = 3x^2y + xy^2z + 2x + yz
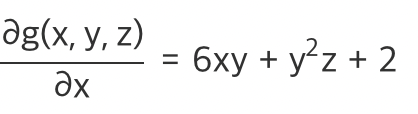
위에가 x에 대한 편미분!
손실함수의 변수가 여러개 일때 각 변수에 대한 편미분을 벡터로 묶어 정리한것을 Gradient라고 한다!
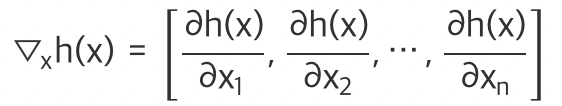
Descent(하강)
실제로 맞닥뜨리는 손실함수는 부분적으로 Convex함수임
즉 2차원 평면상 아래로 볼록한 그래프에서 에서 두 점을 잇는 직선을 g(x)라 할때
이때 구간 (x1,x2)사이의 점 xm에서 f(x) < g(x)입니다 -> 직선보다 아래로 볼록한 f(x)가 더 값이 낮으니까!
Convex함수에서는 어떤점에서 시작하더라도 내리막으로 움직이다면 최저점에 도달할수있다!
변수 xi에 대해서 편미분한 기울기만을 사용!
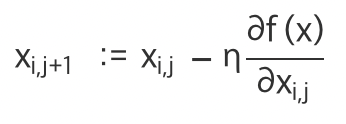
위 Xij+1은 새로 발을 내딛을 위치! -> 우변에 xij는 내가 있는 위치 @f(x)/@(xij)는 그 위치에서 기울기!
우리는 내려가야 하므로 원래 위치xij에서 기울기를 빼서 새로운 xij+1을 구하게 된다!
n은 여기서 learning rate 즉 학습률이다! 이 하이퍼파라미터는 기울기를 따라 얼마만큼 내려갈지를 결정
제대로된 학습률을 찾기 위해서는 적절한 학습률을 찾아야한다!
역전파와 순전파
순전파(forward Propagation)은 입력층 -> 출력층의 방향으로 계산하는 과정!
신호와 가중치를 곱한 값 출력층까지 차례대로 계산!
입력층의 노드가 2개, 은닉층의 노드가 3개, 출력층의 노드가 1개 x1,x2의 값은 1이며 레이블 y = 0
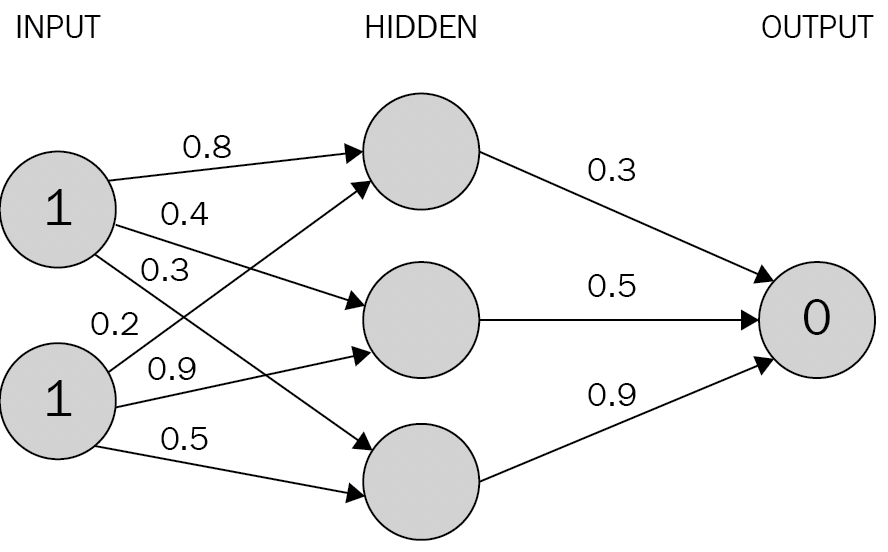
모든 층에 활성화 함수로 시그모이드(로지스틱)함수를 사용한다면
일단 은닉층에 들어갈 h1,h2,h3를 구한다
h1 = 1 0.8 + 1 0.2 = 1.0 , Sigmoid(h1) = 0.73
h2 = 10.4 + 1 0.9 = 1.3 , Sigmoid(h2) = 0.79
h3 = 10.3 + 10.5 = 0.8, Sigmoid(h3) = 0.69
출력되는 값 y는 0.73 0.3 + 0.790.5 + 0.69*0.9 = 1.235
Back Propagation(역전파)
실제 레이블 y=0이지만 순전파로 예측한 레이블 y^는 1.235임
1.235만큼의 오차가 발생!, 이제 손실함수를 통해 계산한 손실을 줄이는 방향으로 학습할 차례이다!
각 노드에 손실정보를 전달하는 과정을 역전파라고 함
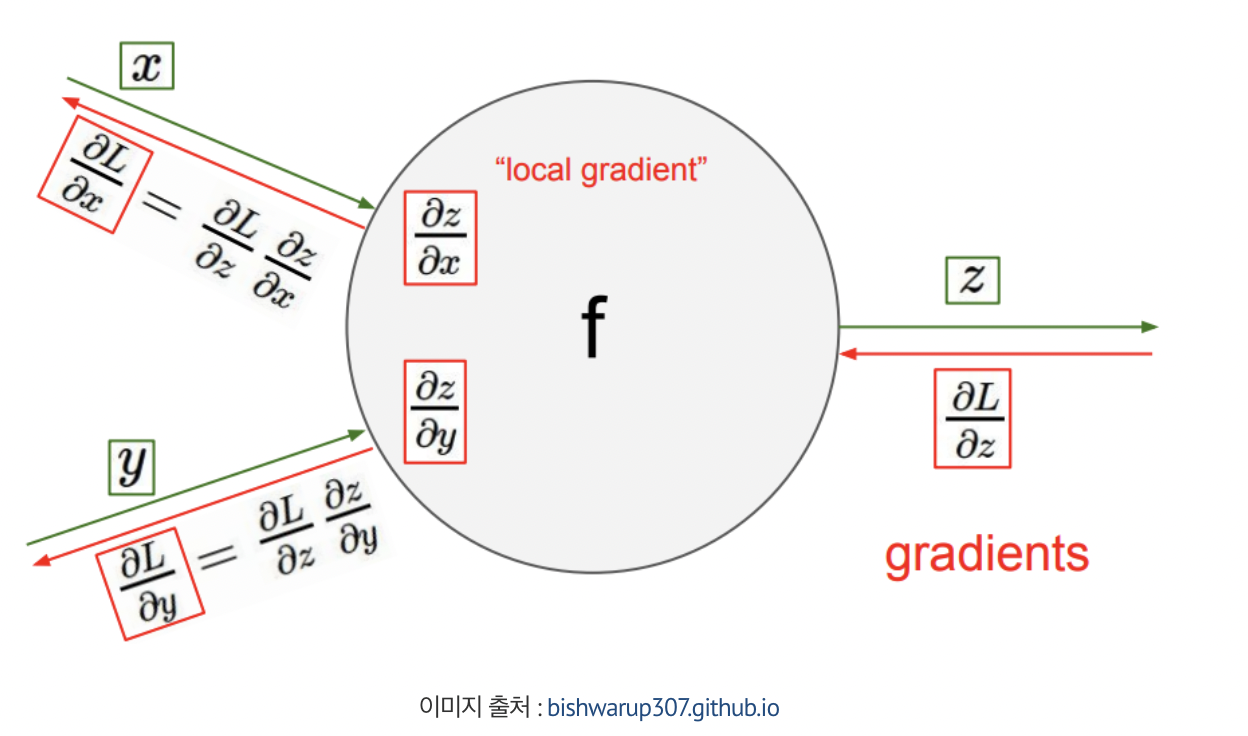
Optimizer
SGD, Momentum, MGD, Adagrad, NAG, Adadelta & RMSprop, Adam이 있다
SGD(Stochastic Gradient Descent)확률적 경사 하강법
한개의 데이터 셋만 사용하여 경사하강법을 사용! -> 파라미터 개선될때마다 다른 데이터를 선택
일반적인 경사하강법보다 속도는 빠르지만 오차가 있을수있음!
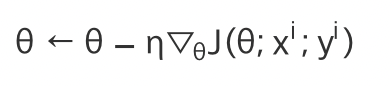
미니배치 경사하강법(MGD, mini-batch gradient descent)
하나보다 많은 n개의 미니배치를 학습단위로 사용!
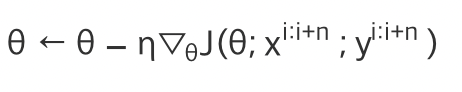
비등방성 함수 즉 방향에 따라 기울기 변화가 다른 함수에서 비효율적인 탐색 경로를 보인다!
모멘텀(Momentum)
운동량을 최적화 과정에 적용! 기울기가 큰 곳, 즉 그레디언트 변화가 심한 구간에서 값을 더 많이 변화시킨다!
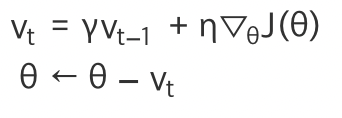
vt는 각 지점에서 속도! 확률적 경사하강법 식에 v를 곱한거!,이전 갱신에서 구한 속도가 다음 속도에 영향!
y =0 이면 확률적 경사하강법과 동일, y가 커지면 모멘텀 영향이 커진다!
NAG(nesterov Accelerated Gradient)
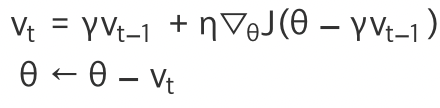
그레디언트의 변화를 그 자리에서 계산하지 않고 모멘텀에 의해서 이동한 곳에서 계산
모멘텀의 문제인 최소점 부군에서 그레디언트 변화가 갑자기 클때 최소점을 지날수도 있어서!!
NAG는 이전 위치에서 그레디언트를 계산하여 이런 사태에 대한위험도를 낮췄다!
학습방향을 어떻게 조정할 지 개선하는 과정에서 나온것들!
Adagrad
파라미터마다 다른 학습률을 적용하겠다
자주 등장하는 특정의 파라미터에는 낮은 학습률을, 가끔 등장하는 파라미터에는 높은 학습률을 지정!
훨씬더 강건(Robust)함
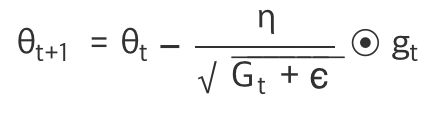
특정의 파라미터마다 다른 값을 적용하므로 i번째 특성의 그래디언트 gti를 아래와 같이 표기
각 파라미터 @i의 갱신은 다음과 같은 식을 통해서 진행
Gt는 t번째 학습에서 @i에 대한 그래디언트 제곱의 합을 나타냄, 옆의 이상한 기호는 안정성을 위한 작은 상수로
일반적으로 10^-8을 사용
저건 행렬의 원소별 곱셈을 의미 -> 즉 행열 같아서 각각 곱하는거!
Adagrad는 학습률을 적적히 적용함 하지만 학습률이 점점 줄어드는 문제는 있음
Adadelta & RMSprop( 지수 이동평균을 이용한 방법)
학습률이 0에 가까워지는 문제를 해결하기 위해 지수이동평균(Exponentia Moving Average, EMA)를 사용한 Adadelta가 나왔다.
Adam
Adam(Adaptive moment estimation, 아담)은
그래디언트 조정법(모멘텀, NAG 등)과 학습률 조정법(Adagrad, Adadelta, RMSprop)의 장점을 융합한 옵티마이저입니다
수학
fxgx 를 미분하면 => f(x)’g(x) + f(x)g(x)’
f(x) / g(x) 를 미분하면 => (f’g - g’f) / g^2
연쇄법칙 -> f(g(x))’ => f’(g(x)) g(x)’
y = (3x^2+2)^2를 미분한다 했을때
a = 3x^2 + 2이라면, y = a^2, a=3x^+2 두함수의 합성함수로 볼수있다!
2(3x^2+2)* (6x)