다양한 블로그들을 보고 네이버 Precourse에 나온 강의들의 퀴즈들을 풀어보며
나의 지금 위치와 현재 수준을 느끼는 중이다..ㅋㅋ
최근 네이버 AI부트캠프 합격자 블로그를 보니 코테가 굉장히 어렵게 나온다고 해서
프로그래머스 코딩테스트를 위주로 공부를 하고 있다
오늘부터 바뀐 공부 작업
오늘부터는 매일 8문제 -> 1시간반에 4문제씩 풀고 1시간 해설 보고 남은 문제 시간재서 풀기
그리고 저녁 먹고 당일 못 푼 문제들 다시 풀어보기!
AI부분은 퀴즈들 전부 알때까지 개념에 충실한 심화 내용들 찾아보기 + 내가 적은 블로그들 매일 보기
이제 대략 10일정도 남았는데 후회없이 해봐야겠다!

CNN 내용 정리
합성공 신경망은 두 종류의 층으로 이루어짐
Convolutional layer와 Pooling layer로 이루어졌다!
차고로 input이 얼마나 들어와도 파라미터와 함수는 동일하다!
Convoultional layer (합성곱 층)
합성곱 층은 입력데이터에 특정 크기의 커널을 적용하여 새로운 출력값을 계산하는 역할
-
패딩
입력 주변을 특정값으로 채우는 것을 의미! 위아래, 왼쪽오른쪽 다 채워짐! -
스트라이드
커널을 적용하는 위치의 간격, 즉 얼마나 띄엄띄엄 검사할지
입력데이터 높이와 너비를 H,W 커널의 높이와 너비는 KH KW 그리고 패딩 스트라이드 P S

그래서 입력이 5X5 이고 패딩이 1 스트라이드가 1 커널이 3이면
(5+ 2X1 -3)/1 X (5+2X1-3)/1 = 4 X4 가 나온다!
Color 이미지가 적용되면 이미지의 차원이 더 늘어남 -> RGB값을 적용하기 때문에!
Pooling layer
가로 세로 방향의 공간을 줄이기 위해 풀링을 수행
이때는 파라미터가 0이다!
최대 풀링과 평균 풀링이 있다!-> 일반적으로 최대 풀링을 사용!
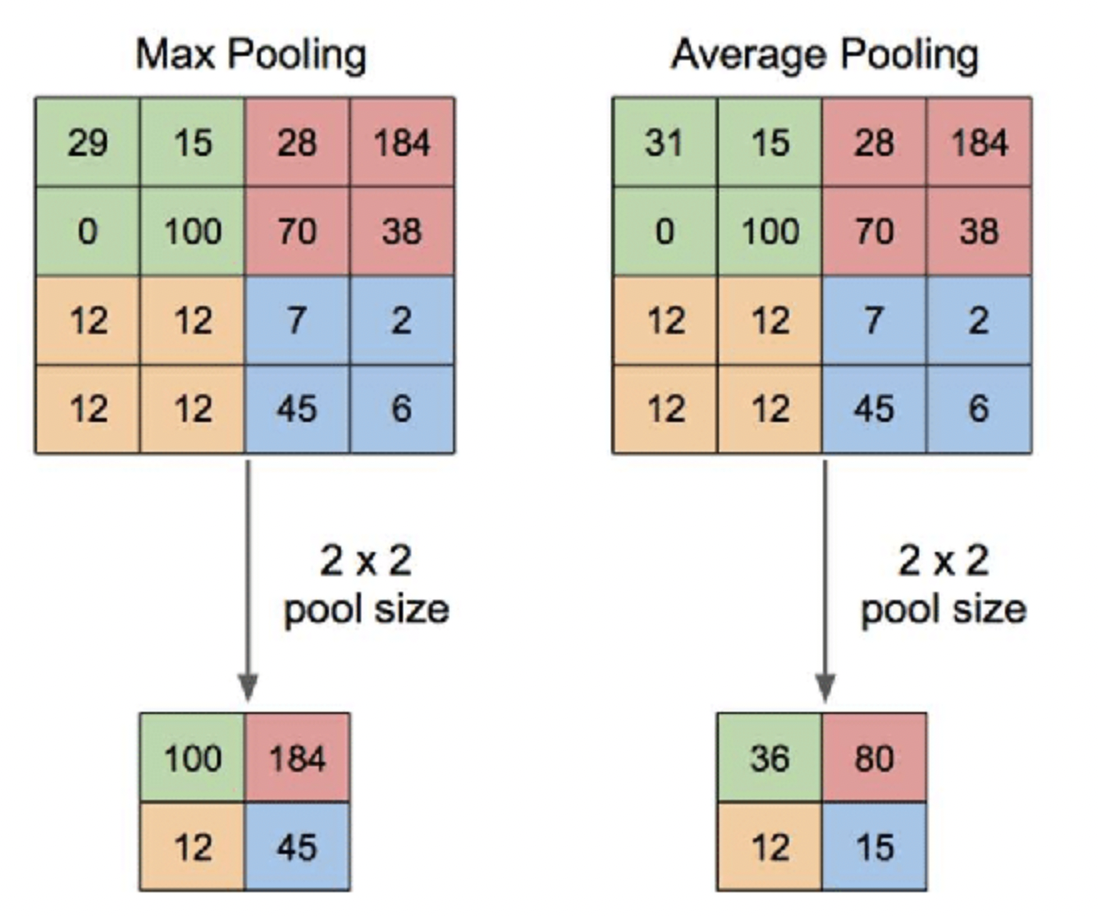
풀링층은 학습해야할 매개변수가 없고 채널 수가 변하지 않으며 강건(Robust)하기 때문에 입력 변화에 영향이 적음
Deep CNN
합성곱 신경망에서 층을 깊게 쌓으면 나오는 이점!
입력데이터와 가까운 쪽의 합성곱 층은 이미지의 극히 일부밖에 못본다!
하지만 층이 깊어지면 한번에 이미지의 많은 부분을 볼 수 있다!
풀링과정을 여러번 거치면서 많은 픽셀정보가 응축되서!!
CNN의 종류
AlexNet, GoogleNet, ResNet, VGG
수학
사건 A가 일어날 확률 -> P(A)
표본 원소가 n(s)이고 사건원소 A이면 -> P(A) = n(A)n(S)
임의의 사건 A가 일어날 확률은 0과 1 사이임
A가 반드시 일어나면 p(A) = 1
A가 절대 안일어나면 p(A)= 0
- 독립 사건과 종속사건
주머니 속에 흰색공 4개와 빨간 공 6개가 있을때 한번씩 꺼낼때 (다시 안넣음) => 독립 사건
주머니 속에 흰색공 4개와 빨간 공 6개가 있을때 한번씩 꺼낼때 (다시 넣음) => 종속 사건
조건부 확률
어떤 사건 A가 일어났다는 조건 하에 다른 사건 B가 일어날 확률 -> P(B|A)
ABC라는 고등학교에서 전체 학생 65%가 안경쓰고, 그 중 남학생이 안경쓴거 45%
임의로 뽑은게 안경이고 그 중 남학생일 확률
45/65 = 9/13
빈도 확률 VS 베이지안 확률
빈도 확률 -> 모든건 실험으로 직접 여러번 반복해야 알 수 있음!
베이지안 확률 -> 직접 해보지 않아도 주어진 정보들로 확률 표현 -> 가설 세우고 수정!
사후 확률(P(A|B)) = (우도확률P(B|A)x 사전 확률P(A) / 주변 우도P(B) )
사전확률은 결과가 나타나기 전에 결정된 원인 A의 확률
우도 확률 은 원인 A가 발생했다는 가정하에 결과 B가 발생할 확률
사후 확률: 결과 B가 발생했다는 가정하에 원인 A가 발생했을 확률
주변우도는 사건 B의 발현확률
한 학급에 학생 100명 여학생30%중 3%가 외국인 또 남학생 70%중 8%가 외국인 임의로 1명 외국인, 여학생일 확률

스팸메일 필터에서 베이지안 확률을 자주 사용! -> 메일 본문을 보고 추측!
행렬
전치 연산 -> 행과 열을 바꿈 X^T라고 함
1차원 ndarray에서는 어림도 없음!!
행과 열의 개수가 같은 행렬 -> 정방 행렬
대각행렬 - 대각선만 값이 있고 나머지는 0
np.diag([1,2,3]) -> (1 0 0 0 2 0 0 3 0)
항등 행렬 - np.identity(3) 이러면 대각만 1인 행렬!
대문자 I로 표시!
np.eye(3,5, k=1) 이러면 3,5 행렬에서 k부터 대각선으로 1임!
대칭 행렬 - 전치 행렬 했는데 원래 행렬과 같을 경우! 정방행렬만 대칭이 됨!
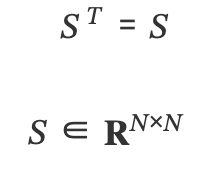
선형조합
벡터/행렬에 스칼라값을 곱하거나 더하거나 뺀거 -> 크기 변하지 않음!
벡터의 곱셈 - 내적!(inner product)
내적의 조건 -> 두벡터의 차원(길이)가 같아야하고, 앞의 벡터가 행이고 뒤가 열이어야함!
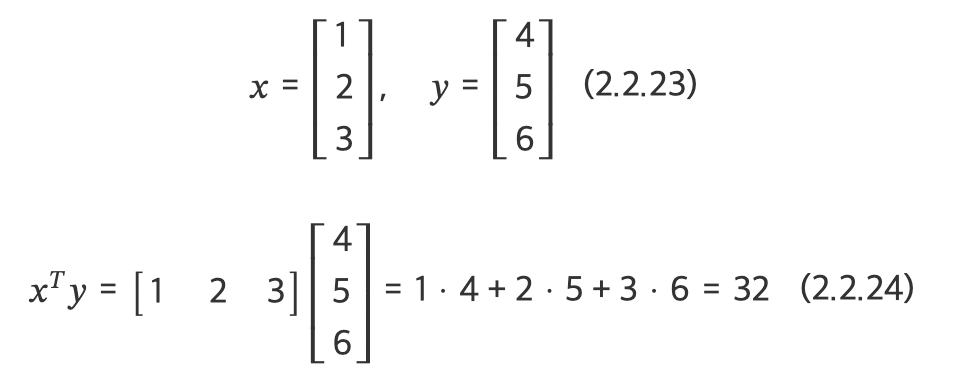
x = np.array( [ [1], [2], [3] ])
y = np.array( [ [4], [5], [6] ] )
x.T @ y # 또는 np.dot(x.T , y)
행렬 곱셉
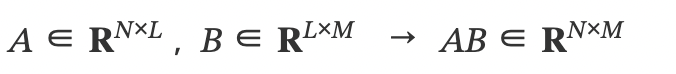
행렬 norm
모든 크기의 행렬에 대해서 정의할 수 있다!, 고로 벡터도 정의 가능!
np.linalg.norm(A,axis=1, ord=1)
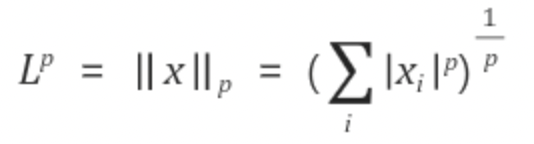
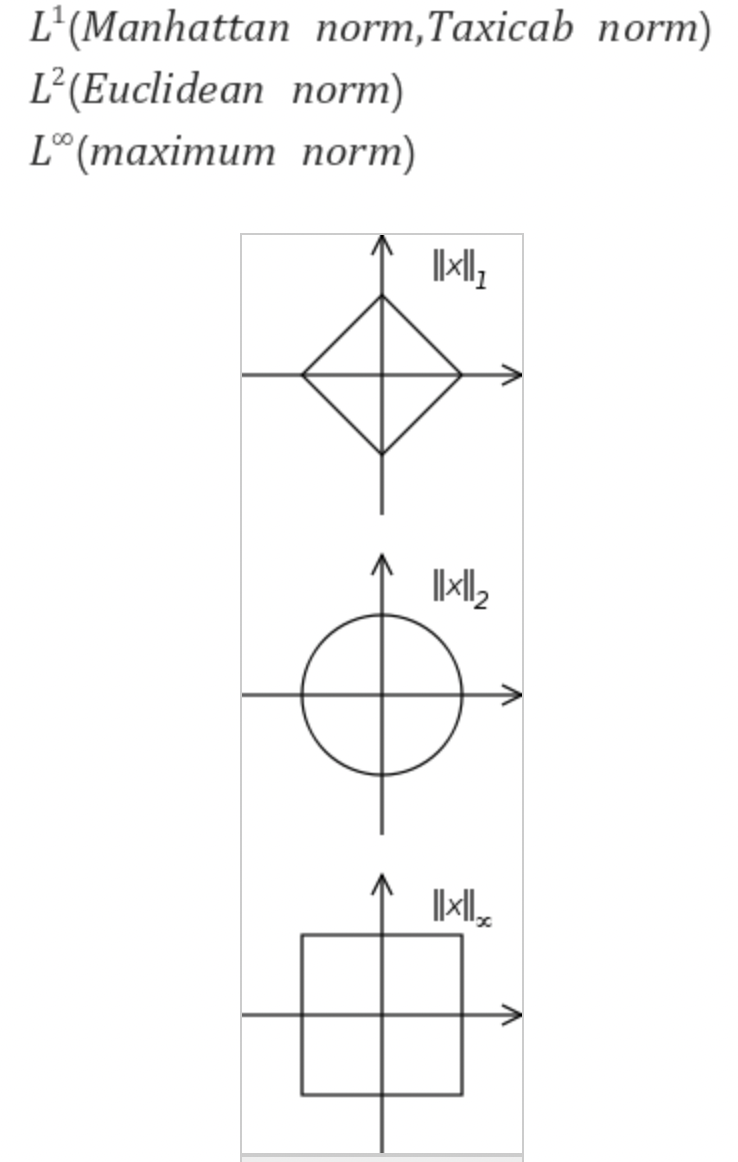
Norm1 - 절댓값을 취한뒤 전부 더한거!, 멘하탄 노름
Norm2 - 일단 제곱을 하고 전부 더한뒤 루트를 씌운거!, 유클리디안 노름
노름의 성질 3가지
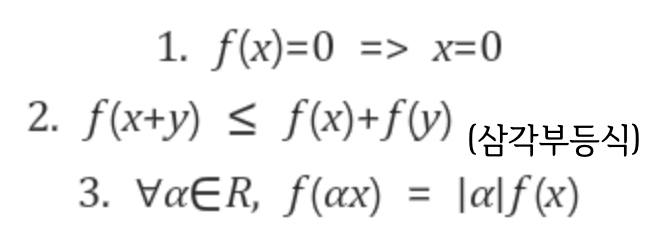
Precourse 관련 틀린 문제들 보며 부족한 부분 정리한 것들
딥러닝에서 OVerfiting을 해결하는 방법!
1. 더 많은 데이터를 사용!
2. Cross Validation
3. Regularization 사용!
파이썬 특징
플랫폼 독립적이고, 인터프리터 언어이고, 객체 지향이고, 동적타이핑임
함수 안에서 함수 밖 변수를 조작해도 당연히 함수 밖 변수한테는 영향이 없다!
a,b, c = [1,2,3,4,5,6] c가 남은거 다 가짐!
a = 10
float(a)
print(type(a)) # 이렇게 해도 type은 int다!!! 이거 왜? 10이어서 그런건가?
a = 10
b= float(a)
print(type(b)) # 이때 b는 float!! 즉 위는 a 자체가 영향을 받지는 않은거!!
파이썬 클래스에서 private는 변수에 f 처럼 앞에 붙이기!
OOP개념에서 필요한 요소들
inheritance,
polymorphism(같은 형태의 코드가 서로 다른 동작, 상속하고도 부모만 고치면 자식 수정),
visibility
CSV파일 읽을때 사용하는 CSV모듈은 파일 입력 파트 제외하고 4개의 attribute
delimeter, lineterminator
quotechar, quoting
정규 표현식
이거는 보다가 정리해놓으면 좋을거 같아서 정리해 두려고 한다!
“blue” [abc] 와 b가 일치하므로 매치!
[] 사이의 문자들과 매치!
[0-5] 는 12345를 의미
[a-zA-Z], [0-9]
^는 not이라는 의미를 같는다! [^0-9]라고 한다면 0-9가 아닌것만 매치!
\d - 숫자와 매치 [0-9]
\D - [^0-9]
\s - whitespace문자와 매치 [ \t\n\r\f\v]랑 동일
\S - whitespace가 아닌 것과 매치 [^ \t\n\r\f\v]
\w - [a-zA-Z0-9_]
\W [^a-zA-Z0-9_]
a.b는 a + 모든 문자 + b, 하나라도 있어야함!!, 줄바꿈 문자는 제외인듯
a[.]b이건 그냥 a.b임!
반복
ca*t
앞에 있는 a가 0부터 무한대로 반복 가능! -> ct, caaaat 도 가능!
ca+t는 1번이상 a가 나와야함!
ca{2}t는 a를 두번만 반복!
ca{2,5}t는 2부터 5회 반복 , caaaat 가능!
ab?c 는 {0,1}과 같은 의미!
- import re 를 사용하면 정규 표현식 가능!
확률
이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링한다. => yes!!
연속형 확률변수의 한 지점에서의 밀도 (density) 는 그 자체로 확률값을 가진다. => NO!!
각 면이 나올 확률이 균등하고 독립적인 정육면체 주사위를 던진다고 하자. 확률변수 X
X 는 주사위의 각 면의 숫자를 나타낸다고 할 때 ( X \in {1, 2, 3, 4, 5, 6} X∈{1,2,3,4,5,6} ),
X 의 기대값을 구하시오 (소수점 첫째자리까지 입력).
=> 이거는 걍 (1+2+3+4+5+6 ) / 6 하면 됨
표본 X 가 있을 때, X 의 평균 X={1,2,3,4,5} => (1+2+3+4+5) / 5
셀프 피드백
분산 관련 문제들 풀어보기
프로그래머스 더 다양하게 풀어보기
AI기초 수학 부분인 벡터 부분 (선형 독립 선형 종속 부분) 풀어보기