머신러닝 분석 개요

1. 머신러닝 개요

인공지능, 머신러닝, 딥러닝

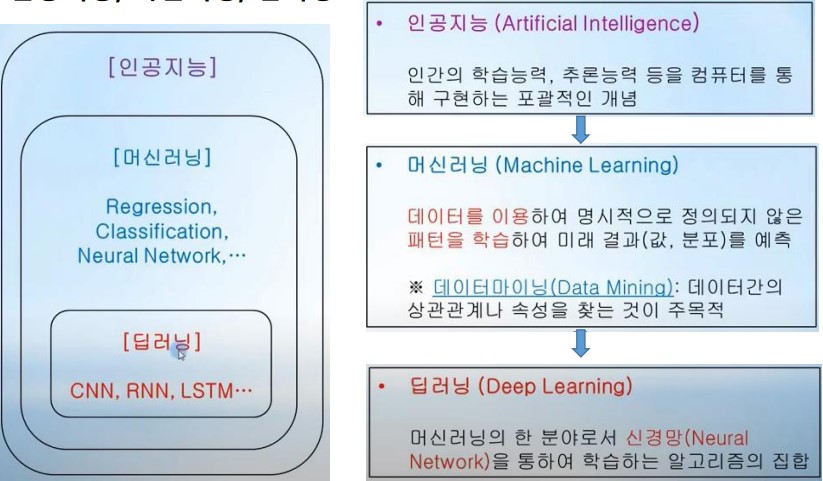
머신러닝 정의

• 머신러닝은 데이터에서부터 학습하도록 컴퓨터를 프로그래밍하는 과학(또는 예술)입니다.
• [아서 새뮤얼(Arthur Samuel), 1959] : “머신러닝은 명시적인 프로그래밍 없이 컴퓨터가 학습하는 능력을 갖추게 하는 연구 분야”
• [톰 미첼(Tom Mitchell), 1997] : “어떤 작업 T에 대한 컴퓨터 프로그램의 성능을 P로 측정했을 때 경험 E로 인해 성능이 향상됐다면, 이 컴퓨터 프로그램은 작업 T와 성능 측정 P에 대해 경험 E로 학습한 것”

머신러닝?

• 데이터에서 법칙성을 추출하는 통계적 방법’의 하나입니다.
• 법칙을 추출하여 예측, 분류하는 다양한 모델(알고리즘)입니다.
• 손글씨 문자 식별, 물체 식별, 질병 진단 등 다양한 분야에 걸쳐 응용됩니다.
• 딥러닝도 머신러닝의 일부로, 신경망 모델의 한 형태입니다.

머신러닝 문제의 분류

지도 학습 Supervised Learning 문제

• 입력에 대한 적절한 출력을 구하는 문제
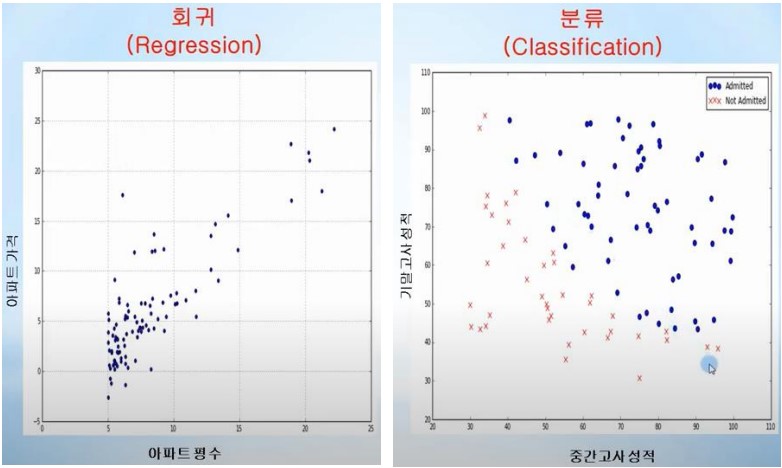
• Regression, Classification

비지도 학습Unsupervised Learning 문제

• 비지도 학습은 입력 정보의 특징을 찾는 문제
• Clustering

강화 학습 문제

• 강화 학습은 장기나 체스와 같이 마지막 결과가 가장 좋은 행동을 찾는 문제

Regression, Classification

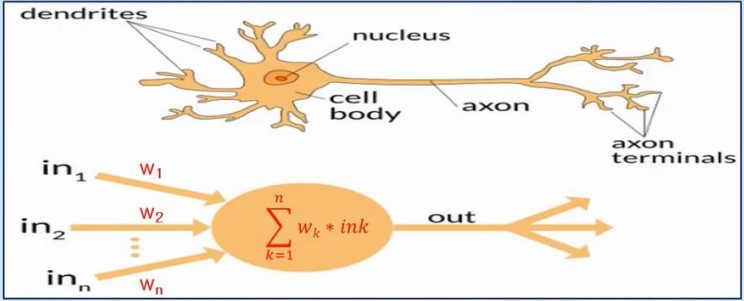
딥러닝 – Neural Networ

• 신경망(Neural Network) 인간의 뇌 세포(Neuron) 상호작용을 모방했습니다.
• 이전 뉴런 츨력을 각각의 입력으로 받아, + 또는 –가중치를 통해 전체 합을 합하여 특정 임계치(threshold)를 넘으면 다음 뉴런으로 전달하는 원리입니다.
  

머신러닝 / 딥러닝 구현 - 프레워크

2. 머신러닝 수학

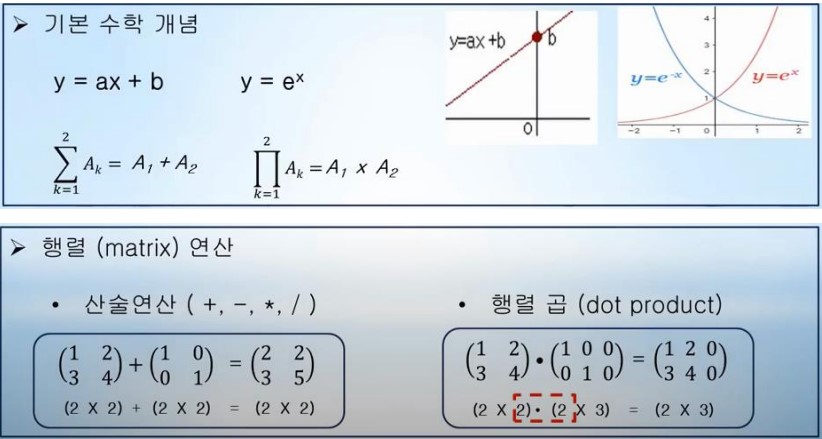
미분 - derivative

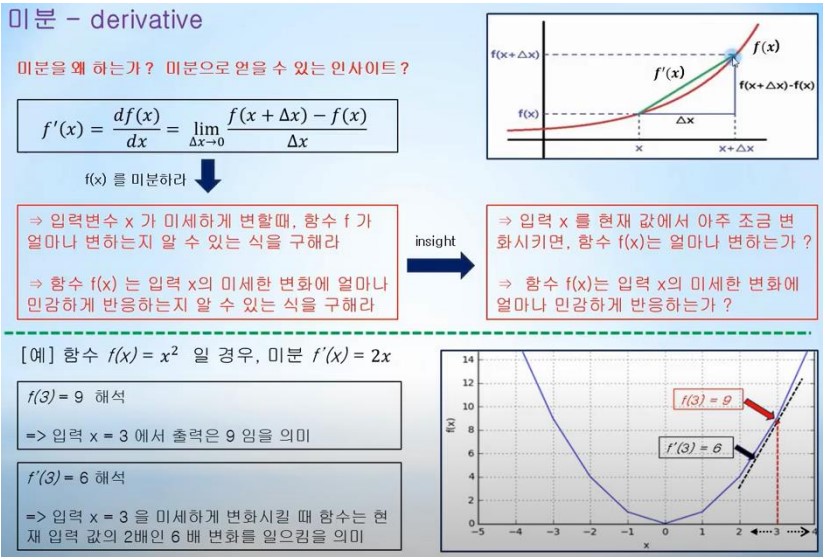
머신러닝 / 딥러닝에 자주 사용되는 함수 미분

편미분 - partial derivative

• 입력 변수가 하나 이상인 다 변수 함수에서 미분하고자하는 변수 하나를 제외한 나머지 변수들을 상수로 취급하고 해당 변수를 미분하는 것입니다.
• 예를 들어 f(x, y)를 변수 x에 대해 편미분 하는 경우 다음과 같이 나타냅니다.
  

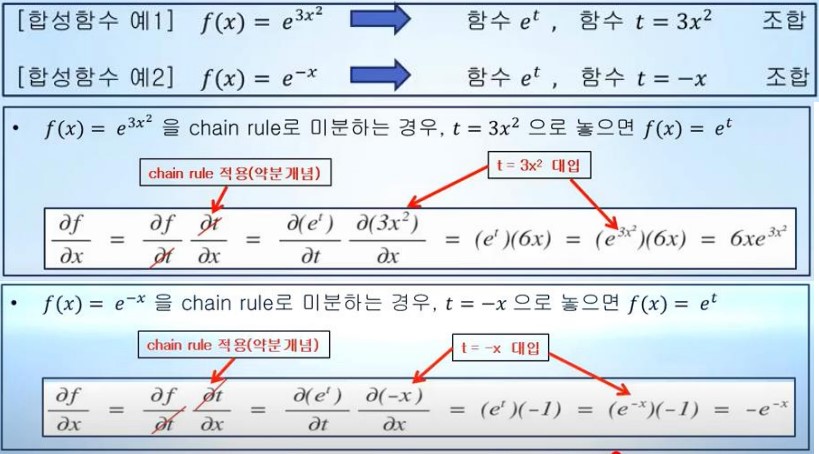
연쇄법칙 - chain rule

• 합성함수란 여러 함수로 구성된 함수로서 이러한 합성함수를 미분하려면 ‘함성함수를 구성하는 각 함수를 미분의 곱＇으로 나타내는 chain rule(연쇄법칙을 이용)
  

수치미분 1차 버전 - numerical derivative

• 수치미분은 주어진 입력 값이 미세하게 변할 때 함수 값 f는 얼마나 변하는지를 계산하는 것입니다.
  

수치미분 - 다변수

• 입력 변수가 하나 이상인 다 변수 함수의 경우 입력 변수는 서로 독립적이기 때문에 수치미분 또한 변수의 개수 만큼 개별적으로 계산하여야 합니다.
  

# 다변수 함수, 모든변수를 포함하고 있는 numpy객체(배열, 행렬…)
def numerical_derivative(f, x): # 수치미분 debug version
  delta_x = 1e-4
  # 계산된 수치미분 값 저장 변수
  grad = np.zeros_like(x)
  
  # 모든 입력변수에 대해 편미분하기 위해 iterator 획득
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  
  while not it.finished:
    idx = it.multi_index
    
    # Numpy 타입은 mutable이므로 원래 값 보관
    tmp_val = x[idx]
    # 하나의 변수에 대한 수치미분 계산
    x[idx] = float(tmp_val) + delta_x
    fx1 = f(x) # f(x+delta_x)
    x[idx] = tmp_val - delta_x
    fx2 = f(x) # f(x-delta_x)
    grad[idx] = (fx1 - fx2) / (2*delta_x)
    x[idx] = tmp_val
    it.iternext()
  return grad