3주차

3주차에서는 딥러닝의 기초 개념과 그것을 실습에 적용해보는 것으로 학습이 이뤄졌다. 여기서 딥러닝의 기초 개념은 tf의 api부터 시작해서 regularization 등등 아주 복합적이고 포괄적인 것을 의미한다.
뿐만 아니라 머신러닝, 딥러닝의 학습에 대해 fundamental하게 공부하는 시간이 되었다. 보다 자세한 내용은 목차에서 확인하는 걸로 하자! 보다 자세한 개념을 위해 따로 시간을 내야할 것 같다.

3주차 학습 목차

3주차 학습 목차는 다음과 같다.
너무 방대한 내용을 다루기 때문에 하나하나 자세하게 이해하는 데에 많은 시간이 걸렸다. 따라서 각 내용을 개괄적으로 다루도록 하고, 1~5까지는 이번 포스팅에서, 6~10까지는 다음 포스팅에서 다루도록 하겠다.

1. 넘파이로 구현하는 딥러닝

2. CNN 기반 다양한 모델의 특징

3. 활성화 함수의 이해

4. regularization

5. regression - linear / logistic

6. 확률과 확률분포

7. likelihood와 MLE

8. 정보이론(information theory)

9. 비지도 학습(unsupervised learning)

10. 추천 시스템 기초 with sklearn

1. 넘파이로 구현하는 딥러닝

딥러닝 api를 사용하는 것이 아니라 파이썬의 넘파이를 사용하여 딥러닝의 학습 방법에 대해 이해할 수 있었다.
중요한 것은 딥러닝의 학습 방식을 파악하는 것과 어떤 모듈을 만들어서 신경망을 학습시킬지 생각해보는 것이다.

전체적으로 신경망을 학습시키기 위해 활성화 함수와 손실 함수를 정의하고 모델에 데이터를 학습시킨다. 모델이 예상한 값과 실제 값을 비교하면서 손실함수를 작게하는 파라미터를 추정하면서 모델에 학습이 이뤄진다.
이 때 경사하강법과 오차역전파 기법이 사용된다. 이러한 전체적인 모델의 학습 방식에 대해 그림을 그릴 줄 알면서 이를 파이썬 코드로 작성하는 챕터였다.

전체적인 코드는 다음과 같다. 데이터는 mnist dataset을 활용!!

import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt

# mnist를 불러오고 train_data, train_label, test_data, test_label로 나눠주세요.
mnist = keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()  

#우리의 모델은 MLP이기 때문에 데이터를 255로 나누고 1차원(60000, n)으로 만들어주세요.
x_train_norm, x_test_norm = x_train / 255.0, x_test /255.0
x_train_reshaped = x_train_norm.reshape(60000, -1)
x_test_reshaped = x_test_norm.reshape(10000, -1)

# 초기화된 파라미터를 정의하는 함수를 만들고 초기값을 만드세요.
def init_params(input_size, hidden_size, output_size, weight_init_std=0.01):
    #W1, b1, W2, b2를 모두 정의해주세요.
    W1 = weight_init_std * np.random.randn(input_size, hidden_size)
    b1 = np.zeros(hidden_size)
    W2 = weight_init_std * np.random.randn(hidden_size, output_size)
    b2 = np.zeros(output_size)
    
    return W1, b1, W2, b2

W1, b1, W2, b2 = init_params(input_size = 728, hidden_size = 50, output_size = 10)

# MLP를 정의하세요.
def affine_layer_forward(X, W, b):
  y = np.dot(X, W) + b
  cache = (X,W,b)
  return y, cache

# relu를 정의하세요 (np.maximum을 활용하세요)
def relu(x):
  result = np.maximum(0, x)
  return result

# softmax를 정의하세요
def softmax(x):
  if x.ndim == 2:
    x = x.T
    x = x - np.max(x, axis=0)
    y = np.exp(x) / np.sum(np.exp(x), axis=0)
    return y.T 

  x = x - np.max(x) # 오버플로 대책
  return np.exp(x) / np.sum(np.exp(x))
  
  # one-hot 인코딩을 정의하세요
def _change_one_hot_label(X, num_category):
    T = np.zeros((X.size, num_category))
    for idx, row in enumerate(T):
      row[X[idx]] = 1
    return T

# cross entropy loss함수를 정의하세요
def cross_entropy_error(y, t):
  if y.ndim == 1:
    t = t.reshape(1, t.size)
    y = y.reshape(1, y.size)
  if t.size == y.size:
    t = t.argmax(axis = 1)

  batch_size = y.shape[0]
  result = -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size
  return result

# MLP의 backward pass를 정의하세요
def affine_layer_backward(dy, cache):
  X, W, b = cache
  dX = np.dot(dy, W.T)
  dW = np.dot(X.T, dy)
  db = np.sum(dy, axis = 0)
  return dX, dW, db

# relu 함수의 backward pass를 정의하세요. (np.where 함수를 활용하세요)
def relu_grad(x):
  return np.where(x>0, 1, 0)

#파라미터를 업데이트하는 함수를 정의하세요.
def update_params(W1, b1, W2, b2, dW1, db1, dW2, db2, learning_rate):
  W1 = W1 - learning_rate * dW1
  W2 = W2 - learning_rate * dW2
  b1 = b1 - learning_rate * db1
  b2 = b2 - learning_rate * db2

  return W1, b1, W2, b2
  
  # train_step을 정의합니다.
def train_step(X, Y, W1, b1, W2, b2, learning_rate=0.1, verbose=False):
  a1, cache1 = affine_layer_forward(X, W1, b1)
  z1 = relu(a1)
  a2, cache2 = affine_layer_forward(z1, W2, b2)
  y_hat = softmax(a2)
  t = _change_one_hot_label(Y, 10)
  Loss = cross_entropy_error(y_hat, t)


  if verbose:
      print('---------')
      print(y_hat)
      print(t)
      print('Loss: ', Loss)

  dy = (y_hat - t) / X.shape[0]
  dz1, dW2, db2 = affine_layer_backward(dy, cache2) #dz1=(5,784) a1 = (100,50)
  da1 = dz1 * relu_grad(a1) 
  dX, dW1, db1 = affine_layer_backward(da1, cache1)

  #파라미터 갱신  
  W1, b1, W2, b2 = update_params(W1, b1, W2, b2, dW1, db1, dW2, db2, learning_rate)
  return W1, b1, W2, b2, Loss

# 예측값을 만드는 함수를 정의하세요
def predict(W1, b1, W2, b2, X):
  a1 = np.dot(X,W1) + b1
  z1 = relu(a1)
  a2 = np.dot(z1, W2) + b2
  y = softmax(a2)
  return y

#정확도를 나타내는 함수를 정의하세요
def accuracy(W1, b1, W2, b2, x, y):
  y_hat = predict(W1, b1, W2, b2, x)
  y_hat = np.argmax(y_hat, axis=1)
  # t = np.argmax(t, axis=1)

  accuracy = np.sum(y_hat == y) / float(x.shape[0])
  return accuracy

# 하이퍼파라미터
iters_num = 50000  # 반복 횟수를 적절히 설정한다.
train_size = x_train.shape[0]
batch_size = 100   # 미니배치 크기
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

# 1에폭당 반복 수
iter_per_epoch = max(train_size / batch_size, 1)

W1, b1, W2, b2 = init_params(784, 50, 10)

for i in range(iters_num):
  # 미니배치 획득
  batch_mask = np.random.choice(train_size, batch_size)
  x_batch = x_train_reshaped[batch_mask]
  y_batch = y_train[batch_mask]
  

  W1, b1, W2, b2, Loss = train_step(x_batch, y_batch, W1, b1, W2, b2, learning_rate=0.1, verbose=False)

  # 학습 경과 기록
  train_loss_list.append(Loss)
  
  # 1에폭당 정확도 계산
  # train_accuracy와 test_accuracy를 완성해주세요
  if i % iter_per_epoch == 0:
      print('Loss: ', Loss)
      train_acc = accuracy(W1, b1, W2, b2, x_train_reshaped, y_train)
      test_acc = accuracy(W1, b1, W2, b2, x_test_reshaped, y_test)
      train_acc_list.append(train_acc)
      test_acc_list.append(test_acc)
      print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 12, 6 

# Accuracy 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

# Loss 그래프 그리기
x = np.arange(len(train_loss_list))
plt.plot(x, train_loss_list, label='train acc')
plt.xlabel("epochs")
plt.ylabel("Loss")
plt.ylim(0, 3.0)
plt.legend(loc='best')
plt.show()

2. CNN 기반 다양한 모델의 특징

computer vision(cv)분야에서 주로 사용되는 Convolutional Neural Network의 주요 개념 및 널리 사용되는 VGG, ResNet 등 네트워크 구조에 대해 알아보는 챕터였다.
이번 챕터에서 느낀 점은 CNN기반 모델 아키텍쳐를 구성할 때, 혹은 분석할 때 모델의 각 층에서의 input, output shape을 파악하는 것이 중요하다는 것이다. 이를 습관화하도록 하고, VGG와 ResNet의 특징을 알아보자.

• VGG : VGG는 AlexNet 같이 이미지넷 챌린지에서 공개된 모델로, 이 모델은 2014년 이미지넷 챌린지 준우승을 거뒀다.

이전에 우승한 네트워크들이 10개가 안 되는 CNN층을 가진 반면, VGG16과 VGG19라는 이름 뒤의 숫자로 볼 수 있듯이, VGG는 16개, 19개의 층으로 이뤄진다.

그럼 VGG에서는 어떤 방식으로 이런 레이어를 쌓았을까?
CNN을 만들 때 우리는 커널 크기(kernel size)를 조절한다. VGG에서는 3x3 커널을 사용해서 더 많은 레이어를 쌓고 이미지의 비선형적 특성을 더 잘 잡아낼 수 있게 만들었다.
즉, 커널의 크기를 크게, 적게 쌓는 방식이 아니라 작게, 여러번 쌓아 더욱 효율적인 모델 학습이 가능하게 하는 것이다.

예를 들어, 5x5 filter와 3x3 filter를 비교하면서 설명해보자.
만일 우리가 28x28x1 이미지에 5x5 filter로 convolution 연산을 하게 된다면 output은 24x24x1 이미지로 출력된다.
(24가 나오는 이유는 (input image size-filter size)/stride+1)로 계산되기 때문이다.)

그렇다면 3x3 filter로 convolution 연산을 2번 하면 어떻게 될까? 계산해보면 28x28x1이미지가 26x26x1 이미지로 변하고 26x26x1 이미지가 24x24x1 이미지로 변화한다.
즉 5x5 filter를 1번 사용했을 때 receptive field의 크기와 3x3 filter를 2번 사용했을 때의 크기는 서로 같다고 볼 수 있다.

그렇다면 parameter의 개수를 직접 구해보면 어떤 값이 나올까?
parameter의 경우에는 filter size x filter size x channel로 구한다. 위에 있는 예시에서, 5x5 filter를 1번 쓴 convolution 연산은 5x5x1 = 25개의 parameter가 필요하다.
한편 3x3 filter를 2번을 쓴 convolution 연산은 2x3x3x1 = 18개의 parameter가 필요하다.

-> 결과적으로 3x3 convolution 연산을 2번 했을 때, 5x5 filter로 연산을 1번 했을 때와 receptive field의 크기는 같지만 parameter 수의 차이를 고려하면 더 효율적이라 볼 수 있다.

-> 하지만 모델이 깊어질 수록 여전히 vanishing gradient문제가 발생한다.

-> 이를 해결하고자(기울기 소실 문제를 해결) 나타난 모델이 ResNet모델

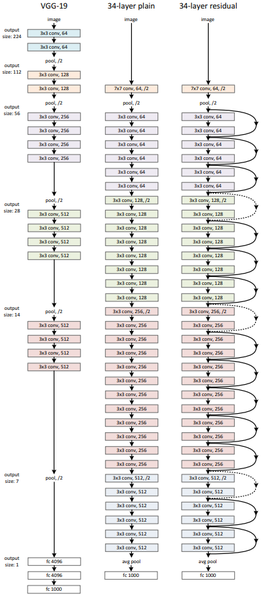
• ResNet: 위 그림에서 알 수 있듯이 vgg에 비해 더욱 깊은 레이어를 가지고 있지만 residual층으로 skip connection을 활용하여 vanishing gradient문제를 해결하는 데에 사용했다.

skip connection의 활용은 다음 그림을 보면 이해하기 쉽다.

Layer를 통과한 파라미터(F(x))에 원래 입력 (X)를 더해주는 것이다. 이 과정을 단위로 한 블럭을 residual block이라고 부르는 것이다.
이 블럭에서 오차 역전파를 진행하면 어떻게 vanishing gradient문제를 해결하려고 하는지 알 수 있다.

f(x) + x를 x에 대해 미분한다고 해보자. f(x)를 x에 대한 미분을 한 값에 1을 더하는 것과 같다. 레이어가 깊어지면서 기울기가 0~1사이의 값이 나오더라도 1을 더해줌으로써 미미해진 기울기를 어느정도 끌어 올리는 역할을 하는 것이다.(개인적으로는 RNN의 되먹임 구조가 생각났다.)
그럼 vgg + resnet의 특성을 이용하면 되는 것 아닌가?? 물론 그런 모델이 있을 것이다.

3. 활성화 함수의 이해

신경망 딥러닝 모델에서 활성화 함수를 사용하는 이유는 무엇일까?
바로 선형적으로 연결된 (fully connected layer) 공간을 비선형적 공간으로 변형시키기 위함이다.
그래서 파라미터 공간을 비선형적으로 바꾸면 뭐가 좋은데!?
정답은 "모델의 표현력이 향상된다" 이다.
그 이유는 선형적 layer를 계속 쌓는다고 하여도 결국 선형적 layer하나와 같은 역할로 귀결되기 떄문이다.

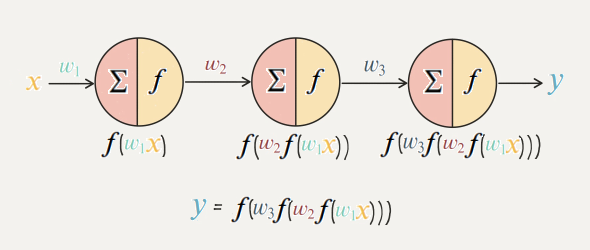
즉, 선형레이어를 계속 쌓아도 별 효과가 없으니 활성화 함수를 사용하여 모델의 표현력을 향상시키자!

-활성화 함수의 종류
자주 사용되고 이해하기 편한 활성화 함수의 종류는 다음과 같다.

1. 이진계단 함수
2. relu함수
3. sigmoid, softmax함수
4. 하이퍼볼릭 탄젠트 함수(tanh)
   등등 ..

활성화 함수에 대한 간단한 내용은 아래의 포스팅에서 확인해보고 넘어가자!
활성화 함수 참고 포스팅
ㄴ> 각 함수가 어떤 역할을 하고 어떤 task에서 자주 사용되는 지 알면 된다고 생각한다!

4. regularization

Regularization과 Normalization은 한국어로 번역하면 정규화라고 겹쳐서 표현되는 경우가 많다.
따라서 각 개념을 알 필요가 있고 앞으로는 의미가 헷갈리지 않도록 영어를 쓰도록 하자!

(1) Regularizaion : 오버피팅을 해결하기 위해 사용하는 방법 중 하나. 다양한 종류가 있지만 L1, L2 regularization / dropout / batch normalizaion 등의 기법이 유명하다.

(2) Normalizaion : 모델에 학습시킬 데이터를 보다 의미있고, 학습에 적합하도록 전처리하는 과정을 의미한다. 가령 데이터의 scale이 달라 z-score로 바꾸거나, minmax scaler를 사용하는 등 데이터의 분포가 피처값의 범위에 의해 왜곡되지 않도록 하는 과정이다.

이 중 regularization 기법에 대해 공부했다 !
1. L1 / L2 regularizaion
2. dropout
3. batch normalizaion
(각각이 중요한 개념이기 때문에 추후에 블로그에 따로 업로드할 예정!)

5. regression - linear / logistic

Regression(회귀)란?
회귀 분석이라고도 부르며, 관찰된 데이터를 기반으로 각 연속형 변수 간의 관계를 모델링하고 이에 대한 적합도를 측정하는 분석 방법을 의미한다.
즉, 독립변수(independent variable)와 종속변수(dependent variable) 사이의 상호 관련성을 규명하는 것이다.

아래의 그림은 Galton이 분석했던 아버지의 키와 자식의 키 사이의 관계에 대한 원본 데이터와 이를 토대로 그려본 직선 형태의 함수 관계도인데, 이를 회귀분석이라고 할 수 있다.

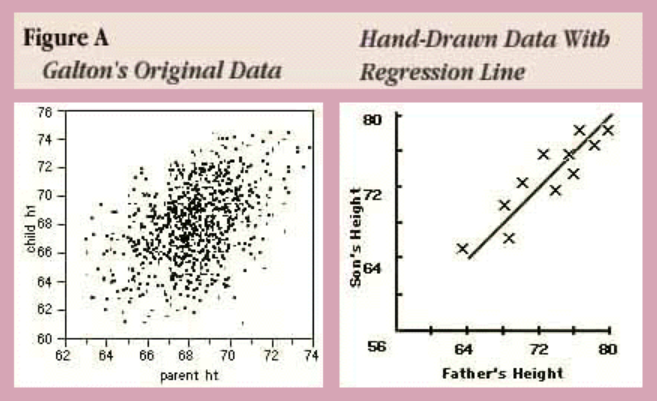
출처 : http://www.biostat.jhsph.edu/courses/bio653/misc/JMPer%20Cable%20Summer%2098%20Why%20is%20it%20called%20Regression.htm

• Linear regression
  선형회귀의 독립변수가 하나면 단순 선형회귀, 두 개 이상이면 다중 선형회귀라고 부른다. (H = Wx + b)의 꼴
  만약 최소제곱법을 사용한다면, 잔차의 제곱의 합을 최소로하는 W,b값을 귀하는 방법을 의미한다!

• logistic regression
  데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해 주는 지도 학습 알고리즘이다.
  선형회귀분석과 비슷한데 , Y값이 확률로 되어 있기 때문에 하한, 상한이 [0, 1] 이다. 특정 threshold 기준으로 0과 1을 구분하기 때문에 이진 분류의 문제를 풀 때 많이 사용한다.

여기서 선형회귀 분석과 왜 비슷한지 궁금하다면 아래의 링크를 참고해볼것!
포스팅할 예정

간단하게 설명하면, log odds라는 것을 선형회귀 분석의 종속 변수처럼 사용하기 때문이다.
odds라는 개념에 log를 취해서 선형 회귀처럼 각 변수들의 값을 더해서 0 / 1에 속할 확률에 대해 정리하면 우리가 잘 아는 시그모이드 함수식과 같아지는 것이다!