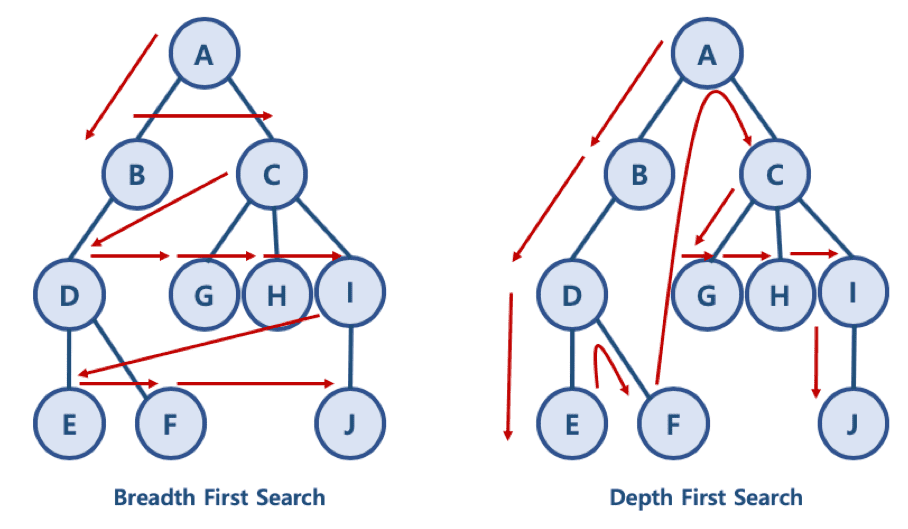
이진트리
-
비선형 자료구조이다
- 이진 탐색 트리(Binary Search Tree)
- 균형 이진 트리(Balanced Binary Search Tree)
- 다 방향 탐색 트리(Multi-Way Search Tree)
- 이진 힙
-
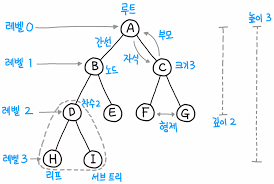
이진트리 용어
- 루트(Root) 노드 - 트리의 최상위에 있는 노드
- 자식(Child) 노드 - 노드 하위에 연결된 노드
- 부모(Parent) 노드 - 노드 상위에 연결된 노드
- 이파리(Leaf) 노드 - 자식 없는 노드
- 형제(Sibiling) 노드 - 동일한 부모를 가지는 노드
- 조상(Ancestor) 노드 - 루트까지 경로 위에 있는 노드
- 후손(Descendant) 노드 - 노드 아래에 매달린 모든 노드
- 서브 트리(Subtree) - 노드 자신과 후손으로 구성된 트리
- 레벨(Level) - 루트는 레벨 1, 아래 층으로 내려가며 1씩 증가
- 레벨은 깊이(Depth)와 동일 - 높이(Height) - 트리의 최대 레벨
- 키(Key) - 탐색에 사용되는 노드에 저장된 정보
-
포화 이진 트리
- 모든 이파리의 깊이가 같고 각 내부 노드가 2개의 자식을 가지는 트리
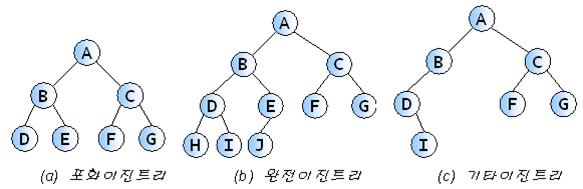
- 모든 이파리의 깊이가 같고 각 내부 노드가 2개의 자식을 가지는 트리
-
완전 이진 트리
- 마지막 레벨을 제외한 각 레벨의 노드로 꽉 차있고, 마지막 레벨에는 노드가 왼쪽부터 빠짐없이 채워진 트리
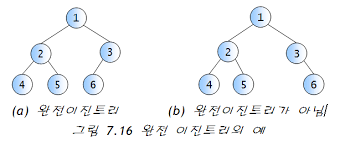
- 마지막 레벨을 제외한 각 레벨의 노드로 꽉 차있고, 마지막 레벨에는 노드가 왼쪽부터 빠짐없이 채워진 트리
-
편향 이진 트리
- 편향 이진 트리를 배열에 저장하는 경우, 트리의 높이가 커질수록 메모리 낭비가 매우 심각해진다.
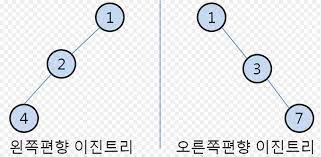
- 편향 이진 트리를 배열에 저장하는 경우, 트리의 높이가 커질수록 메모리 낭비가 매우 심각해진다.
이진 힙
-
우선순위 큐를 구현하는 가장 기본적인 자료구조
-
이진 합은 완전 이진 트리로서 부모의 우선순위가 자식의 우선순위보다 높은 자료구조이다.
-
우선순위 큐 (Parioty queue)
- 우선순위 개념 + 큐 자료구조
- 가장 높은 우선순위를 가진 항목에 접근,삭제와 임의의 우선수위를 가진 항목을 삽입을 지원하는 자료구조
- 이용 : 네트워크 트래픽 제어, 운영체제의 작업 스케줄링
-
스택이나 큐도 일종의 수선순위 큐
- 스택 : 후입 선출 자료구조 이므로 가장 마지막으로 삽입된 항목이 가장 높은 우선순위를 가진다.
- 큐 : 선입 선출 자료구조 이므로 먼저 삽입된 항목이 우선 순위가 더 높다.
-
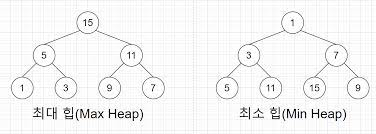
최소 힙 (minimum heap)
- 각 부모 노드의 값은 자기 자식 노드의 값보다 작다(힙의 속성)
- 키가 작을수록 높은 우선순위
- 루트 노드에는 최소값이 저장
-
최대 힙 (maximum heap)
- 각 부모 노드의 값은 자기 자식 노드의 값보다 크가(힙의 속성)
- 키가 클수록 더 높은 우선순위
- 루트 노드에는 최대값이 저장
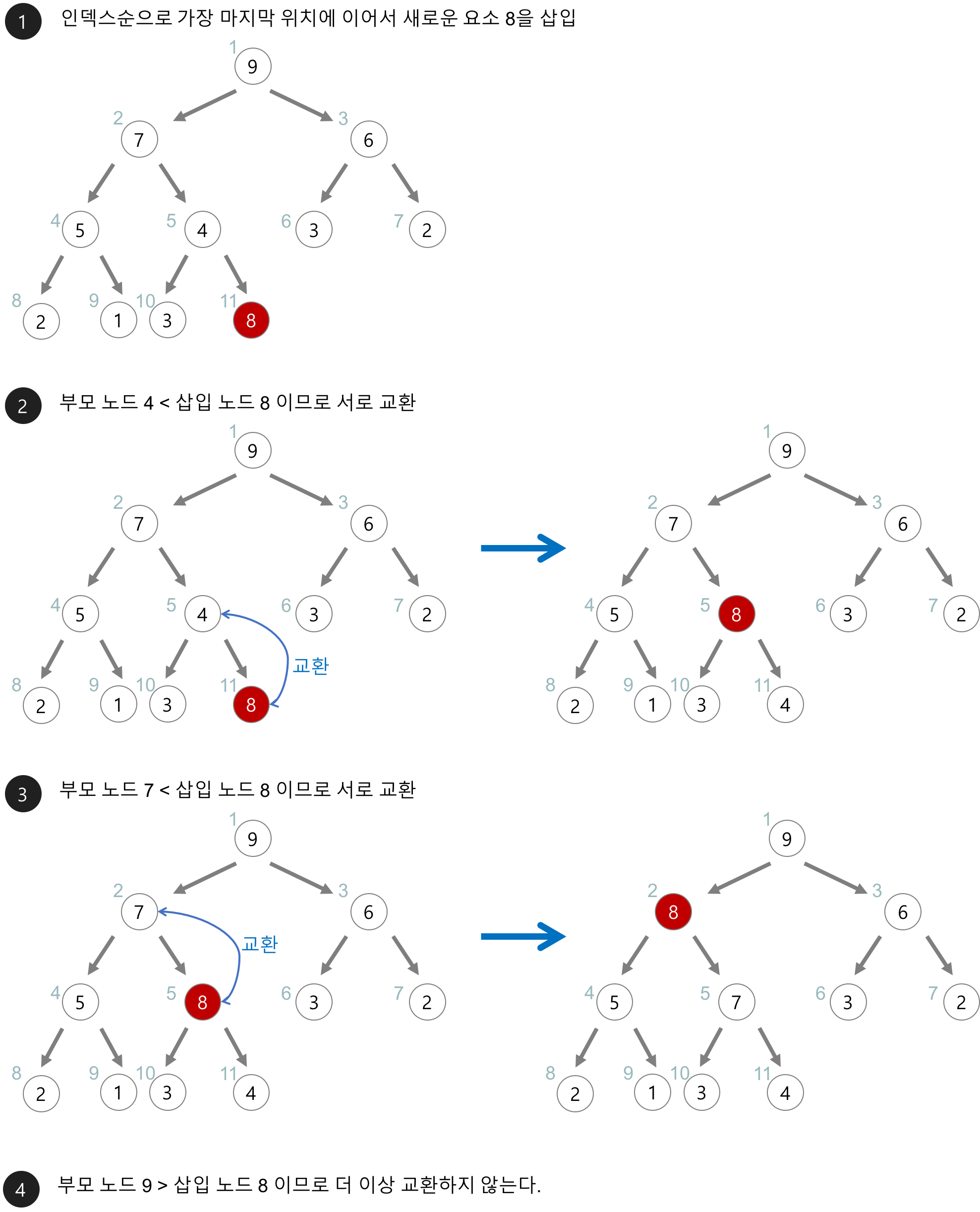
이진 힙의 삽입 연산 알고리즘
- 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
- 새로운 노드를 부모노드들과 비교 또는 교환 연산을 해서 힙의 성질을 만족시킨다.
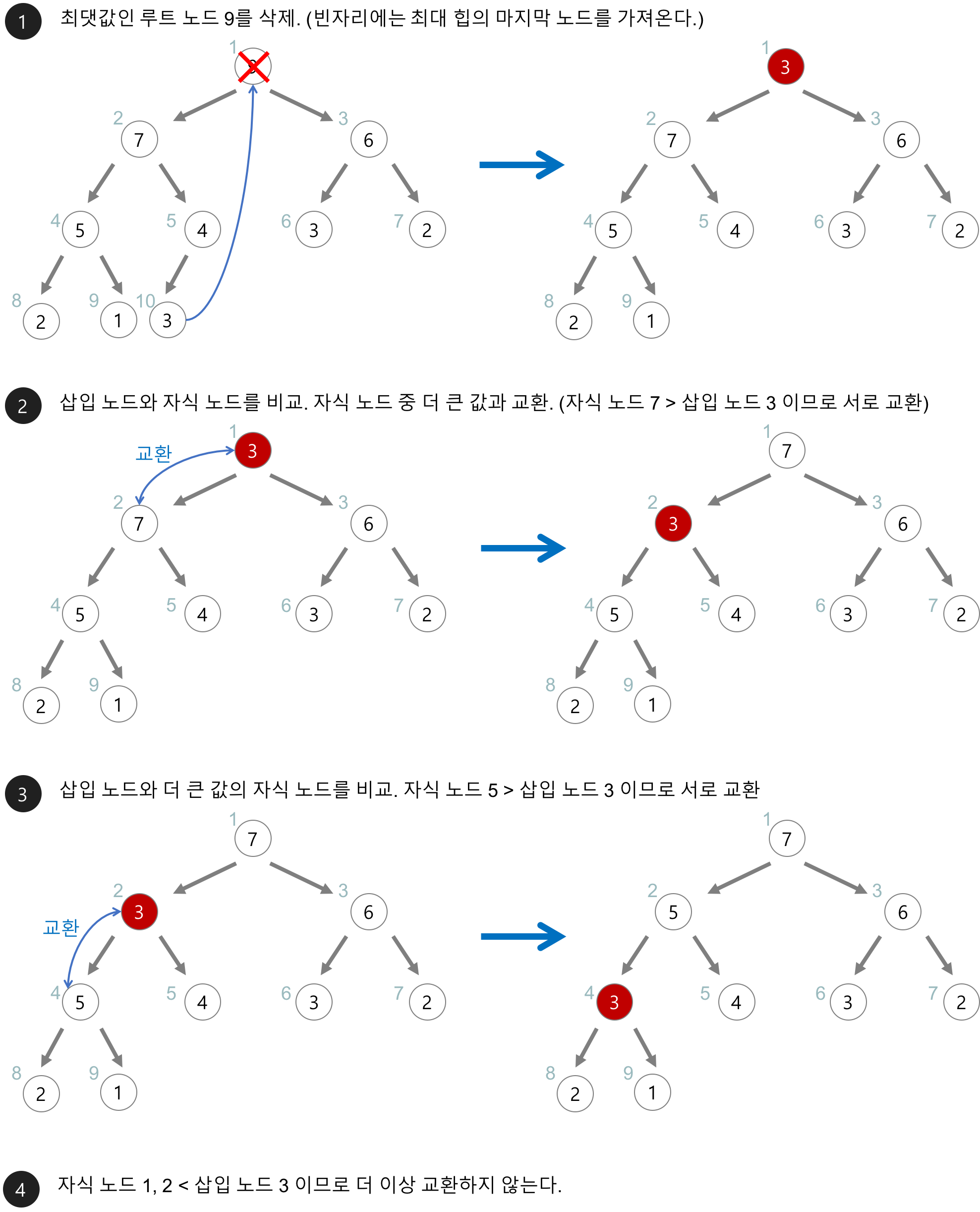
이진 힙의 삭제 연산 알고리즘
- 루트 노드를 삭제한다.
- 삭제된 루트 노드에는 힙의 마지막 노드를 삽입한다.
- 힙을 재구성한다.
-
삽입 노드와 자식 노드를 비교한다.
-
자식 노드와 삽입 노드를 교환.
파이썬 heapq 모듈로 힙 자료구조 사용
- heapq 모듈은은 완전 이진 트리 기반의 최소 힙 자료구조를 제공.
- min heap에서 가장 작은값은 언제나 인덱스 0, 즉, 이진 트리의 루트에 위치
- 내부적으로 min heap 내의 모든 원소(k)는 항상 자식 원소들(2k+1,2k+2) 보다 작거나 같도록 원소가 추가되고 삭제.
1. 힙 삽입 및 연산 구현
# 힙 원소 추가
# 40,20,15,35,45,10
from heapq import heappush
heap = []
heappush(heap,40)
heappush(heap,20)
heappush(heap,15)
heappush(heap,35)
heappush(heap,45)
heappush(heap,10)
print(heap) -> [10, 35, 15, 40, 45, 20]
# 힙 원소 삭제
heappop(heap)
print(heap) -> [15, 35, 20, 40, 45]
# 기존 리스트를 힙으로 변환
from heapq import heapify
list = [40,10,20,50,70]
heapify(list)
print(list) -> [10, 40, 20, 50, 70]2. 힙 정렬 구현
import heapq
a = [54, 88, 77, 26, 93, 17, 49, 10, 11, 31, 22, 44, 20]
print('정렬 전:\t', a)
heapq.heapify(a) ## 최소 힙으로 변환
print('힙:\t', a)
s = []
while a: ## 오름차순 정렬 과정
s.append(heapq.heappop(a)) ## 반복문을 통해 최소 힙 루트에 있는 루트(최솟값)를 반복적으로 리스트에 저장
print('정렬 후:\t', s)
* 결과 *
정렬 전: [54, 88, 77, 26, 93, 17, 49, 10, 11, 31, 22, 44, 20]
힙: [10, 11, 17, 26, 22, 20, 49, 54, 88, 31, 93, 44, 77]
정렬 후: [10, 11, 17, 20, 22, 26, 31, 44, 49, 54, 77, 88, 93]그래프
-
그래프는 정점(Vertex)과 간선(Edge)의 집합
- 하나의 간선은 2개의 정점을 연결
-
G=(V,E)로 표현, V= 정점의 집합, E= 간선의 집합
-
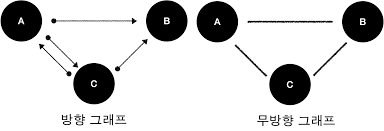
그래프의 종류
- 무방향 그래프 : 간선에 방향이 없는 그래프
- 방향 그래프 : 간선에 방향이 있는 그래프
-
그래프 용어
- 정점 a와 b를 연결하는 간선:(a,b)
- 정점 a에서 b로 간선의 방향이 있는경우 <a,b>
- 차수 : 정점에 인접한 정점의 수 (진입차수, 진출차수)
- 가중치 그래프 : 간선에 가중치가 부여된 그래프 (거리,시간 ...)
- 부분 그래프 : 주어진 그래프의 정점과 간선의 일부분으로 이루어진 그래프
- 트리 : 사이클이 없는 그래프
- 신장 트리 : 주어진 그래프가 하나의 연결 성분으로 구성되어 있을 때, 그래프의 모든 정점을 사이클 없이 연결하는 부분 그래프
-
그래프 자료구조
- 인접 행렬(Adjacency Matrix)
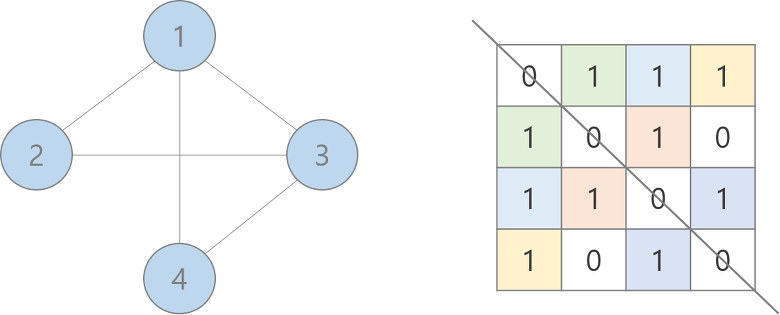
- 인접 리스트(Adjacency List)
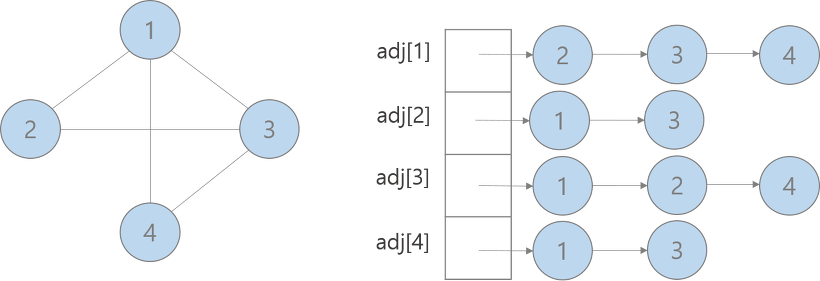
- 인접 행렬(Adjacency Matrix)
-
그래프 구현
- DFS 깊이 우선 탐색
- BFS 넓이 우선 탐색
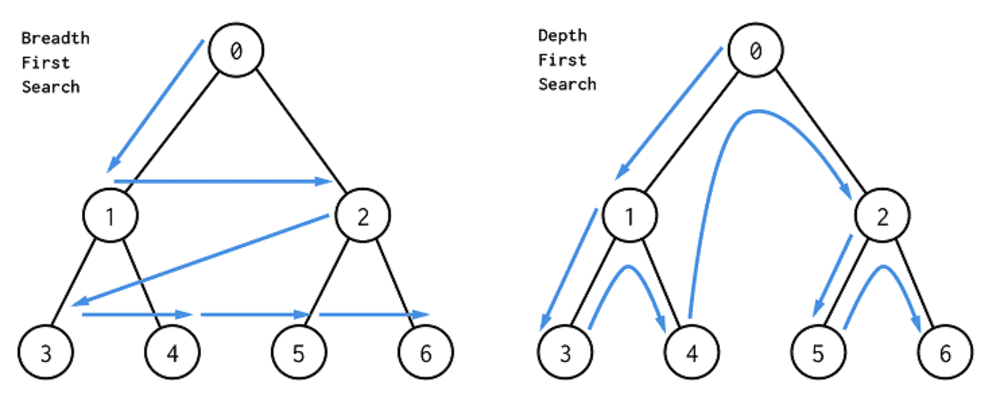
- DFS 그래프 순회 연산구현
- 스택을 사용하여 구현
- 재귀적 방법을 이용
adj_list = [[2, 1], [3, 0], [3, 0], [9, 8, 2, 1],
[5], [7, 6, 4], [7, 5], [6, 5], [3], [3]]
n = len(adj_list) # 그래프 정점 수
visited = [False for _ in range(n)] # 방문되면 True 로 (list comperhension)
# for loop 로 표현 가능
# visited = []
# for _ in range(n): #visted list 안에 방문표시 false 값으로 다 넣어줌 초기값
# visited.append(False)
# print(visited)
def dfs(v):
visited[v] = True # 정점 v 방문
print(v, ' ', end='') # 정점 v 출력
for w in adj_list[v]: # 정점 v에 인접한 각 정점에 대해
if not visited[w]:
dfs(w) # v에 인접한 방문 안된 정점 순환 호출
print('DFS 방문 순서:')
for i in range(n):
if not visited[i]:
dfs(i)- BFS 그래프 순회 연산구현
- 큐를 사용하여 구현
- 반복적 방법을 이용
adj_list = [[2, 1], [3, 0], [3, 0], [9, 8, 2, 1],
[5], [7, 6, 4], [7, 5], [6, 5], [3], [3]]
n = len(adj_list)
visited = [False for _ in range(n + 1)]
def bfs(v):
queue = [] # 리스트로 큐 선언
visited[v] = True
queue.append(v) # 큐에 시작점 삽입
while len(queue) != 0:
u = queue.pop(0) # 큐에서 정점 v를 가져옴
print(u, ' ', end='') # 정점 v 출력(방문)
for w in adj_list[u]: # 정점 v에 인접한 방문 안된 정점에 대해
if not visited[w]:
visited[w] = True
queue.append(w) # v에 인접한 정점을 큐에 삽입
print('BFS 방문 순서:')
for i in range(n):
if not visited[i]:
bfs(i)