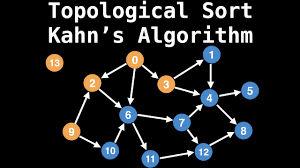
위상 정렬 (Topology Sort)
- 순서가 정해져 있는 작업을 차례로 수행 할 때 사용하는 알고리즘
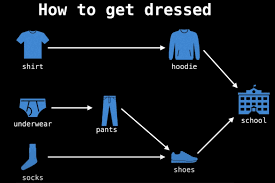
해결 방법
- 진입 차수가 0인 정점(들어오는 간선의 수가 0)을 선택한다.
- 진입 차수가 0인 정점이 여러 개 존재할 경우 어느 정점을 선택해도 무방하나 조건에 따라서.
- 초기에 간선의 수가 0인 모든 정점을 큐에 삽입한다.
- 선택된 정점과 여기에 부속된 모든 간선을 삭제한다.
- 선택된 정점을 큐에서 삭제한다.
- 선택된 정점에 부속된 모든 간선에 대해 간선의 수를 감소시킨다.
- 위의 과정을 반복해서 모든 정점이 선택, 삭제되면 알고리즘 종료한다.
- 파이썬으로 구현
adj_list = [[1], [3, 4], [0, 1],
[6], [5], [3, 7], [7], [8], []]
n = len(adj_list) # 그래프 정점 수
visited = [False for _ in range(n)] # 방문되면 True 로
s = []
def dfs_ts(v):
visited[v] = True # 정점 v 방문
for w in adj_list[v]: # 정점 v에 인접한 각 정점에 대해
if not visited[w]:
dfs_ts(w) # v에 인접한 방문 안된 정점 w에 대해 순환 호출
s.append(v) # v에 인접한 모든 점에 s에 이미 추가되어 있으므로 v를 s에 추가
for i in range(n):
if not visited[i]:
dfs_ts(i)
s.reverse()
print('위상 정렬 순서:', s)
Empire