Gradient Descent(경사 하강법)

유승한·2024년 10월 21일

딥러닝

목록 보기

1/15

1. 정의

경사하강법(Gradient Descent)은 기계 학습과 최적화 문제에서 널리 사용되는 알고리즘으로, 주어진 함수의 최솟값을 찾기 위한 방법입니다. 이 알고리즘은 함수의 기울기(경사)를 이용해 점진적으로 함수의 값을 줄이는 방식으로 작동합니다. 이를 통해 손실 함수 또는 비용 함수의 최소값에 도달하는 것이 목표입니다.

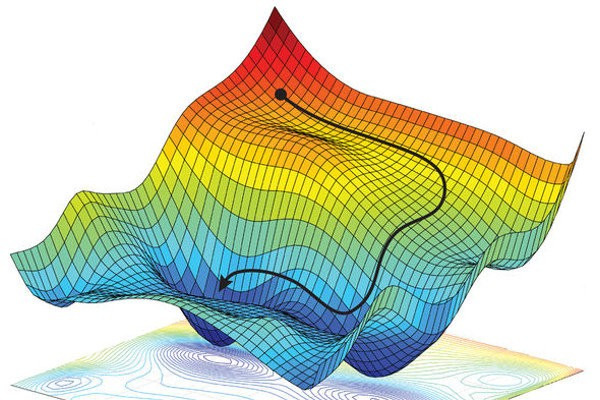
2. 경사 하강법을 사용하는 이유

인공지능은 손실함수를 통해 파라미터를 검증합니다.
- 손실함수는 인공지능의 예측 값과 실제 값의 차이로 최소의 손실 함수 값이 최적의 파라미터라고 할 수 있습니다.
현실의 함수들은 복잡하고 비선형적으로, 미분보다 손실함수를 이용하여 최솟값을 찾는 것이 효율적
- 실제로 미분계수를 계산하는 과정을 컴퓨터로 구현하는 것에 비해 경사 하강법은 컴퓨터로 쉽게 구현 가능합니다.
데이터 양이 매우 큰 인공지능 학습의 경우 특히 경사 하강법과 같은 iterative한 방법을 통해 해를 구하면 계산량 측면에서 더 효율적입니다.

3. 경사하강법을 통해 최솟값을 찾는 방법

기울기 하강법은 기존의 $\theta$ 에서 $\theta+\Delta\theta$ 로 이동했을 시에 기존 로스값인 $L(\theta)$ 보다 작을 때 업데이트 된다. 이를 반복하는데 $L(\theta+\Delta\theta) == L(\theta)$ 가 성립할 대 경사하강법은 멈춥니다. 이를 수식으로 정리하면 위 사진 상단의 수식과 같습니다.

$\theta^* = {argmin\atop{\theta \in \Theta}} L(f_\theta (x), y)$

(argmin은 함수가 최소값을 가지는 입력 값(인수)을 의미합니다.)

이때 $\Delta\theta$ , 즉 이동하는 step의 크기를 어떻게 설정할지에 대한 의문이 생깁니다. step의 크기를 구해주기 위해 테일러 급수를 근사하여 1차 미분값까지만 이용합니다(계산량을 줄이기 위함입니다).

로스함수의 변화량

$L(\theta+ \Delta \theta) - L(\theta) = \Delta L = 기울기L *\Delta \theta$

Step size와 learning rate

$\Delta \theta = -\eta\Delta L, then \Delta L = -\eta ||L 기울기||^2 < 0, where \eta >0$

이때 learning rate를 이용하는 것은 테일러급수의 1차 미분값까지만 이용하기에 아주 좁은 영역에서만 감소방향이 정확하기 때문입니다.(테일러 급수에 대한 설명은 하단의 Appendix 참고하시면 됩니다.) 따라서 learning rate은 매우 작은 수가 됩니다.

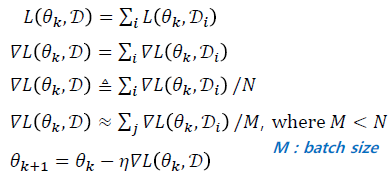
전체 데이터에 대한 손실 함수가 각 데이터 샘플에 대한 손실의 합으로 구성되어 있기에 미분 계산을 효율적으로 할 수 있습니다.

전체 데이터에 대한 손실 미분값의 합을 구한 후 파리미터를 업데이트를 하지만, 실제 학습에서 전체 DB의 미분값(gradient)을 구하기에 연산량이 너무 많기에, 일부 배치에 대해서만 수행합니다. 이때 한번의 업데이트를 step, 모든 training data를 업데이트하는 것을 epoch이라고 합니다.

Deep neural network에서 이러한 경사하강법을 이용하기엔 엄청난 연산량을 요구하는데 이때 Backpropagation Algorithm을 통해 해결하게 됩니다.

p.s. *deep neural network 학습과 maximum likelihood estimation은 상당히 유사합니다.*

4. 경사하강법에서 배치를 이용하는 이유

아래의 3Blue1Brown 동영상을 통해 경사하강법이 어떻게 이루어지는지와 배치를 이용하는 이유를 설명하겠습니다.

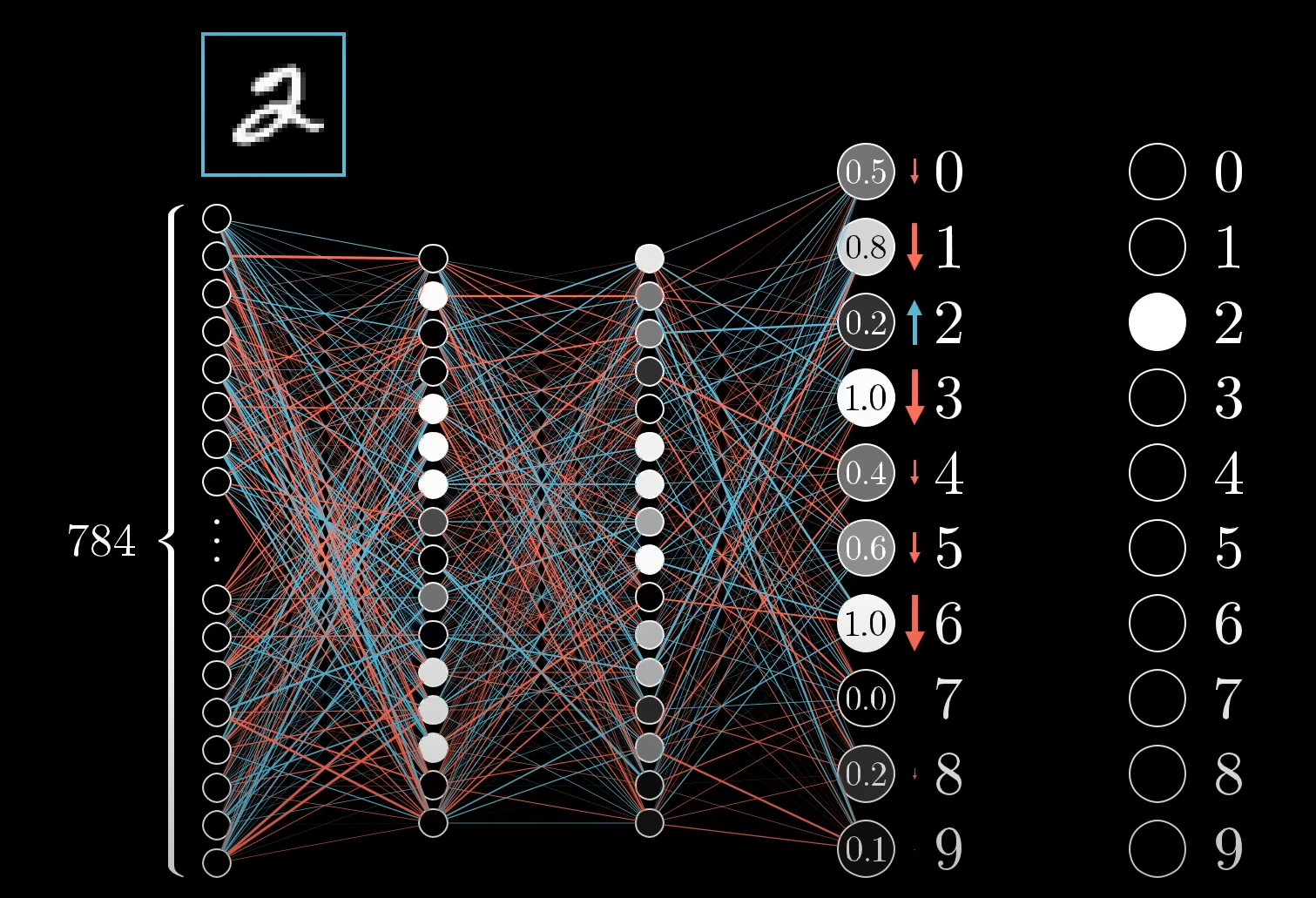
MNIST 데이터 중 2를 판단하는 모델이라고 가정해봅시다. 해당 모델은 학습이 충분히 이루어지지 않아 출력층 뉴런의 값이 정답인 [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]과는 상이합니다. 그렇기에 2에 해당하는 출력층 뉴런은 1에 가깝게 나머지 뉴런은 0으로 가게끔 조정해주는 작업을 진행해야하며, 조정의 크기는 현재 1과 0에 얼마나 가깝고 먼지에 따라 달라질 것 입니다.

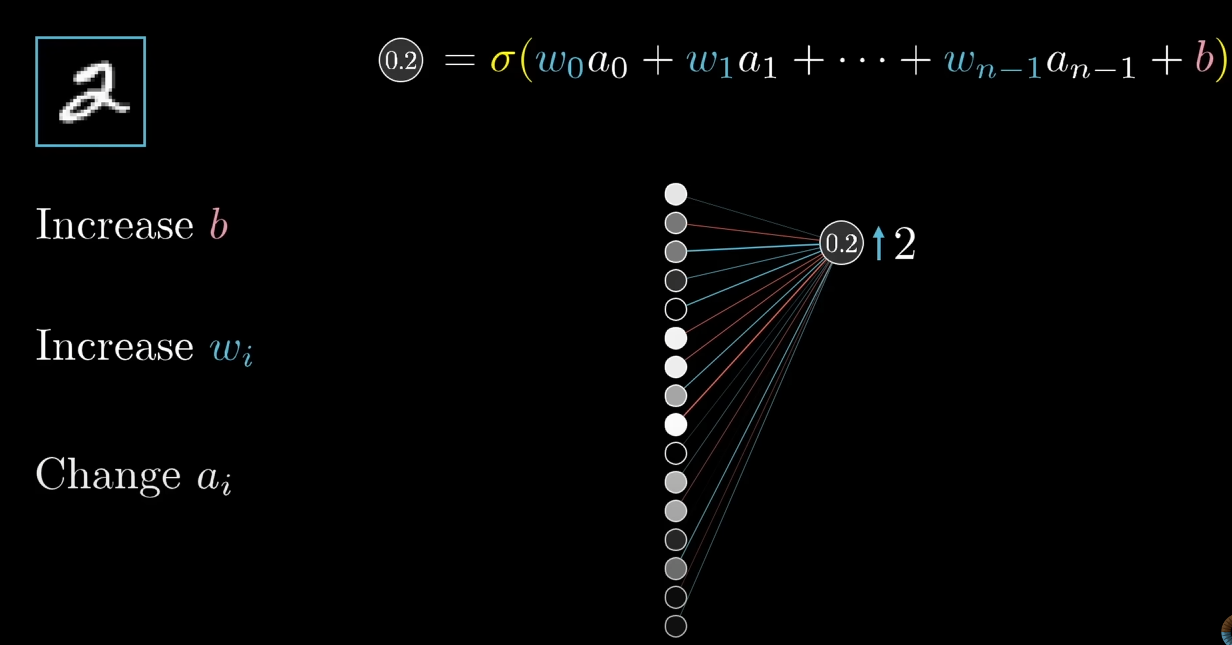
이러한 조정은 $b$ (bias, 편향), $w_i$ (weight, 가중치), $a_i$ (activation, 활성도)에 적용될 수 있습니다. 위 사진과 같이 2에 해당하는 뉴런의 결과값을 높이기 위해서 $b$ , $w_i$ , $a_i$ 를 높임으로서 해결할 수 있습니다.

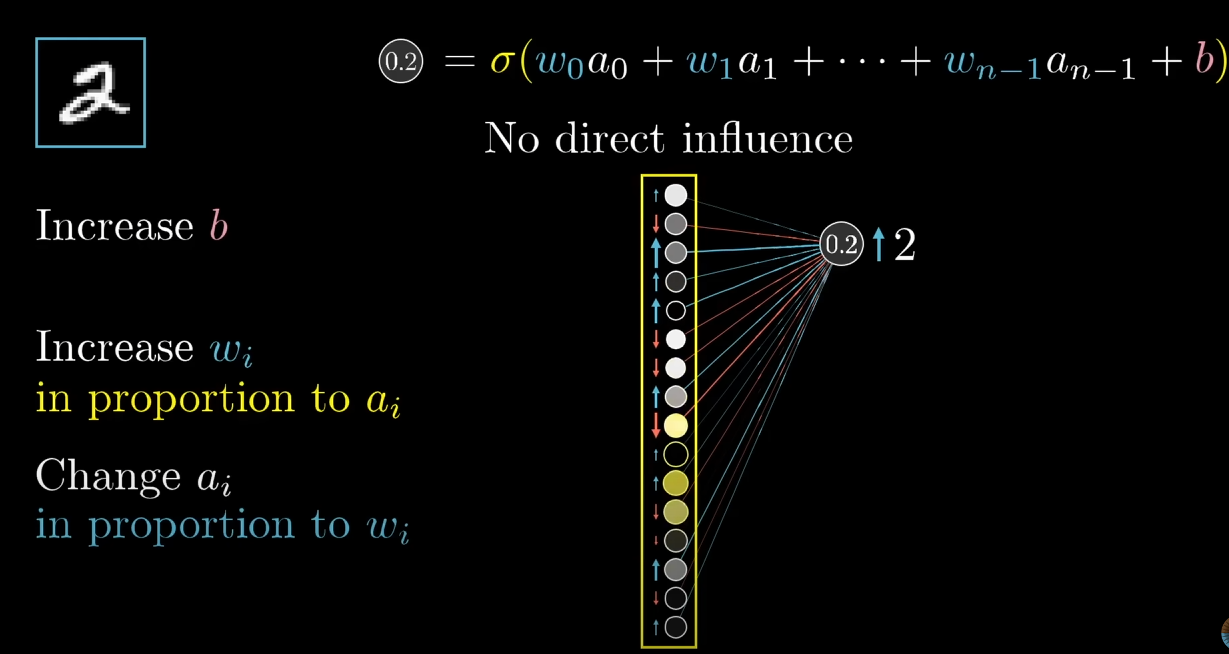
이때 2에 해당하는 뉴런에 강하게 영향을 영향을 주는 $w_i$ 와 $a_i$ 를 조정 시에 이러한 과정은 더 수월하게 이뤄짐을 알 수 있습니다. 하지만 이러한 조정은 직접적인 영향을 준다기보다는 이러한 경향의 변화를 이끌어낼 수 있다 정도로 이해하는게 좋습니다. 수많은 레이어가 있고 모든 레이어를 고려하여 직접적인(구체적인) 영향을 산출해내기 어렵기 때문입니다.

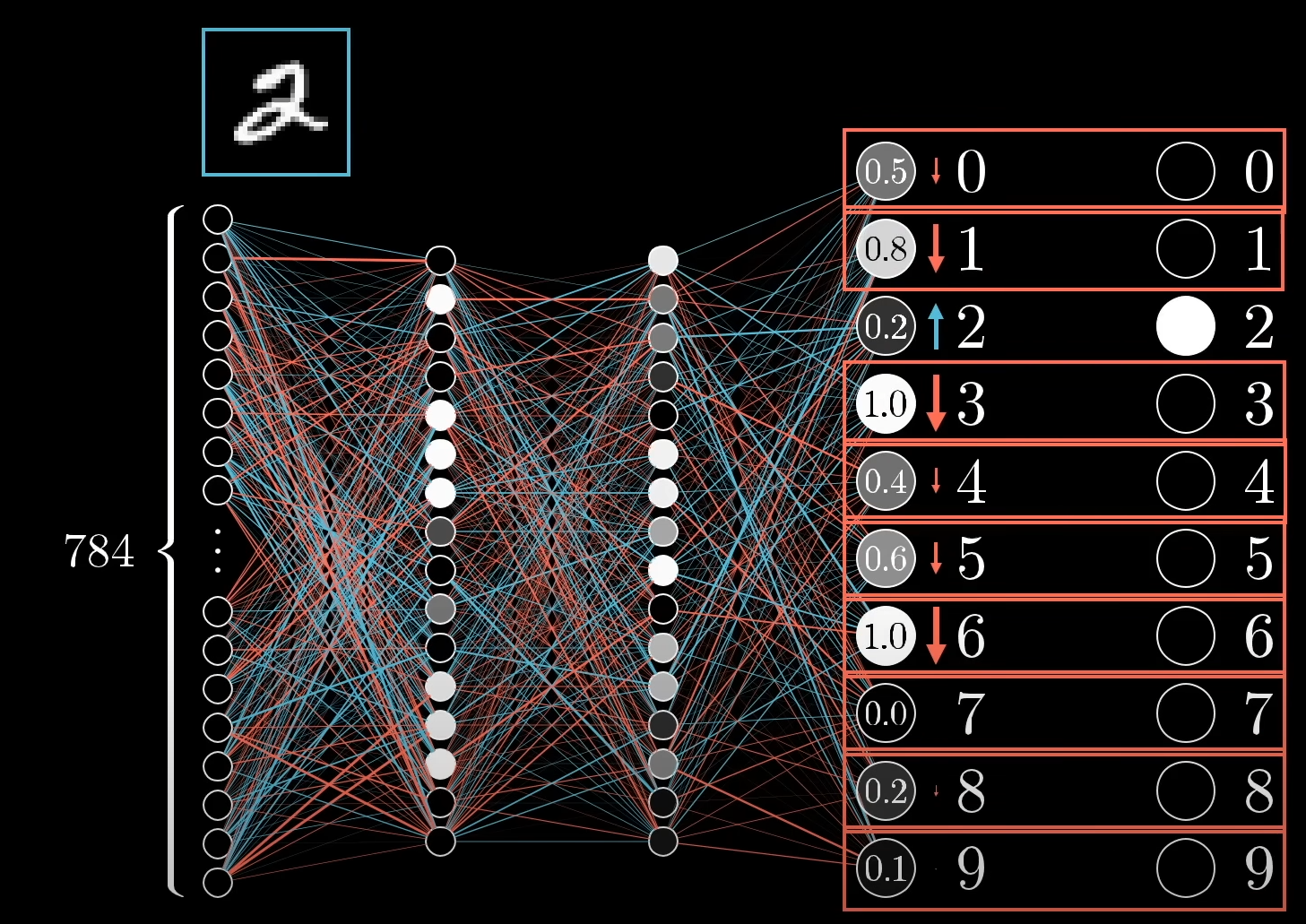
또한 2에 해당하는 뉴런 뿐만이 아닌 전체적으로 모든 뉴런에 대하여 이러한 조정은 이뤄져야 합니다. 따라서 각 층의 $w$ 와 b를 평균 낼 시 비용함수의 음의 기울기와 비례한다고 할 수 있습니다.

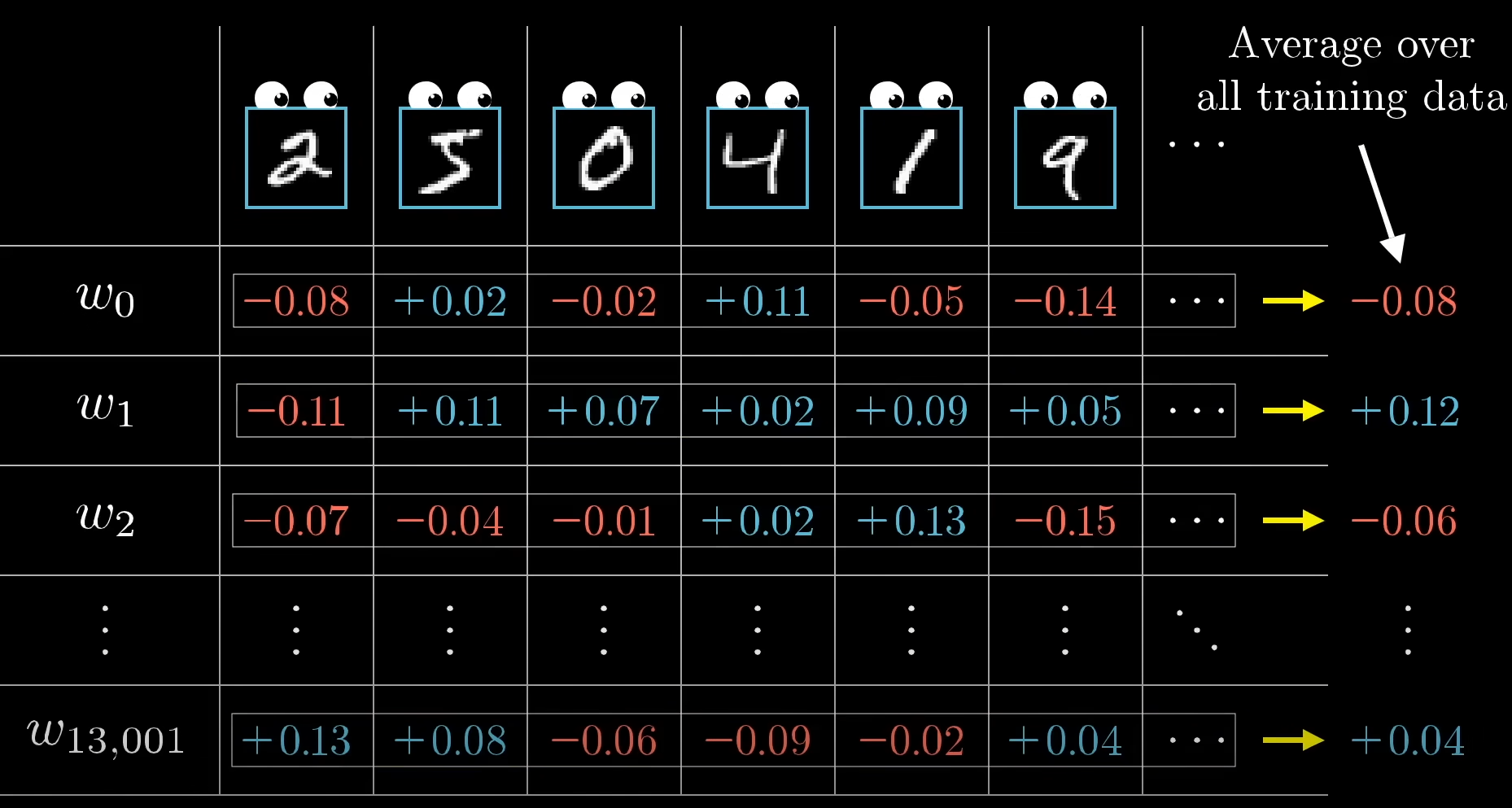
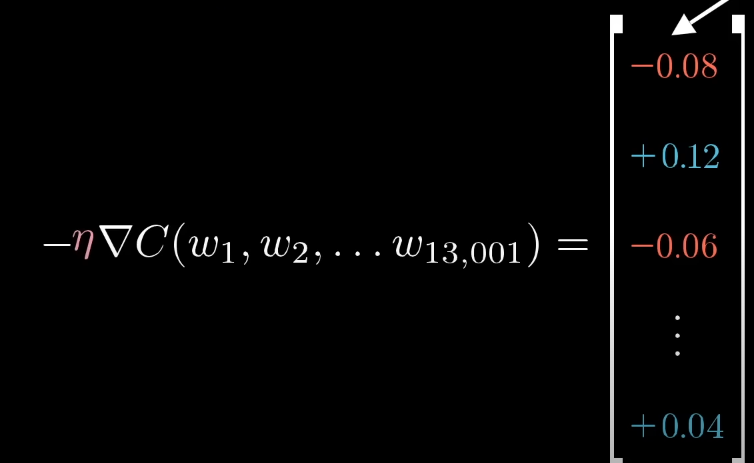
하지만 이러한 연산은 너무 많은 연산량을 요구합니다. 따라서 배치를 이용합니다. 훈련데이터를 배치로 나누어 업데이트함으로써 앞서 계산했던 값의 근삿값을 더 빠른 시간에 구할 수 있게 됩니다. 이를 Stochastic gradient descent(SGD)이라고 합니다.

5. 경사 하강법의 유의점 2가지

적절한 Step size(혹은 learning rate) 설정
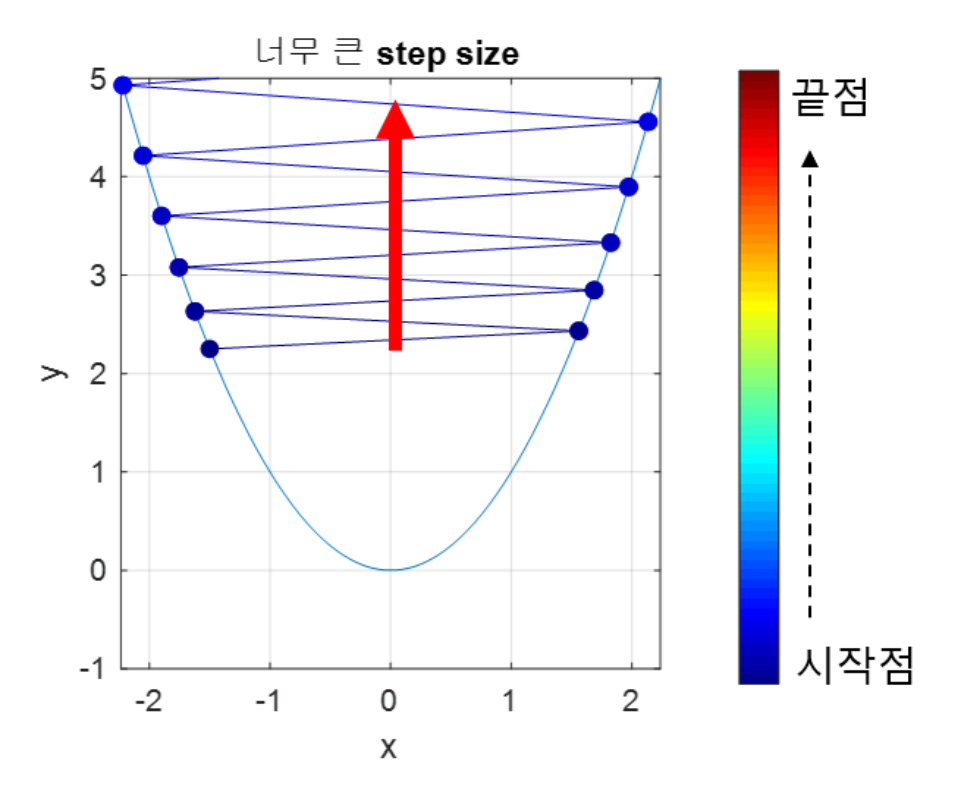
learning rate 설정 시에 너무 크게 설정하여 Step size가 너무 커질 시에 이동하는 크기가 커지므로 빠르게 수렴할 수 있다는 장점이 있지만 손실 함수의 최솟값을 계산하기 어려워지며 함수값이 커지는 방향으로 최적화가 진행될 수 있습니다.

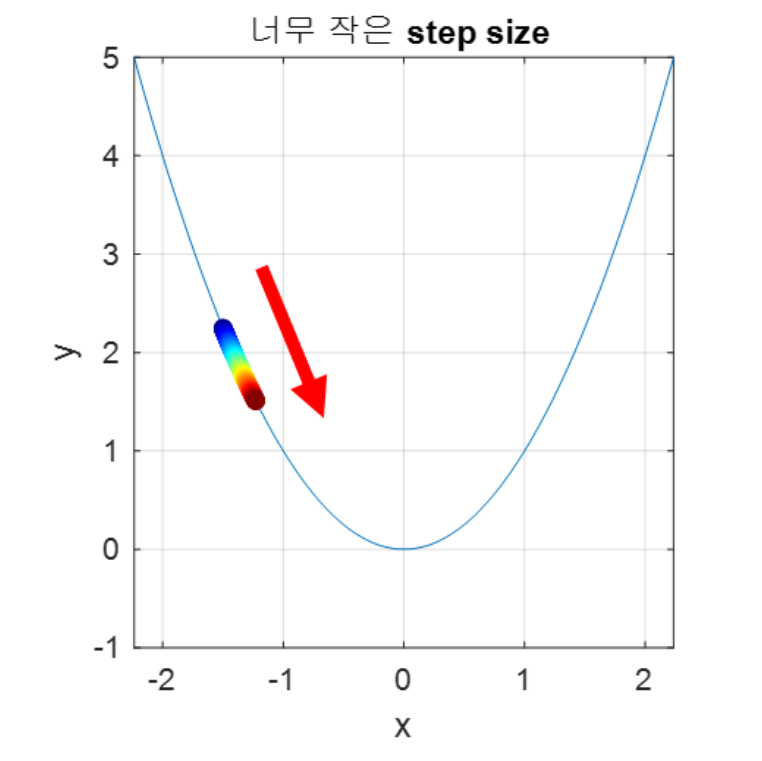
반대로 learning rate 설정 시에 너무 작게 설정하여 Step size가 너무 작을 시에 발산하지 않을 수 있다는 점이 있지만, 최적의 파라미터를 탐색할 때 소요되는 시간이 다소 오래 걸릴 수 있다는 단점이 존재하게 됩니다.

따라서 적절한 learning rate를 조절하는게 중요한데, 사용할 수 있는 방법 중의 하나가 학습 시간 혹은 검증 세트의 손실 값에 따라 학습률을 조절하는 기법을 Scheduling이라고 합니다.
- 이를 해결하기 위해 학습 도중 학습률을 지속적으로 바꾸는 Adaptive Gradient Descent가 존재합니다
Local minima 문제

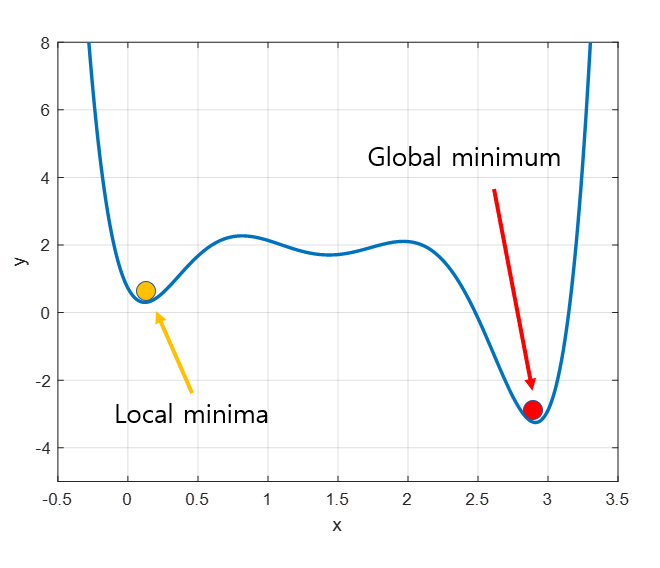
우리는 전역 최솟값을 찾고 싶지만, 지역 최솟값에 빠지는 경우 탈출하지 못하고 해당 위치로 수렴할 가능성이 존재합니다.
- 이를 해결하기 위해 관성력을 추가한 Momentum GD가 존재합니다.