What is Cody?
Cody란 MATLAB의 MathWorks에서 제공하는 프로그래밍 연습 플랫폼입니다. Cody에서는 MATLAB 이용자가 풀 수 있는 다양한 난이도의 문제를 제공하며, 해당 문제의 MATLAB코드를 제출하여 문제 풀이를 이용자들이 학습하고 공유할 수 있습니다.
해당 포스팅은 MATLAB Onramp 강의를 수료 후 학습 차원에서 MathWorks에서 제공하는 여러 Cody문제의 리뷰에 관한 글입니다.
MATLAB을 처음 공부하시는 분들에게 학습한 내용을 적용하며 체화할 수 있는 좋은 학습 도구인 만큼 한 번씩 풀어보면 도움이 될 것 같습니다.
Review
# Problem 44951. Verify Law of Large Numbers
If a large number of fair N-sided dice are rolled, the average of the simulated rolls is likely to be close to the mean of 1,2,...N i.e. the expected value of one die. For example, the expected value of a 6-sided die is 3.5.
Given N, simulate 1e8 N-sided dice rolls by creating a vector of 1e8 uniformly distributed random integers. Return the difference between the mean of this vector and the mean of integers from 1 to N.
# Problem 44951. Solution
function dice_diff = loln(N)
roll = randi(N,1e8,1);
mean_value = mean(roll)
expected_value = mean(1:N);
dice_diff = mean_value - expected_value
end위 문제에서는 먼저 N면을 가지고 있는 주사위로 1~N사이의 난수를 element로 갖는 벡터를 생성해야 합니다. 벡터의 경우 행벡터나 열벡터 모두 상관 없지만 저는 열벡터로 roll 벡터를 생성하였습니다.
roll = randi(N,1e8,1); MATLAB에서 doc으로 도움말 문서를 참고하면 randi함수의 기능을 확인하실 수 있습니다.
X = randi(imax,sz1,...,szN)은 sz1×...×szN 배열을 반환합니다. 여기서 sz1,...,szN은 각 차원의 크기를 나타냅니다. 예를 들어, randi(10,3,4)는 1과 10 사이의 정수형 의사 난수로 구성된 3×4 배열을 반환합니다.
저는 1~N사이의 난수인 정수값을 요소로 갖는 1e8 1 크기의 열벡터를 생성하였습니다.
(1e8은 매트랩에서 지수를 표현하는 방식으로 e는 10의 거듭제곱을 표현하여 1 10^8임을 나타냅니다. 비슷한 방식으로 3.14e5는 3.14 * 10^5값을 나타냅니다.)
mean_value = mean(roll)
expected_value = mean(1:N); 이후 mean함수를 이용하여 벡터 혹은 행렬의 평균값을 계산합니다.
첫 번째 코드는 주사위를 굴려 랜덤하게 생성한 열벡터에 대하여 모든 요소의 평균값을 반환하여 mean_value변수에 저장하고, 두 번째 코드는 1:N을 통해 생성한 [1 2 3 ... N] 행벡터를 생서한 뒤, 이에 대한 기댓값(expected value)를 계산합니다.
dice_diff = mean_value - expected_value 마지막으로 시뮬레이션하여 구한 평균값과 기댓값의 차이를 반환합니다.
# Problem 44946. Solve a System of Linear Equations
Given a constant input angle θ (theta) in radians, create the coefficient matrix (A) and constant vector (b) to solve the given system of linear equations in x₁ and x₂.
cos(θ) x₁ + sin(θ) x₂ = 1
-sin(θ) x₁ + cos(θ) x₂ = 1
위 문제를 통해서는 매트랩에서 선형 연립방정식을 해결하는 mldivide 함수의 이용법을 익힐 수 있었습니다. mldivide 함수의 도움말 문서를 참고하면,

x = mldivide(A,B)는 선형 연립방정식 A*x = B의 해를 구합니다. 행렬 A와 B의 행 개수는 동일해야 합니다.
위 설명에서 A는 선형 연립방정식의 Coefficient matrix, B는 unknown vector에 해당합니다.
# Problem 44946. Solution
function x = solve_lin(theta)
A = [ cos(theta) sin(theta); -sin(theta) cos(theta)]
b = [1;1]
x = A\b;
end# Problem 44948. Calculate a Damped Sinusoid
The equation of a damped sinusoid can be written as
y = Ae^(-λt)cos(2πft)
where A, λ, and f are scalars and t is a vector.
Calculate the output sinusoid y given the inputs below:
lambda - λ
T - maximum value of t
N - number of elements in t
Assume A = 1 and f = 1 . The vector t should be linearly spaced from 0 to T, with N elements.
위 문제를 통해서는 방정식에서 input값이 행벡터 혹은 열벡터로 들어가는 경우에 코드를 어떻게 표현해야 하는가에 대해 체득할 수 있었습니다.
# Problem 44948. Solution
function y = damped_cos(lambda, T, N)
t = linspace(0,T,N)
y = exp(-lambda * t) .* cos(2*pi*t)
end t = linspace(0,T,N)우선 damped sinusoid equation에서 벡터 t의 값이 0에서 T사이의 값이 N개의 elements로 할당되어야 하므로, 벡터를 만들어주는 함수 중 element의 구간과 element수를 지정하여 만들 수 있는 linspace함수를 활용하여 벡터 t를 만들어 주었습니다.
y = exp(-lambda * t) .* cos(2*pi*t)이 후 주어진 damped sinusoid equation을 작성해주면 문제를 해결할 수 있습니다.
유의할 점은 input으로 벡터값을 넣어주기 때문에 연산 시에도 벡터 각각의 요소에 대한 연산이 필요하기 때문에 곱셈을 사용시에 ""가 아닌 "."를 활용해주어야 합니다.*
# Problem 44934. Plot Damped Sinusoid
Given two vectors t and y, make a plot containing a blue ( b ) dashed ( -- ) line of y versus t.
Mark the minimum value m of the vector y by adding a point to the plot. This point should be a red asterisk marker, and it must be added after the blue line.
Return the minimum value of y as output m.
위 문제를 통해서는 plot함수의 여러 사용방법을 익히고 적용할 수 있었습니다.
우선 문제에서 요구하는 바와 같이 플롯에 여러 그래프의 요소를 같이 플로팅하기 위해서는
hold on을 활용하여 같은 플롯에 플로팅할 것을 활성화 합니다.
이후 t벡터에 대한 y벡터 값을 blue dashed line으로 표시되도록 plot함수로 플로팅합니다.
plot(t,y,"b--")이제 그래프의 플로팅은 모두 끝났습니다. 다음으로 y벡터에서 최솟값과 최솟값의 인덱스를 구하여 변수 min_y, idx_min_y에 저장합니다.
[min_y, idx_min_y] = min(y)마지막으로 그래프의 y의 최솟값 지점에 red asterisk marker를 표시할 차례입니다. 표시에 앞서 먼저 plot함수를 활용하여 점을 플로팅하는 방법에 대해서 생각해봅시다.
plot(x,y) 함수의 경우에는 기본적으로 x에 대한 y값을 플로팅합니다. 이 때 x와 y는 벡터에 해당할 것입니다.
Q. 그렇다면 하나의 점의 표현은 어떻게 할 수 있을까?
하나의 점은 벡터의 size가 1인 경우로 생각하면 되므로 plot(a,b)에서 a와 b에 각각 점을 찍고 싶은 특정 값을 숫자로 넣어주면 해당 지점에 점을 찍을 수 있게 됩니다.
plot(3,2,"bx")위의 예시의 결과로는 이전의 플롯에 (3,2)에 해당하는 지점에 파란색 x모양의 점을 표기할 수 있을 것입니다.
그렇다면 돌아와서 Plot Damped Sinusoid 문제를 다시 해결해봅시다. y값이 최소인 지점에 빨간색 *모양의 점을 표기해야하므로 다음과 같이 코드를 작성하면 됩니다.
plot(t(idx_min_y), min_y, "r*")먼저 t축에 대해서는 앞서 구한 y의 최솟값에 해당하는 인덱스값을 이용하여 이에 대응되는 t축의 인덱스 값을 점을 찍을 t축 값을 a위치에 입력해줍니다. 그리고 y축 값의 경우 min_y값으로 설정합니다. 이와 같이 입력하면 y의 최솟값에 해당하는 t축과 y축값의 인덱스 입력이 완료됩니다. 이 후 점의 색과 모양을 설정하여 표기합니다.
마지막으로 함수의 output값은 m에 min_y값을 반환하도록 합니다.
m = min_y함수 실행 결과 플로팅된 모습은 다음과 같습니다.
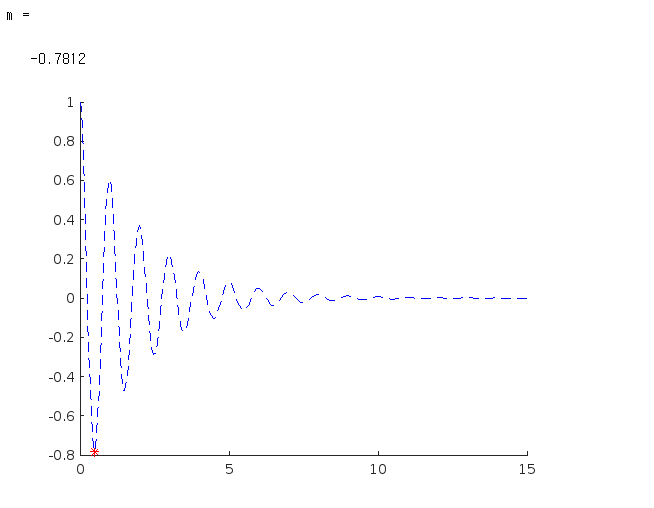
# Problem 44934. Solution
function m = plot_cos(y, t)
hold on
plot(t,y,"b--")
[min_y, idx_min_y] = min(y)
plot(t(idx_min_y), min_y, "r*")
m = min_y
hold off
end