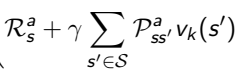"앞으로 강화학습에 다루게 될 포스팅은 Google DeepMind에서 제공하는 RL Cource by David Silver 강의를 듣고 강의자료를 참고하여 개인적으로 리뷰하는 내용입니다. 개인적인 학습 및 리뷰가 주된 목적이므로 강의의 모든 내용을 포함하지 않을 수 있으며 핵심적이거나 제가 이해하기 어려웠던 내용들을 다룰 것임을 포스팅에 앞서 알립니다."

Introduction to Planning by DP

2장에서는 강화학습(Reinforcement Learning)을 적용하기 적합한 문제인 순차적 문제 해결(Sequential Decision Making)과 그 문제해결을 위한 Markov Decision Process(MDP)에 대해 공부하였습니다.

2장에서 학습한 MDP를 적용한 다양한 문제는 full knowledge의 여부-"모델의 모든 정보를 알고 있는가?"에 대한 특성-에 따라서 Model-based method(Planning)와 Model-free method(Learning)로 나뉩니다. 3장에서는 MDP를 적용한 다양한 문제에서 full knowledge-State transition probabilty와 policy값을 포함하여 모든 정보를 알고 있는-인 Model-based method인 Planning 문제 해결방법에 대하여 공부합니다.

우리가 강화학습을 적용하여 해결하고자 하는 대부분의 문제는 문제의 규칙이나 문제상황에 대해서 모르는 경우인 Model-free인 경우가 많기 때문에 Learning 문제 해결방법이 더 실용적입니다.

하지만 Planning 문제해결방법을 응용하여 본격적인 강화학습 모델 Reinforcement Learning인 Monte-Carlo Learning(MC), Temporal-Difference Learning(TD)로 발전되기 때문에 Planning method에 대한 이론을 정확하게 공부할 필요가 있습니다.

---

What is Dynamic Programming?

Dynamic Programming이란 여러 알고리즘에 적용되는 패러다임으로 복잡한 하나의 문제를 여러 개의 작은 문제들로 나누어 재귀적으로 해결할 때 사용하는 알고리즘 기법입니다.

해결한 작은 문제의 결과를 활용하여 재귀적으로 다음 문제를 해결하다보면 최종적으로 아주 복잡한 문제를 간단히 해결할 수 있습니다.

지난 학기 알고리즘 및 문제해결기법 강의를 들었었는데, 수업 때 공부한 DP문제를 예시로 들자면 Assembly-line scheduling(Graphical Algorithm), Rod cutting, Matrix-chain multiplication 등이 있습니다. 또한 다양한 Graph Algorithm의 문제해결에도 활용될 수 있습니다.

(본 포스팅에서는 Planning 문제 해결을 위한 (Synchronous)Dynamic Programming algorithm에 관해 다룰 예정입니다.)

Requirements for Dynamic Programming

Dynamic Programming을 적용하기 위해서는 다음과 같은 두 가지 특성을 만족해야 합니다.

Req1. Optimal Structure

해결하고자 하는 문제는 Principle of Optimality를 만족하는 여러 개의 작은 문제로 나뉘어질 수 있습니다.

" 해결한 작은 문제의 최적 결과값은 목표했던 전체 문제의 해결을 위해 활용될 수 있습니다. "

Req2. Overlapping subproblems

Optimal Structure로 나눈 문제들은 재귀적인 구조를 가져야 합니다. 따라서 나누어진 작은 문제는 목표했던 전체 문제 해결하는 과정에 있어서 동일한 작은 문제로 중복하여 나타납니다.

Markov Decision Process로 정의한 문제는 두 특성을 모두 만족한다는 점에서

1. MDP의 Bellman Equation은 재귀적으로 문제가 나뉘어져 Overlapping subproblems를 만족
2. 부분적인 문제의 결과값은 전체 문제 해결을 위해 사용되어 Optimal Structure 만족-

Dynamic Programming으로 해결하기에 적합한 문제라 할 수 있습니다.

Classification of Planning

1. Policy Iteration

2. Value Iteration

Planning 문제의 해결방법은

"문제해결을 위하여 explicit policy 개념을 도입하는가?"

의 여부에 따라서 Policy Iteration과 Value Iteration으로 분류할 수 있습니다.

(policy의 개념은 MDP 문제정의에서 다뤘던 내용으로 Lecture #2 포스팅 글에서 관련 내용을 확인하실 수 있습니다.)

---

Policy Iteration

Policy Iteration은 policy 개념을 도입한 문제해결 알고리즘으로서
현재 적용한 policy를 평가하는 문제인 Policy Evaluation과 policy evaluation을 통한 평가를 바탕으로 greedy policy improvement를 통하여 optimal policy를 결정하는 Policy Improvement로 구분할 수 있습니다.

1 . Policy Evaluation

첫째로 현재 policy 평가를 위한 Policy Evaluation입니다.

Policy Evaluation의 목표는 given policy π를 평가하는 것입니다.

주어진 현재 policy를 평가하기 위해서는 MDP에서 정의에 활용했던 Bellman expectation equation을 iterative한 방법으로 업데이트하며 수렴할 때까지 반복적으로 계산합니다.

Bellman expectation equation 해결을 위한 Policy Evaluation식과 표현한 그래프는 아래와 같습니다.

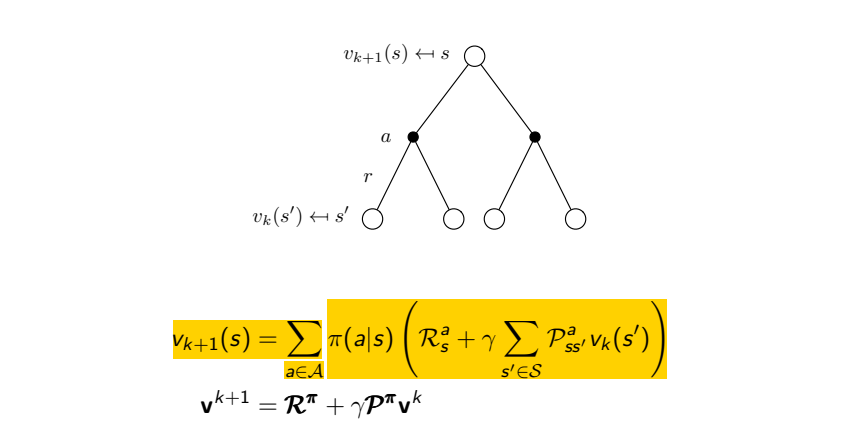
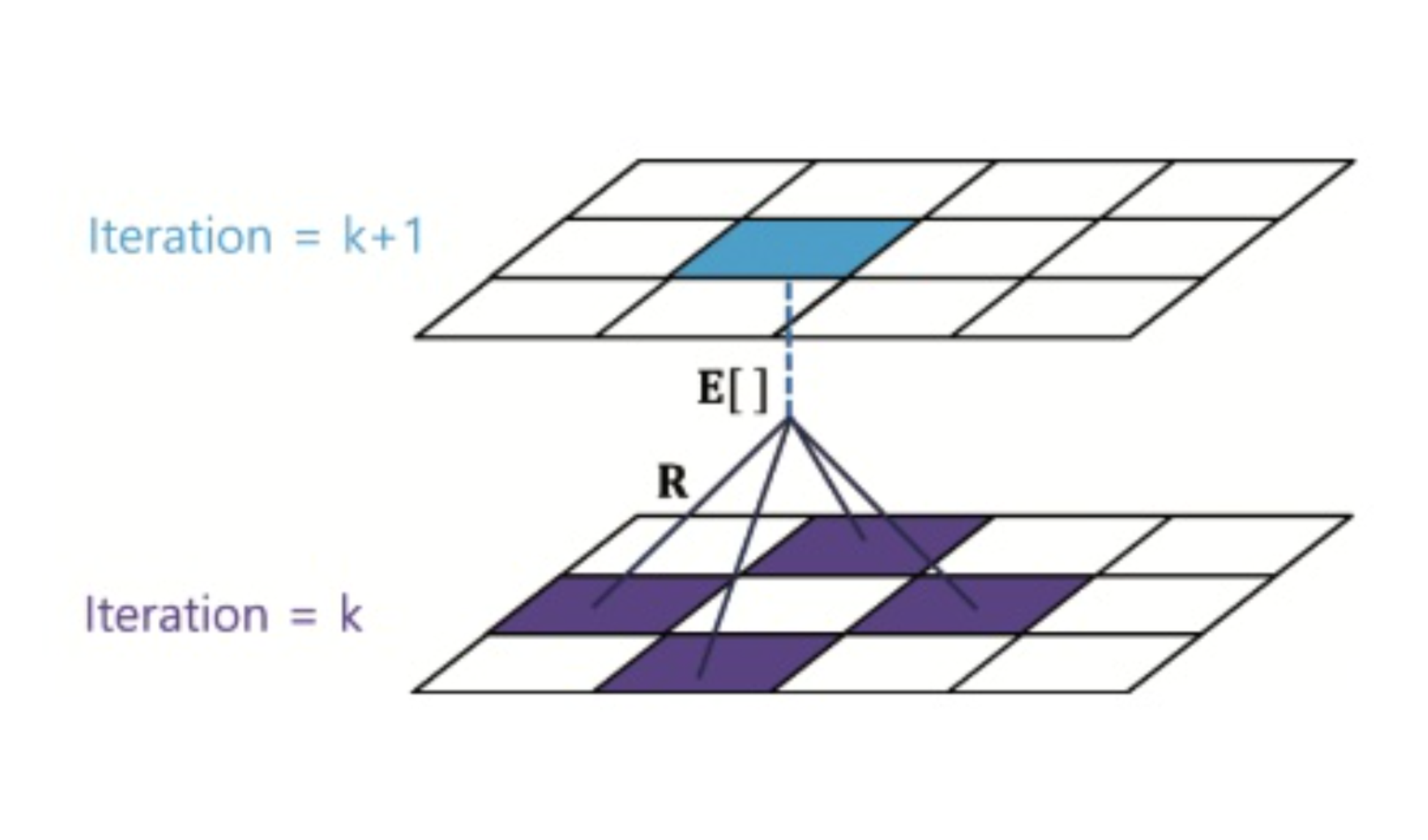
Policy Evaluation에서는 문제에서 정의한 모든 state에 대하여 현재 state s에서 행동할 수 있는 모든 action에 대한 상황을 모두 고려하여 value function을 업데이트합니다.

EX) 이해를 돕기 위하여, 이를 상하좌우로 움직이는 Grid Wolrd 문제상황에 대하여 Policy Evaluation에 대해 그림으로 표현해보면 아래와 같습니다.


현재(t=k) 시간에 대하여 하나의 step이 지난 미래(t=k+1)의 value function값은 상하좌우의 action에 대한 Bellman expectation equation값을 해결한 기댓값으로 계산됩니다. 이러한 계산을 모든 state에 대해 적용하여 각각의 state에 대한 value function값을 업데이트합니다.

그림 3.1. Bellman expectation equation을 이용한 현재 상태의 value function 업데이트

Planning 문제에서는 MDP environment에 관한 모든 정보
(식에서 P로 표현된 State transition probability & action에 따른 policy π)를
알고 있으므로 위 식을 활용하여 Bellman expectation equation을 해결할 수 있습니다.

How to Improve a Policy?

Policy Improvement에 대해 본격적으로 설명하기 전에 Policy Iteration의 순서에 대해서 간단히 소개하고 넘어가보려 합니다.

Policy Evaluation에서 true value function값을 얻기 위해서는 value function이 수렴할 때까지 반복적으로 값을 계산해야 합니다.


하지만 수학적인 증명에 따르면(이 부분은 포스팅에서 생략할 예정입니다.)
하나의 step에 대하여 Evaluation과 Improvement를 한 번씩 진행하여 value function과 optimal policy를 업데이트하더라도 policy iteration이 최종적으로는 동일하게 Optimal policy에 수렴하게 되므로,
위와 같이 Policy Iteration과정은 한 step에 대하여 Evaluation과 Improvement를 1번씩 수행하여 Optimal policy가 수렴할 때까지 iteration을 진행합니다.

2 . Policy Improvement

두 번째로 Policy Evaluation에서 평가한 policy의 평가값을 바탕으로 Optimal policy를 결정하는 Policy Improvement입니다.

Policy Improvement는 policy evaluation과정에서 계산한
q-function값에 대하여 Greedy policy Improvement를 적용하여 최적의 정책 Optimal policy를 업데이트합니다.

Policy iteration의 전체적인 흐름을 나타낸 다이어그램은 아래와 같습니다.

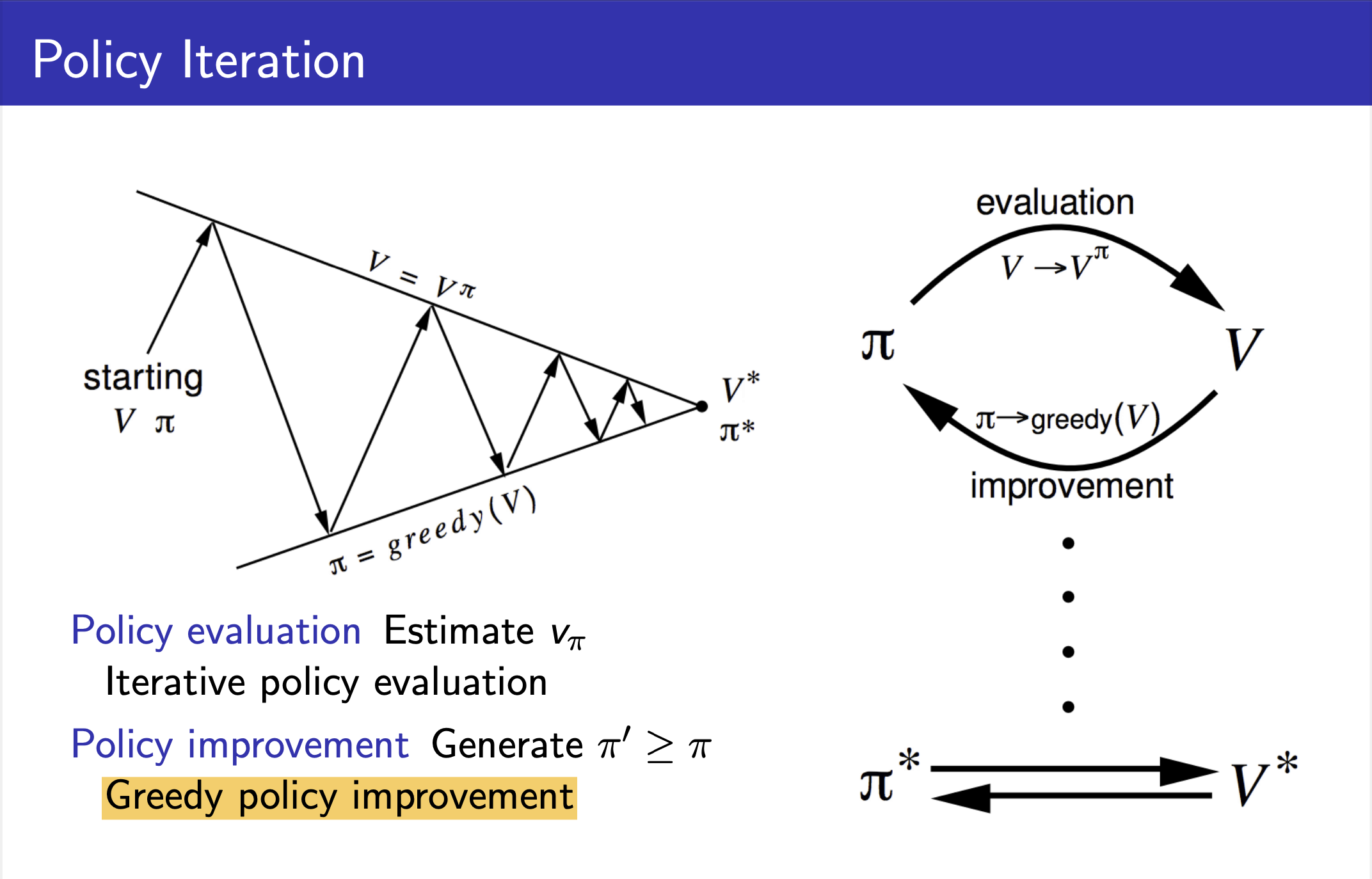
왼쪽 첫번째 그림과 같이 한 번의 Policy evaluation과 Policy improvement를 반복하다보면 최종적으로 구하고자 하는 true value function값에 다다를 수 있습니다. (David Sliver 강의에서는 이에 대한 수학적 증명 역시 생략합니다.)
또한 true value fucntion값을 토대로 Planning 문제의 궁극적인 목표인 Optimal policy 역시 도출할 수 있습니다.


Q. 그렇다면 Policy evaluation을 토대로 Policy Improvement는 어떻게 할 수 있을까요?

A. Policy improvement 정책 발전에는 다양한 방법들이 존재하지만 David Silver강의를 포함한 대부분의 기본서에서는 대표적인 정책발전 예시로 Greedy Policy Improvement를 들고 있습니다.

Greedy Policy Improvement

탐욕 정책 발전 Greedy Policy Improvement 과정은 단순합니다.

말 그대로 Greedy하게 현재 state에서 미래에 가장 큰 이익을 줄 것으로 예상되는 가장 큰 q-function(action-value function)값을 갖는 action을 수행합니다. 이를 식으로 나타내면 다음과 같습니다.

EX) 아래 그림은 greedy policy improvement를 이해하기 쉽도록 Grid World 환경에서 나타낸 그림입니다.
그림 3.2. Agent는 Greedy policy improvement를 적용하여 현재 state에서 q-function값이 가장 높은 action을 선택한다.


현재 회색 state에 위치하고 있는 Agent는 현재 state에서 취할 수 있는 상하좌우의 action에 대하여 q-function값을 각각 비교합니다. (여기서 q-function값은 검은색 화살표로 표시되어 있습니다.) 그 중 가장 큰 q-function값을 갖는 action을 한 step에 대한 optimal policy로 선택합니다. 위 그림에서는 현재 state에 대해 q-function값이 가장 큰 보라색 state를 향한 action을 선택합니다.

greedy policy improvement는 각 step에 대해서 수렴할 때까지 iterative하게 이루어지는데, greedy policy improvement를 적용하면 현재 시간 t에서의 value function값보다 한 step이 지난 다음 시간 (t+1)에서의 value function값이 높게 되므로 step을 거칠 때마다 얻는 reward가 점점 커지게 됩니다.




>>> 결론적으로 Policy Evaluation과 Policy Improvement를 반복하여 step 시간에 따른 Optimal policy를 업데이트하면 " 최종적으로 각각의 state에 대하여 수렴하는 Optimal Policy값을 도출" 할 수 있습니다.

* 관련 내용의 증명에 관한 내용은 아래 강의자료 내용을 참고하시길 바랍니다.

---

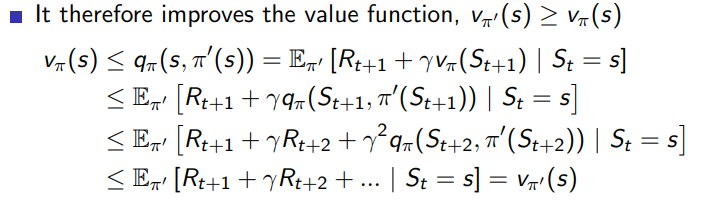
Value Iteration

Value Iteration은 Policy Iteration과 달리 explicit policy개념을 활용하지 않기 때문에 value function값을 통하여 evaluation과 control 과정을 구분하지 않고 자연스럽게 한 번에 진행하는 Planning 문제 해결방법입니다.

Value Iteration에서는 value function 안에 Optimal policy에 대한 개념이 내재적 implicit 으로 포함되어 있으므로 value function을 수렴하도록 업데이트하면 자연스럽게 해결하고자 하는 문제의 최종적인 Optimal policy를 도출할 수 있습니다.

MDP에서 Policy Iteration은 Bellman expectation equation을 해결하는 반면에, Value Iteration에서는 Bellman Optimality equation을 해결하여 최종적으로 Optimal policy를 얻는 것이 목적입니다.

Bellman Optimality equation 해결을 위한 Value Iteration 식과 표현한 그래프는 아래와 같습니다.

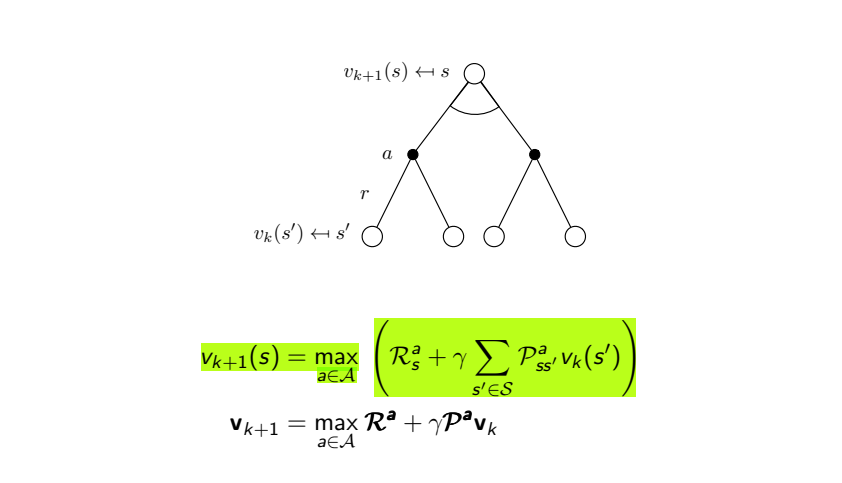
Policy Iteration은 policy π 값을 괄호로 표현된 값에 곱한 후 모든 action에 대해 값을 더하여 value function의 기댓값을 계산했다면,

Value Iteration은 먼저 최상단의 현재 state에서 취할 수 있는 모든 action에 대한 다음 state에서의 reward와 value function 값을 고려해 계산한 값을 각각 구한 뒤, max함수를 통하여 가장 큰 값으로 value function을 업데이트합니다.

EX) 아래 그림은 Value Iteration을 이해하기 쉽도록 Grid World 환경에서 나타낸 그림입니다.
그림 3.3. 현재 state에 대하여 계산한 각각의 괄호값에 대해 max값으로 미래의 value function값을 업데이트한다.


Value Iteration에서는 현재(t=k) state(보라색 왼쪽)에 대하여 취할 수 있는 모든 action(상하좌우)에 대하여 계산한
값이 가장 큰 action만을 선택하여 미래(t=k+1)의 value function 값을 업데이트합니다.


위 그림에서는 현재 state에 대해 오른쪽으로 action한 보라색 state에서의 value function 값이 가장 크므로 해당값으로 미래의 value function값을 업데이트합니다.

>>> 결론적으로 Value Iteration을 통해 해당 step에 대해 value function값이 높은 action을 선택하며 value function을 업데이트 해나가면 "그 값은 true value function값에 수렴"하게 됩니다. 또한 "수렴한 value function값을 통하여 현재 state에 대한 Optimal Policy를 구할 수 있습니다."

---

Sychronous Dynamic Programming for Planning

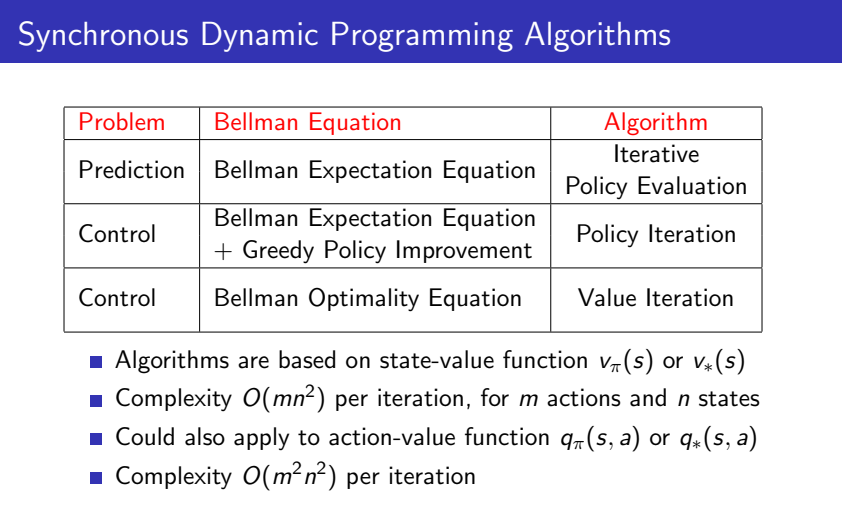
MDP의 구분한 problem 유형과 해결한 equation을 기준으로 어떤 알고리즘이 사용되는지 구분해보면서 이번 포스팅에서 소개드린 알고리즘을 정리하고자 합니다.

1. 먼저 표에서 1,2행의 prediction과 control 관련 내용이 "Policy Iteration"에 해당합니다.
   Policy Iteration에서는 MDP를 Prediction과 Control로 구분하여 policy를 평가하고 optimal policy를 결정하는 과정이 나뉘어져 있습니다. 알고리즘에서 policy를 고려하여 기댓값을 계산하기 때문에, Bellman expectation equation을 해결하고, control 과정에서는 greedy policy improvement를 적용하여 기댓값이 가장 큰 action을 선택합니다.

2. 표의 3행은 "Value Iteration"에 해당합니다. Value Iteration에서는 explicit policy개념이 존재하지 않아 Bellman optimality equation을 해결하는 과정에서 내재적으로 optimal policy를 도출해낼 수 있습니다.
   
   

Limitation of Dynamic Programming

마지막으로 MDP의 Planning 문제 해결을 위한 Dynamic Programming(Policy Iteration & Value Iteration)의 한계점에 관한 내용을 다루며 포스팅을 마무리하고자 합니다.

DP의 한계점으로는 크게 3가지를 꼽을 수 있습니다.

Full-Width Backups

Dynamic Programming은 현재 state에 대하여 가능한 모든 succesor state에서의 value function값을 활용하여 현재 value function값을 업데이트하는 Full-Width Backups를 사용하고 있습니다.

따라서 모든 succesor state에 대해 계산을 수행하게 되는데, 이에 따른 DP의 한계는 다음과 같습니다.

1. High Time Complexity

DP는 m개의 action과 n개의 state에 대하여 총 O(mn^2)의 시간복잡도를 가집니다. 이는 해결한 문제의 environment가 복잡하다면 계산량이 아주 방대하다는 한계가 있습니다.

EX) DP를 활용하면 바둑 - 바둑에서는 MDP를 위해 필요한 state수가 이론적으로 3^19*19 (≈10^172)에 달합니다. 이는 현대 과학기술로 관측할 수 있는 우주의 수소원자 수보다 많은 것으로 알려져 있습니다.- 과 같은 문제의 계산량을 감당하기에 한계가 있습니다.

2. Curse of Dimensionality

비슷한 한계점으로 Curse of Dimensionality를 들 수 있습니다. MDP 문제 정의 과정에서 state의 차원 Dimensionality이 늘어난다면 state의 수가 지수적으로 증가한다는 한계가 있습니다. 증가한 state의 수에 따라 Time Complexity는 더 지대하게 늘어날 것입니다.

3. Necessity for full knowledge in environment

Dynamic Programming은 environment에 대한 모든 정보를 알고 있는 Planning 문제 해결을 위하여 사용되는 알고리즘입니다.

실제로 해결하고자하는 복잡한 문제들은 environment에 대해 알지 못하는 - 앞서 말씀드렸던 Model-free - 경우가 많기 때문에 DP는 복잡한 문제 해결을 위한 접근 자체에 어려움이 있을 수 있습니다.

>>> 이러한 Dynamic Programming의 한계점을 해결하고자 발전된 알고리즘이 Model-free-method에 해당하는 " Reinforcement Learning " 입니다.

본격적으로 다음 강의 내용 review 포스팅에서는 이러한 한계점을 해결한 Reinforcement Learning으로 Monte-Carlo Algorithm과 Temporal Diffrence Algorithm을 다룰 예정입니다.

---

* Reference
Lecture3 강의자료 : https://www.davidsilver.uk/teaching/
Policy Evaluation/Improvement & Value Iteration image : 이웅원, 양혁렬, 김건우, 이영무, 이의령 지음, 『파이썬과 케라스로 배우는 강화학습』, 위키북스 p.72, 75, 95