"앞으로 강화학습에 다루게 될 포스팅은 Google DeepMind에서 제공하는 RL Cource by David Silver 강의를 듣고 강의자료를 참고하여 개인적으로 리뷰하는 내용입니다. 개인적인 학습 및 리뷰가 주된 목적이므로 강의의 모든 내용을 포함하지 않을 수 있으며 핵심적이거나 제가 이해하기 어려웠던 내용들을 다룰 것임을 포스팅에 앞서 알립니다."
Introduction to Model-Free Prediction
3장에서는 Model-based method(Planning) 문제-"모델의 environment에 대한 모든 정보를 알고 있는 모델(known MDP)-의 해결방법인 Policy Iteration과 Value Iteration에 대해서 공부하였습니다.
하지만 Planning 문제의 유형은 우리가 강화학습을 적용하여 해결하고자 하는 문제와 본질적인 차이가 있습니다.
우리는 단순히 모델의 환경을 알고 있는 간단한 문제-Model-based method-를 해결하기 위해 강화학습을 이용하는 것이 아닙니다. 우리는 강화학습을 적용하여 environment에 대한 정보가 하나도 없는, 해결하기 힘든 매우 복잡한 환경에서의 문제를 해결하는데 관심이 있습니다.
4장부터는 본격적으로 우리가 강화학습을 적용하여 해결하고자하는 문제. 즉, "모델의 environment에 대한 정보를 알고 있지 않은" Model-free method(Learning) 문제의 해결방법에 대하여 소개합니다.
모델에 대한 정보가 없는 Learning 문제의 해결은 크게 아래의 두 단계로 구분할 수 있습니다.
Learning Steps of unknown MDP
Step1. Model-free prediction
Estimate the value function of an unknown MDP
첫 번째로는 agent가 정보가 없는 환경에 대해 상호작용하며 설정한 policy에 대한 value function값을 학습합니다. 이러한 과정을 값을 추정, 예측한다는 의미에서 "Model-free prediction"이라 합니다.
이러한 prediction의 유형으로는 Monte-Carlo prediction, Temporal-Difference prediction이 있습니다.
Step2. Model-free control
Optimise the value function of an unknown MDP
두 번째로 agent가 예측한 value fucntion 값을 토대로 value function값이 수렴할 때까지 학습을 반복하여 optimal policy를 도출하고자 합니다. 이러한 과정을 "Model-free control"이라 합니다. 이러한 control 유형으로는 살사(SARSA)와 Q-Learning이 있습니다.
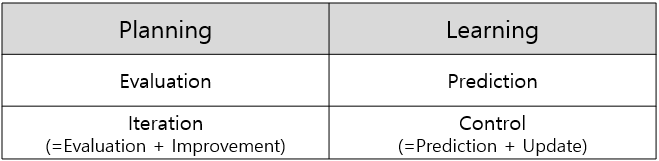
이해를 위해 설명을 덧붙이자면, 앞서 3장에서는 Planning 문제 해결을 위해 Policy와 Value에 대해 Evaluation과 Improvement 과정을 거쳤고, 이 두 과정을 통틀어 문제 해결을 위한 Iteration이라고 칭했습니다. 이를 Learning의 개념과 대응시켜보면 다음과 같습니다. 같은 열에 해당하는 개념이 서로 대응되는 개념이라 할 수 있습니다.
Significance of this lecture
본 chapter와 5장에서 얘기할 prediction과 control 개념은 강화학습 발전의 기반이 된 핵심 개념입니다.
따라서 prediction과 control algorithm을 정확히 이해하고 해당 control의 한계에 대해서도 생각해본다면 오늘 날의 Approximation을 도입한 다양한 강화학습 알고리즘이 고안된 이유와 효용성에 대해서 근본적으로 이해할 수 있을 것입니다.
Outline
본 포스팅에서는 agent의 학습 방법에 차이가 있는 Model-Free Prediction의 2가지 강화학습 알고리즘에 대해서 차례로 다루고, MC와 TD learning algorithm의 장단점과 한계점에 대해 살펴보겠습니다. 마지막으로 강화학습의 전체적인 Unified View에 대해 다루며 포스팅을 마치겠습니다.
1. Monte-Carlo Reinforcement Learning
2. Temporal-Difference Reinforcement Learning
3. Advantages and Disadvantages of MC vs. TD
4. Unified View of Reinforcement Learning
1. Monte-Carlo Reinforcement Learning
Monte-Carlo methods
Monte-Carlo method -줄여서 MC method-가 Learning 문제를 해결하기 위해 접근하는 방법과 특성은 다음과 같습니다.

MC method는 해결하고자 하는 목표를 이뤄낸 "에피소드의 모든 experience"로부터 학습을 진행하고, 이를 complete episodes로부터 학습한다고 표현합니다. 또한 이를 통계학에서 사용하는 용어인 bootstrapping을 활용하여 아래와 같이 표현하기도 합니다.
MC property : No bootstrapping
Bootstrapping이란 통계학 혹은 머신러닝에서 사용되는 개념으로 "무작위 표본 추출에 의존하는 어떤 시험"입니다.
다시 말해, 강화학습에서의 bootstrapping의 특성은 agent를 학습시키는 과정에서 특정 value값을 업데이트할 때 다른 추정값을 사용하는가/사용하지 않는가에 달려 있습니다.
다른 추정값을 사용한다면 bootstrapping, 다른 추정값을 사용하지 않는다면 No bootstrapping으로 구분할 수 있습니다.
Monte-Carlo method의 경우에는 하나의 에피소드가 끝날 때까지 학습을 진행하지 않고, 목표를 달성한 에피소드에 대해서만 학습을 진행하므로 No bootstrapping 특성을 갖는 알고리즘에 해당합니다.
이러한 No bootstrapping의 특성은 강의자료에 빨간색 형광펜으로 표시한 바와 같이 학습에 있어서는 장점보다는 단점에 가까운 특성이라 할 수 있습니다.
EX) No bootstrapping의 단점에 대해서는 이전 포스팅에서 설명드렸던 바둑을 예시로 설명할 수 있습니다.
바둑은 경우의 수가 우주의 원자 수보다 많은 문제입니다. 때문에 문제를 모델링하는 과정에서 첫 번째 state에서 목표로 하는 마지막 state에 달하는데까지. 즉, 하나의 episode에만 많은 연산이 필요합니다. agent의 학습을 위해서는 이러한 episode의 시행이 무수히 많이 필요하므로 No bootstrapping의 특성을 갖는 Monte-Carlo algorithm은 바둑과 같은 매우 복잡한 문제해결에는 적절하지 않습니다.
Monte-Carlo Policy Evaluation
Monte-Carlo Algorithm이 정의한 environment에 대하여 policy evaluation에서의 핵심은 학습을 위해 "Empirical mean return"값을 이용하는 것입니다.
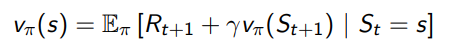
앞선 강의에서 학습한 내용을 상기시켜 봅시다. Bellman Expectation Equation을 활용한 value function은 위와 같습니다. 하지만 여기서 문제가 있습니다. Bellman Expectation Equation의 경우에는 환경의 모델에 해당하는 State transition probability와 환경 전체의 reward를 알아야만 해결할 수 있었습니다. 우리는 환경을 모르는 unknown MDP 문제를 해결하는 것이 목적이기 때문에 이를 모델에 대한 정보 없이 표현할 수 있는 식을 정리할 필요가 있습니다.
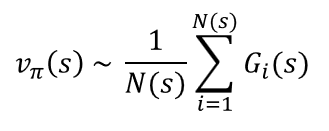
환경을 모르는 Learning 문제해결을 위해서는 사용하는 개념이 2장에서 배운 return이라는 개념입니다.
return을 활용하면 기댓값으로 표현된 value function을 다음과 같이 에피소드를 거쳐온 모든 state의 return의 기댓값으로 표현하여 환경, 모델에 대한 아무런 정보 없이도 에피소드의 history를 활용하여 기댓값을 추정할 수 있습니다. 이러한 value function값의 추정을 Empirical mean return으로 추정한다고 표현합니다.
이해를 돕기 위하여 4개의 state에 대하여 value function값을 추정해보면 아래와 같이 표현할 수 있습니다. 아래 식에서 N(s)은 s라는 state를 여러 에피소드 동안 방문한 총 횟수를 의미하고, G(s)는 그 상태를 방문한 i번째 에피소드에서 state s의 return값입니다.
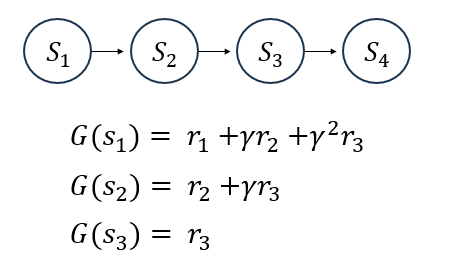
만일 하나의 에피소드가 S1에서 시작하여 S4를 끝으로 에피소드가 끝난다면 각각의 state를 거치는 과정에서 해당 state에 대해 누적된 return값을 위 식과 같이 나타낼 수 있을 것입니다.
이처럼 모든 state에 대하여 여러 번의 에피소드 동안 return값의 데이터가 N(s)번만큼 축적될 것이고, 이를 기댓값으로서 추정하는 방식이 Empirical mean을 활용한 value function의 추정방법입니다.
이러한 Monte-Carlo Policy Evaluation 방식은 하나의 에피소드에 대하여 state에 처음 방문했을 때만 return값을 업데이트할 것인지, 매번 방문할 때마다 업데이트할 것인지에 따라서 아래 2가지로 구분할 수 있습니다.
1. First-Visit Monte-Carlo Policy Evaluation
2. Every-Visit Monte-Carlo Policy Evaluation
First-Visit MC와 Every-Visit MC의 가장 큰 차이점은 계산량에 차이가 있습니다. 각각의 장점에 대해 간단히 설명하자면 First-Visit MC의 경우 agent가 state를 처음으로 방문할 때만 return값을 추정하므로 state와 action간에 단 한 번의 평가만을 수행하므로 계산효율성이 높다고 볼 수 있습니다.
이에 비해 Every-Visit MC의 경우에는 state를 방문할 때마다 return값을 추정하기 때문에 First-Visit MC에 비해서는 계산량이 많지만 추정한 optimal policy에 대한 정확도가 높아질 수 있습니다.
(제가 차후 MC, TD를 실습할 코드에서는 계산 효율의 측면에서 우수한 First-Visit Monte-Carlo 방식을 활용하여 코드를 구현할 예정입니다.)
Then how can we simplify an empirical mean return formula?
하지만 Empirical mean return을 이용한 value function의 추정 방식을 그대로 알고리즘에 적용하기에는 모든 에피소드에 대하여 return값을 state에 각각 계산해야하므로 시간복잡도의 측면에서 한계가 있습니다. 그렇다면 이러한 한계를 어떻게 극복할 수 있을까요?
이는 앞선 포스팅에서 소개드렸던 Dynamic programming을 적용해- Incremental Mean 개념을 활용하여 - return값을 표현하므로써 value function을 간단하게 표현할 수 있습니다.
Incremental Mean
DP를 적용하여 기댓값을 Incremental하게 식을 정리하면 다음과 같습니다.

정리된 맨 아래 식을 살펴보면 한 에피소드가 추가된 mean값 - k개의 에피소드로 추정된 mean값 -은 하나의 에피소드가 추가되기 전. 즉, (k-1)개의 에피소드로 추정된 mean값을 활용하여 위와 같이 표현될 수 있습니다.
Incremental Mean을 활용하여 mean값을 value function으로, x값을 return값으로 대응시켜 MC update를 표현하면 다음과 같이 나타낼 수 있습니다.

위 식에서 alpha값은 Step Size, 학습률로서 value function을 업데이트하는 과정에서 새로운 정보가 기존의 value function값에 얼마나 영향을 미치는지를 결정합니다. Step size값은 목표한 학습 결과를 얻기 위해서는 유연한 조정이 필요한 강화학습에서 아주 중요한 parameter 중 하나입니다.
Step size값이 학습에 미치는 영향
- small step size : 작은 Step size값은 agent가 이전의 정보를 더 신뢰하고 새로운 정보를 덜 신뢰함을 의미합니다. 작은 step size에 따른 학습 결과는 안정적인 학습이 가능하지만 opitmal policy로의 수렴이 느려지게 됩니다.
- big step size : 반대로 step size가 큰 것은 agent가 새로운 정보를 더 신뢰하고 기존의 정보를 덜 신뢰함을 의미합니다. 따라서 optimal policy로의 빠르게 수렴한다는 장점이 있지만, 학습이 불안정하여 목표한 optimal policy로 수렴하지 않고 발산할 수 있다는 단점이 있습니다.
2. Temporal-Difference Reinforcement Learning
Temporal-Difference Learning
다음으로 Temporal-Difference method -줄여서 TD method- 가 Learning 문제해결을 위하여 접근하는 방법과 특성은 다음과 같습니다.

MC method와 마찬가지로 model-free 문제해결을 위하여 에피소드의 experience(history)를 이용하는데, MC method와의 가장 큰 차이점은 TD Learning의 경우 Bootstrapping 특성을 갖는 알고리즘이라는 점입니다. 다시 말해, agent의 학습 과정에서 이전 시점의 value의 추정값을 사용한다는 특징이 있습니다.
두 알고리즘의 차이에 대해서는 아래 슬라이드에서 비교하며 자세하게 설명하고 있습니다.

Monte-Carlo Learning과 Temporal-Difference Learning의 가장 큰 차이점은 업데이트의 목표, update target 에 있습니다.
- Monte-Carlo method의 경우에는 value function을 state에 대해 return값의 기댓값으로 추정하기 때문에 업데이트의 목표가 return, G값에 해당합니다.
- 반면 Temporal-Difference method의 경우에는 value function을 bootstrapping을 활용하여 time step마다 업데이트합니다. 업데이트 목표 역시 총 episode가 끝났을 시에만 계산할 수 있는 return, G값을 목표로 하지 않고, 현재 시간이 t일 때, 한 번의 time step이 지난 시점의 value function값(TD(0))을 업데이트 목표로 학습합니다. 이를 수식으로 나타낸 부분이
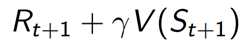
TD learning에서는 학습시키는 식을 표현할 때, 업데이트 목표(t+1)와 현재 시간 t에서의 value값의 차이를 TD error라고 표현합니다. TD error의 식은 아래와 같습니다.
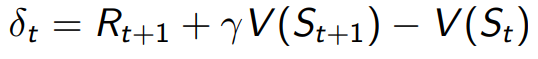
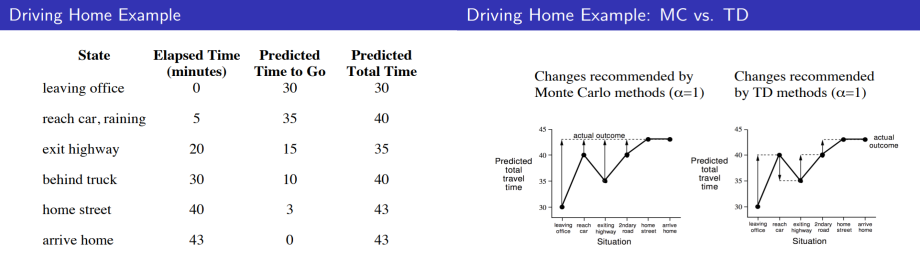
EX) Driving Home Example
이해를 돕기 위하여 간단한 예시를 들어 MC와 TD가 업데이트하려는 목표에 대해 이해해봅시다.
해당 예제는 agent가 office에서 출발하여 집에 도착하기까지의 state를 각각 leaving office를 포함한 6개의 state로 표현하고 각각 상황에 따른 걸린 시간을 학습하는 문제입니다.
오른쪽 그래프에서 MC method 그래프와 TD method의 그래프를 차례로 살펴봅시다.
(이 때, 화살표는 state의 업데이트 목표를 가리킵니다.)
- MC method에서는 하나의 에피소드가 끝난 뒤 각 state에 대한 return값을 업데이트 목표로 삼기 때문에 각각의 state가 가리키는 화살표의 도착 지점이 동일합니다.
- 반면 TD method에 대한 그래프는 업데이트 목표가 다음 State값을 나타내고 있어 각기 다른 업데이트 목표를 가진다는 것을 확인할 수 있습니다.
3. Advantages and Disadvantages of MC vs. TD
마지막으로 위 예시에서 이해한 내용을 바탕으로 Temporal-Difference Method의 장점에 대해서 정리해보겠습니다.

먼저 Monte-Carlo Learning과 Temporal-Difference Learning의 가장 큰 차이점에 대하여 다시 한 번 짚고 넘어가자면, "업데이트 목표 & 업데이트 시점"이라고 말할 수 있습니다.
-
Monte-Carlo Learning의 경우 value function의 업데이트 목표는 state에 대한 return Gt값입니다.
그러므로 업데이트를 위해서는 complete episode를 통해 return값을 계산할 수 있어야 합니다.
따라서 Monte-Carlo Learning은 하나의 에피소드가 끝날 때 업데이트할 수 있습니다. -
반면 Temporal-Difference Learning의 경우 value function의 업데이트 목표는
에 해당합니다. 업데이트 목표는 현재 시간이 time step만큼 지남에 따라서 state별로 달라지게 됩니다. 따라서 Temporal-Difference Learning은 에피소드가 끝날 때까지 기다리지 않고 time step만큼 지났을 때 value function을 업데이트합니다.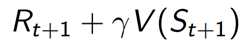
지금까지 간단하게 MC와 TD가 agent를 학습시키는 방법과 시점에 대해 정리해보았습니다.
Q. 그렇다면 incomplete sequence로부터 하나의 에피소드가 끝나지 않더라도 학습시키는 것의 장점은 무엇일까요?
위 질문에 대한 답은 다음과 같습니다.

Temporal-Difference Learning 방식의 경우 step time이 지난 다음 시점에서의 value function값을 업데이트 목표로 삼기 때문에, 추정한 value function값은 결과적으로 low variance의 특성을 보여 보다 신뢰할 만한 estimated value function을 얻을 수 있습니다.
하지만 step time이 지남에 따라서 업데이트한다는 점에서 학습 초기 환경에 대한 initial value값에 추정한 value function값이 민감하게 변할 수 있다는 단점이 있습니다. 이러한 단점은 앞선 TD method의 식에서의 step size값을 유연하게 조정하거나, 학습 목적에 맞는 초기값을 실험적으로 학습하여 찾아내어 해결할 수 있습니다.
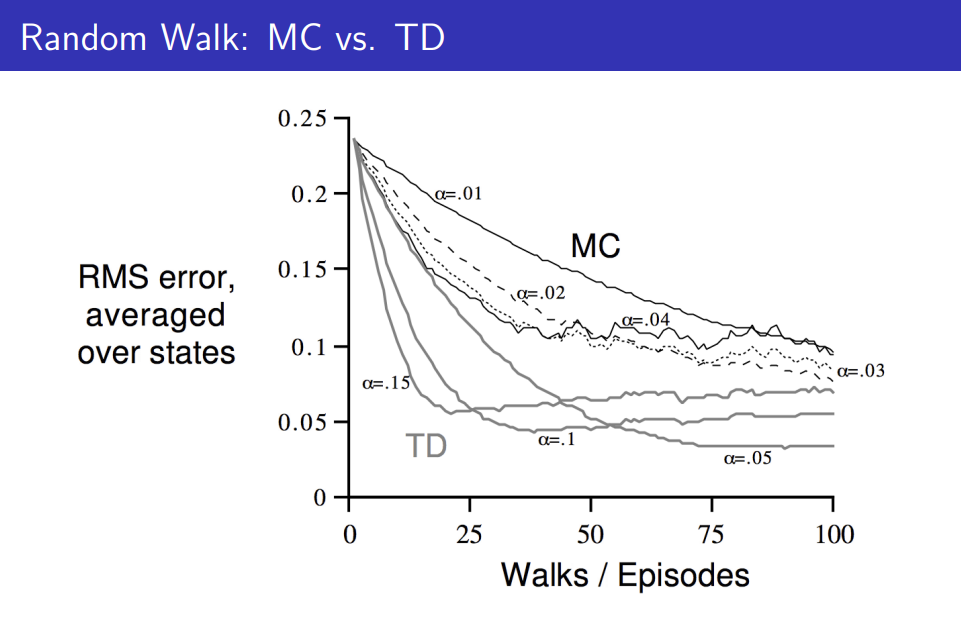
EX) Random Walk 예시 문제에 대한 RMS값의 추이
: 위 문제는 임의의 5개의 state에 대하여 random으로 움직였을 때, 가장 큰 reward값을 얻는 것고자 하는 문제입니다.
위 그래프에서 step size값에 따른 RMS error 그래프의 변화에 주목할 필요가 있습니다.
두 방식 모두 RMS error값이 step size값에 따라서 다르게 나타나는 것을 확인할 수 있습니다.
>>> 따라서 강화학습을 적용하기 위해서는 step size값을 실험적으로 학습시키는 과정을 반복하며 문제해결에 적합한 step size값을 설정하고 그 값을 바탕으로 학습시킬 필요가 있습니다.
4. Unified View of Reinforcement Learning
Comparison of Algorithms using Backup Diagram
지금까지 공부한 Reinforcement Learning의 알고리즘인 Monte-Carlo, Temporal-Difference, Dynammic Programming 각각에 대하여 backup diagram을 살펴보면서, 업데이트 시 sampling이 어떻게 다른지 이해하며 알고리즘을 비교해보고자 합니다.
Backup Diagram of Monte-Carlo Algorithm
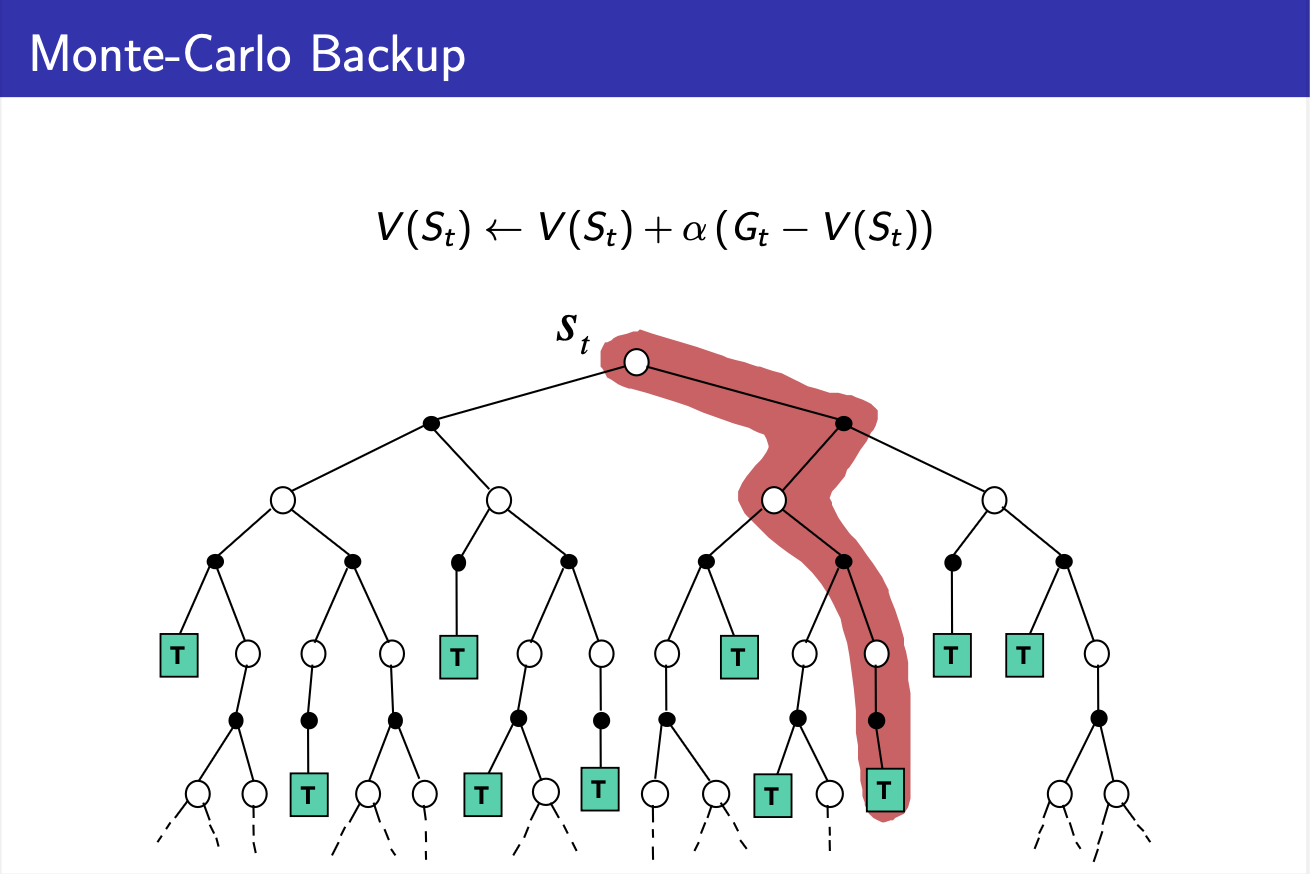
먼저 Monte-Carlo Algorithm입니다. MC의 경우 no bootstrapping 특성을 띄는 알고리즘으로써, 강화학습을 위해서는 하나의 에피소드가 온전히 끝나야만 value function값의 학습이 가능합니다.
따라서 학습 과정에서의 backup은 위와 같이 state 시작점에서부터 에피소드가 끝나는 terminal state까지의 정보를 학습에 이용합니다.
Backup Diagram of Temporal-Difference Algorithm
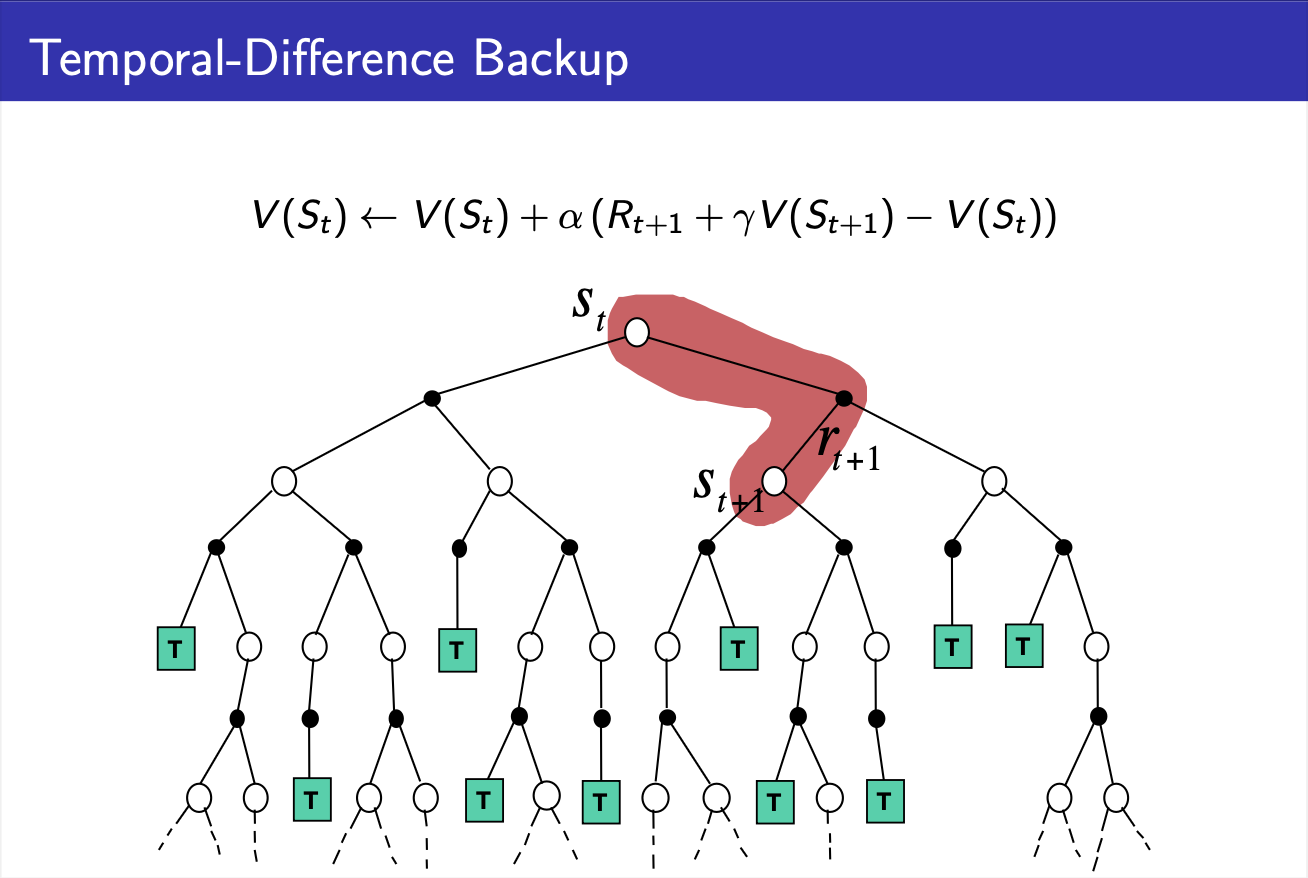
다음으로는 Temporal-Difference Algorithm입니다. TD의 경우에는 MC와 달리 bootstrapping의 특성을 띄는 알고리즘으로, 한 번의 time step이 지난 시점의 value function값(TD(0))을 업데이트 목표로 하여 학습 진행합니다. 따라서 backup diagram을 살펴보시면 업데이트에 관여하는 정보는 현재 시간을 t라고 했을 때, t에서의 state와 (t+1)에서의 state와 reward만이 필요합니다.
MC와 TD algorithm를 bootstrapping의 관점에서 정리하고 넘어가자면
1. MC의 경우에는 시작점의 state에서 에피소드의 마지막 state까지의 정보가 학습에 필요하기 때문에 deep backup에 해당하고,
2. TD의 경우에는 현재 시간 t에 대하여 현재 state와 step 시간이 지난 다음 시간 (t+1)의 state와 reward만이 학습에 필요하므로 shallow backup에 해당합니다.
Backup Diagram of Dynammic Programming
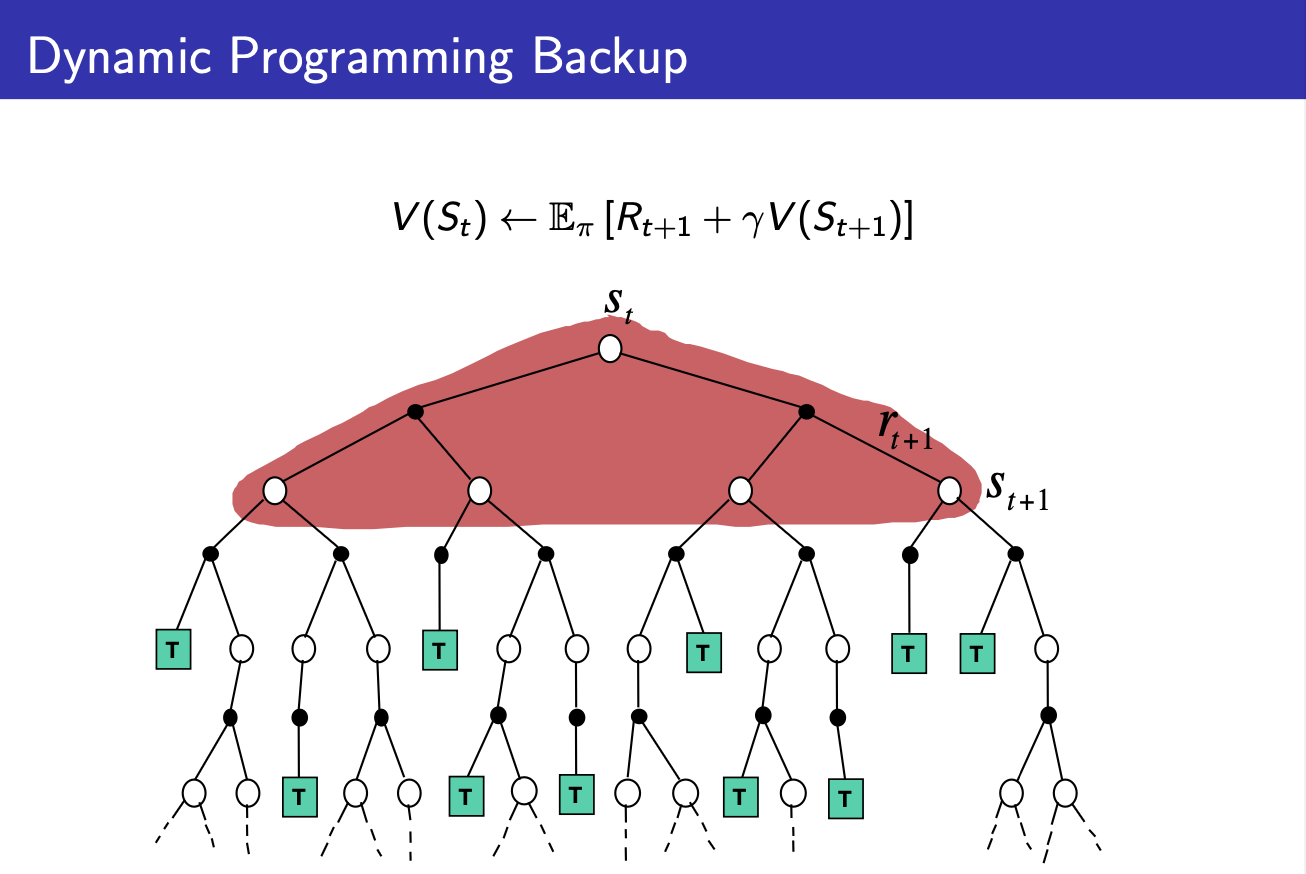
마지막으로 Dynammic Programmng(Policy Iteration, Value Iteration)입니다. DP를 적용한 학습인 Iteration에서는 step 시간에 대하여 시행한 모든 에피소드에 대해 reward와 discount factor를 곱한 value function값의 기댓값을 이용하여 학습을 진행합니다. 따라서 위 그림과 같이 tree에서 모든 step time동안의 모든 state와 reward에 형광펜이 칠해져 있음을 확인할 수 있습니다.
Comparison of MC/TD and DP
MC,TD algorithm과 DP간에 비교하자면 sampling의 관점에서 비교할 수 있습니다.
1. 먼저 MC, TD의 경우에는 단 하나만의 에피소드의 정보를 학습에 사용합니다. 따라서 sample backup의 특성을 갖습니다.
2. 반대로 Dynamic programming은 시행한 모든 에피소드에 대해서 기댓값을 활용하여 학습을 진행하므로 full backup의 특성을 갖습니다.
Unified View of Reinforcement Learning
마지막으로 backup diagram으로 비교한 특성을 바탕으로 MC, TD, DP를 Unified View로 표현한 그림을 설명드리며 포스팅을 마치겠습니다.
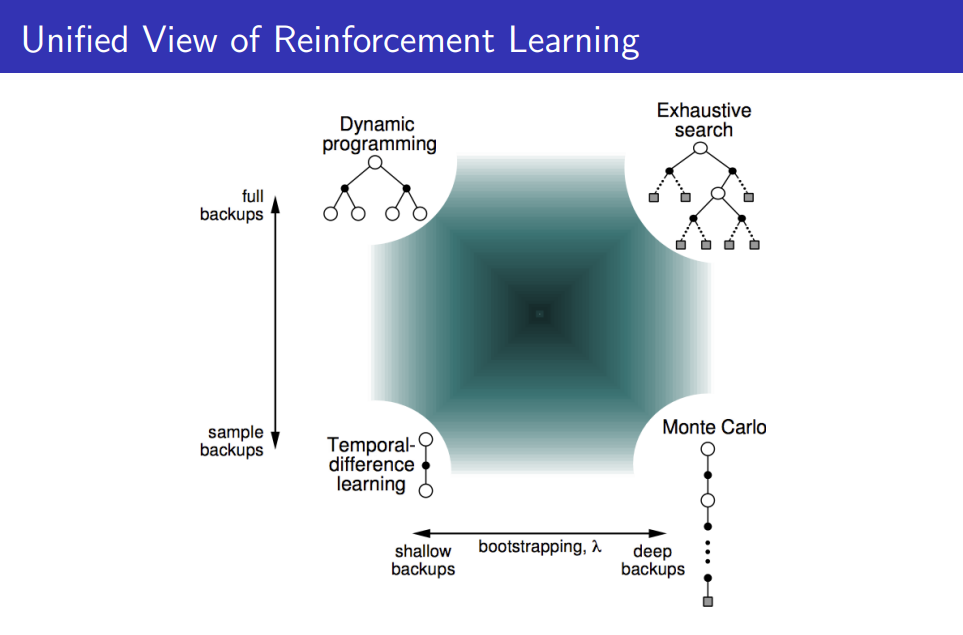
(1) 먼저 MC, TD는 bootstrapping의 특성을 띄는가에 따라서 각각 deep backup와 shallow backup으로 구분됩니다.
이 때, 위 그림에서의 Temporal-Difference algorithm은 오직 한 번의 step time이 지난 시점에서의 정보를 이용해 학습한 TD(0)을 의미합니다.
(* TD의 경우에는 몇 번(n)의 time step을 지나느냐에 따라서 학습에 필요한 state, reward값의 개수가 달라지는데, 이를 일반적으로 n번의 time step을 지날 때까지의 n-step return값을 의미하는 TD(n-1)로 표현합니다. 이러한 time step의 횟수는 학습의 목적에 따라 학습의 효율에 영향을 줄 수 있으므로 적절한 횟수의 설정이 필요합니다.)
(2) 두 번째로 MC/TD와 DP 간의 비교입니다. MC/TD의 경우에는 단 하나의 에피소드 정보를 이용하여 학습을 진행하는 반면, DP의 경우에는 시행한 모든 에피소드에 대하여 정해진 step 시간 동안의 정보를 이용하여 기댓값으로 value function을 학습시킵니다.
1,2에서 bootstrapping 특성의 유무와 backup의 depth의 정도에 따른 강화학습 알고리즘의 분류가 필요한 궁극적인 이유는 시간복잡도를 낮추기 위함에 있습니다.
저희가 강화학습을 적용하고자 하는 문제들은 앞서 예시를 들었던 바둑과 같이 굉장히 복잡한 문제인데, 이러한 문제를 모든 state에 대하여 학습시키기에는 - 그림에서는 Exhaustive search를 이용한 학습방법을 의미합니다. - 분명한 한계가 있고 현실적으로 일반적인 사항의 컴퓨터로는 계산할 수 없는 경우가 많습니다.
EX) 바둑은 단 40수에 대해서만 학습을 시킨다고 하더라도 학습에 필요한 game state값이 천문학적인 수준에 달합니다.
>>> 따라서 저희가 관심 있게 살펴보아야 할 부분은 시간복잡도가 작은 sample backup에 해당하는 알고리즘 - Monte-Carlo Algorithm, Temporal-Difference Algorithm -입니다.
그리고 sample backup으로 분류되는 알고리즘 안에서도 업데이트 시에 결정한 time step수(n)에 따라서 bootstrapping 정도에 차이가 있습니다. 이를 그래프로 나타내면 다음과 같습니다.
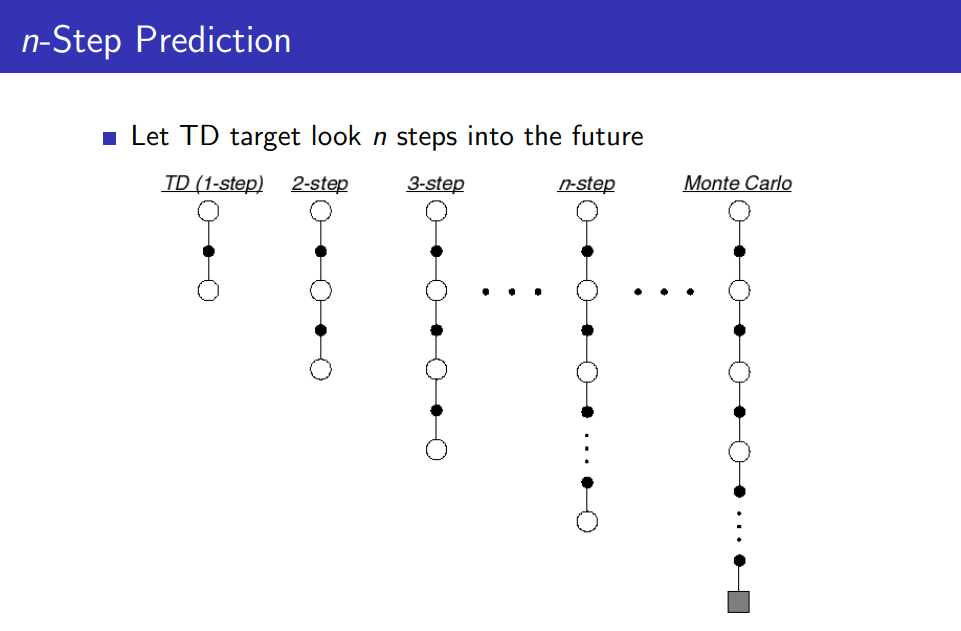
위의 그림은 n-Step에 따른 Temporal Difference target를 표현한 그래프입니다.
- n = 1일 때, 일반적인 Temporal Difference learning에 해당합니다.
- n = INF(무한)일 때, 처음 state에서 시작하여 가장 마지막 terminal state에 도착할 때까지의 TD를 targetting한다는 의미이므로 Monte-Carlo learning을 의미하게 됩니다.
이를 수식으로 표현하면 다음과 같습니다.

업데이트 목표_update target에 해당하는 n-step return은 n값에 따라 n = 1일 때는 TD, n = INF일 때는 MC에 해당하여 Gt(INF)는 일반적인 return을 의미합니다.
Preview of next posting
지금까지 unknown MDP 문제해결을 위한 Learning Algorithms으로 Monte-Carlo Algorithm과 Temporal-Difference Algorithm의 학습방법에 대해서 공부했습니다.
다음 포스팅에서는 Grid World 환경에서 정의한 심플한 문제를 MC, TD를 적용하여 MATLAB 코드로 구현하고 코드를 리뷰할 계획입니다.
* Reference
Lecture4 강의자료 : https://www.davidsilver.uk/teaching/
Policy Evaluation/Improvement & Value Iteration image : 이웅원, 양혁렬, 김건우, 이영무, 이의령 지음, 『파이썬과 케라스로 배우는 강화학습』, 위키북스 p.118, 119
Bootstrapping : https://ko.wikipedia.org/wiki/%EB%B6%80%ED%8A%B8%EC%8A%A4%ED%8A%B8%EB%9E%A9_(%ED%86%B5%EA%B3%84%ED%95%99)