10. Backtracking(DFS)

🧩 N-Queens 문제

📘 문제 설명

• 8-Queens의 경우 경우의 수는 $64^8$, 완전탐색 불가
• State-space tree 또는 search-space tree로 모델링 가능
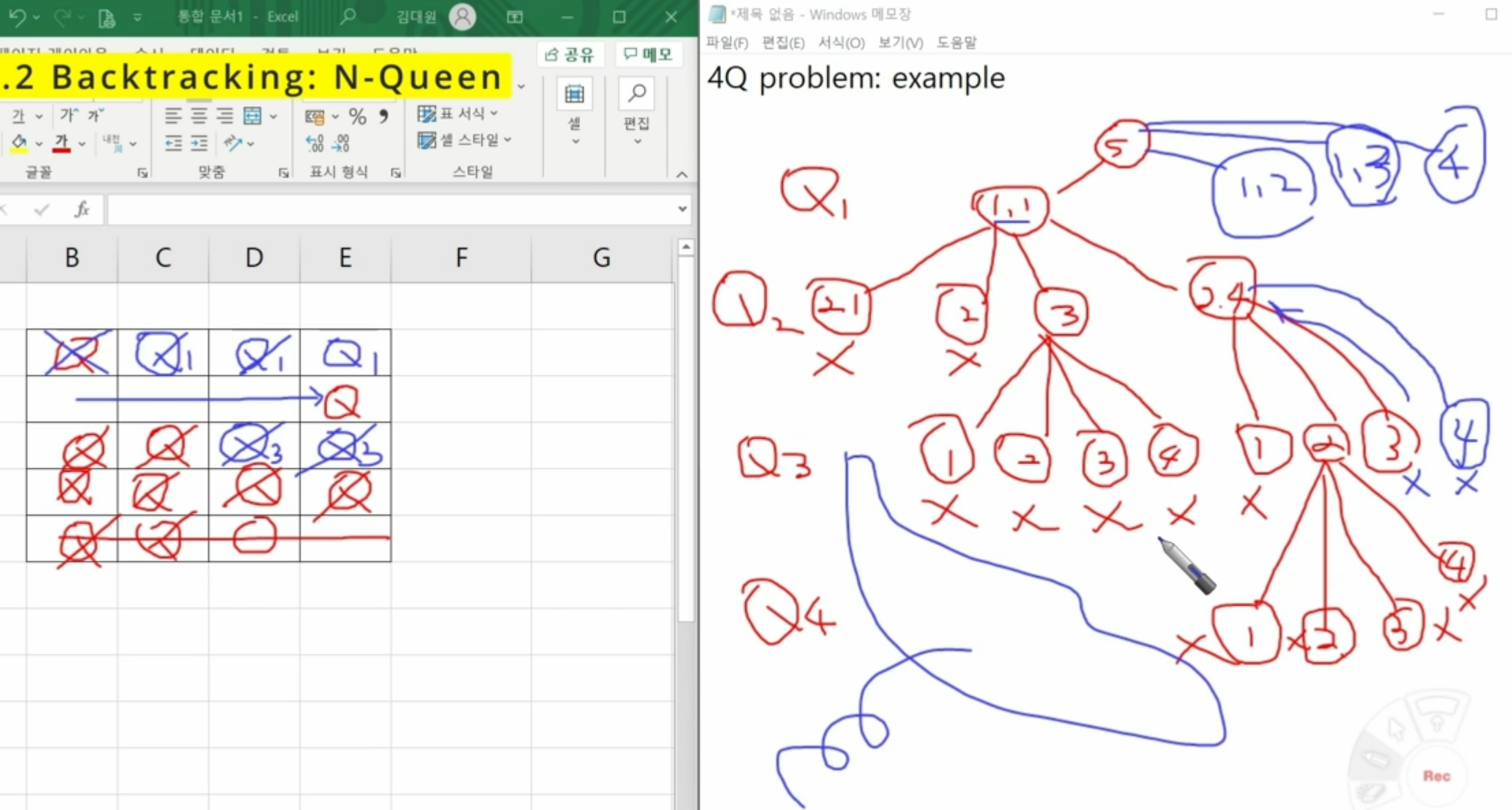
• 예: 4-Queens → 4단계 트리 구조로 표현

💡 핵심 아이디어

• 모든 조합을 다 확인할 필요는 없음
• 백트래킹을 통해 불필요한 경로를 미리 제거

🔁 Backtracking 구성

1. DFS 방식으로 상태 공간 트리 탐색
   → 단, promising한 경우만 진행
   → 같은 행/열/대각선에 퀸이 있으면 skip

2. Non-promising → backtrack (되돌아가기)
   → 가지치기(pruning) 수행

3. 각 노드에서 promising 여부 확인 → 아니면 부모 노드로 backtrack

🎨 설계 관점

• Promising function 설계가 핵심
• N-Queen 문제는 유망함을 판단하는 함수가 명확히 주어짐
• DP나 이항계수 문제는 recurrence relation(점화식)이 주어짐

🧠 분석 관점

• 최적성: 답이 있으면 반드시 찾음 (자명)
• Time Complexity: 지수시간 (EXP)
• 중요성: 이론보다 실제 실행 시간 성능이 중요

---

🎯 Subset Sum Problem

📘 문제 정의

• 0/1 Knapsack의 특수한 형태
• 아이템 집합 $S = \{item_1, ..., item_n\}$
• 무게: $w = \{w_1, ..., w_n\}$
• 목표: 무게 합이 정확히 $W$인 부분집합 $A$ 찾기

🟨 Backtracking for Subset Sum Problem

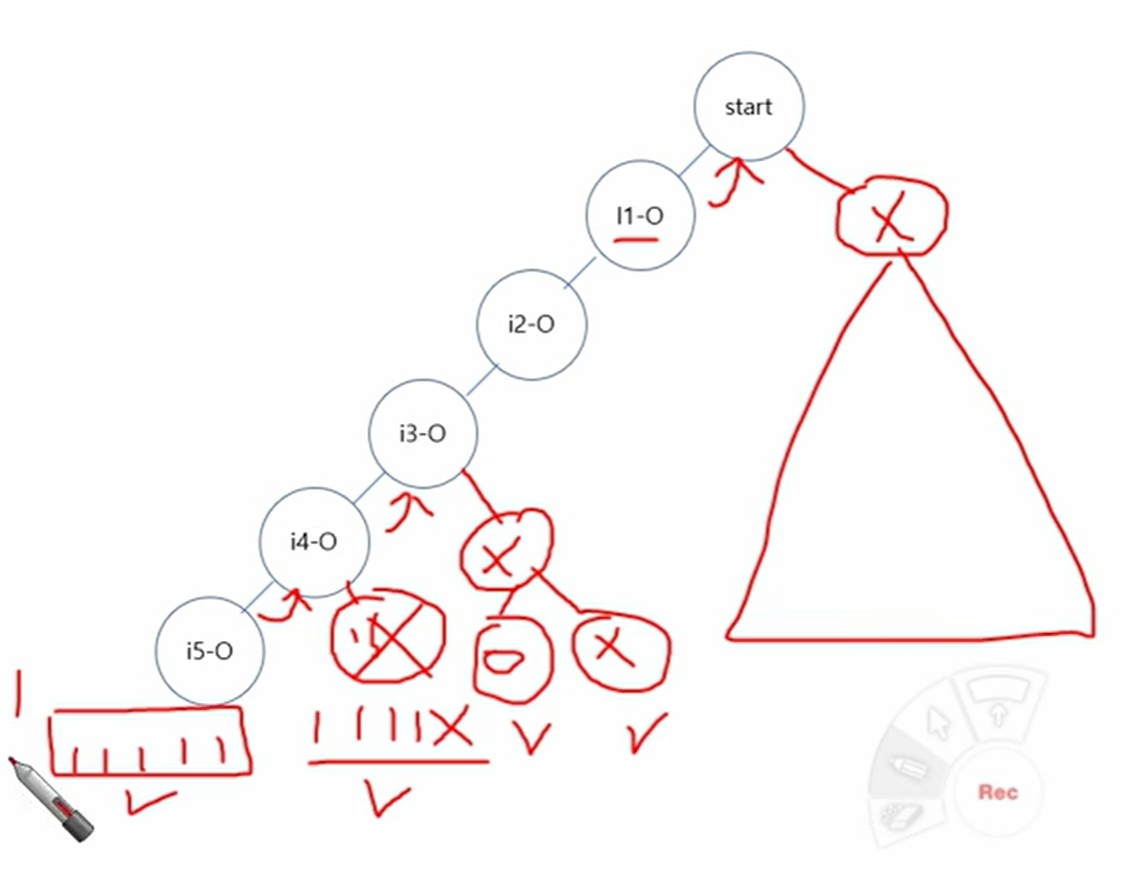
Step 1: promising function 설계

1. i-th level:
   현재까지의 weight + 다음 weight(i+1) > W 이면 더 진행할 수 없으므로 STOP
   
   
2. weight + 미래 총 weight 합 < W 이면
   > 아무리 더해도 목표 weight W에 도달 못하므로 STOP

→ 즉, 두 조건 중 하나라도 만족하면, 해당 노드는 유망(promising)하지 않으므로 탐색 중지

---

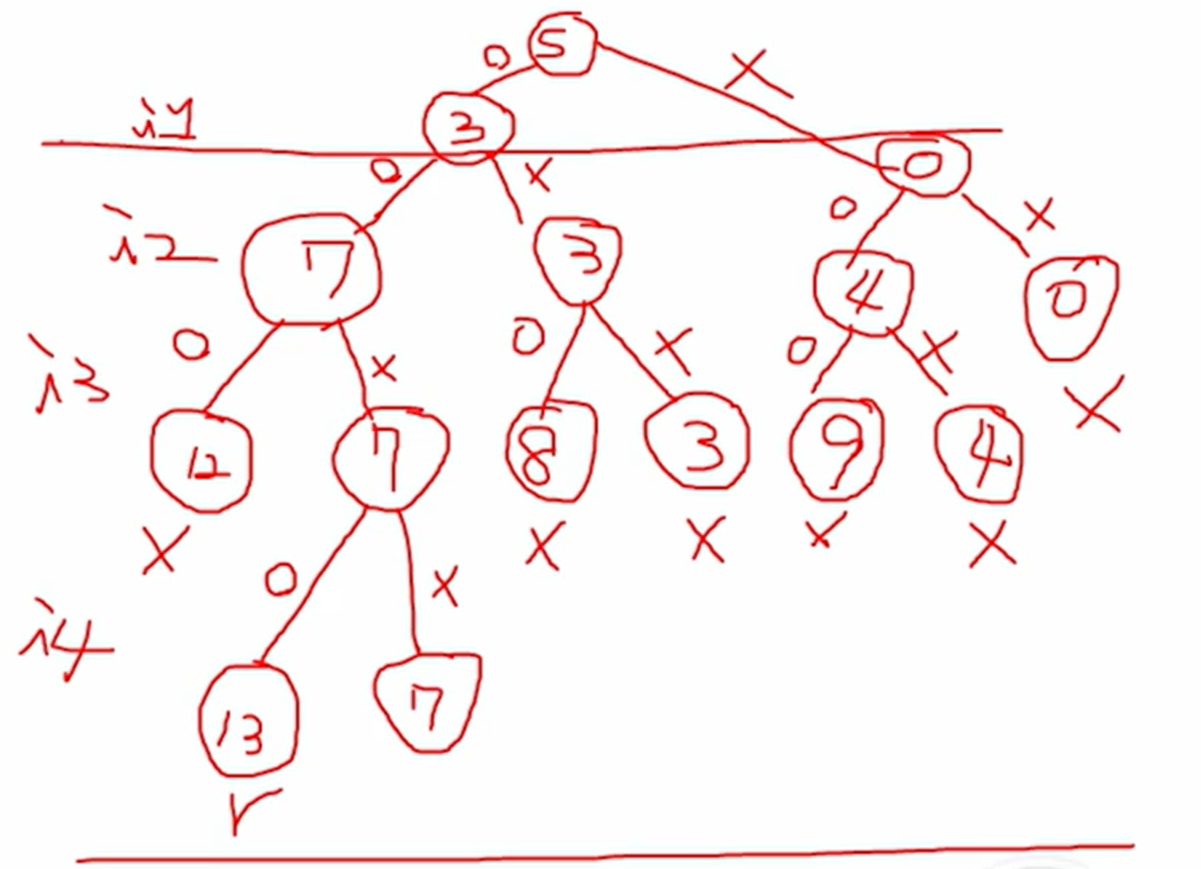
🔹 예제 (Example)

• n = 4
• w_i = (3kg, 4kg, 5kg, 6kg)
• W = 13kg

이건 Subset Sum 문제로, 총 무게가 13kg이 되는 부분 집합을 찾는 문제예요.

---

필요하시면 이 예제로 백트래킹 트리도 그려드릴 수 있어요.

🎮 응용 적용 기술

게임 서버

🔍 알고리즘

• Brute-force: 모든 부분집합 탐색
• DFS 기반 재귀 탐색 사용

🍧 Backtracking 전략

• Promising function 설계
• DFS 방식으로 선택/비선택 분기하며 탐색

---

📊 분석

• Optimal solution 보장
• 성능: promising function의 품질에 따라 달라짐
  예: $15/31$ 노드 생성 → 가지치기 효과 확인

❓ 교수 질문

• 아이템이 정렬되어 있으면 더 빠른가?
• 정렬이 탐색 효율에 긍정적이면, 정렬 후 탐색하는 게 유리
  → 약간의 정렬 비용은 감수할 가치 있음

---

🎨 Graph Coloring Problem

📘 문제 정의

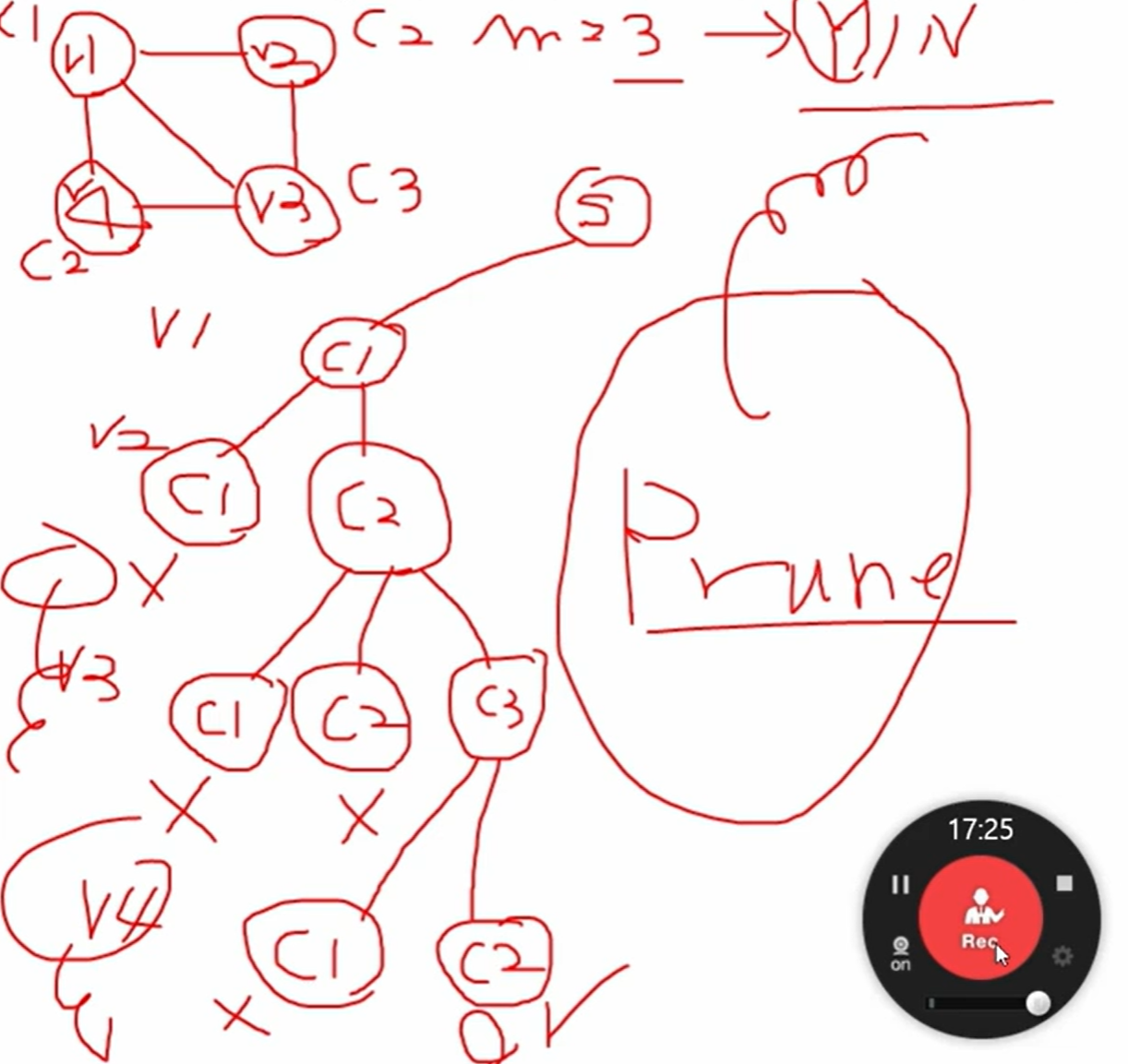
• Vertex Coloring (또는 m-Coloring) 문제
• 인접 정점은 서로 다른 색으로 칠해야 함
• 목표: 그래프를 m개의 색으로 coloring 가능한가?

🔍 조건

• 정점 수 $n$, 색 수 $m$

📊 복잡도

• Brute-force: $O(m^n)$
  → 모든 정점에 모든 색 조합 시도

❓ 교수 질문

1. 최소 m은 어떻게 찾나? → 불가능 (NP-hard)
2. m이 주어졌을 때 coloring 가능한가? → 가능 (백트래킹)

✅ 해결 방법: Backtracking

• Promising function: 인접 노드에 같은 색 있으면 STOP

---

🧭 Hamiltonian Circuits (HC) Problem

📘 정의

• Hamiltonian Path / Cycle 포함
• 출발 노드에서 시작, 모든 정점 1회씩 방문, 다시 출발 노드로 복귀
  

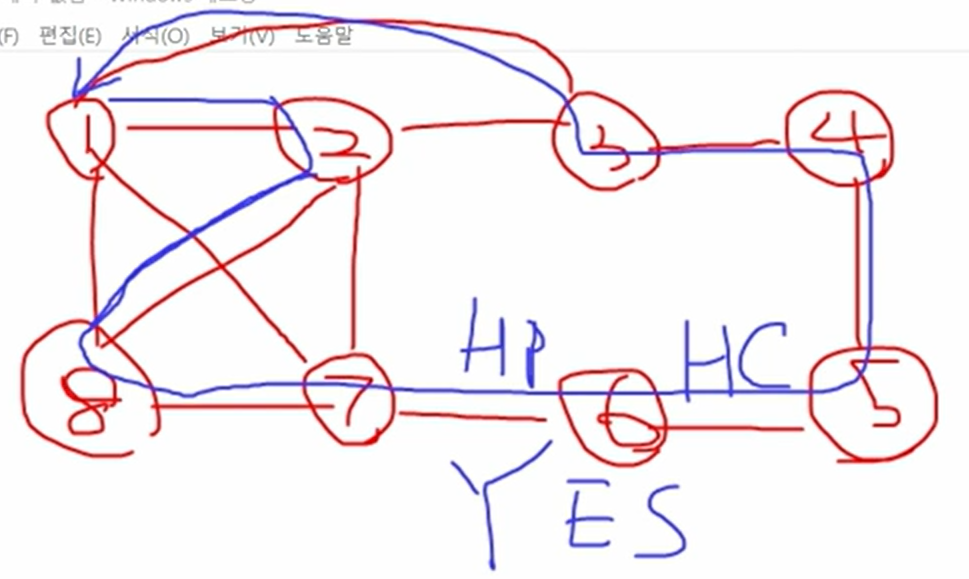
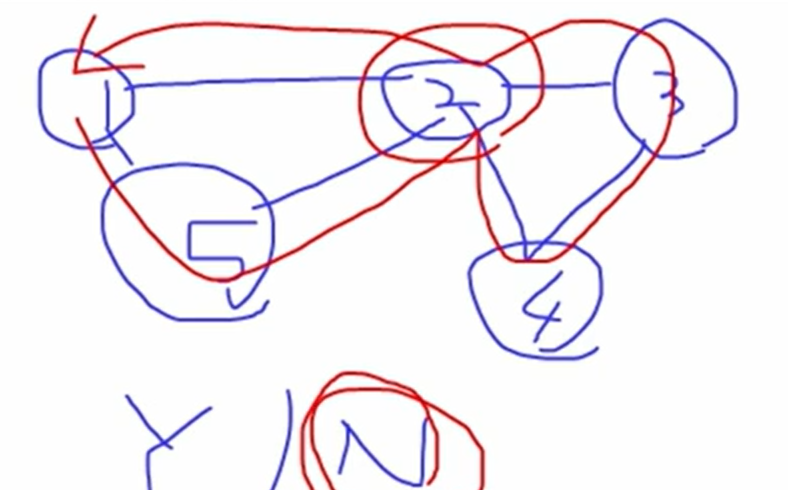
🔍 Promising 조건

1. $i$번째 노드 → $(i+1)$번째 노드로 이동 가능해야 함
2. $(n-1)$번째 노드는 0번 노드로 돌아와야 함
3. 이미 방문한 노드는 다시 방문 불가

---

🧠 분석

• Brute-force 복잡도: $O(n!)$
• 백트래킹에서는 생성된 노드 수와 실행 시간이 주요 성능 지표