9. Knapsnack problem

지드래곤드래밥·2025년 6월 16일

알고리즘

목록 보기

1/7

🎓 Greedy Algorithm & Knapsack Problem

❓ Why is Greedy Algorithm Important?

단순하고 빠르며 구현이 쉬움
- 자연스러운 휴리스틱 기반
- 직관적이라 첫 접근으로 많이 사용됨
기준점 역할
- 새로운 문제에서 baseline으로 사용
- 정밀도/속도/자원 효율성 비교에 유용
일부 문제에서 Optimal Solution 가능
- 단, local optimal → global optimal 이 되기 위해선 증명 필요

🎒 Knapsack Problem 설명

예시 1: 도둑 가방

각 아이템의 무게와 이익 다름
일부만 담을 수 있음 (무게 제한 존재)
목표: 어떤 조합이 최대 이익?

예시 2: 스타트업 투자

예산 한도 내 여러 투자 대상
어떤 투자 조합이 수익 극대화?

📐 문제 정의

아이템 집합 $S = \{item_1, ..., item_n\}$
무게 $w_i$ , 이익 $p_i$
배낭 용량 $W$

목표:

$\sum p_i$ 최대
단, $\sum w_i \leq W$

🤔 알고리즘 비교

방식	설명	복잡도
Brute-force	모든 조합 탐색	$O(2^n)$
Divide & Conquer	최적 분할 여부에 따라 달림	-
Dynamic Programming	최적 부분 구조 활용	$O(nW)$
Greedy	빠르지만 최적 보장 안 됨	$O(n \log n)$ (정렬 포함)

⚠️ Greedy 알고리즘 한계 예시

예제 1: 그냥 값이 가장 큰거 고르기 → 🙁

w = [25, 10, 10]
p = [10, 9, 9]
W = 30

Greedy 선택: item_1 (가치 10)
Optimal: item_2 + item_3 → 가치 18 ✅
→ ❌ Greedy 실패

예제 2: 단위 무게당 가치 기준 → 🙁

w = [5, 10, 20]
p = [50, 60, 140]
W = 30

단위이익:
item1 = 10, item2 = 6, item3 = 7
Greedy 선택: item1 + item3 → $190
Optimal: item2 + item3 → $200 ✅
→ ❌ again, Greedy fails

🔍 Q: 0/1 Knapsack(쪼갤 수 없음)을 어떻게 푸는가?

Brute Force (BF): 2ⁿ개의 조합 다 검사 (시간 너무 큼)
Divide and Conquer (D&C): 최적해 가능하지만 비효율적
Dynamic Programming (DP): ✅ 일반적으로 가장 좋은 방법
Greedy: 일반적으로 ❌ 최적해 보장 안 됨

❓언제 Greedy가 최적해를 제공하나?

0/1 Knapsack에서는 일반적으로 ❌
하지만 Fractional Knapsack(아이템 쪼갤 수 있는 경우)에서는 ✅ Greedy가 최적

→ 예: 남은 공간 5kg이면 item₂를 5kg만큼 잘라서 넣을 수 있음

✅ DP로 해결하기

0/1 Knapsack 문제를 DP(동적 계획법)으로 푸는 방식 – 점화식(recurrence equation)

✅ Q: DP의 핵심 – 최적 부분 구조(optimal substructure)가 있는가?

원리의 이름: 최적성의 원리 (Principle of Optimality) → YES
즉, 국소적인 하위 문제(Local subproblems)의 최적해를 통해 전체(Global) 최적해를 구할 수 있음
과제(HW): 이 원리가 왜 성립하는지 교과서에서 설명 보기

Knapsack 문제는 각 단계의 결정이 독립적이기 때문에, 이전 단계에서의 최적해가 이후 단계의 최적해에 영향을 주지 않습니다. 따라서 전체 문제의 최적해는 그 하위 문제들의 최적해로 구성될 수 있으며, 이는 곧 최적 부분 구조(Optimal Substructure)가 성립함을 의미합니다.

후보1: 1차원 배열을 사용하는 방식

상태: 아이템을 담거나 담지 않았을 때의 **누적 이익(profit)**을 저장.
P[i]: i번째 아이템까지 고려한 상태에서의 누적 최대 이익

예시

P[i] = max(1) P[i-1] or 2) P[i-1] + p_i
→ ❌ 잘못된 접근
→ 이유: 무게 고려가 없다!

후보2: 2차원 배열을 사용하는 방식 (아이템, 무게 기준)

P[i][w] = i번째 아이템까지 고려했을 때, 무게 w 이하로 담을 수 있는 최대 이익

두 경우 고려:

item_i를 못 담는 경우
item_i를 담는 경우 (→ 남은 무게에 담을 수 있음)

⛔ 잘못된 점화식

P[i][w] = max(
    1) P[i-1][w],
    2) P[i-1][w] + p_i
)

→ ❌ 틀림!
→ 이유: item_i를 담으려면 그 전 무게가 w - w_i 만큼 비어 있어야 함

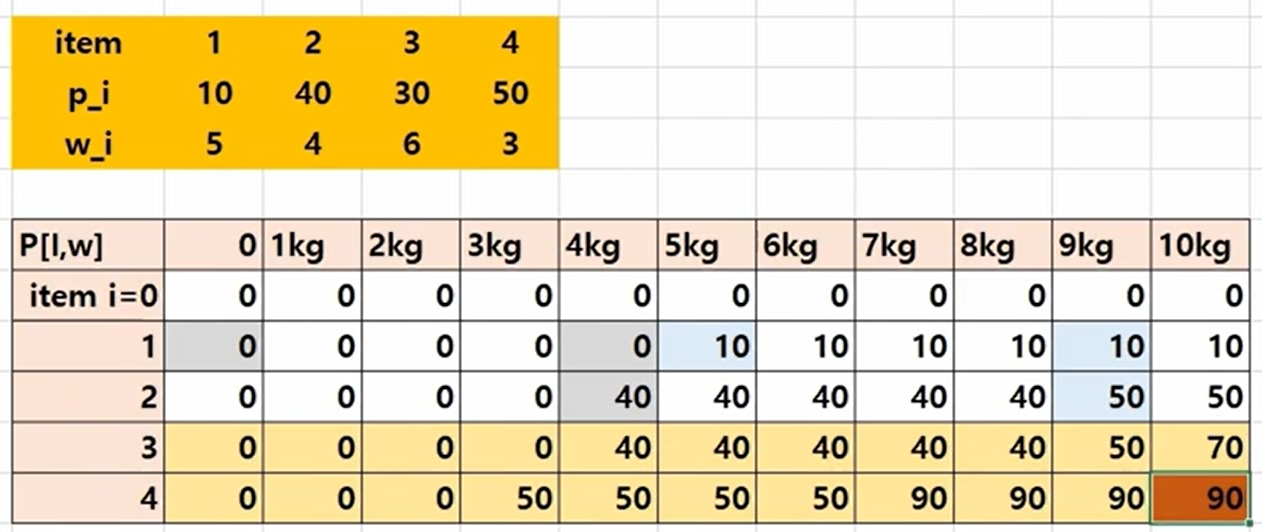
✅ 최종 정답 점화식 (Final)

P[i][w] = max(
    1) P[i-1][w],
    2) P[i-1][w - w_i] + p_i   // item_i 선택한 경우
)

⏱️ 시간 복잡도

O(nW) (n: 아이템 수, W: 배낭 용량)
단, W가 클 경우 → Pseudo-polynomial
→ 입력 "값" 크기에 따라 시간 증가

⏱️ DP 시간 복잡도

O(nW) (n: 아이템 수, W: 배낭 용량)
단, W가 매우 크면 → Pseudo-polynomial
→ 입력 "크기"가 아닌 입력값의 범위에 따라 시간 증가

❗ 그런데 실제로 느린 이유는?

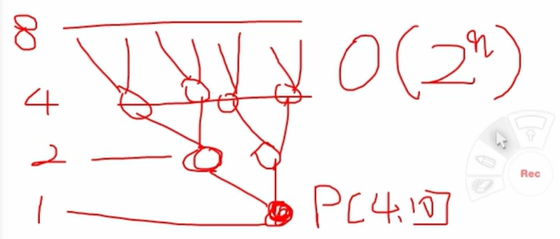
operations = 1 + 2 + 2² + ... + 2^(n-1)
           = 2^n - 1 ≈ O(2^n)

➡️ 결국 Brute-force와 같은 수준의 계산량 발생

❓ Q: 왜 이런 일이 벌어질까?

문제 자체가 매우 어렵기 때문
Knapsack 문제는 NP-Hard
→ 구조적으로 탐색 공간이 폭발함

🔥 핵심 정리

Greedy: 빠르지만 최적 보장 못 함
DP: 느릴 수 있으나 항상 최적 보장
문제 성격에 따라 알고리즘 선택 중요
Knapsack은 대표적인 NP-hard 문제임

...

지드래곤드래밥

다음 포스트