🧩 문제 상황:
- TSP(외판원 문제)에 도시가 1 ZB(10²¹)개나 있음
- Knapsack 문제에서 아이템이 1만 개 있음
- Google의 데이터가 30PB → 계산 불가능(computationally prohibited)
❗️문제: NP 문제처럼 효율적인 알고리즘을 못 찾는 경우는?
선택지는 3가지:
-
느리지만 정확한 알고리즘 → 사용 불가
-
최적해를 포기 → 근사해(approximate solution)를 선택
- 🌟 그래서 나온 게: Approximation Algorithm (새로운 설계/분석 필요)
-
병렬화(Parallelization)
- 슈퍼컴, GPU, 분산 시스템을 이용한 병렬 알고리즘
📌 결론 요약:
| 상황 | 대응 방식 |
|---|---|
| NP 문제로 최적해 못 구함 | 근사 알고리즘 설계 |
| 계산 시간 너무 큼 | 병렬화로 속도 개선 |
| 설계로 해결 안됨 | 문제 자체의 복잡도 이론 분석 |
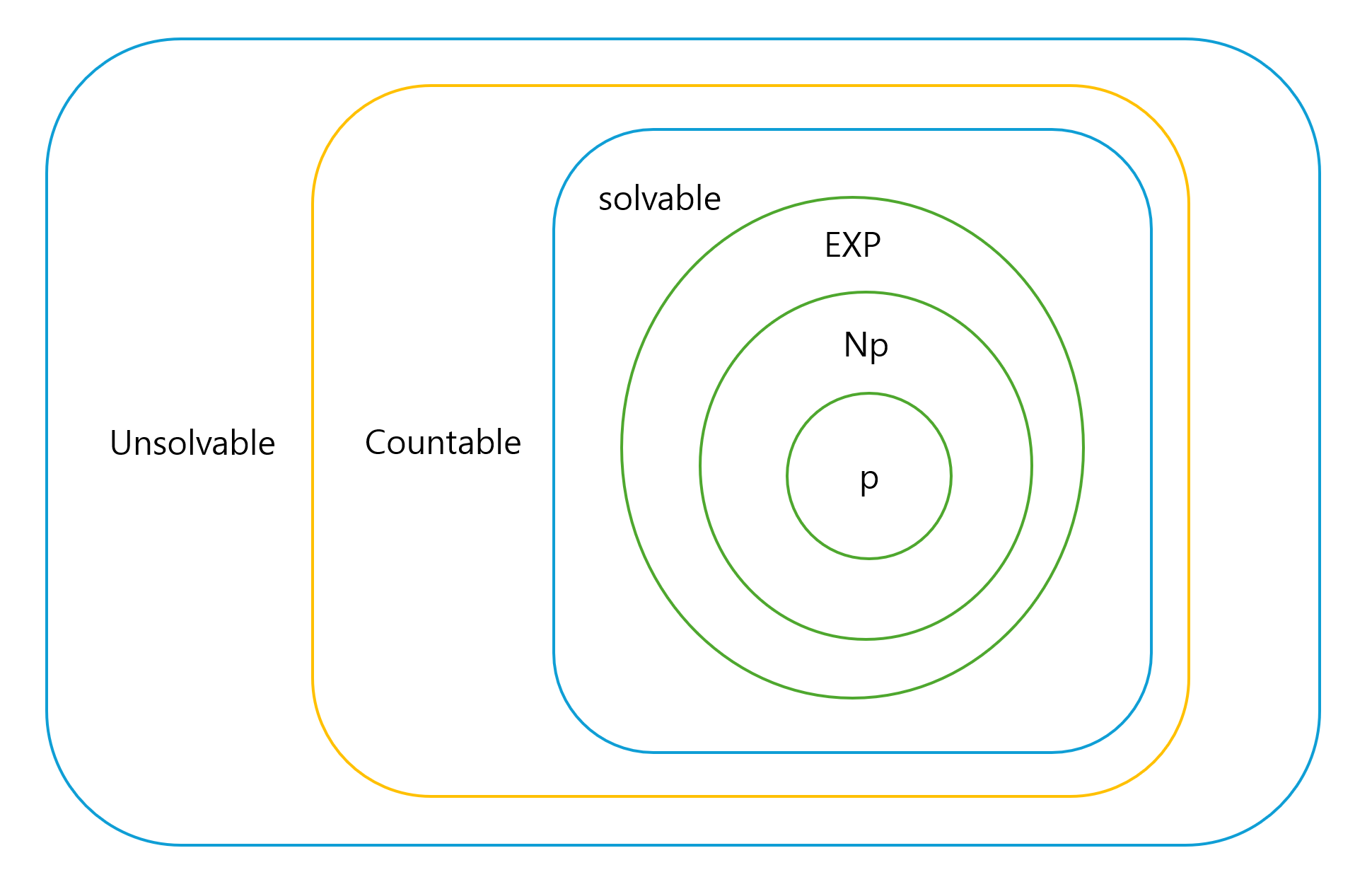
🔵 Unsolvable (해결 불가 문제들)
🟡 Countable (셀 수 있는 문제들)
🔵 Solvable (계산 가능 문제들)
🟢 P (다항 시간 해결 가능 문제)
🟢 NP (다항 시간 검증 가능 문제)
🟢 EXP (지수 시간 해결 문제)
🔷 강의 주제:
Theory of Computation 과목의 핵심은 문제들을 계산 복잡도 관점에서 분류하는 것.
"P ⊆ NP ⊆ EXP ⊆ Solvable ⊆ Countable"
🟡 Countable Problems (셀 수 있는 문제들)
Q1. 0과 10 사이의 정수 개수?
→ Finite countable
Q2. 0과 10 사이의 실수 개수?
→ Uncountable (→ 오답: infinite countable ❌)
Q3. 0과 무한대 사이의 정수 개수?
→ Countably infinite
Q4. 0과 1 사이의 실수 개수 > 0과 10 사이의 정수 개수인가?
→ Yes (실수가 더 많음)
🔷 문제 난이도 비교 예시
Q. 정렬 문제(Sorting, P)는 배낭 문제(Knapsack, NP)보다 쉬운가?
→ **문제의 난이도 클래스(P/NP)**를 분석하여 설계하고 증명해야 함
→ ⇒ proper design/analysis 가 필요
👻 기말 시험 예시 답안 힌트
- I can not find a poly.time algorithm → 이 문제는 P에 속하지 않음, 설계 불가능
- I found EXP algorithm for this problem → EXP 클래스에 속함, 시간이 오래 걸림
✅ P-Class vs NP-Class
🔷 Easy vs Intractable 문제 비교
-
Easy problem
- 좋은 알고리즘 존재
- 시간 복잡도: polynomial time (다항 시간)
-
Intractable problem
- 이론상 풀 수는 있지만, 다항 시간(poly-time) 알고리즘이 없는 문제
- 즉, 계산량이 너무 많아서 현실적이지 않은 문제들
공식 정의
-
P-class
- 결정 문제(decision problem) 중
- 시간 복잡도 **T(n)**이 다항식인 문제
- Poly time 안에 해결 가능
-
EXP-class
- 지수 시간 안에 해결 가능 (Exponential Time)
😸 1. P-class에 속하는 문제들 (쉬운 문제들)
-
예시: 정렬(Sort), 탐색(Search), 최단경로(Dijkstra) 등
-
특징:
- 효율적인 알고리즘 존재
- 다항 시간에 풀림 (Polynomial time)
- Tractable (현실적으로 풀 수 있음)
-
요약: Fast, efficient, optimal
😼 2. P-class에 속하지 않는 문제들 (Intractable)
-
예시:
O(n^2)불가,O(n!)은 가능 → 브루트포스만 가능- 모든 Hamiltonian path 찾기:
O(n!)필요
-
특징:
- 알고리즘은 존재하지만 시간 복잡도가 너무 큼
- 현실적으로 풀 수 없음
- Intractable = 이론적으론 풀 수 있어도 비현실적인 시간 소요
🙀 3. P도 아니고 Intractable도 아닌 문제들
-
예시: Knapsack, TSP, Graph Coloring, Subset Sum
-
NP-class에 속함
-
이 문제들은 아직:
- P인지 아닌지 모름
- Intractable인지 확정 안 됨
-
중요한 이유:
→ 미래에 효율적 알고리즘이 발견될 수도 있음
⚠️ Halting Problem (정지 문제)
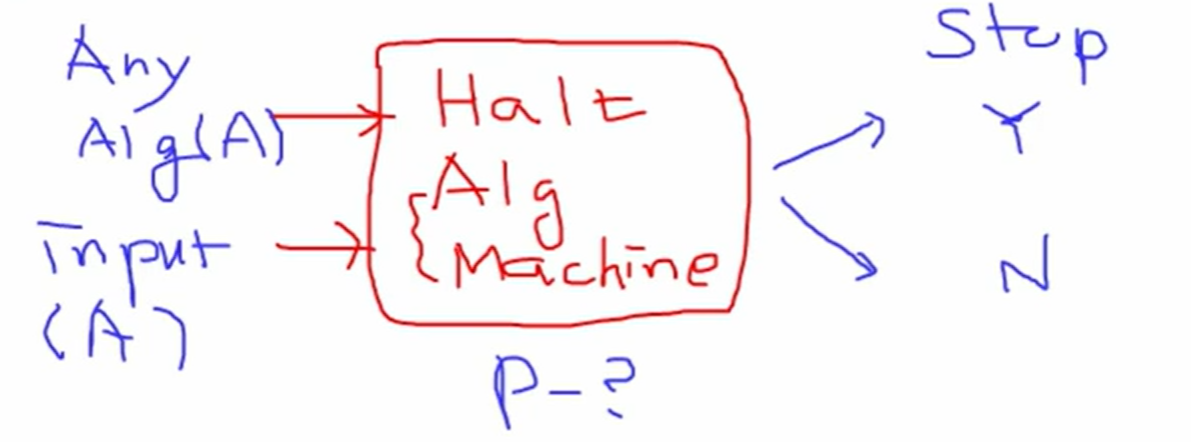
- 문제: 어떤 알고리즘이 주어진 입력에서 정지할지 아닐지 판단 가능할까?
- 답: 불가능하다 (해결 불가 문제)
- P-class 아님, Uncomputable
- 컴퓨터 과학에서 처음 증명된 비결정 문제
🔑 핵심 요약
| 분류 | 설명 | 예시 |
|---|---|---|
| P-class | 빠르게 풀 수 있음 | Sort, Search, Dijkstra |
| Intractable | 풀 수는 있지만 시간 너무 많이 걸림 | Hamiltonian Path |
| NP-class (미정) | 풀기 쉬운지 어려운지 아직 모름 | TSP, Knapsack |
| Uncomputable | 아예 풀 수 없음 | Halting Problem |
✅ NP 정의
-
NP (Nondeterministic Polynomial time)는 다음을 만족하는 결정 문제(decision problem)들의 집합:
- 주어진 해(solution)가 정답인지 다항 시간 안에 확인할 수 있는 문제들
- 정답을 맞췄는지 검사하는 건 쉽지만, 그 정답을 찾는 건 어려울 수 있다
✅ 핵심 요약
- NP 문제는 빠르게 검증은 가능하지만, 빠르게 푸는 알고리즘은 아직 모름
- 전제: 해(solution)가 주어졌다고 가정하고 시작
🔶 대표적인 NP 문제들 (모두 최적화 문제 vs 결정 문제로 표현됨)
1. TSP (Traveling Salesman Problem)
-
최적화 문제 (Optimization): 가장 짧은 경로 찾기 (optimal tour)
-
결정 문제 (Decision):
- 예: “모든 도시를 방문하고 돌아오는 경로가 cost < 200인 경로가 있는가?”
- 답: Y/N
-
질문: TSP는 P에 속하는가? NP에 속하는가?
2. Knapsack Problem
-
최적화 버전: 제한된 무게 내에서 최대 이익(profit)을 얻는 아이템 조합 찾기
-
결정 문제:
- 예: “이익이 100을 초과하는 아이템 집합 A가 존재하는가?”
- 답: Y/N
3. Graph Coloring
-
최적화 문제: 최소 색상 수로 그래프 색칠
-
결정 문제:
- 예: “이 그래프를 m가지 색으로 색칠할 수 있는가?”
- 답: Y/N
- backtracking 알고리즘 예시로 해결 시도 가능
4. Clique Problem
-
정의: 그래프 내의 완전 부분 그래프 (모든 정점이 서로 연결된 집합)
-
용도: Bioinformatics, SNS 분석 등
-
예시: clique size가 4인 부분 그래프(파란색), size=3 (초록색)
-
최적화 문제: 최대 clique 찾기
-
결정 문제:
- 예: “크기 k 이상의 clique가 존재하는가?”
- 답: Y/N
