14. NP

🔹 NP란 무엇인가?

👕 정의 요약

• NP는 결정 문제(Decision Problems) 중에서,
  주어진 해가 맞는지 여부를 다항 시간(P-time) 안에 확인할 수 있는 문제들의 집합이다

---

❓ Knapsack은 NP인가?

• 아니요 (Optimization ver 기준)

✔️ 설명

• 최대 이익이 500인 아이템 집합 A가 주어졌을 때,
  그것이 최대(maximum)인지 확인하려면 모든 조합(2ⁿ)을 비교해야 하므로,
  다항 시간 확인 불가능 → Optimization ver는 NP 아님.

• 하지만 Decision ver:

  “집합 A의 이익이 500을 넘는가?”는
  → O(n) 시간 안에 계산 가능 → NP 맞음
  (이건 단순히 합계를 계산하고 비교하면 되므로 빠름)

---

🔸 Polynomial-time Verification (다항 시간 검증)

• 문제 푸는 건 어렵지만, 해가 맞는지는 빠르게 검증 가능한 문제들이 있음
• 예: {i1, i3, i4}라는 집합이 주어지고 이게 500 넘냐? → 합만 보면 되므로 O(n) 검증 가능

---

🔸 Deterministic vs Nondeterministic

구분	설명
Deterministic	매 단계마다 한 가지 선택만 가능. 우리가 쓰는 일반 컴퓨터.
Nondeterministic	동시에 여러 선택을 시도하는 이론적 컴퓨터. 마치 "마법" 같은 가정.

---

🔸 Nondeterministic 알고리즘/머신 구성

1. Nondeterministic Guess (단계 1)

   • 문제 인스턴스가 주어지면,
     정답을 "순식간에" 추측해서 고른다 (정말 맞는 거라면).
   • 즉, 모든 가능성 중에서 정답을 딱 집어냄 (현실엔 없음, 이론용)

2. Deterministic Verification (단계 2)

   • 추측된 정답이 진짜 맞는지 다항 시간(P-time) 안에 검증

---

🔹 NP의 정의 요약

1. P-time Nondeterministic 알고리즘으로 풀 수 있는 문제들의 집합
2. 검증이 P-time 안에 가능한 문제들의 집합

→ 즉, "정답을 빠르게 확인할 수 있으면 NP"

---

🔸 P vs NP

• 💥 “P = NP인가?”는 컴퓨터 과학에서 가장 유명한 미해결 문제 중 하나

  • P ⊆ NP (맞음)
  • P = NP ❌ 아마 아님 (probably NO)

---

📌 주요 내용:

• 컴퓨터 과학(CS)에서 중요한 문제들은 거의 다 NP에 포함됨.
• 너무 많은 문제들이 P에 속함을 증명할 수 없음.
• ⏩ “NP-Complete 문제 중 하나라도 P에 포함된다면, 모든 NP-Complete 문제도 P에 포함된다.”

---

✅ NP-Complete 정의

def.1) 문제 B가 NP-Complete이 되려면:

1. B가 NP에 속하고
2. 모든 A ∈ NP에 대해 A ≤p B (다항 시간 변환 가능)

def.2) 문제 C가 NP-Complete이면:

1. C가 NP에 속하고
2. 어떤 NP-Complete 문제 B에 대해 B ≤p C

👉 즉, 다른 NP 문제로부터 다항 시간 내에 변환(transform) 가능하고, 그 자체도 NP에 속해야 함.

---

📜 Cook's Theorem (1971)

“만약 CNF 문제(CNF-SAT)가 P에 속한다면, P = NP이다.”

• 이 말은 CNF-SAT 문제가 최초로 NP-Complete임을 증명한 결과로 유명함.
• CNF-SAT: Conjunctive Normal Form Satisfiability (불 논리식의 만족 여부 판단 문제)

---

✅ CNF-SAT 설명

• CNF(합동 정규형): 여러 개의 OR 조건이 AND로 연결된 불 논리식 예:
  (x1 ∨ x2) ∧ (x2 ∨ ¬x3)

• 예시 문제:

  • x1 = T, x2 = F, x3 = F일 때 식이 참(True)이 되는지 판단.

• 이 문제는 Decision Problem (예/아니오로 답할 수 있음)

---

🧠 중요한 질문

❓ "CNF에서 변수 개수가 100만 개면 어떻게 푸나?"

답:

• BF(Brute Force),
• Greedy,
• Divide & Conquer,
• Branch & Bound 등의 다양한 설계 기법들을 사용하여 분석/설계.

---

🔸 핵심 주제:

"어려운 문제를 NP-Complete로 증명할 수 있다."
즉, 어떤 문제가 NP-Complete임을 보이기 위해 이미 알려진 NP-C 문제로부터 다항시간 변환(reduction)하면 됨.

---

🔹 1. 동기 (Motivation)

“주어진 어려운 문제를 NP-C로 증명할 수 있다.”

• ✔️ 예: SAT ⇒ (나의 문제)
  → SAT에서 나의 문제로 다항시간 변환이 가능하면, 나의 문제도 NP-C임.
• ✔️ NP-C 중 하나가 해결되면, 다른 NP-C들도 변환해서 해결 가능.

---

🔹 2. 정의: 다항시간 변환 (poly.time reducible)

A가 B로 다항 시간 안에 변환 가능하면
A =>p B 라고 씀.

• 즉, A 문제를 B 문제의 한 인스턴스로 바꿔서,
  B를 풀면 A도 푸는 것과 같도록 만드는 것.

✔️ Theorem:

• 만약 B가 P 클래스고 A =>p B면,
  → A도 P 클래스임.

---

🔹 3. Transformation 알고리즘

어떤 문제 A를 풀고 싶은데, B를 푸는 알고리즘이 있다면?

• A를 B로 변환하고 (x ⇒ y),
• B 알고리즘을 y에 적용한다.

✨ 중요 조건:

• 변환은 다항 시간 안에 수행 가능해야 함.
• 변환된 문제 y의 정답이 x의 정답과 동치(iff) 여야 함.

---

🔹 4. 예제: Hamiltonian Circuit Decision Problem (HC.DP)

• 이 문제도 NP-C임을 증명하려면:

  1. HC.DP가 NP에 속하고
  2. SAT.DP ⇒p HC.DP (SAT을 HC.DP로 변환)

이미 존재함! ✅

---

🔹 5. 퀴즈: TSP.DP (Traveling Salesman Problem, Decision Version)

• TSP.DP가 NP-Complete인지 보이기 위해:

  ➤ (조건)

  1. TSP.DP ∈ NP
  2. HC.DP ⇒p TSP.DP (HC.DP로부터 다항 시간 변환 가능)

위 조건이 만족되면 TSP.DP도 NP-Complete임.

---

🧠 결론 요약

내용	설명
NP-C 증명법	이미 NP-C인 문제로부터 변환 가능함을 보이면 됨
핵심 논리	"A ⇒p B" 이고 B가 P면, A도 P다
의미	많은 NP-C 문제들이 서로 변환 가능 → 하나만 P가 되어도 모두 해결 가능
예시	SAT ⇒p HC.DP ⇒p TSP.DP 등

---

다음은 이미지에 있는 NP-Complete 예시 및 변환 기법에 대한 전체 설명입니다:

---

🔶 1. HC.DP → TSP.DP 변환 예시

• HC.DP: Hamiltonian Circuit Decision Problem
• TSP.DP: Traveling Salesman Problem (결정형)

조건:

• HC.DP가 NP에 속하고
• SAT.DP가 HC.DP로 다항 시간 내 변환된다면
  → HC.DP는 NP-Complete!

변환 예시:

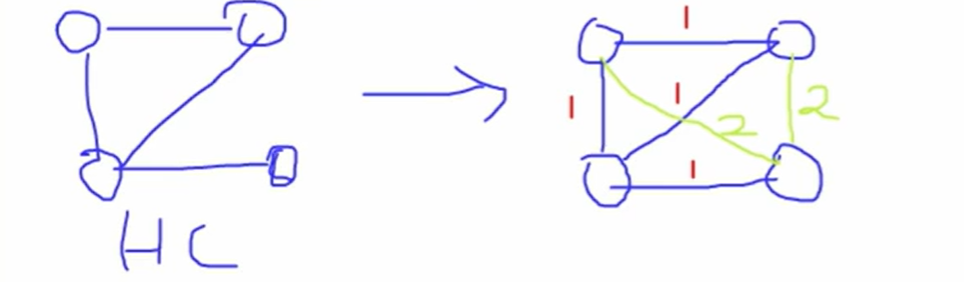
• HC의 edge면 cost=1
• edge가 없으면 cost=2
  → 이런 방식으로 TSP 그래프 구성하여 HC를 TSP로 바꿈

---

🔶 2. SAT → Clique 변환 예시

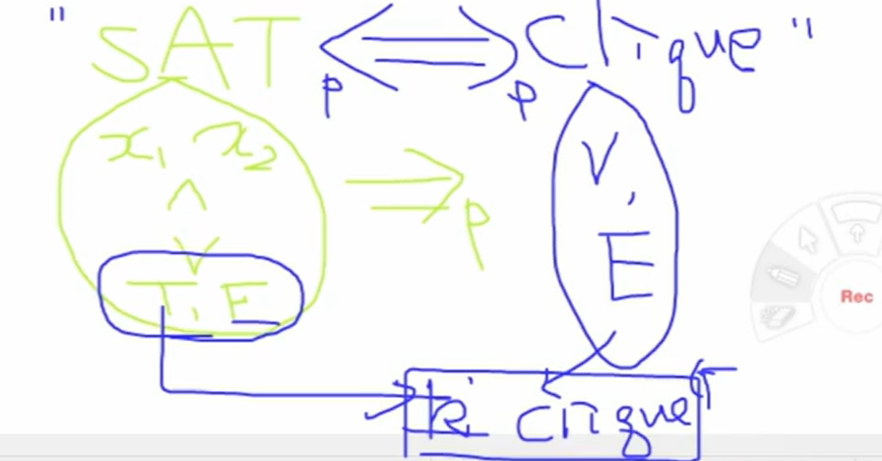
• SAT: CNF로 구성된 Boolean Satisfiability 문제
• Clique: 주어진 그래프에서 모든 노드가 서로 연결된 부분집합 찾기

방법:

• Boolean 식을 읽어서 Graph로 변환
• 변환 후, 해당 그래프에서 특정 크기의 Clique가 있는지 결정
• 변환은 Polynomial time 안에 수행됨

---

✅ 1. NP-Hard 문제란?

• 어떤 문제 A가 NP-Hard 라고 불리려면:

  • 모든 NP-Complete 문제 B에 대해
    B를 다항 시간 내 A로 변환(환원)할 수 있어야 함.
    (기호로는 B ⇒p A, 즉 다항시간 환원 가능)

즉, A가 풀리면 B도 풀릴 수 있으므로 A는 적어도 B만큼 어렵다는 의미입니다.

---

✅ 2. TSP는 NP-문제? NP-Complete?

● TSP (Traveling Salesman Problem)

• Optimization version (최적화 문제)
  : “모든 도시를 한 번씩 방문하고 다시 출발점으로 돌아오는 최단 경로는?”
  → ❌ NP가 아님, ❌ NP-Complete도 아님
  → ✅ NP-Hard 문제

• Decision version (결정 문제)
  : “100개 도시를 1시간 이내에 도는 경로가 있나?”
  → ✅ NP에 속함, ✅ NP-Complete임

📌 정리

• TSP-Optimization → NP-Hard
• TSP-Decision → NP-Complete

---

✅ 3. NP-Hard와 NP-Complete 차이

구분	NP-Complete	NP-Hard
NP 내부 포함?	✅ Yes	❌ No
해답 검증 쉬움?	✅ Yes (P-time 검증)	❌ 어렵거나 불가능
예시	SAT, Clique (결정문제)	TSP (최적화문제), Knapsack(최적화)

---

✅ 4. 예시로 본 TSP 검증 차이

🔹 TSP Decision:

given solution이 "100개 도시를 1시간 안에 도는 경로"인지?

• ✅ 가능: O(n) 시간에 체크 가능 (총 거리 계산하면 끝)

🔹 TSP Optimization:

이 경로가 최소 거리라고 어떻게 증명할 수 있나?

• ❌ 어려움: 모든 가능한 경로를 비교해야 해서 O(n!) 시간 소요

---

✅ 5. Knapsack 문제도 NP-Hard?

• Knapsack 문제는 최적화 문제(Optimization ver)가 기본이기 때문에:

  • ❌ NP가 아님
  • ✅ NP-Hard

• 해를 빠르게 검증하려면 O(2^n) 경우의 수 다 비교해야 함

---

✅ 결론: 왜 NP-Hard를 배우는가?

• 현실 세계의 많은 최적화 문제들이 NP-Hard
• 정확히 풀기 힘들어서 근사해법, 휴리스틱, 설계기법이 필요함
• 문제 분류(NP, NP-Complete, NP-Hard)를 통해 설계 방향을 정할 수 있음

---