Approximation Algorithms

✅ Approximation Algorithm 특징

1. 근사치 계산

• 최적이 아닌 "괜찮은" 해를 빠르게 찾기 위해 사용.
• 설계하기 쉬움. 보통 그리디(greedy) 기법 사용.

2. 근사 성능 평가 (얼마나 근접했는가?)

• a. 수학적 기준:

  • Bound Theorem 사용:

    • 예: approx ≤ optimal × 2
    • 더 작은 bound일수록 좋은 알고리즘

• b. 실험적 기준:

  • 정확도, 실제 데이터에서 얼마나 잘 작동하는지

3. 실행 시간 (얼마나 빠른가?)

• a. 수학적 시간 복잡도 → T(n) = polynomial
• b. 실험적 실행 시간 → 실제 걸리는 초 단위 시간

---

✅ 개발 접근법

• 대부분 Greedy 기반 Heuristic
• Classical Greedy vs Approximation Greedy는 다름
  (Approximation은 성능 한계를 명시적으로 분석)

---

✅ Boundness 개념

• 최적 해(optimal)를 계산하기 어려우므로,
  최적 해와 근사 해의 관계를 수학적으로 표현.

예시:

• 근사 해 ≤ 최적 해 × 2
• 근사 해 ≤ 최적 해 × 10 등

→ 이렇게 경계(bound)를 줄 수 있다면 이론적으로 훌륭함.

✅ Bound가 작을수록 더 좋은 알고리즘이다!

---

🔚 요약

항목	설명
목적	NP-Hard 문제의 대안적 해결
방법	빠른 알고리즘 (보통 Greedy) 사용
평가	얼마나 근접한가 (Bound), 얼마나 빠른가 (Time)
핵심 개념	Bound Theorem, Greedy, Heuristic

---

📌 핵심 주제:

MST(Minimum Spanning Tree)를 이용한 TSP 근사 알고리즘 (Approximation Algorithm)

---

✅ 아이디어 (상단 왼쪽)

• MST는 짧은 간선들만으로 연결된 구조 → 비용이 작음
• 사이클이 없음
• 하지만 모든 정점을 돌고 다시 시작점으로 돌아오는 루트 (TSP) 구성에 활용 가능

---

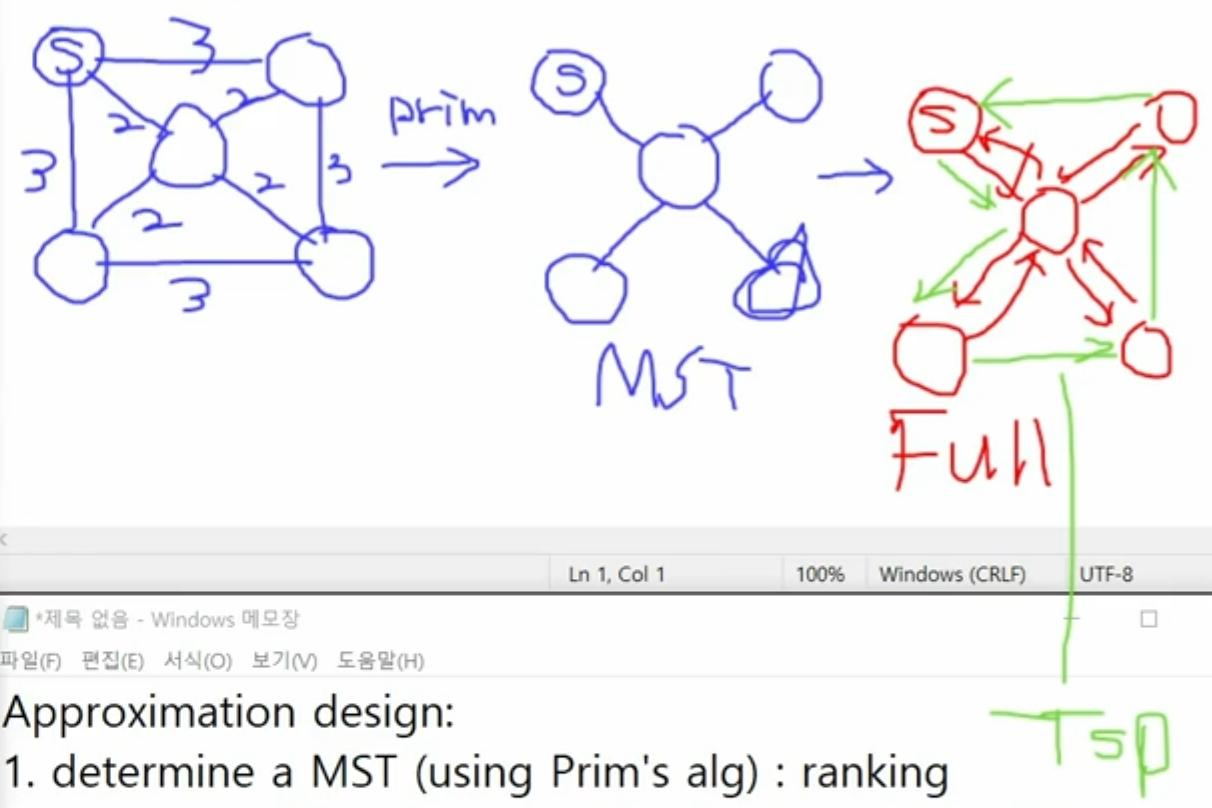
1. 왼쪽 그림: 원래 그래프
2. 가운데 그림: Prim 알고리즘으로 구한 MST
3. 오른쪽 그림: MST 기반으로 만든 TSP 경로 (모든 정점 방문 후 돌아옴)

---

✅ 설계 단계 (오른쪽 하단)

1. Prim 알고리즘으로 MST 구함
2. MST를 기반으로 preorder DFS 순회해서 path 생성

---

✅ 분석 내용

📍1. Time Complexity (시간 복잡도)

• MST 구성: O(n^2) (Prim’s 알고리즘 기준)
• 전체 알고리즘도 O(n^2) 다항 시간

📍2. Boundness (근사 해의 성능 보장)

• 실제 근사 해 p 와 최적 해 p* 관계:

즉, 근사 해는 최적 해의 2배를 넘지 않음 (이게 바로 bound theorem)

---

✅ 수식 요약 (왼쪽 하단)

• cost(MST.path) < cost(p*)
• cost(Full walk on MST) = 2 × cost(MST)
  → 즉, MST를 따라 왕복하면 2배 비용
• cost(p) < cost(Full walk) (삼각 부등식 이용)

---

📌 결론

• TSP는 NP-Hard라 최적 해 찾기 어려움
• MST 기반 근사 알고리즘을 사용하면
  다항 시간 안에 최적 해에 가까운 해(2배 이내)를 구할 수 있음

---

📌 문제 개요: Bin Packing Problem

• 입력: 크기가 $s_1, s_2, ..., s_n$ 인 n개의 아이템 (각 $0 < s_i \leq 1$)
• 목표: **최소 개수의 bin(용량 1인 통)**에 이 아이템들을 포장(packing)

즉, "적은 수의 bin으로 모든 아이템을 담는 방법은?"
이는 **최적화 문제 (Optimization Problem)**이며, NP-Hard 문제입니다.

---

✅ 실생활 응용 예시

• 이사짐, 여행 가방 포장
• 인테리어 배치 최적화
• 서버 로드 밸런싱, 자원 분배 등

---

🔧 해결 방법 방향성

Bin Packing은 NP-Hard라서 최적 해를 빠르게 찾기 어렵기 때문에:

💡 Approximation Algorithm (근사 알고리즘) 사용
→ 빠르게 실행되면서도, 최적 해에 가까운 해를 구하는 것이 목적

🎯 문제 목표

• Subset Sum Problem을 Bin Packing Problem으로 변환하고, Bin Packing이 NP-Hard임을 증명하기

• 즉, Subset Sum 인스턴스를 Bin Packing으로 바꿔서 해결 가능하게 만드는 것

• 이걸 통해:

  “Bin Packing 문제는 Subset Sum만큼 어렵다” = NP-Hard임을 보이는 것

---

📌 1. Subset Sum Problem 정의

• 입력:

  • 집합 $S = \{s_1, s_2, ..., s_n\}$
  • 목표 합 $T$

• 질문:

  집합 $S$에서 합이 정확히 $T$인 부분집합이 존재하는가?

---

📌 2. Bin Packing Problem 정의

• 입력:

  • 아이템 $s_1, ..., s_n$ 각각 크기 $0 < s_i \le 1$
  • 단위 용량의 bin들 (용량 = 1)

• 목표:

  최소 개수의 bin에 모든 아이템을 포장하라 (각 bin 합 ≤ 1)

---

📌 3. 환원 아이디어 (Subset Sum → Bin Packing)

✅ 변환 방법:

1. Subset Sum의 각 정수 $s_i$ 를 비율화:

   $s'_i = \frac{s_i}{T}$

   (즉, 전체를 T로 나눠서 0~1 사이로 만듦)

2. 그러면 이제 $s'_i$ 들로 이루어진 Bin Packing 문제가 생성됨.

3. 이제 질문을 바꿔서 이렇게 묻는다:

   s'_i 아이템들을 1개의 bin에 정확히 맞게 포장할 수 있는가?

   ⟶ 그 말은:

   합이 정확히 1인 부분집합이 존재하는가?
   ⟶ 원래 Subset Sum에서 $T$를 만드는 부분집합이 있는가?

---

📌 4. 결론: 문제 동등성

• Subset Sum에서 $\sum s_i = T$ 인 부분집합이 존재
  ⟺ Bin Packing에서 $\sum s'_i = 1$ 인 부분집합이 존재
  ⟶ 둘은 같은 문제, 표현만 바뀐 것

---

✅ 따라서:

• Subset Sum은 NP-complete
• Subset Sum ⟶ Bin Packing으로 다항시간에 변환 가능
• 그러므로 Bin Packing은 NP-Hard (최적화 문제)

---

📌 요약 정리

항목	설명
문제 이름	Bin Packing Problem
분류	NP-Hard
입력	크기 $s_i \in (0,1]$ 인 아이템 n개
목표	bin의 개수 최소화
적용	근사 알고리즘으로 빠르게 해를 구함

---

이 슬라이드는 **Bin Packing Problem (NP-Hard 문제)**에 대한 근사 알고리즘 (Approximation Algorithm) 설계 및 분석 내용을 담고 있습니다. 하나씩 설명해드릴게요:

---

✅ 문제 정의 (왼쪽 상단)

• Bin Packing Problem:

  • n개의 아이템 $\{s_1, s_2, ..., s_n\}$ 크기 $0 < s_i \le 1$
  • 단위 용량 1.0인 bin에 최소 개수로 포장하라
  • 이 문제는 NP-Hard

---

✅ 근사 알고리즘: NFF (Nonincreasing First-Fit)

오른쪽 상단 내용

1. 아이템을 내림차순으로 정렬:
   0.85, 0.5, 0.4, 0.4, 0.3, 0.2, 0.2, 0.1

2. 첫 번째 bin부터 가능한 곳에 채워 넣기 (First-Fit)

✍ 예시 결과:

• 0.85 + 0.1 → B1
• 0.5 + 0.4 → B2
• 0.2 + 0.3 → B3
• 0.4 → B3에 못 들어감 → B4
• 총 4개 bin 사용

---

✅ 최적해 비교

최적해는 3개 bin으로 포장 가능함을 보여주는 예시:

• B1: 0.85 + 0.1
• B2: 0.2 + 0.3 + 0.5
• B3: 0.2 + 0.4 + 0.4

---

⏱ 시간 복잡도:

• 정렬 + 삽입 = $O(n \log n)$

📏 품질 분석:

• Bound Theorem:

  • 근사 해의 bin 개수는 최적 bin 수의 1.5배 이하
  • $\text{approx bins} < \text{OPT} \times 1.5$

📌 보조정리 (lemma):

• 추가로 사용된 bin에 들어가는 item들은 크기가 1/3 이하인 것만 있음
  → 이는 분석에 사용됨 (품질 증명)

---

🔚 요약

항목	설명
문제	최소 bin 개수로 아이템 포장 (단위 용량 bin)
난이도	NP-Hard
방법	NFF (Nonincreasing First-Fit)
결과	빠르지만 최적은 아님 (정확도는 증명됨)
근사 해 품질	최적 bin 수의 1.5배 이하 (보장됨)

---