[번역] Fundamentals of Data Visualization - 9 Visualizing many distributions at once
Fundamentals of Data Visualization

9 Visualizing many distributions at once
이 글에서는 여러 분포를 동시에 시각화하는 방법에 대해 설명하고 있습니다. 예를 들어, 날씨 데이터를 고려해 볼 때, 우리는 특정 달마다 온도가 어떻게 변하는지를 시각화하고, 각 달에 관측된 온도 분포도 보여주고 싶을 수 있습니다. 이 경우, 12개의 온도 분포를 한 번에 보여줘야 하는데, 이는 각 달에 하나씩 할당됩니다. 기존에 논의된 시각화 기법들은 이러한 상황에 적합하지 않으며, 이럴 때는 상자 그림(boxplots), 바이올린 그림(violin plots), 그리고 리지라인 그림(ridgeline plots)이 유효한 방법이 됩니다.
9.1 Visualizing distributions along the vertical axis
가장 단순한 방법은 각 분포의 평균 또는 중앙값을 점으로 표시하고, 그 주위의 변화를 오차 막대로 나타내는 것입니다. 그러나 이 접근 방식에는 여러 문제가 있다고 언급하고 있습니다. 첫째, 하나의 점과 두 개의 오차 막대로 분포를 표현함으로써 많은 데이터를 잃게 됩니다. 둘째, 점이 무엇을 나타내는지 즉시 명확하지 않습니다. 셋째, 오차 막대가 무엇을 의미하는지 명확하지 않으며, 이는 독자가 혼동할 수 있는 부분입니다. 마지막으로, 오차 막대가 대칭적일 때 데이터가 왜곡될 수 있습니다. 이 문제점들로 인해 이 접근법은 부적절하다고 결론짓고 있습니다.
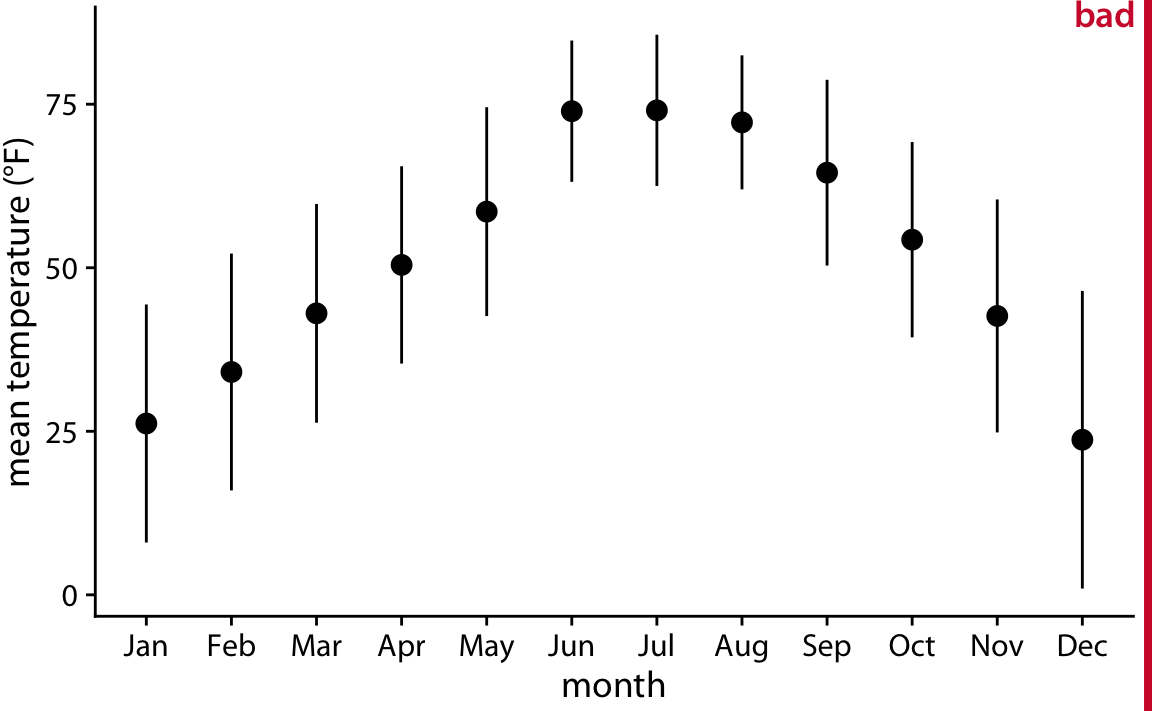
그림은 2016년 네브래스카주 링컨에서의 평균 일일 온도를 나타내며, 각 점은 해당 달의 평균 일일 온도를 나타내고, 오차 막대는 해당 달의 평균 일일 온도에서 두 배의 표준 편차를 나타냅니다. 그러나 이 그림은 "잘못된" 것으로 평가됩니다. 그 이유는 오차 막대가 추정치의 불확실성을 시각화하는 데 관례적으로 사용되지만, 여기서는 모집단의 변동성을 나타내기 때문입니다.
이러한 문제를 해결하기 위해 제안된 방법은 전통적이고 일반적으로 사용되는 상자 그림(boxplot)입니다. 상자 그림은 데이터를 사분위수로 나누어 이를 표준화된 방식으로 시각화합니다.
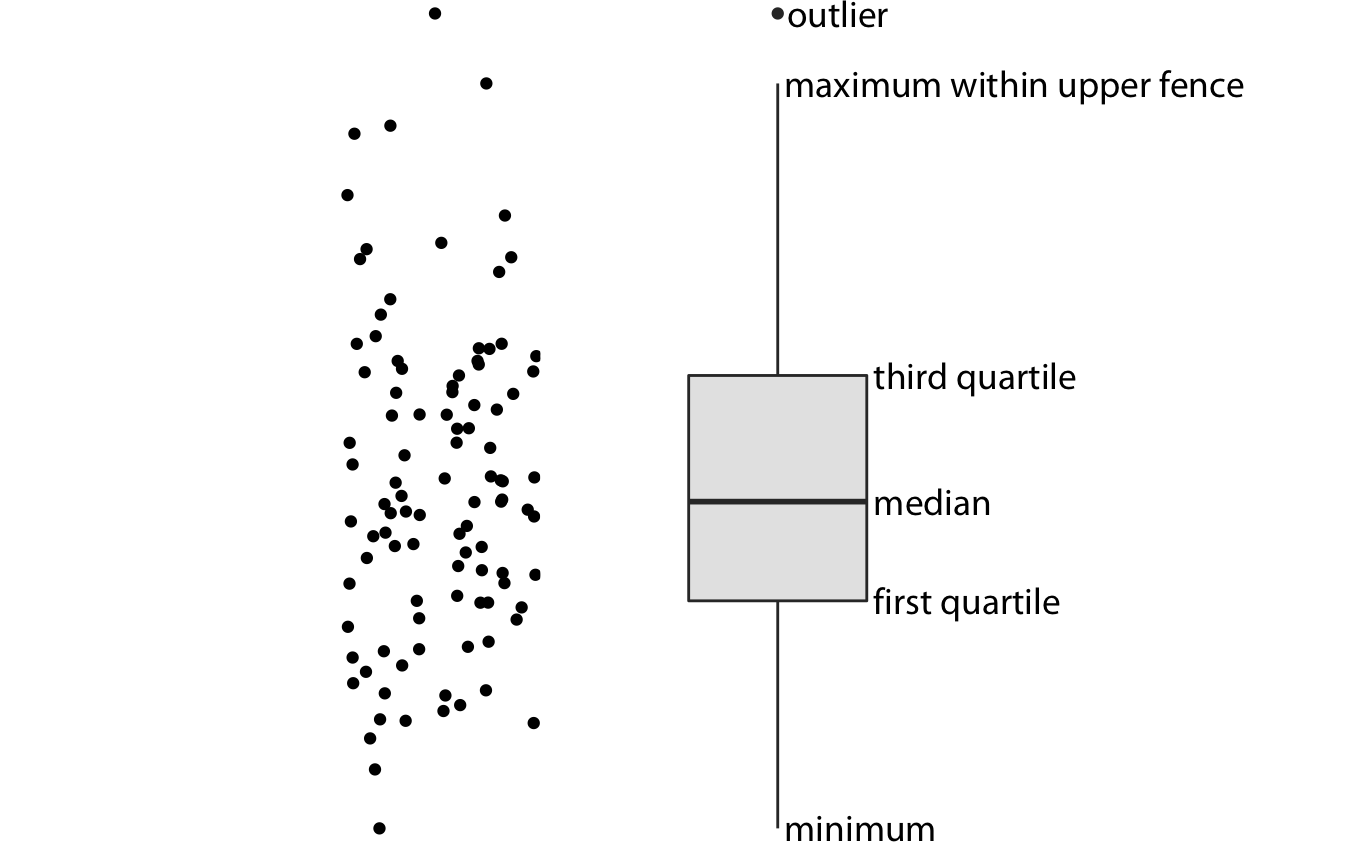
왼쪽에는 점 구름(cloud of points)이 표시되어 있고, 오른쪽에는 해당하는 상자 그림이 표시되어 있습니다. 상자 그림에서는 점의 y 값만 시각화됩니다. 상자 그림의 중앙에 있는 선은 중앙값(중위수)을 나타내며, 상자는 데이터의 중간 50%를 포함합니다. 상자 그림의 위쪽과 아래쪽의 '수염(whiskers)'은 데이터의 최대값과 최소값까지 또는 상자의 높이의 1.5배 내에 있는 최대값이나 최소값까지 확장됩니다. 이 중 짧은 수염이 선택됩니다. 상자의 높이의 1.5배 거리까지의 범위를 각각 상한선(upper fence)과 하한선(lower fence)이라고 부릅니다. 상한선이나 하한선 밖에 있는 개별 데이터 포인트는 이상치(outliers)라고 불리며, 보통 개별 점으로 표시됩니다.
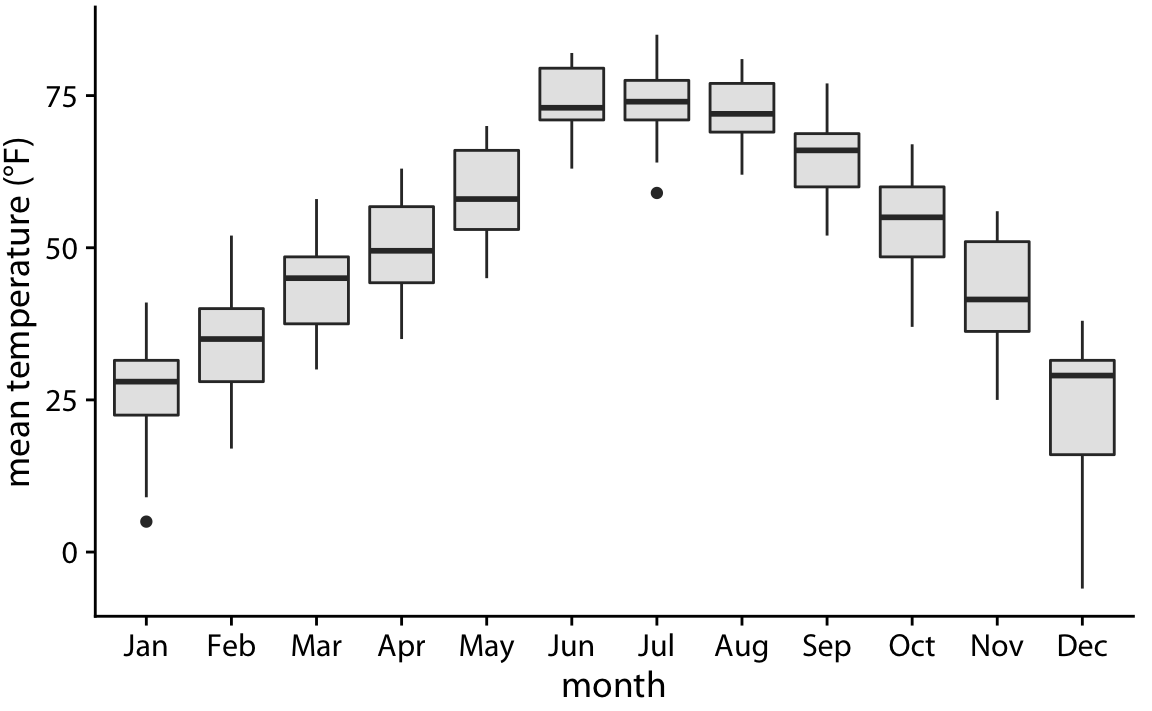
링컨의 온도 데이터를 상자 그림으로 표현하면 위와 같습니다. 이 그림에서는 12월의 온도가 매우 비대칭적으로 분포되어 있음을 확인할 수 있습니다(대부분의 날은 적당히 추우며, 일부 날은 매우 추움). 반면, 7월과 같은 다른 달에서는 온도 분포가 거의 비대칭적이지 않음을 알 수 있습니다.
최근에는 상자 그림이 바이올린 그림으로 대체되는 경우가 많습니다. 바이올린 그림은 7장에서 논의된 밀도 추정(density estimates)과 동일하지만, 90도 회전시켜 거울상으로 배치한 것입니다. 바이올린 그림은 상자 그림을 사용할 상황에서 언제든지 사용할 수 있으며, 데이터의 훨씬 더 세밀한 그림을 제공합니다. 특히, 바이올린 그림은 상자 그림이 정확하게 표현하지 못하는 이중 봉우리(bimodal) 데이터를 정확하게 나타낼 수 있습니다.
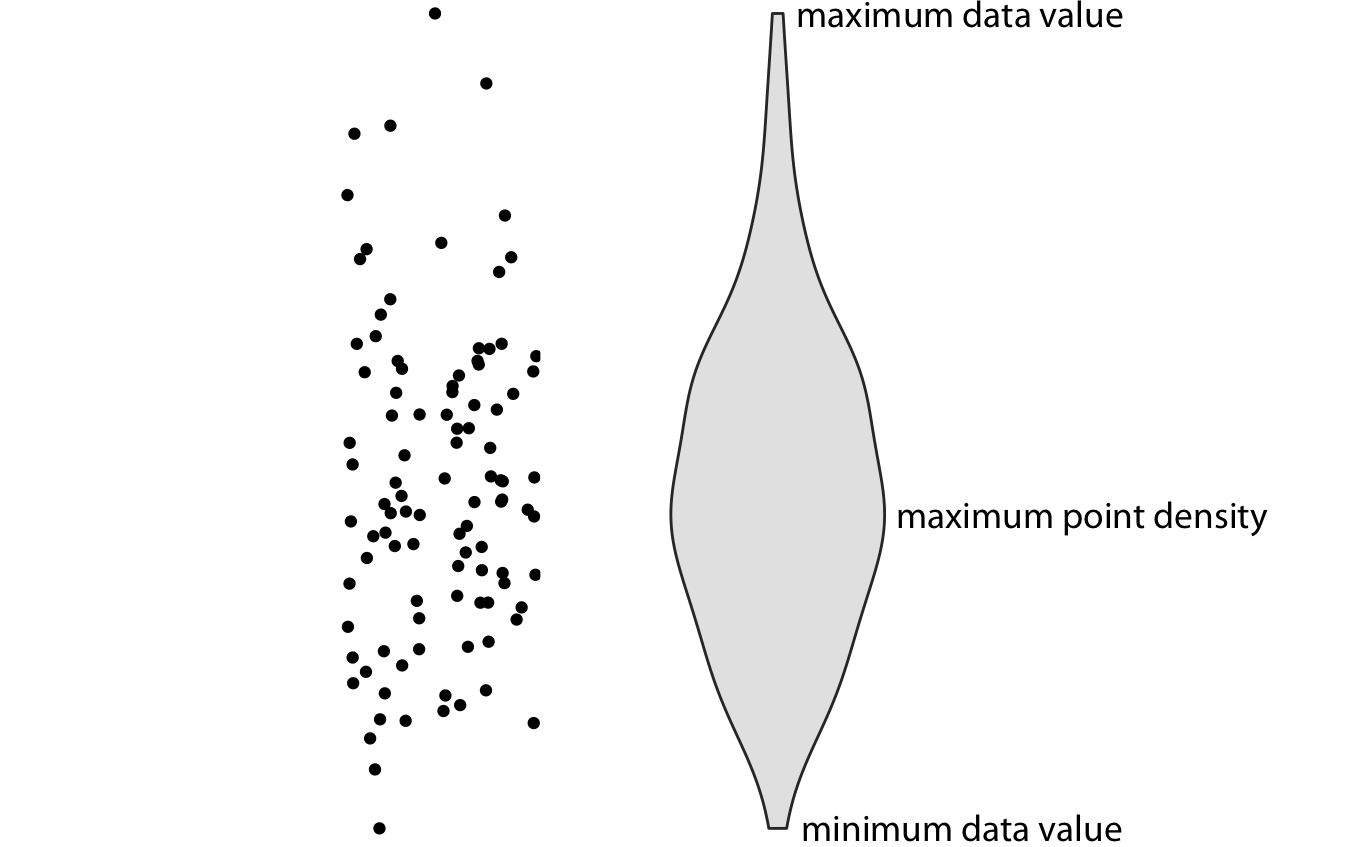
왼쪽에는 점 구름(cloud of points)이 표시되어 있고, 오른쪽에는 해당하는 바이올린 플롯이 표시되어 있습니다. 바이올린 플롯에서는 점의 y 값만 시각화됩니다. 특정 y 값에서 바이올린의 폭은 해당 y 값에서의 점 밀도를 나타냅니다. 기술적으로, 바이올린 플롯은 밀도 추정(density estimate)을 90도 회전시켜 거울상으로 만든 것입니다. 따라서 바이올린 플롯은 대칭적입니다. 바이올린은 각각 데이터의 최소값과 최대값에서 시작하고 끝납니다. 바이올린의 가장 두꺼운 부분은 데이터 세트에서 가장 높은 점 밀도를 나타냅니다.
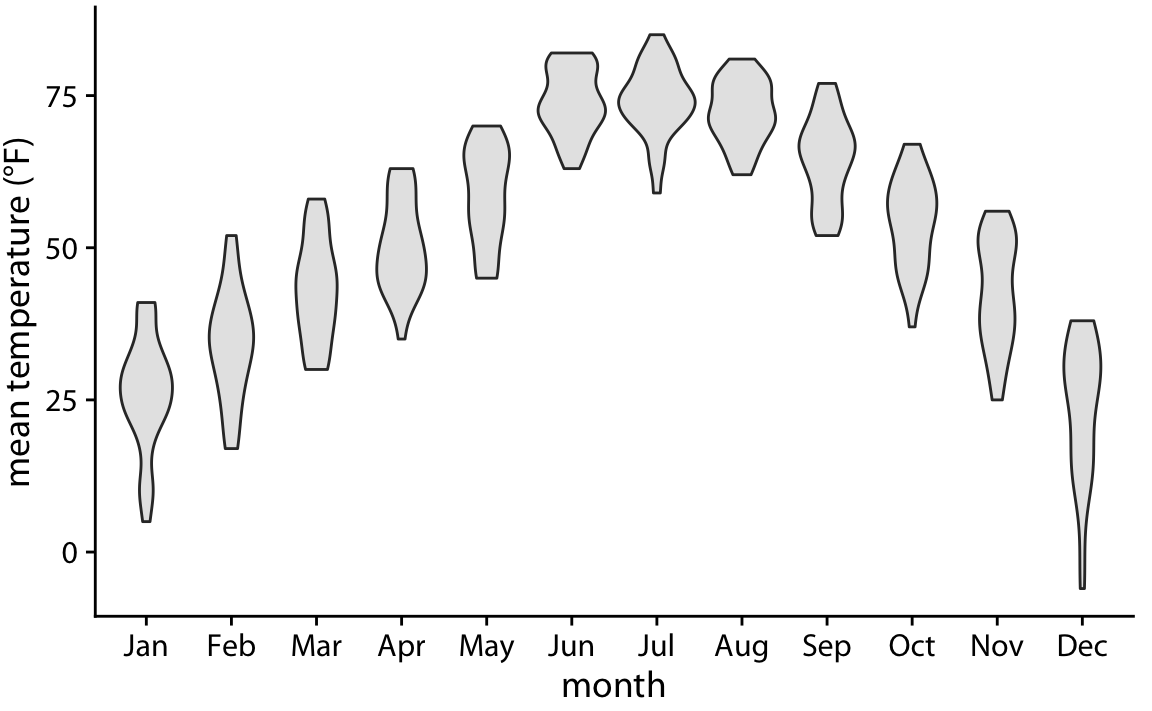
링컨의 온도 데이터를 바이올린 플롯으로 시각화하면 위와 같습니다. 이 그림에서 일부 달은 중간 정도의 이중 봉우리(bimodal) 데이터를 가지고 있음을 알 수 있습니다. 예를 들어, 11월은 두 개의 온도 클러스터를 가지고 있었는데, 하나는 약 50도 화씨 부근에, 다른 하나는 약 35도 화씨 부근에 위치해 있었습니다.
그러나 바이올린 플롯이 밀도 추정(density estimates)에 기반하기 때문에, 일부 단점이 있을 수 있습니다. 특히, 데이터가 실제로 존재하지 않는 곳에 데이터가 있는 것처럼 보이게 하거나, 데이터가 매우 희박한데도 불구하고 매우 밀집된 것처럼 보이게 할 수 있습니다.
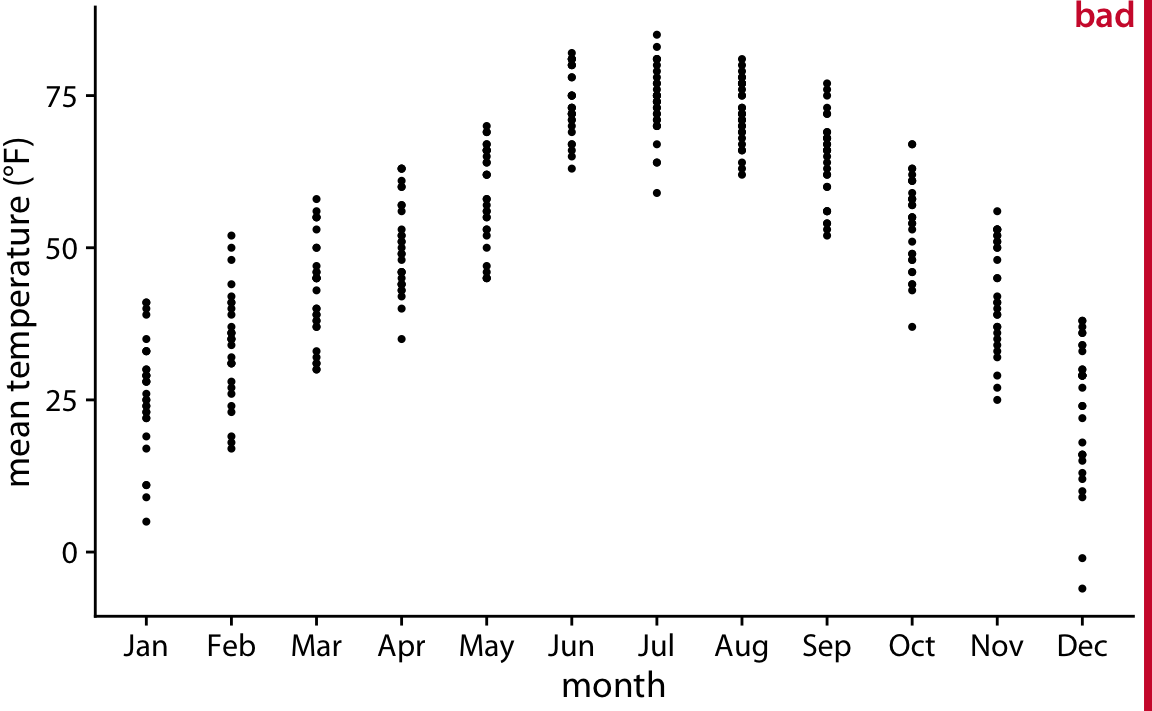
이러한 문제를 피하기 위해, 모든 개별 데이터 포인트를 직접 점으로 표시하는 방법을 사용할 수 있습니다. 아래의 그림은 이러한 방식을 사용한 시각화로, 이를 스트립 차트(strip chart)라고 부릅니다. 스트립 차트는 기본적으로 괜찮지만, 너무 많은 포인트가 서로 겹쳐서 표시되지 않도록 주의해야 합니다.
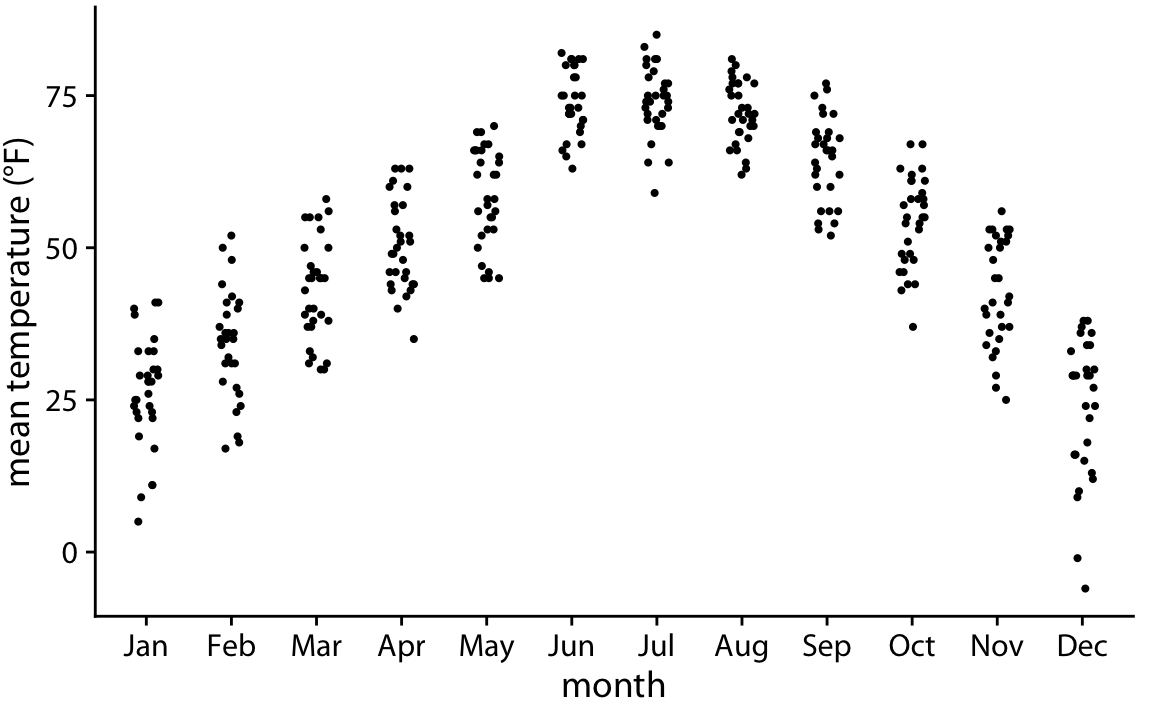
과도한 겹침(overplotting)을 방지하는 간단한 방법은 x축을 따라 포인트를 약간 퍼뜨리는 것입니다. 이를 위해 x축 차원에 약간의 랜덤 노이즈를 추가하는 기법을 사용할 수 있으며, 이를 jittering이라고 부릅니다.
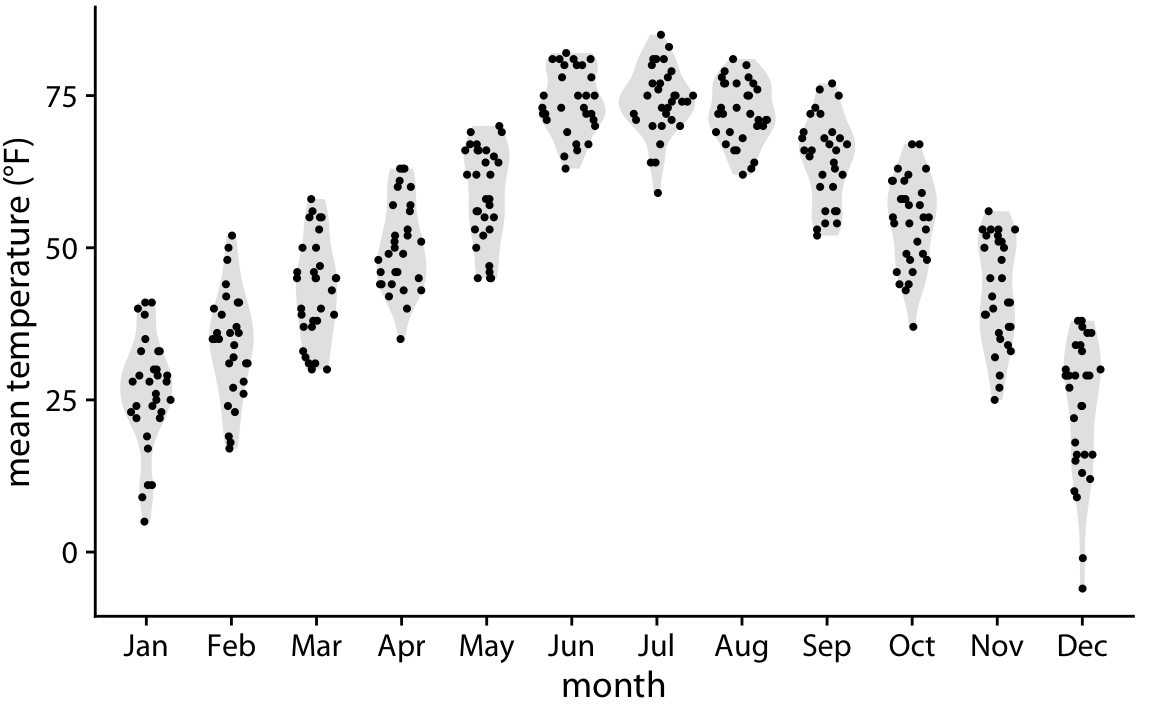
마지막으로, 두 가지 방법의 장점을 결합하는 방법으로 시나 플롯(sina plot)을 소개하고 있습니다. 시나 플롯은 특정 y 좌표에서 점의 밀도에 비례하여 점을 퍼뜨리는 방식으로, 바이올린 플롯과 지터링된 점의 하이브리드 형태로 생각할 수 있습니다. 시나 플롯은 각 개별 점을 보여주면서도 분포를 시각화할 수 있습니다.
9.2 Visualizing distributions along the horizontal axis
7장에서 히스토그램과 밀도 플롯을 사용하여 분포를 수평 축에 시각화했습니다. 여기서는 분포 플롯을 수직 방향으로 계단식으로 배치하여 확장하는 방법을 설명합니다. 이러한 시각화는 리지라인 플롯(ridgeline plot)이라고 하며, 산등성이처럼 보이는 것이 특징입니다. 리지라인 플롯은 특히 시간에 따른 분포의 경향을 보여줄 때 효과적입니다.
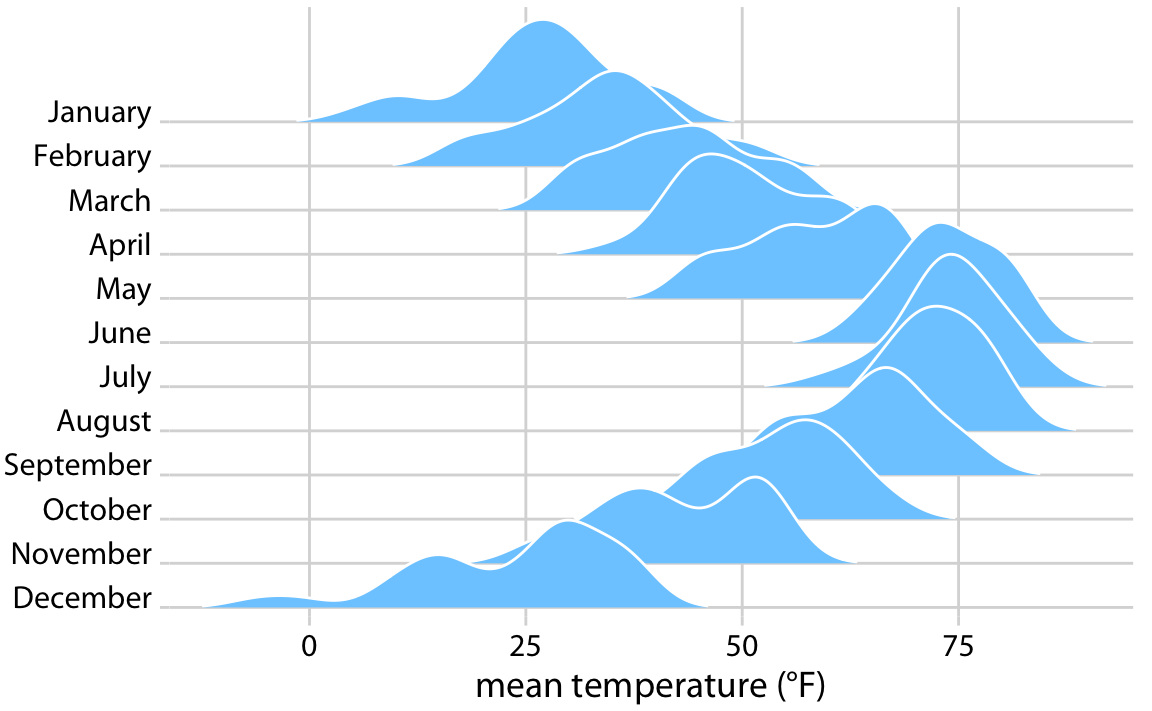
2016년 네브래스카주 링컨에서의 온도를 리지라인 플롯으로 시각화한 것입니다. 이 플롯에서는 각 달마다 일일 평균 온도의 분포를 화씨 단위로 보여줍니다. 리지라인 플롯에서는 x축이 반응 변수(온도)를, y축이 그룹핑 변수(달)를 나타내며, 밀도 추정치는 별도의 축 없이 그룹핑 변수와 함께 표시됩니다. 이는 바이올린 플롯과 동일한 방식으로, 특정 밀도 값을 보여주는 것이 아니라 그룹 간 밀도 모양과 상대적 높이를 쉽게 비교할 수 있도록 하는 것이 목적입니다.
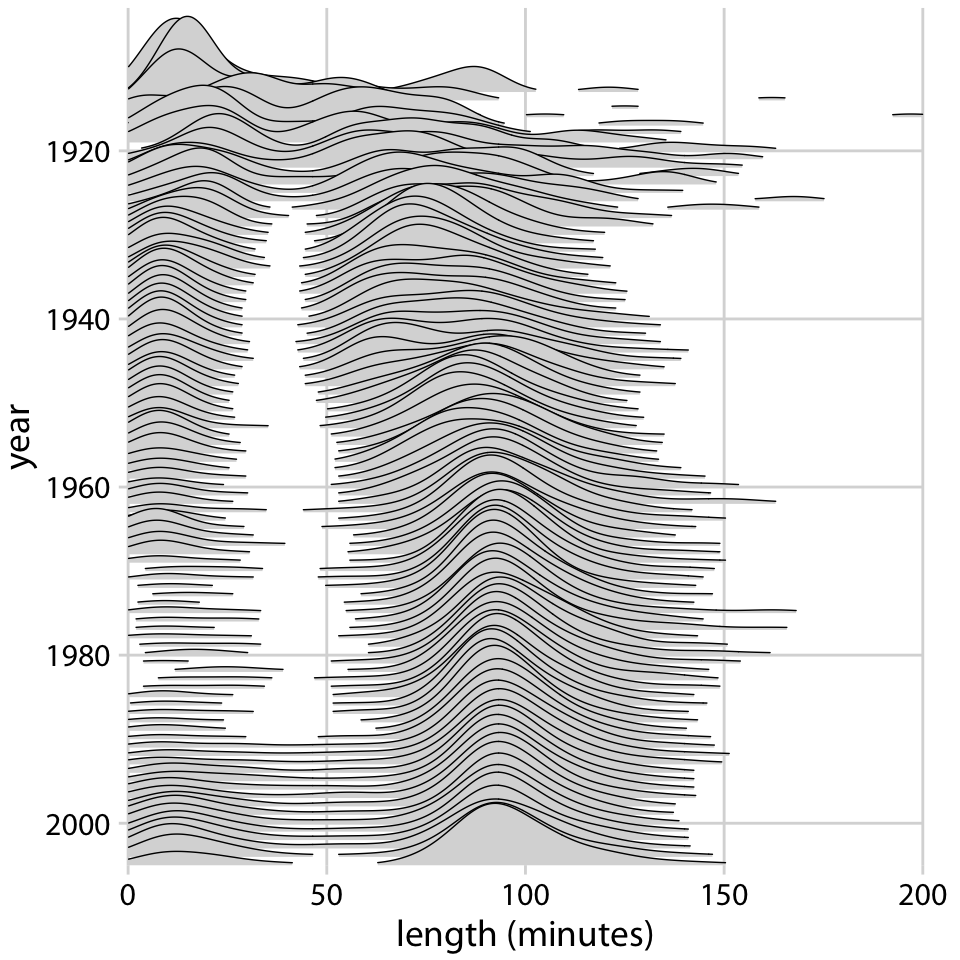
1913년부터 2005년까지 영화 길이의 분포를 리지라인 플롯으로 시각화한 예시가 제시됩니다. 이 그림은 거의 100개의 개별 분포를 포함하고 있지만, 여전히 읽기 쉽습니다. 이 그림을 통해 1920년대에는 영화 길이가 다양했지만, 약 1960년 이후로 영화 길이가 약 90분으로 표준화되었음을 알 수 있습니다.
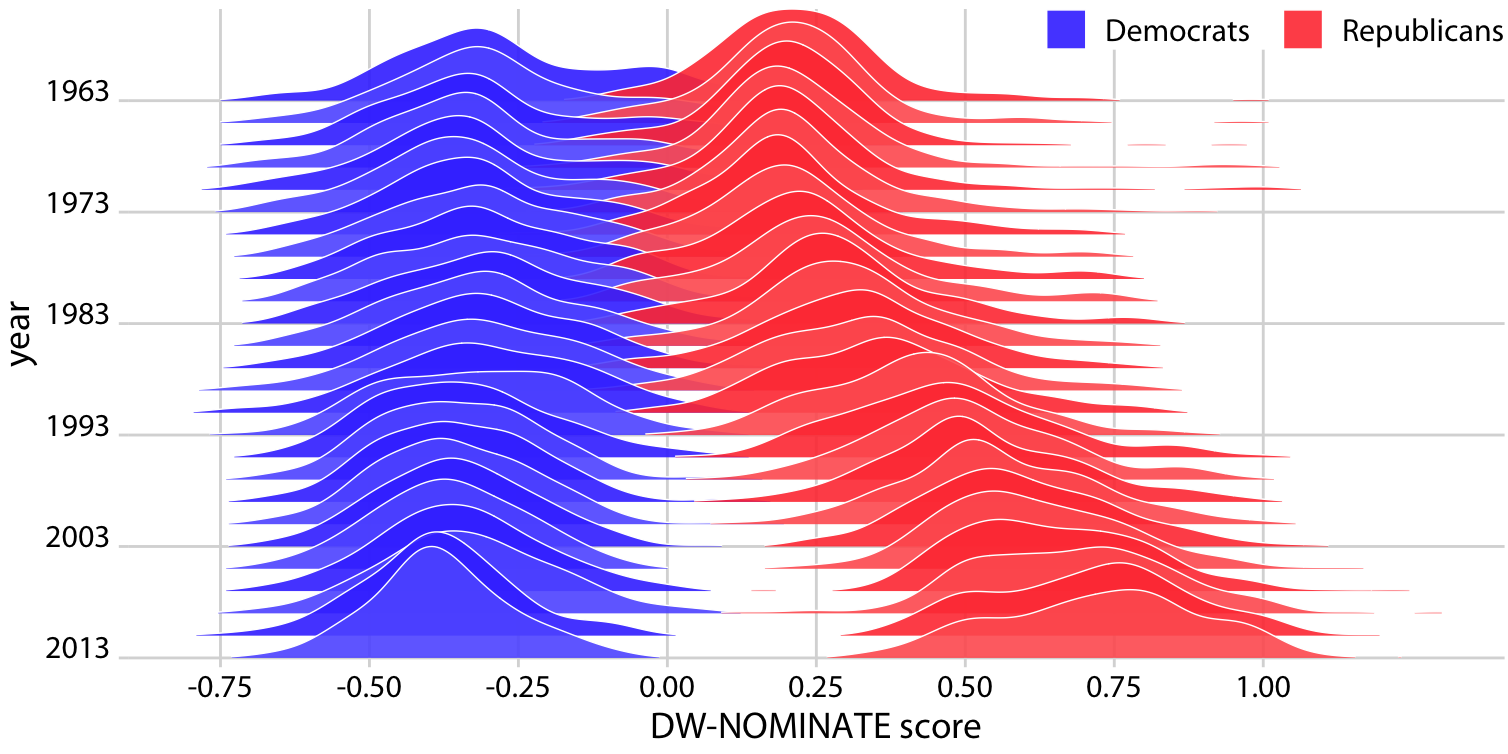
리지라인 플롯은 또한 두 가지 시간에 따른 추세를 비교할 때도 잘 작동합니다. 이는 두 정당의 투표 패턴을 분석할 때와 같은 시나리오에서 자주 발생합니다. 이러한 비교를 위해, 분포를 시간에 따라 수직으로 계단식으로 배치하고, 각 시간점에서 두 정당을 나타내는 두 개의 서로 다른 색상의 분포를 그릴 수 있습니다
