[번역] Fundamentals of Data Visualization - 12 Visualizing associations among two or more quantitative variables

12 Visualizing associations among two or more quantitative variables

많은 데이터셋이 두 개 이상의 양적 변수를 포함하고 있으며, 이러한 변수들이 서로 어떻게 관련되어 있는지를 알고 싶어 할 때가 있습니다. 예를 들어, 동물의 키, 몸무게, 길이, 일일 에너지 소모량과 같은 양적 측정값이 포함된 데이터셋이 있을 수 있습니다. 두 변수 간의 관계를 시각화하려면, 보통 산점도를 사용합니다. 그러나 두 개 이상의 변수를 동시에 나타내고 싶다면, 버블 차트, 산점도 행렬, 또는 상관 행렬과 같은 방법을 사용할 수 있습니다. 매우 고차원적인 데이터셋의 경우, 주성분 분석과 같은 차원 축소 기법을 사용하는 것이 유용할 수 있습니다.

12.1 Scatter plots

123마리의 blue jay 새에 대한 측정값이 포함된 데이터셋을 사용하여 기본적인 산점도와 그 변형을 시연합니다. 이 데이터셋에는 머리 길이(부리 끝에서 머리 뒤쪽까지 측정), 두개골 크기(머리 길이에서 부리 길이를 뺀 값), 몸무게와 같은 정보가 포함되어 있습니다. 이러한 변수들 간에는 관계가 있을 것으로 예상됩니다. 예를 들어, 부리가 더 긴 새는 더 큰 두개골을 가질 것으로 예상되며, 몸무게가 더 큰 새는 몸무게가 더 작은 새보다 더 큰 부리와 두개골을 가질 것으로 예상됩니다.

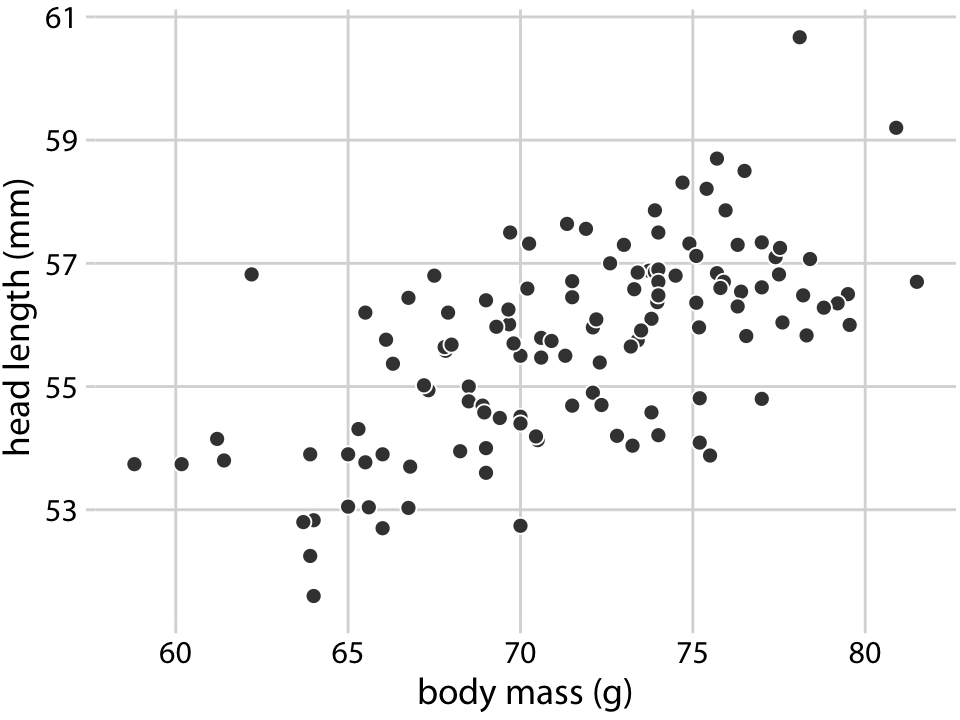
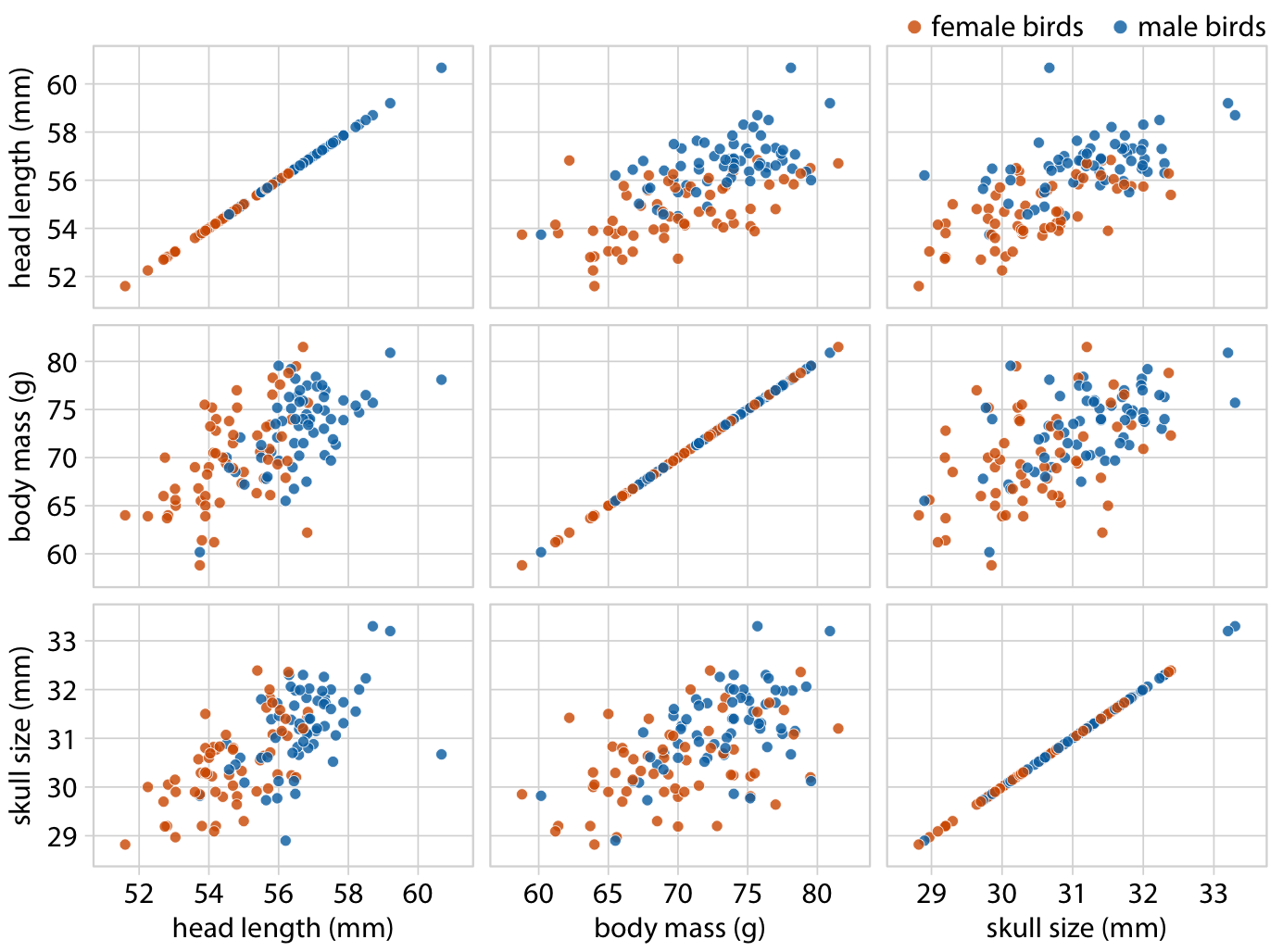
이러한 관계를 탐구하기 위해, 머리 길이와 몸무게 간의 관계를 나타내는 산점도를 그립니다. 이 그림에서 머리 길이는 y축에, 몸무게는 x축에 표시되며, 각 새는 하나의 점으로 표현됩니다. 점들은 분산된 구름 형태를 이루고 있지만, 몸무게가 더 큰 새들이 더 긴 머리를 가지는 경향이 있다는 추세가 분명히 보입니다. 가장 긴 머리를 가진 새는 관찰된 최대 몸무게에 가깝게 위치하며, 가장 짧은 머리를 가진 새는 최소 몸무게에 가깝게 위치합니다.

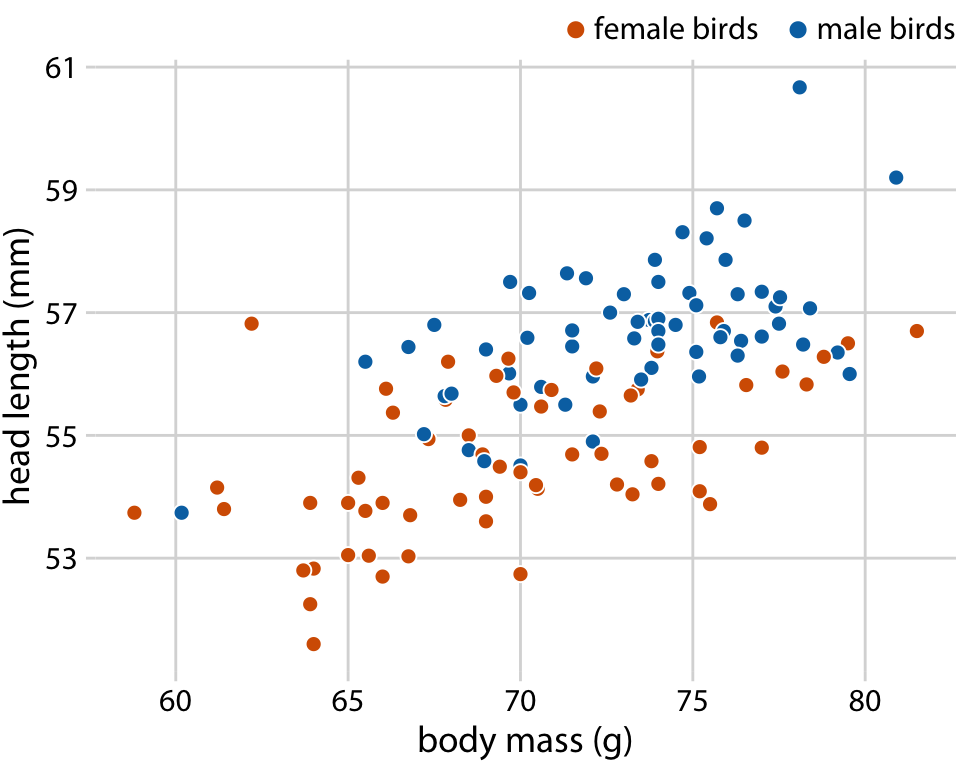
머리 길이와 몸무게 간의 관계가 성별에 따라 어떻게 달라지는지 확인해 보고자 하는 점을 다룹니다. 이를 위해 산점도의 점들을 새의 성별에 따라 색으로 구분합니다. 이 그림은 머리 길이와 몸무게 간의 전반적인 경향이 부분적으로 새의 성별에 의해 영향을 받는다는 사실을 보여줍니다. 동일한 몸무게에서 암컷은 수컷보다 머리가 더 짧은 경향이 있으며, 동시에 암컷이 평균적으로 수컷보다 더 가볍다는 점도 드러납니다.

머리 길이가 부리 끝에서 머리 뒤쪽까지의 거리로 정의되기 때문에, 머리 길이가 길다는 것은 부리가 더 길거나 두개골이 더 크다는 것을 의미할 수 있음을 언급합니다. 부리 길이와 두개골 크기를 구분하기 위해, 데이터셋의 또 다른 변수인 두개골 크기를 살펴봅니다.
이미 x축 위치에 몸무게를, y축 위치에 머리 길이를, 점의 색에 새의 성별을 매핑했기 때문에, 두개골 크기를 매핑할 또 다른 시각적 요소가 필요합니다. 이 경우 점의 크기를 사용하여 이를 표현할 수 있으며, 이렇게 하면 버블 차트라고 불리는 시각화가 됩니다.

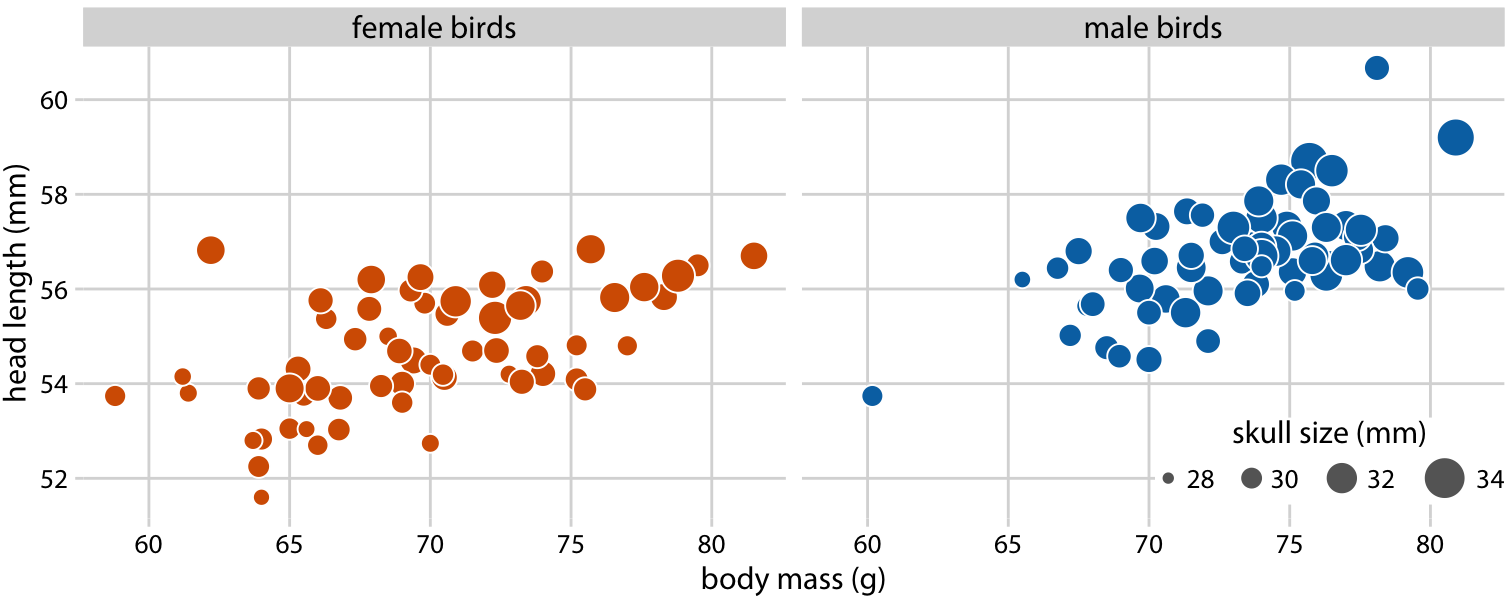
일반적으로 머리 길이와 두개골 크기는 상관관계가 있지만, 일부 새들은 두개골 크기에 비해 부리가 유난히 길거나 짧습니다.

버블 차트는 양적 변수를 서로 다른 유형의 척도(위치와 크기)로 나타낸다는 단점이 있습니다. 이는 변수들 간의 연관성 강도를 시각적으로 파악하기 어렵게 만듭니다. 또한, 크기로 인코딩된 데이터 값의 차이는 위치로 인코딩된 차이보다 인식하기 어렵습니다. 버블의 크기가 전체 그림에 비해 상대적으로 작아야 하기 때문에, 가장 큰 버블과 가장 작은 버블 간의 크기 차이는 작을 수밖에 없습니다. 결과적으로, 데이터 값의 작은 차이는 매우 작은 크기 차이로 나타나 거의 알아보기 어려울 수 있습니다. 두개골 크기(약 28mm에서 34mm)의 차이를 시각적으로 증폭시켜 나타냈지만, 두개골 크기와 몸무게 또는 머리 길이 간의 관계를 파악하기 어려운 경우도 있습니다.

버블 차트에 대한 대안으로, 모든 변수 간의 산점도를 개별적으로 보여주는 '전체 대 전체' 행렬이 더 나을 수 있습니다. 점의 크기보다 위치를 판단하는 것이 더 쉽기 때문에, 두개골 크기와 다른 두 변수(머리 길이와 몸무게) 간의 상관관계를 쌍별 산점도에서 더 쉽게 파악할 수 있습니다.

12.2 Correlograms

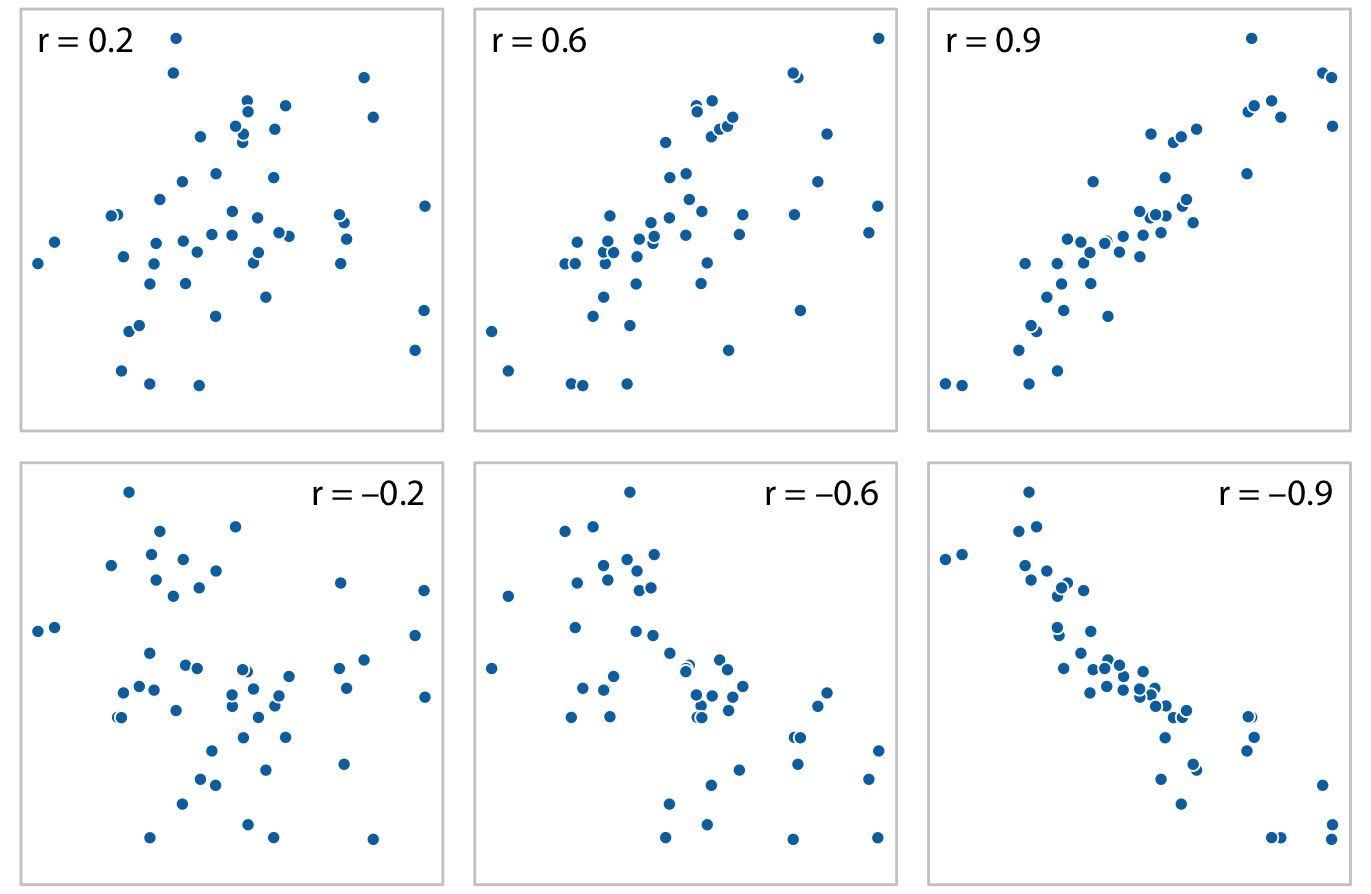
세 개에서 네 개 이상의 양적 변수가 있을 때, 모든 변수 간의 산점도 행렬은 빠르게 복잡해질 수 있음을 지적합니다. 이런 경우, 원시 데이터를 시각화하는 대신 변수 쌍 간의 연관성 정도를 정량화하고 이를 시각화하는 것이 더 유용할 수 있습니다. 일반적인 방법 중 하나는 상관계수를 계산하는 것입니다. 상관계수 r은 -1에서 1 사이의 값으로, 두 변수 간의 공분산 정도를 측정합니다. r=0은 두 변수 간에 전혀 연관성이 없음을 의미하며, r=1 또는 r=−1은 완벽한 연관성을 나타냅니다. 상관계수의 부호는 변수들이 서로 양의 상관관계(한 변수의 값이 커질수록 다른 변수의 값도 커짐) 또는 음의 상관관계(한 변수의 값이 커질수록 다른 변수의 값이 작아짐)에 있는지를 나타냅니다.

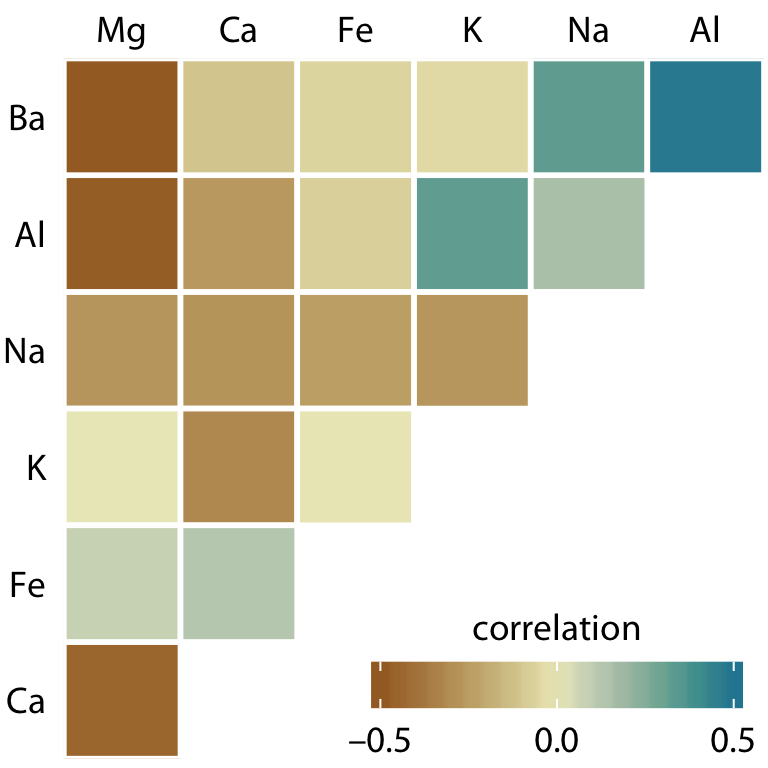
21개의 상관관계를 한 번에 색상 타일의 행렬로 표시할 수 있으며, 각 타일은 하나의 상관계수를 나타냅니다. 이 상관행렬은 데이터를 빠르게 파악할 수 있게 해주며, 예를 들어 마그네슘이 거의 모든 다른 산화물과 음의 상관관계를 가지며, 알루미늄과 바륨이 강한 양의 상관관계를 가진다는 점을 쉽게 알 수 있습니다.

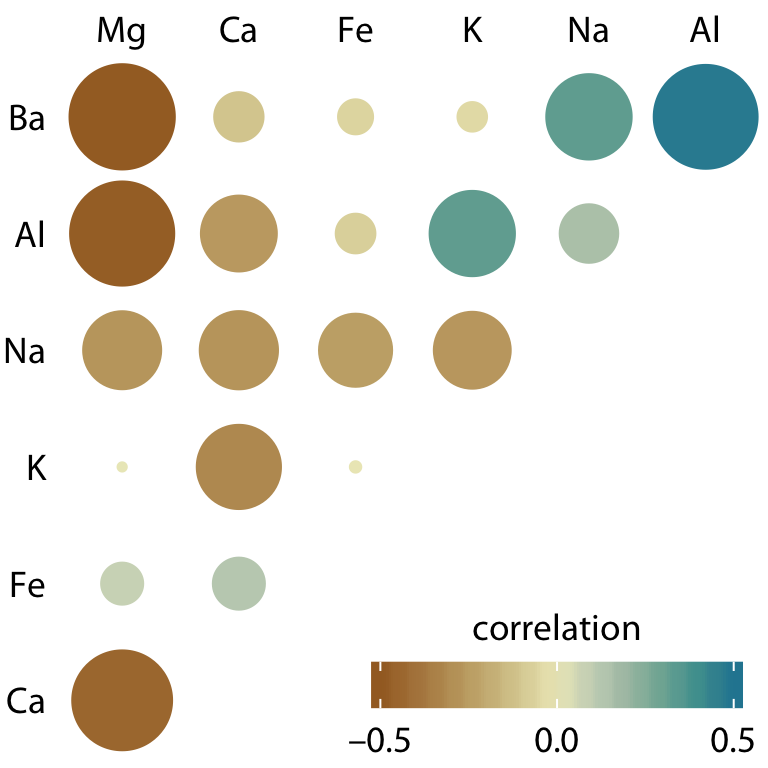
상관행렬에서 나타나는 약점 중 하나는 상관계수가 절대값 기준으로 0에 가까운 낮은 상관관계가 시각적으로 충분히 억제되지 않는다는 점입니다.이러한 제한점을 극복하기 위해, 상관관계를 색상 원으로 표시하고, 원의 크기를 상관계수의 절대값에 따라 조정할 수 있습니다. 이렇게 하면 낮은 상관관계는 시각적으로 억제되고, 높은 상관관계는 더욱 도드라지게 보일 수 있습니다.

12.3 Dimension reduction

상관행렬은 데이터에서 중요한 패턴을 보여주지만, 동시에 기초적인 데이터 포인트를 숨겨버릴 수 있어 잘못된 결론을 내리게 할 수 있습니다. 따라서, 계산된 추상적이고 파생된 양보다는 가능한 한 원시 데이터를 시각화하는 것이 항상 더 좋습니다. 다행히도, 중요한 패턴을 보여주면서 원시 데이터를 함께 보여줄 수 있는 중간 방법을 종종 찾을 수 있는데, 그것이 바로 차원 축소 기법을 적용하는 것입니다.

차원 축소에는 여러 가지 기법이 있으며, 여기서는 가장 널리 사용되는 기법 중 하나인 주성분 분석(PCA, Principal Components Analysis)에 대해 설명합니다. PCA는 데이터를 표준화하여 평균이 0이고 분산이 1이 되도록 한 원래 변수들을 선형 결합하여 새로운 변수 집합(주성분, PCs)을 도입합니다. 이 주성분들은 서로 상관관계가 없도록 선택되며, 첫 번째 주성분은 데이터의 변동성을 최대한 많이 포착하고, 이후의 주성분들은 점차적으로 적은 변동성을 포착하도록 정렬됩니다. 보통 데이터의 주요 특징들은 처음 두세 개의 주성분에서 확인할 수 있습니다.

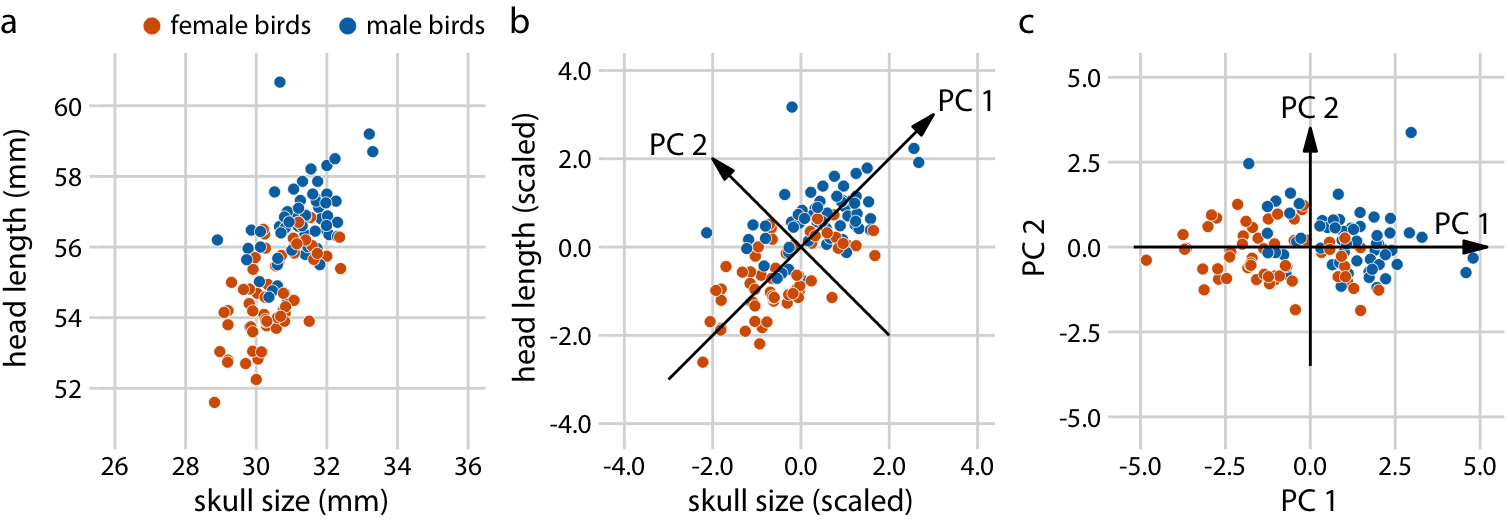
(a) 패널에서는 원본 데이터가 표시되어 있습니다. 여기서 사용된 데이터는 파랑어치(blue jay) 데이터셋의 머리 길이와 두개골 크기 측정값이며, 새의 성별은 색상으로 구분됩니다. 그러나 이 성별 구분은 PCA 분석에 영향을 미치지 않습니다. (b) 패널에서는 PCA의 첫 번째 단계로 원본 데이터 값을 평균이 0이고 분산이 1이 되도록 스케일링합니다. 그런 다음, 데이터의 최대 변동 방향을 따라 새로운 변수(주성분, PCs)를 정의합니다. (c) 마지막으로, 데이터를 새로운 좌표계로 투영합니다. 수학적으로 이 투영은 원점 주위에서 데이터 포인트를 회전시키는 것과 동일합니다. 여기서 보여준 2차원 예시에서는 데이터 포인트가 시계 방향으로 45도 회전합니다.

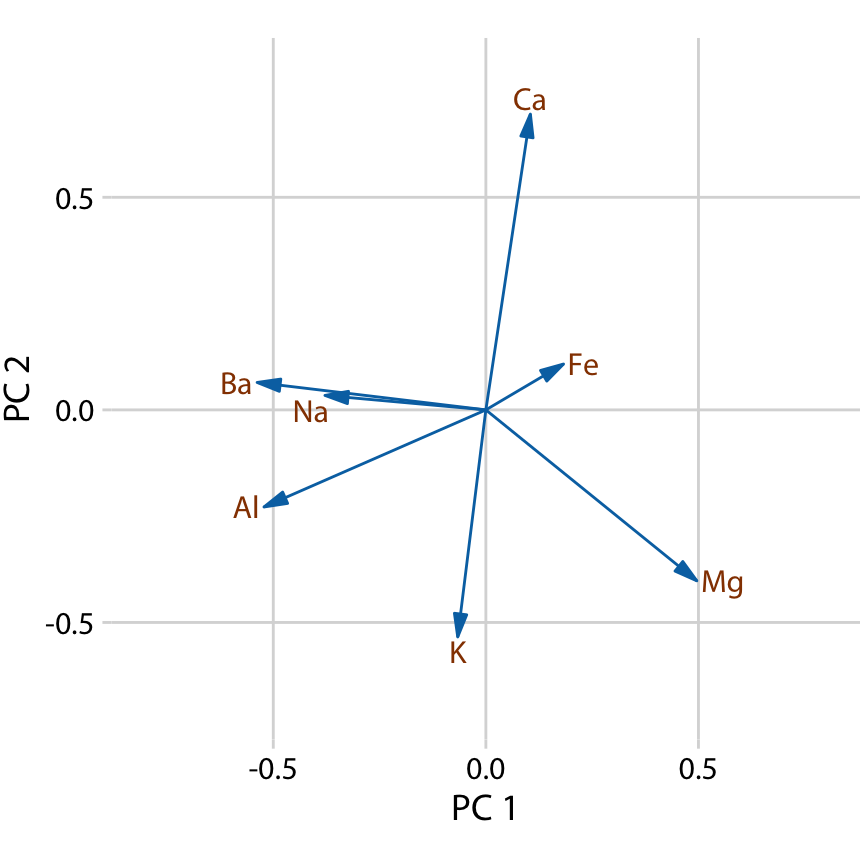
여기서는 첫 번째 두 개의 주성분, PC 1과 PC 2만 고려합니다. 주성분들은 원래 변수들의 선형 결합(표준화 이후)으로 구성되므로, 원래 변수들을 화살표로 표시하여 이들이 주성분에 어느 정도 기여하는지 나타낼 수 있습니다. 여기서 바륨(Ba)과 나트륨(Na)은 주로 PC 1에 기여하고 PC 2에는 기여하지 않으며, 칼슘(Ca)과 칼륨(K)은 주로 PC 2에 기여하고 PC 1에는 기여하지 않는 것을 볼 수 있습니다. 나머지 변수들은 두 주성분에 다양한 정도로 기여합니다(그림 12.9).

12.4 Paired data

짝지어진 데이터에서는 한 쌍에 속하는 두 측정값이 다른 쌍의 측정값보다 더 유사할 것이라고 합리적으로 가정할 수 있습니다. 예를 들어, 쌍둥이의 키는 대체로 비슷하지만, 다른 쌍둥이들과는 다를 것입니다. 따라서, 짝지어진 데이터를 시각화할 때는 두 측정값 간의 차이를 강조하는 시각화 방법을 선택해야 합니다.

이 경우 좋은 선택은 대각선(x = y)을 표시한 단순 산점도입니다. 이 플롯에서, 각 쌍의 두 측정값 간의 차이가 오직 무작위 노이즈로만 설명될 수 있다면, 샘플의 모든 점들이 이 대각선 주위에 대칭적으로 흩어지게 됩니다. 반면, 짝지어진 측정값 간의 체계적인 차이가 있다면, 데이터 포인트들은 대각선에 대해 위아래로 체계적으로 이동하는 것이 보입니다.

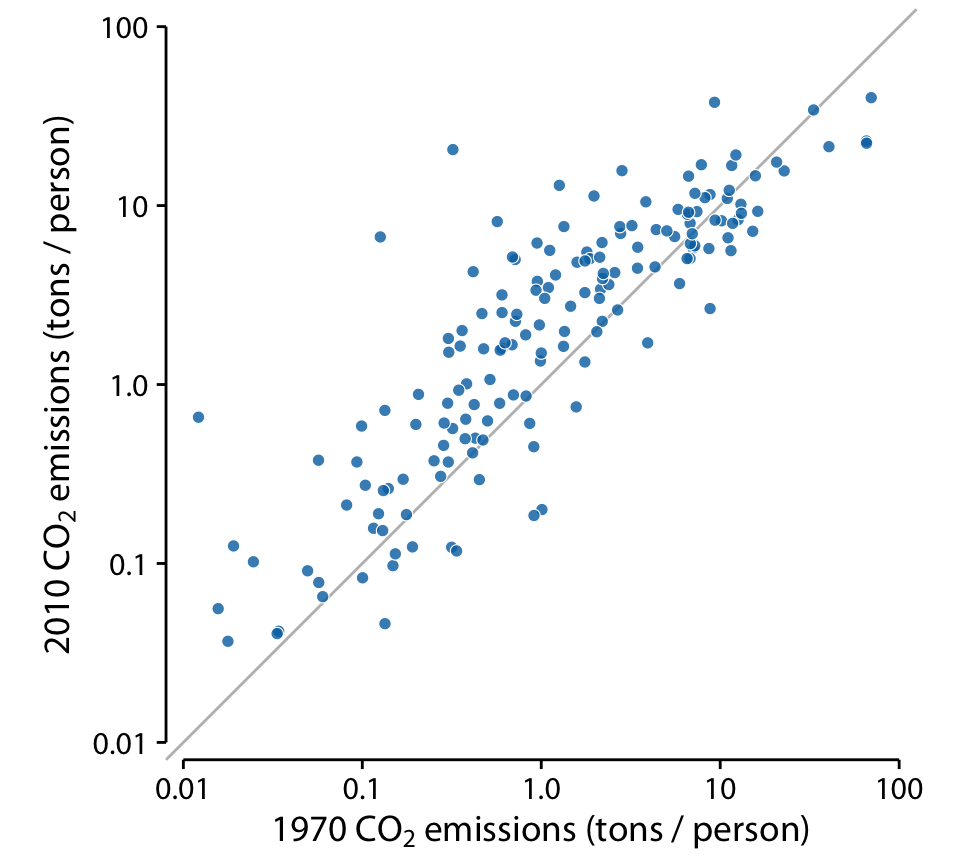
첫째, 대부분의 점들이 대각선에 상대적으로 가깝습니다. 국가 간 CO2 배출량은 거의 네 자릿수 차이가 나지만, 각 국가 내에서 40년간의 배출량은 비교적 일관성이 있습니다. 둘째, 점들이 대각선에 대해 체계적으로 위로 이동해 있습니다. 대부분의 국가에서 40년 동안 CO2 배출량이 증가한 것을 알 수 있습니다.

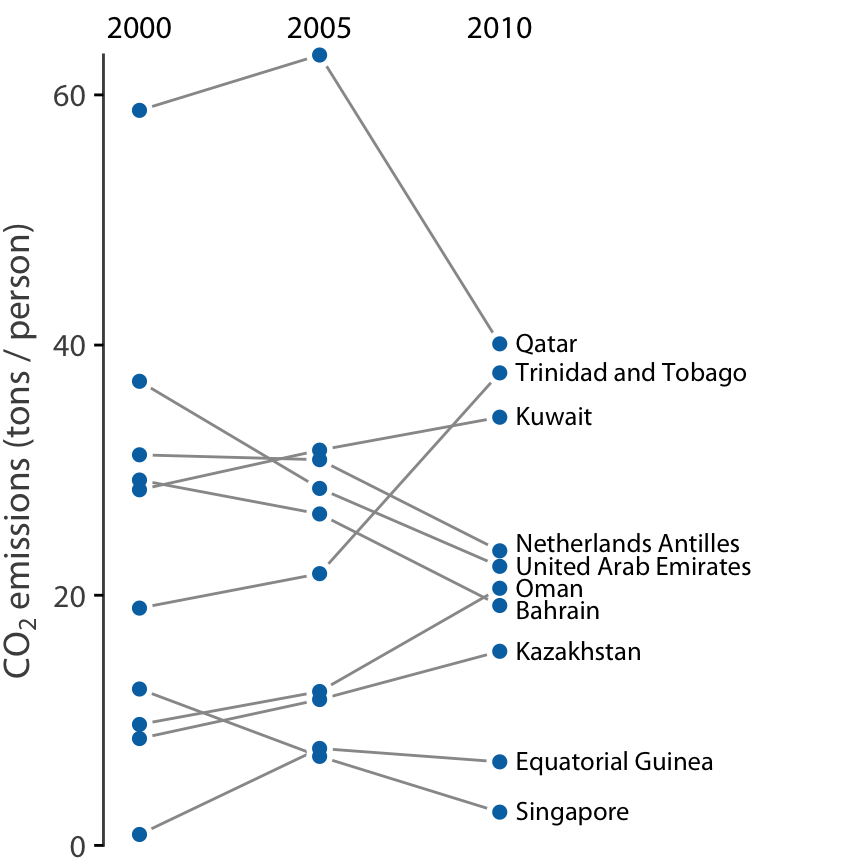
그러나 관측치가 적고 각 개별 사례의 정체성에 더 관심이 있는 경우에는 경사그래프가 더 나은 선택일 수 있습니다. 경사그래프에서는 개별 측정값을 두 개의 열로 정렬된 점으로 나타내고, 짝지어진 점들을 선으로 연결하여 변화를 강조합니다.

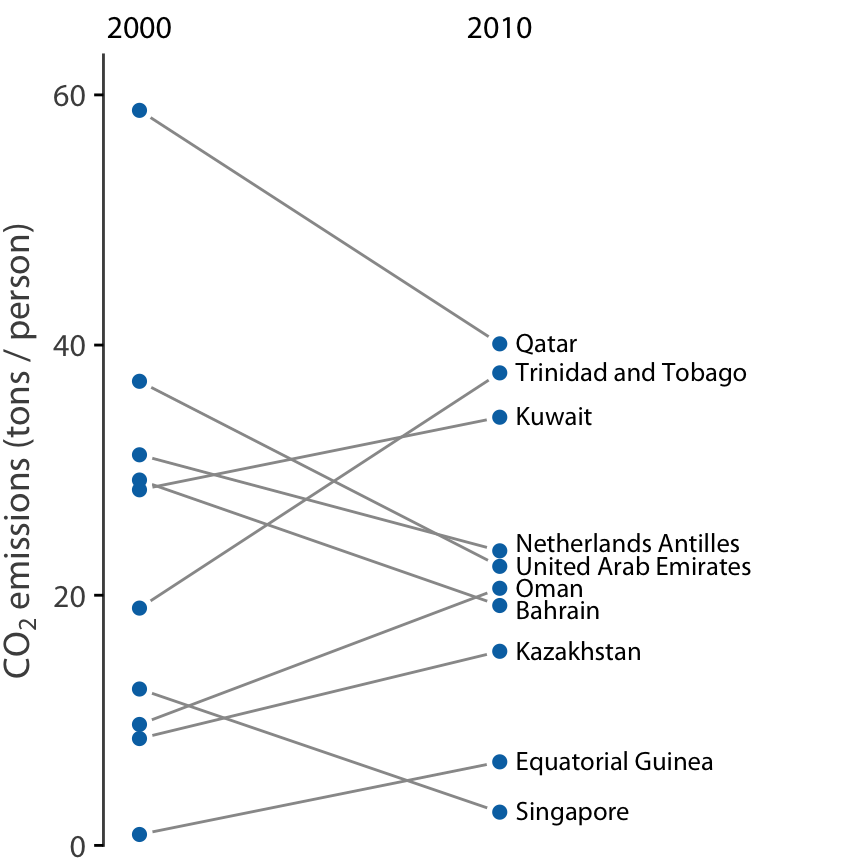
경사그래프의 중요한 장점 중 하나는 산점도와 달리 두 개 이상의 측정을 동시에 비교할 수 있다는 점입니다. 2000년, 2005년, 2010년의 세 시점에서의 CO2 배출량을 보여줄 수 있습니다. 이렇게 하면 전체 10년 동안 배출량이 크게 변화한 국가뿐만 아니라, 카타르나 트리니다드 토바고와 같이 첫 번째 5년 동안과 두 번째 5년 동안의 추세에 큰 차이가 있는 국가들도 강조할 수 있습니다.