Chap6_RNN 시계열 학습

6-1. RNN (Recurent Neural Network, 순환신경망)

시퀀스 데이터를 모델링 하기 위해 등장

기존의 뉴럴 네트워크와 다른 점은 ‘기억’(hidden state)을 하는 것.

출처

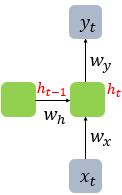
• 첫번째 입력이 들어오면 첫번째 기억이 만들어집니다. 두번째 입력이 들어오면 기존의 기억과 새로운 입력을 참고하여 새 기억을 만듭니다.
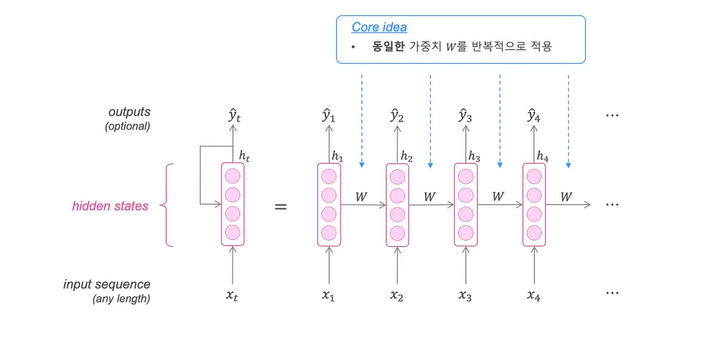
• 입력의 길이만큼 이 과정을 얼마든지 반복할 수 있으며, RNN은 이 요약된 정보를 바탕으로 출력을 만들어 냅니다.
• Core idea: 동일한 가중치 W를 반복적으로 적용.
  → neural network의 문제였던 no symmetry의 문제를 해결.
  
• 장 :
  - 이전 정보를 현재 시점에서 이용하기 때문에 시간에 대한 정보를 추출할 수 있다.
  - 같은 가중치를 반복 사용하기 때문에 가중치 수가 비교적 적다.
• 단 :
  - 같은 가중치를 여러 번 반복 사용하기 때문에 계산 시간이 오래 걸림.
  • 시계열이 깊어질수록 앞의 정보가 점점 흐려짐.
• 유용한 곳 : 주가, 날씨, 텍스트 등 순서가 있는 데이터를 다룰 때

6-2. 데이터 살펴보기

min-max-normalization : 최소-최대 정규화, 값의 범위롤 0~1 사이로 바꾸는 정규화.데이터에 이상치가 있을 경우 적합하지 않음.

6-3. 학습용 데이터 만들기.

넷플릭스 주가 데이터 중 시가, 종가, 최고가, 최저가를 입력으로 하여 다음날의 종가를 예측해보자.

• 배치 단위 : 30일
• 학습용 데이터를 제공하는 Netflix() 클래스 초기화 함수 구현
  - 파이토치의 Dataset()객체는 함수 3개를 제공
  - __init__() : 데이터셋 초기화
  - __len__() : 데이터 개수
  - __getitem__() : 특정 요소 불러오기
  

import numpy as np

from torch.utils.data.dataset import Dataset


class Netflix(Dataset):  # ❶ 클래스 선언
    def __init__(self):
        self.csv = pd.read_csv("/content/drive/MyDrive/Colab Notebooks/data/CH06.csv")        # ❷ 데이터 읽기

        # 입력 데이터 정규화
        self.data = self.csv.iloc[:, 1:4].values   # ❸ 종가를 제외한 데이터
        self.data = self.data / np.max(self.data)  # ➍ 0과 1 사이로 min-max 정규화

        # ➎ 종가 데이터 min-max 정규화
        self.label = data["Close"].values         
        self.label = self.label / np.max(self.label)
    def __len__(self):
        return len(self.data) - 30 # ❶ 사용 가능한 배치 개수

    # 하나의 배치는 30개의 시점을 포함함. --> 입력데이터와 종가 데이터를 30일치씩 읽어온다.
    def __getitem__(self, i):
        data = self.data[i:i+30] # ❶ 입력 데이터 30일치 읽기
        label = self.label[i+30] # ❷ 종가 데이터 30일치 읽기

        return data, label

• len(self.data) - 30 : 사용 가능한 배치 개수
  배치는 첫 번째 데이터부터 마지막 데이터 방향으로 한 칸(1일치 데이터)씩 이동한다. 여기서 하나의 배치 길이는 30이므로 총 배치 개수는 <데이터의 수 - 배치길이> 가 된다.

6-4. RNN 모델 정의하기

import torch
import torch.nn as nn


class RNN(nn.Module):
   def __init__(self):
       super(RNN, self).__init__()

       self.rnn = nn.RNN(input_size=3, hidden_size=8, num_layers=5,
                         batch_first=True)  # ❶ RNN층의 정의

       # ❷ 주가를 예측하는 MLP층 정의
       self.fc1 = nn.Linear(in_features=240, out_features=64)
       self.fc2 = nn.Linear(in_features=64, out_features=1)

       self.relu = nn.ReLU() # 활성화 함수 정의

• ❶ : RNN층 정의
  • input_size : 입력 텐서의 특징 개수 (개장가, 최고가, 최저가 : 총 3개)
  • hiden_size : RNN층에서 각 시점에서의 차원을 의미. 즉 입력 텐서에 가중치를 적용해 특징을 추출함. 주로 8을 사용하는듯?
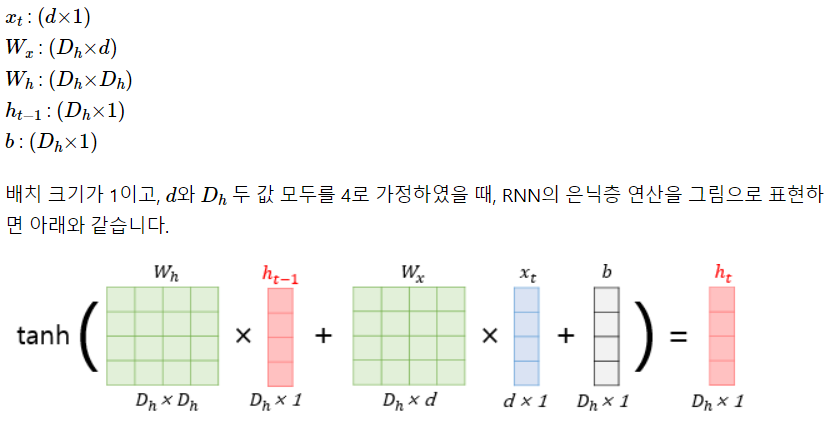
    hidden size는 아래 그림에서 d의 크기를 정해준다고 생각하면 된다.
    
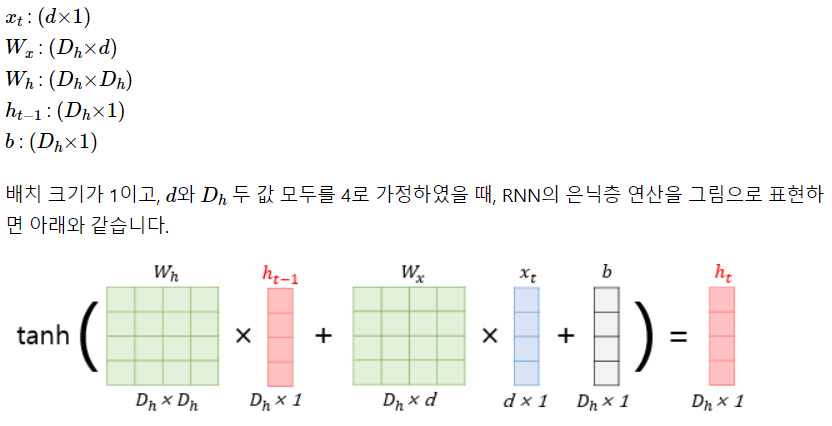
  • num_layers : RNN층을 몇개 쌓을 것인지.
    • 너무 깊으면 -> 기울기 소실 문제 발생
      --> 주로 3 or 5개 쌓음
      
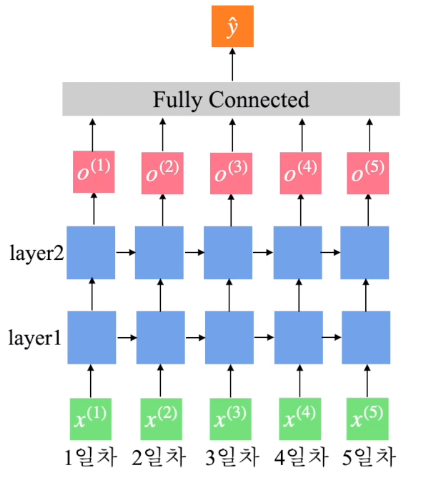
      위 사진은 RNN층을 2개 쌓은 예시
      
  • batch_first : 배치 차원이 가장 앞으로 오게 하는 것. (여기서 배치 차원은 32)
    • True --> 배치 차원이 가장 앞에 오게 됨. --> (32, 30, 3) 모양의 텐서가 됨.
    • False --> 배치 차원이 가장 뒤에 오게 됨. --> (30, 3, 32) 모양의 텐서가 됨.
      --> RNN에서는 True 해야함.
• ❷ : 주가를 예측하는 MLP층 정의
  • ❓왜 fc1의 in_features는 240일까❓
    • 이 예제에서는 마지막 RNN층의 은닉 상태만을 이용하여 주가를 예측함
      --> 마지막 층에 존재하는 30개의 시점 각각에는 8개의 hidden state가 존재하므로 30*8 = 240개가 MLP층의 input으로 들어가게된다.

   def forward(self, x, h0):
       x, hn = self.rnn(x, h0)  # ❶ RNN층의 출력

       # ❷ MLP층의 입력으로 사용될 수 있도록 모양 변경
       x = torch.reshape(x, (x.shape[0], -1))

       # MLP 층을 이용해 종가를 예측
       x = self.fc1(x)
       x = self.relu(x)
       x = self.fc2(x)
      
       # 예측한 종가를 1차원 벡터로 표현
       x = torch.flatten(x)

       return x

• ❶ : 파이토치의 RNN층은 출력값이 2개.

  • 첫번째 출력 값 x : 마지막 RNN층의 은닉 상태 반환
  • 두번째 출력값 hn : 모든 RNN층들의 은닉 상태 반환
    --> 이 예제에서는 마지막 RNN층의 은닉 상태만을 사용하여 주가를 예측할것임.

• ❷ : RNN층의 출력은 (배치크기, 시계열 길이, hidden size)이다.
  MLP층의 입력으로 사용하려면 (배치크기, 시계열 길이 * hidden_size)으로 모양을 변경해야한다.

  reshape(tensor, shape) : tensor를 shape 모양이 되도록 변환

  • MLP층을 거친 후 출력 모양은 (배치개수, 1)이 된다.

6-5. 모델 학습하기

6-5-1. 모델과 데이터셋 정의

import tqdm

from torch.optim.adam import Adam
from torch.utils.data.dataloader import DataLoader

device = "cuda" if torch.cuda.is_available() else "cpu"

model = RNN().to(device)  # 모델의 정의
dataset = Netflix()  # 데이터셋의 정의

6-5-2. 데이터 로더 정의

loader = DataLoader(dataset, batch_size=32)  # 배치 크기를 32로 설정

6-5-3. 최적화 정의

optim = Adam(params=model.parameters(), lr=0.0001) # 사용할 최적화를 설정

6-5-4. 학습 루프 정의

for epoch in range(200):
   iterator = tqdm.tqdm(loader)
   for data, label in iterator:
       optim.zero_grad()

       # ❶ 초기 은닉 상태
       h0 = torch.zeros(5, data.shape[0], 8).to(device)

       # ❷ 모델의 예측값
       pred = model(data.type(torch.FloatTensor).to(device), h0)

       # ❸ 손실의 계산
       loss = nn.MSELoss()(pred,
                           label.type(torch.FloatTensor).to(device))
       loss.backward()  # 오차 역전파
       optim.step()  # 최적화 진행

       iterator.set_description(f"epoch{epoch} loss:{loss.item()}")

torch.save(model.state_dict(), "./rnn.pth")  # 모델 저장

• ❶ : 초기 은닉 상태
  • 모든 요소가 0으로 구성된 텐서로 설정
    zeros(A) : A모양을 갖는 텐서 반환. 이때 모든 요소는 0으로 채움.
  • 은닉층 모양 : (RNN 은닉층 개수, 배치 크기 , 출력 차원) = (5, 32, 8)

6-6. 모델 성능 평가하기

import matplotlib.pyplot as plt

loader = DataLoader(dataset, batch_size=1)  # 예측값을 위한 데이터 로더

preds = []  # 예측값들을 저장하는 리스트
total_loss = 0

with torch.no_grad():
   # 모델의 가중치 불러오기
   model.load_state_dict(torch.load("rnn.pth", map_location=device))

   for data, label in loader:
       h0 = torch.zeros(5, data.shape[0], 8).to(device)  # ➊초기 은닉상태 정의

       # 모델의 예측값 출력
       pred = model(data.type(torch.FloatTensor).to(device), h0)
       preds.append(pred.item())  # ➋예측값을 리스트에 추가
       loss = nn.MSELoss()(pred,
                           label.type(torch.FloatTensor).to(device))  # 손실계산
       total_loss += loss/len(loader)  # ➌손실의 평균치 계산

total_loss.item()

--> total_loss : 0.00125...

6-7. 그래프로 확인

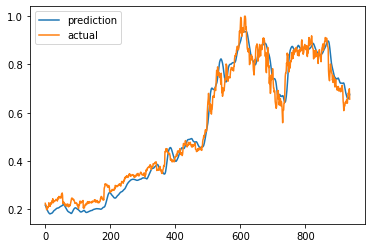
plt.plot(preds, label="prediction")
plt.plot(dataset.label[30:], label="actual")
plt.legend()
plt.show()

전체코드