Word2Vec
Word2Vec
배경
- one-hot vector : 단어 간 유사도 표현 불가
Sparse Representation
- vector(벡터) 또는 matrix(행렬)의 값이 대부분 0으로 표현
- one-hot vector
- 벡터의 차원 == 단어 집합(vocabulary)의 크기
- 고차원에 각 차원이 분리된 표현 방법
Distributed Representation
- 가정(분포 가설) : 비슷한 위치에서 등장하는 단어들은 비슷한 의미를 가짐
- 희소 표현보다 저차원에 단어의 의미를 여러 차원에 분산 표현
Word2Vec
- word features 의 분산 표현 단어 벡터
- 개별단어 문맥 표현 가능

CBOW(Continuous Bag of Words)
- 주변 단어로 중심 단어 예측
- 슬라이딩 윈도우(sliding window) 기법으로 창을 계속 이동하여 중심단어와 주변단어를 바꿔가며 학습
- input layer의 input으로 윈도우 안의 주변 단어들의 one-hot vector가 들어감
- hidden layer(은닉층)가 1개 이기 떄문에 Deep Neural Network(심층신경망)이 아닌 Shallow Neural Network(얕은신경망)
- 은닉층에는 activation function(활성화 함수)이 존재하지 않음
- 은닉층 : Lookup table(Projection Layer, 투사층), 연산 담당 층
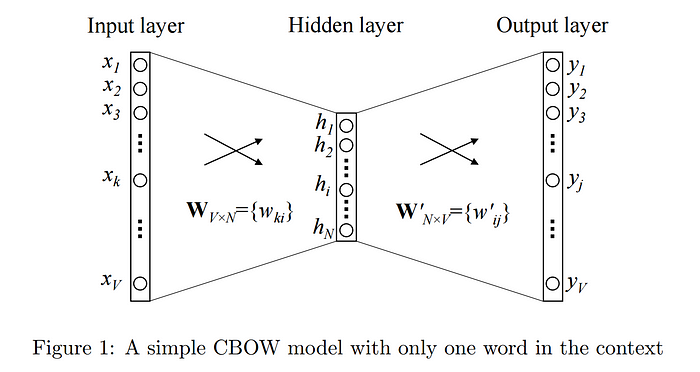
- 투사층의 크기 (M) : 임베딩하고 난 벡터의 차원
- 입력층-투사층 사이 가중치(W) : V * M 행렬
- 투사층-출력층 사이 가중치(W') : M * V 행렬
- V : 단어 집합 크기
- W, W' : 랜덤 초기화, 학습해나가는 구조
- x : 주변 단어의 one-hot vector(input)
- lookup : 을 읽어오는 것 ( )
- lookup 해온 W의 row vector가 Word2Vec 수행 후 각 단어의 M차원 크기를 갖는 임베딩 벡터들
- W(가중치)가 곱해져 생긴 결과 벡터들은 투사층에서 만나 이 벡터들의 평균 벡터를 구하게됨(Skip-gram과 차이점 - input이 중심단어 하나)
- 평균 벡터는 W'와 곱해짐(두번째 가중치 행렬)
- one-hot vector의 차원(V)과 같은 벡터
- softmax 함수를 통과해 score vector가 나옴
- 스코어 벡터(j번째 인덱스가 가진 0~1사이 값, ) : j번째 단어가 중심 단어일 확률
- 중심 단어를 y로 했을 때 loss function(손실함수)로 cross-entropy 함수 사용
- cross-entropy 함수 input : one-hot vector, score vector
- 정확 예측 : , 가 y를 정확히 예측, -1 log(1) = 0, cross-entropy = 0
- Back Propagation(역전파)로 W, W' 학습, M차원의 크기를 갖는 W의 행이나 W'의 열에서 어느것을 임베딩 벡터로 사용할지 결정 또는 W와 W'의 평균치로 임베딩 벡터 선택, 두 행렬을 하나의 행렬로 취급(tied) 하는 방식으로 학습 진행 가능(학습이 잘 되면 어느 것을 선택해도 무관)
Skip-gram
- 중심 단어로 주변 단어 예측
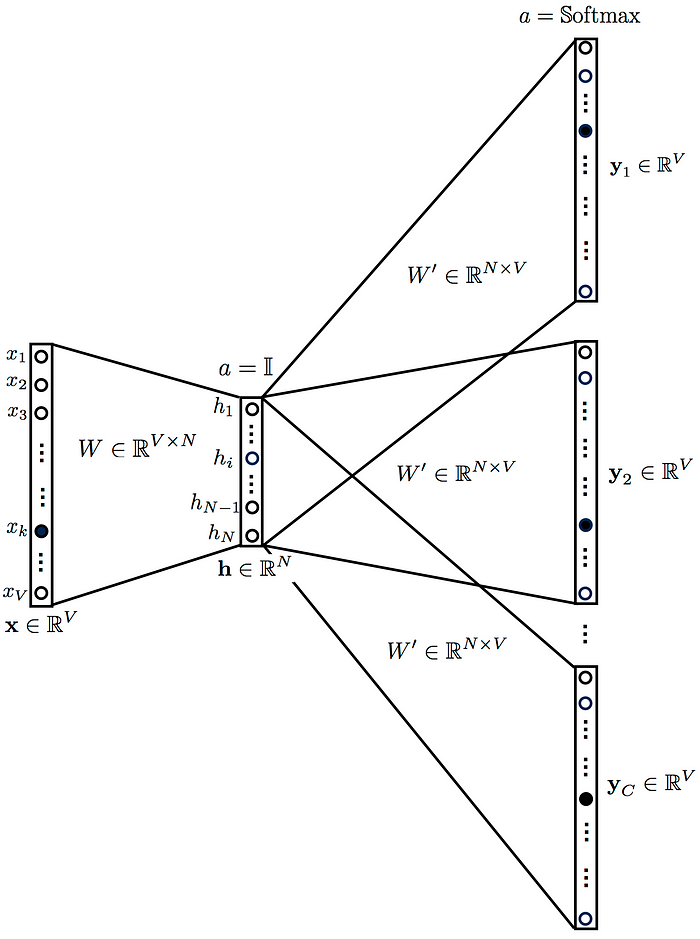
- 인공신경망 도식화
- 투사층 평균 구하는 과정 없음
CBOW vs Skip-gram
- CBOW : 빠름, 자주 나오는 단어에 대해 더 잘 표현
- Skip-gram : 적은 양의 데이터에 잘 작동, 드문 단어에 잘 작동
NNLM vs Word2Vec
- NNLM(피드 포워드 신경망 언어 모델)
- 언어 모델 : 다음 단어 예측 ⇒ 이전 단어들만 참고
- 연산량 :
- Word2Vec
- 워드 임베딩 목적 ⇒ 중심 단어 예측 ⇒ 전후 단어 참고
- 은닉층 제거(투사층 바로 다음 출력층)
- 연산량 :
- 대표 기법 : hierarchical softmax(계층적 소프트맥스), negative sampling
- 워드 임베딩 목적 ⇒ 중심 단어 예측 ⇒ 전후 단어 참고
- n : 학습에 사용하는 단어 수
- m : 임베딩 벡터의 차원
- h : 은닉층 크기
- V : 단어 집합의 크기
Word2 Vec 학습 트릭
Negative Sampling
- Word2Vec 출력층에서 |소프트맥스 함수 지난 단어 집합 크기 벡터 - 원-핫 벡터|, 임베딩 테이블의 모든 단어 임베딩 벡터 값 업데이트 ⇒ 무거운 작업
- 역전파 과정 시 무관 단어 임베딩 벡터값 업데이트 ⇒ 비효율적
- 네거티브 샘플링
- 일부 단어 집합에만 집중하는 기법
- 전체 단어 집합보다 훨씬 작은 단어 집합중 마지막 단계를 이진 분류 문제로 변환
- 목적 함수
- negative sampling의 기본 아이디어
- noise contrastive estimation 개념에 기초(GAN과 유사, 로지스틱 회귀를 통해 가짜 신호를 진짜와 구별하는 것이 좋은 모델임을 유지)
- SGD와 유사
- 모든것을 보지 않고 K개만 관측해 계산 효율성 증가(negative sample의 숫자에 의존)
- SGD와 차이점
- 한 번의 관측이지만 K개를 보는 점
- noise distribution 을 확률분포로 사용
- noise distribution을 사용하는 이유 : the challenge to distinguish real data from the fake data we’re trying to solve
- 적절한 noise distribution은 unigram distribution 이다
- 와 같의 정의
- 3/4 : 실험 값
- f(w) : corpus에서 단어의 빈도수
- negative sample : not context words
- positive sample : context words
Skip-Gram with Negative Sampling, SGNS
- 기존
- 중심 단어로 주변 단어 예측
- Negative sampling
- 중심, 주변 단어로 윈도우 크기내 존재하는 이웃 인지 확률 예측
- Skip-gram → SGNS
- label 1 : 이웃
- label 0 : 이웃 x
- 두 임베딩 테이블 : 훈련 데이터 단어 집합 크기(같은 크기)
- 입력1 중심단어 룩업테이블(임베딩 벡터)
- 입력2 주변단어 룩업테이블(임베딩 벡터)
- 임베딩 벡터 변환 후 연산
- 모델 예측 값 : (내적)
- 레이블과의 오차 ⇒ 역전파 ⇒ 중심단어-주변단어 임베딩 벡터값 업데이트
- 선택적으로 두 임베딩 테이블 중 좌측 테이블을 최종 임베딩 테이블로 사용
- 윈도우 내 등장하지 않은 어떤단어 () 가 negative smaple로 뽑힐 확률
subsampling frequent words
- 단어 수 증가에 따라 계산량 폭증
- 자주 등장한 단어는 확률적 방식으로 학습량 줄임(등장 빈도만큼 업데이트 기회 많음)
- i번째 단어(를 학습에서 제외 시키기 위한 확률
- : 해당 단어가 corpus에 등장한 비율(해당 단어 빈도/ 전체 단어수)
- t : 사용자 지정값, (0.00001 권장)
- 이 0.01(높은 빈도 단어
- ex) 조사 '은/는'
- : 0.9684 일 때, 100번중 96번 학습 제외
- : 0에 가까우면 거의 항상 학습
- 학습량 줄여 계산량 감소 시킴
- negative sampling과 subsampling에 쓰는 확률값은 고정 ⇒ 학습 시작시 미리 계산
Hierarchical Softmax
- leaf가 words인 binary tree 이용
- index가 j 인 j번쨰 단어의 확률 leaf와 output softmax vector의 j번째 위치
- 확률질량함수의 곱으로 루트노드부터 각 단어까지 도달하는 경로를 간단한 시그모이드 함수의 사용으로 표현 가능 하다면
- : 루트노드에서 w(계산하려는 확률 질량)까지 가는 경로에서 j번째 노드
- 일반적으로 확률을 시그모이드표현으로 대체한다
- 각각의 inner node에 대해 임의의 자식노드(왼쪽 또는 오른쪽)를 선택하고 양의 시그모이드 함수 값을 그들중 하나에 할당
- 이러한 사항을 보존하면서 시그모이드 함수는 다음과 같이 표현
- node n 의 우측 자식 노드에 대해 유사하게 표현
- 이전 모든 단계에 대해 좌측 또는 우측 임의의 노드 케이스에 대해 불린체킹을 하는 마지막 함수 계산을 모아보면 다음과 같다.
-
<> : boolean checking
-
L(w) : 트리의 깊이
-
ch(n) : n노드의 자식
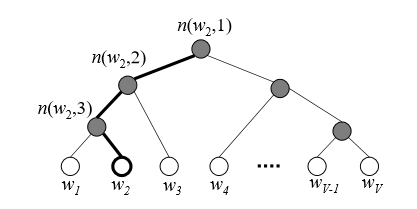
-
루트노드, 2개의 inner node, leaf 노드가 있다면 3단계의 계산을 하고 계산량을 상당히 줄여줌
-
Word2Vec 목적함수
- Distributianal Hypothesis에 근거한 방법론
- o : 주변단어(context word)
- c : 중심단어(center word)
- p(o|c) : 중심단어(c)가 주어졌을 때 주변단어(o)가 등장할 조건부 확률
- v : 중심 단어 벡터
- u : 주변 단어 벡터
- 임베딩이 잘 되어있으면 u,v 어느 것 사용해도 무방
Word2Vec train visualization

Reference
https://ratsgo.github.io/from frequency to semantics/2017/03/11/embedding/
https://ratsgo.github.io/from frequency to semantics/2017/03/30/word2vec/
https://dreamgonfly.github.io/
https://en.wikipedia.org/wiki/Word2vec
https://www.analyticsvidhya.com/blog/2021/07/word2vec-for-word-embeddings-a-beginners-guide/
https://towardsdatascience.com/introduction-to-word-embedding-and-word2vec-652d0c2060fa















