# 본 자료는 이수안 교수님(https://suanlab.com/)의 자료를 기반으로 수정 및 보완하여 제작되었습니다.
# 제작자 : 김민수(rlaalstn1504@naver.com)

컨볼루션 신경망(Convolution Neural Networks, CNN)

• 완전 연결 네트워크의 문제점으로부터 시작

  • 매개변수의 폭발적인 증가
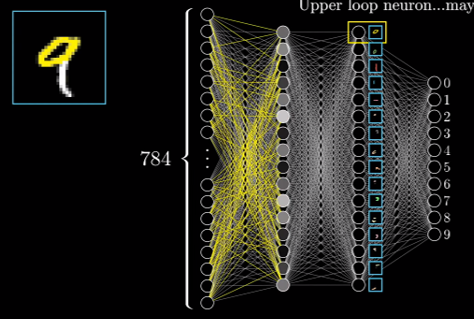
  • 공간 추론의 부족: 픽셀 사이의 근접성 개념이 완전 연결 계층(Fully-Connected Layer)에서는 손실됨
  

• 동물의 시각피질의 구조에서 영감을 받아 만들어진 딥러닝 신경망 모델

• 시각 자극이 1차 시각피질을 통해서 처리된 다음, 2차 시각피질을 경유하여, 3차 시각피질 등 여러 영역을 통과하여 계층적인 정보처리

• 정보가 계층적으로 처리되어 가면서 점차 추상적인 특징이 추출되어 시각 인식

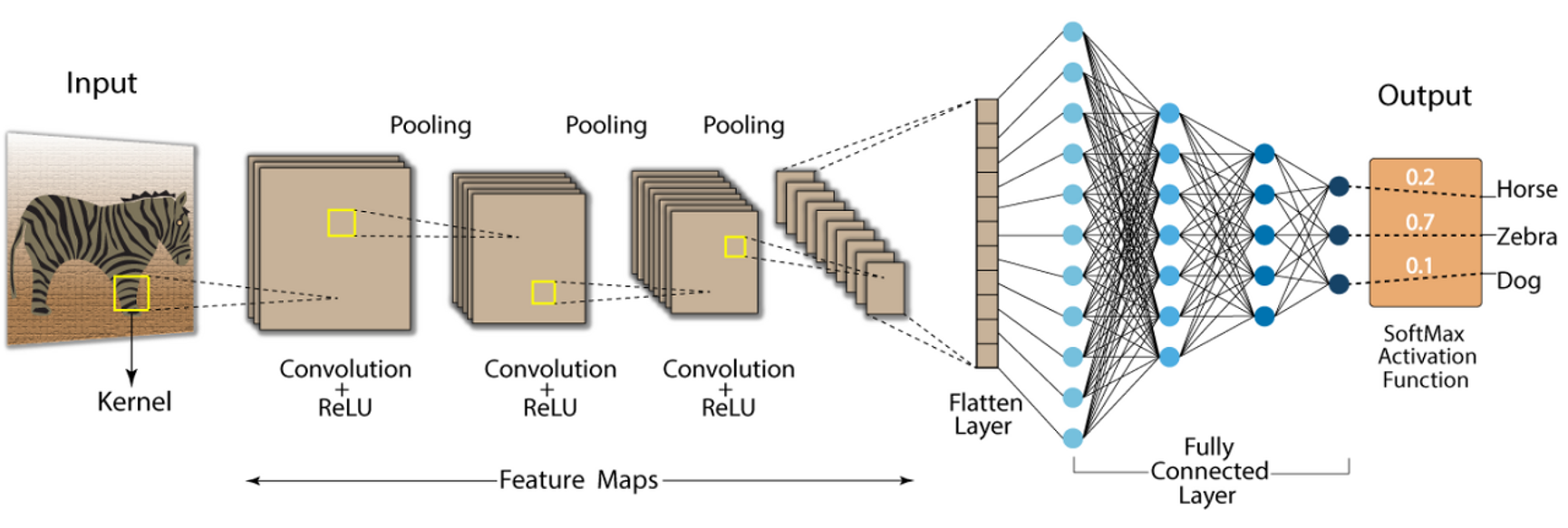
• 동물의 계층적 특징 추출과 시각인식 체계를 참조하여 만들어진 모델

  • 전반부 : 컨볼루션 연산을 수행하여 특징 추출
  • 후반부 : 특징을 이용하여 분류

• 영상분류, 문자 인식 등 인식문제에 높은 성능

  

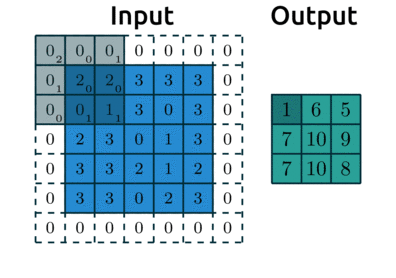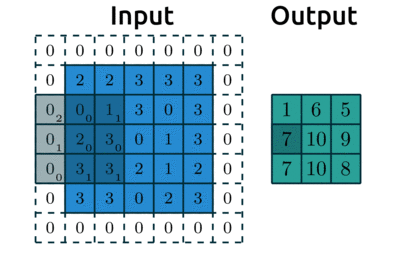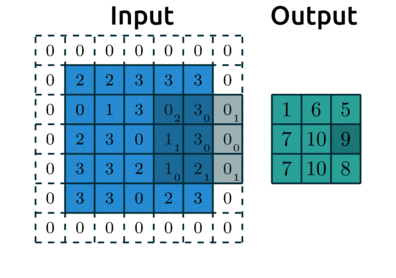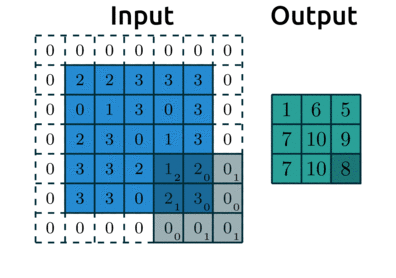
컨볼루션 연산 (Convolution Operation)

• 필터(filter) 연산

  • 입력 데이터에 필터를 통한 어떠한 연산을 진행
  • 필터에 대응하는 원소끼리 곱하고, 그 합을 구함
  • 연산이 완료된 결과 데이터를 특징 맵(feature map)이라 부름

• 필터(filter)

  • 커널(kernel)이라고도 함
  • 이미지 처리에서 사용하는 '이미지 필터'와 비슷한 개념
  • 필터의 사이즈는 거의 항상 홀수
    • SAME 패딩을 사용하여 입력과 출력의 크기를 동일하게 유지하기 쉬움
    • 중심위치가 존재, 즉 구별된 하나의 픽셀(중심 픽셀)이 존재
  • 필터의 학습 파라미터 개수는 입력 데이터의 크기와 상관없이 일정
  • 과적합을 방지할 수 있음
  

• 연산 시각화

  

• 일반적으로, 합성곱 연산을 한 후의 데이터 사이즈

  $\quad (n-f+1) \times (n-f+1)$

  $n$: 입력 데이터의 크기
  $f$: 필터(커널)의 크기

  

• 위 예에서 입력 데이터 크기($n$)는 5, 필터의 크기($k$)는 3이므로 출력 데이터의 크기는 $(5 - 3 + 1) = 3$

필터가 이미지의 특징을 추출하는 과정 (sobel 필터를 예시로)

Sobel 필터란?

• Sobel 필터는 수학적으로 이미지의 밝기 변화(Gradient)를 계산하는 필터임

• 두 가지 종류가 있음:

  • 수평선 검출 필터: 이미지에서 수평 방향의 변화를 감지.
  • 수직선 검출 필터: 이미지에서 수직 방향의 변화를 감지.

• Sobel 필터를 활용하면 CNN에서 필터가 특징을 추출하는 과정을 직관적으로 이해할 수 있음.

• Sobel 필터는 가장 간단한 에지 검출 필터 중 하나로, 이미지에서 선(에지)을 강조함.

  

  이미지출처: https://www.researchgate.net/figure/Sobel-filter-using-two-33-kernels-Gx-Gy_fig5_375105942

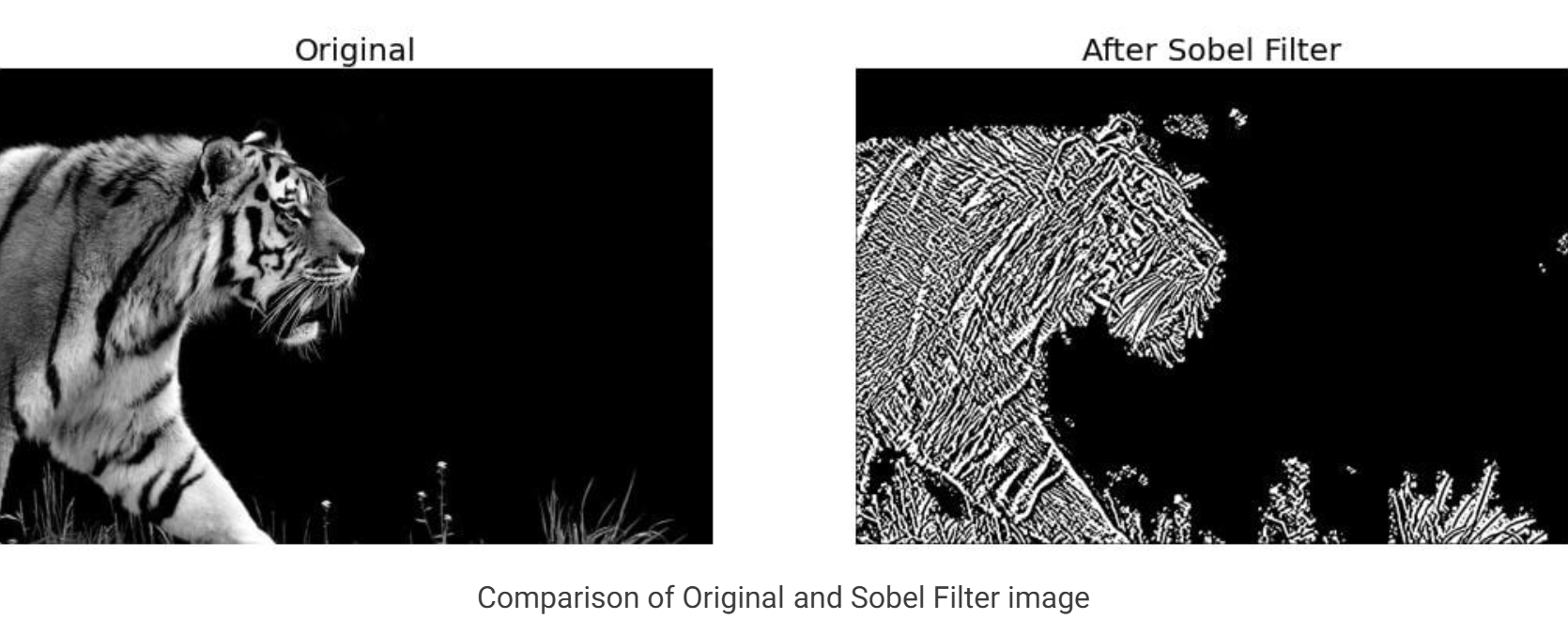
이미지출처: https://learnopencv.com/edge-detection-using-opencv/

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_sample_image

from tensorflow.keras.layers import Conv2D

flower = load_sample_image('flower.jpg') / 255
print(flower.dtype)
print(flower.shape)
plt.imshow(flower)
plt.show()

float64
(427, 640, 3)

china = load_sample_image('china.jpg') / 255
print(china.dtype)
print(china.shape)
plt.imshow(china)
plt.show()

float64
(427, 640, 3)

images = np.array([china, flower])
batch_size, height, width, channels = images.shape
print(images.shape)

(2, 427, 640, 3)

# 컨볼루션 연산을 수행할 필터를 직접 생성
filters = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filters[:, 3, :, 0] = 1 # 첫 번째 필터 세로줄 형성
filters[3, :, :, 0] = 1 # 첫 번째 필터 가로줄 형성
filters[3, 3, :, 1] = 1 # 두 번째 필터 중심점 형성

print(filters.shape)

(7, 7, 3, 2)

# 필터가 학습을 통해 자동으로 생성되는 CNN 레이어 생성
convolve = Conv2D(filters=16, kernel_size=7, activation='relu')

패딩(Padding)과 스트라이드(Stride)

• 필터(커널) 사이즈과 함께 입력 이미지와 출력 이미지의 사이즈를 결정하기 위해 사용
• 사용자가 결정할 수 있음

패딩(Padding)

• 입력 데이터의 주변을 특정 값으로 채우는 기법

  • 주로 0으로 많이 채움
  

• 출력 데이터의 크기

  $\quad (n+2p-f+1) \times (n+2p-f+1)$

  • 위 그림에서, 입력 데이터의 크기($n$)는 5, 필터의 크기($f$)는 3, 패딩값($p$)은 1이므로 출력 데이터의 크기는 ($5 + 2\times 1 - 3 + 1) = 5$

• valid

  • 패딩을 주지 않음
  • padding=0은 0으로 채워진 테두리가 아니라 패딩을 주지 않는다는 의미

• same

  • 패딩을 주어 입력 이미지의 크기와 연산 후의 이미지 크기를 같도록 유지
  • 만약, 필터(커널)의 크기가 $k$ 이면, 패딩의 크기는 $p = \frac{k-1}{2}$ (단, stride=1)

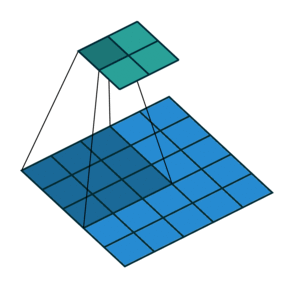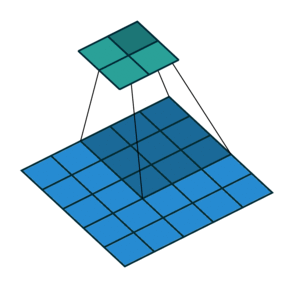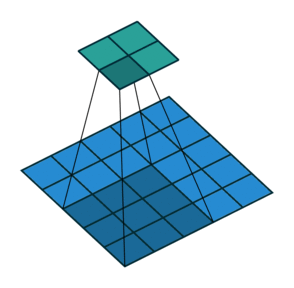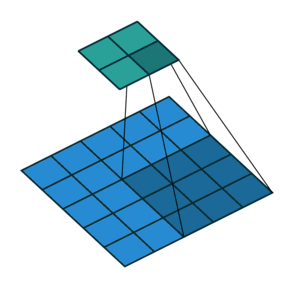
스트라이드(Stride)

• 필터를 적용하는 간격을 의미

• 아래 예제 그림은 간격이 2

  

출력 데이터의 크기

$\qquad OH = \frac{H + 2P - FH}{S} + 1 $

$\qquad OW = \frac{W + 2P - FW}{S} + 1 $

• 입력 크기 : $(H, W)$

• 필터 크기 : $(FH, FW)$

• 출력 크기 : $(OH, OW)$

• 패딩, 스트라이드 : $P, S$

• 위 식의 값에서 $\frac{H + 2P - FH}{S}$ 또는 $\frac{W + 2P - FW}{S}$가 정수로 나누어 떨어지는 값이어야 함

• 정수로 나누어 떨어지지 않으면, 패딩, 스트라이드 값을 조정하여 정수로 나누어 떨어지게 해야함

conv = Conv2D(filters=16, kernel_size=3,padding='same',strides=1, activation='relu')

풀링(Pooling)

• 필터(커널) 사이즈 내에서 특정 값을 추출하는 과정

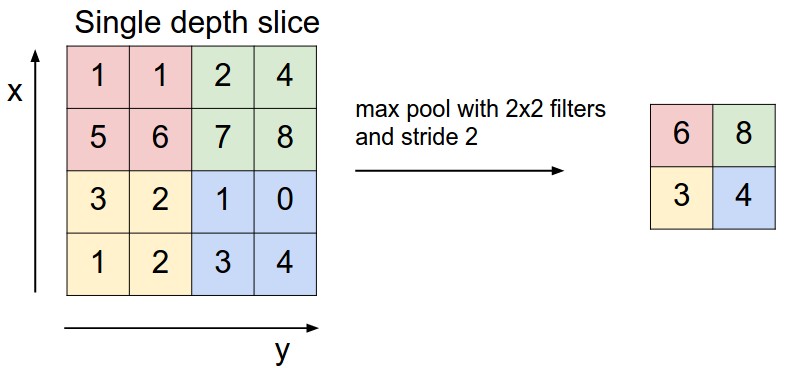
맥스 풀링(Max Pooling)

• 가장 많이 사용되는 방법

• 출력 데이터의 사이즈 계산은 컨볼루션 연산과 동일

  $\quad OH = \frac{H + 2P - FH}{S} + 1 $

  $\quad OW = \frac{W + 2P - FW}{S} + 1 $

• 일반적으로 stride=2, kernel_size=2 를 통해 특징맵의 크기를 절반으로 줄이는 역할

• 모델이 물체의 주요한 특징을 학습할 수 있도록 해주며, 컨볼루션 신경망이 이동 불변성 특성을 가지게 해줌

• 예를 들어, 아래의 그림에서 초록색 사각형 안에 있는 2와 8의 위치를 바꾼다해도 맥스 풀링 연산은 8을 추출

• 모델의 파라미터 개수를 줄여주고, 연산 속도를 빠르게 함

  

from tensorflow.keras.layers import MaxPooling2D

print(flower.shape)
flower = np.expand_dims(flower, axis=0)
print(flower.shape)

output = Conv2D(filters=32, kernel_size=3, strides=1, padding='same',activation='relu')(flower)
print(output.shape) # 아직 학습되지 않아 랜덤한 숫자로 초기화된 필터를 거친 연산 결과

output = MaxPooling2D(pool_size=2)(output)
print(output.shape)

(427, 640, 3)
(1, 427, 640, 3)
(1, 427, 640, 32)
(1, 213, 320, 32)

plt.imshow(output[0,:,:,8],cmap='gray')
plt.show()

평균 풀링(Avg Pooling)

• 필터 내의 있는 픽셀값의 평균을 구하는 과정

• 과거에 많이 사용, 요즘은 잘 사용되지 않음

• 맥스풀링과 마찬가지로 stride=2, kernel_size=2 를 통해 특징 맵의 사이즈를 줄이는 역할

  

from tensorflow.keras.layers import AvgPool2D

print(flower.shape)
output = Conv2D(filters=32, kernel_size=3, strides=1, padding='same',activation='relu')(flower)
output = AvgPool2D(pool_size=2)(output)
print(output.shape)

(1, 427, 640, 3)
(1, 213, 320, 32)

plt.imshow(output[0,:,:,2], cmap='gray')
plt.show()

전역 평균 풀링(Global Avg Pooling)

• 특징 맵 각각의 평균값을 출력하는 것이므로, 특성맵에 있는 대부분의 정보를 잃음
• 출력층에는 유용할 수 있음

from tensorflow.keras.layers import GlobalAvgPool2D

print(flower.shape)
output = Conv2D(filters=32, kernel_size=3, strides=1, padding='same',activation='relu')(flower)
print(output.shape)
output = GlobalAvgPool2D()(output)
print(output.shape)

(1, 427, 640, 3)
(1, 427, 640, 32)
(1, 32)

완전 연결 계층(Fully-Connected Layer)

• 입력으로 받은 텐서를 1차원으로 평면화(flatten) 함
• 밀집 계층(Dense Layer)라고도 함
• 일반적으로 분류기로서 네트워크의 마지막 계층에서 사용

from tensorflow.keras.layers import Dense

output_size = 1000

fc = Dense(units=output_size, activation='softmax')

유효 수용 영역(ERF, Effective Receptive Field)

• 입력 이미지에서 특정 뉴런의 활성화(결과)에 영향을 미치는 이미지의 영역

• 네트워크가 깊어지면 더 많은 필터와 연산이 겹쳐져, 뉴런이 이미지를 "망원경"으로 보는 것처럼 더 넓은 영역을 고려하게 됨

• 따라서 깊은 계층에서는 입력 이미지의 "멀리 떨어진" 부분까지 고려해 특징을 학습할 수 있음

• 유효 수용 영역이 크면 더 복잡하고 넓은 관계(예: 얼굴 전체 구조)를 학습할 수 있으며, 너무 작으면, 작은 패턴(예: 한 부분의 점, 선)만 학습하여 전반적인 구조를 이해하지 못할 수 있음

  

• RF의 중앙에 위치한 픽셀은 주변에 있는 픽셀보다 더 높은 가중치를 가짐

  • 중앙부에 위치한 픽셀은 여러 개의 계층을 전파한 값
  • 중앙부에 있는 픽셀은 주변에 위치한 픽셀보다 더 많은 정보를 가짐

• 가우시안 분포를 따름

  

CNN 모델 학습

MNIST (LeNet)

• Yann LeCun 등의 제안(1998)

• 5 계층 구조: Conv-Pool-Conv- Pool-Conv-FC-FC(SM)

• 입력 : 32x32 필기체 숫자 영상 (MNIST 데이터)

• 풀링 : 가중치x(2x2블록의 합) + 편차항

• 시그모이드 활성화 함수 사용

• 성능: 오차율 0.95%(정확도: 99.05%)

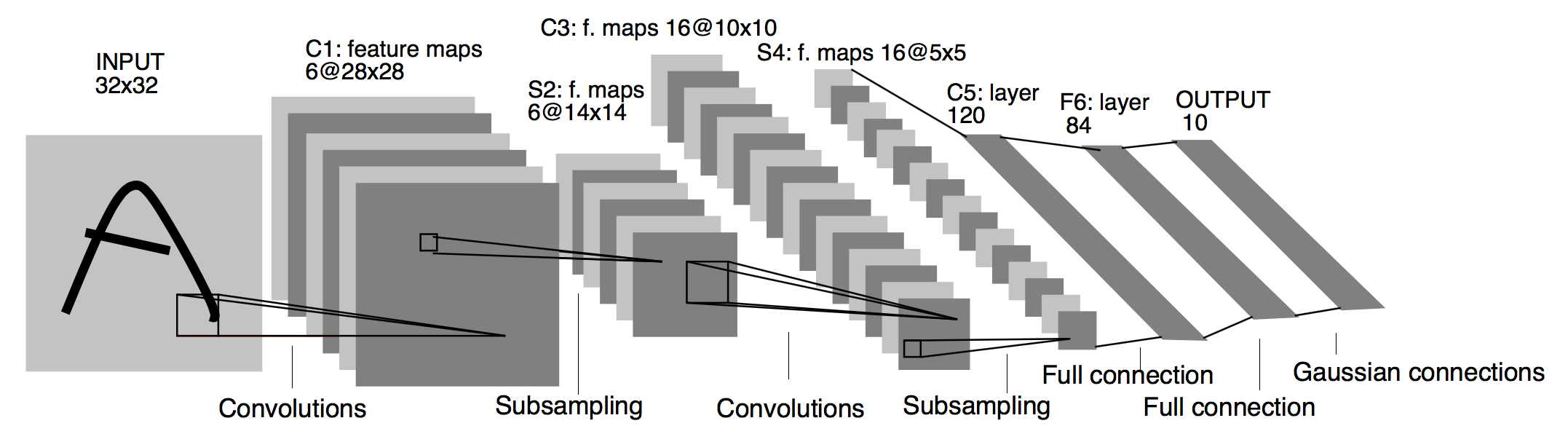  [LeNet-5 구조]

모듈 임포트

from tensorflow.keras import Model
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense
from tensorflow.keras.callbacks import EarlyStopping, TensorBoard
from tensorflow.keras.datasets import mnist

import matplotlib.pyplot as plt
import numpy as np

데이터 로드 및 전처리

(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train[:,:,:,np.newaxis] / 255.0, x_test[:,:,:,np.newaxis] / 255.0 # 채널 정보가 누락되어 있으므로 축 추가
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)

(60000, 28, 28, 1)
(60000,)
(10000, 28, 28, 1)
(10000,)

plt.imshow(x_train[0,:,:,0], cmap='gray')
print(y_train[0])

5

모델 구성 및 컴파일

num_classes = 10
epochs = 30
batch_size = 32

class LeNet5(Model):
    def __init__(self, num_classes=10):
        # 부모 클래스의 기능을 상속받기 위해 부모 클래스의 초기화 메서드(__init__)를 호출
        super(LeNet5, self).__init__()
        # 첫 번째 합성곱 층: 6개의 필터를 사용하고, 각 필터의 크기는 5x5입니다. 
        # 'same' 패딩을 사용하여 입력 이미지와 출력 이미지의 크기를 동일하게 유지합니다.
        # 활성화 함수로는 ReLU를 사용하여 비선형 변환을 제공합니다.
        self.conv1 = Conv2D(filters=6, kernel_size=5, padding='same', activation='relu')
        
        # 첫 번째 풀링 층: 최대 풀링을 사용하고, 풀링의 크기는 2x2입니다.
        # 이 층은 데이터의 공간 크기를 줄이고, 주요 특징을 유지합니다.
        self.pool1 = MaxPooling2D(pool_size=2)
        
        # 두 번째 합성곱 층: 16개의 필터를 사용하고, 각 필터의 크기는 5x5입니다.
        # 'same' 패딩을 사용하여 입력 이미지와 출력 이미지의 크기를 동일하게 유지합니다.
        # 활성화 함수로는 ReLU를 사용합니다.
        self.conv2 = Conv2D(filters=16, kernel_size=5, padding='same', activation='relu')
        
        # 데이터를 일렬로 펼치는 층입니다. 이 층은 합성곱 층과 풀링 층을 거쳐 얻어진
        # 2차원 특징 맵을 1차원 벡터로 변환하여 완전 연결 층에 전달할 수 있도록 합니다.
        self.flatten = Flatten()
        
        # 첫 번째 완전 연결 층: 120개의 유닛을 가지며, 활성화 함수로 ReLU를 사용합니다.
        # 이 층은 1차원 벡터의 형태로 펼쳐진 데이터를 받아 처리합니다.
        self.fc1 = Dense(units=120, activation='relu')
        
        # 두 번째 완전 연결 층: 84개의 유닛을 가지며, 활성화 함수로 ReLU를 사용합니다.
        self.fc2 = Dense(units=84, activation='relu')
        
        # 출력 층: num_classes 개수의 유닛을 가지며, 각 클래스에 대한 확률을 출력하기 위해
        # 활성화 함수로 softmax를 사용합니다.
        self.fc3 = Dense(units=num_classes, activation='softmax')

    def call(self, input_data):
        # 각 층을 차례대로 호출하여 입력 데이터를 처리합니다.
        x = self.conv1(input_data)  # 첫 번째 합성곱 층을 통과
        x = self.pool1(x)           # 첫 번째 풀링 층을 통과
        x = self.conv2(x)           # 두 번째 합성곱 층을 통과
        x = self.pool1(x)           # 두 번째 풀링 층을 통과 (동일한 풀링 층 재사용)
        x = self.flatten(x)         # 플래튼 층을 통과
        x = self.fc1(x)             # 첫 번째 완전 연결 층을 통과
        x = self.fc2(x)             # 두 번째 완전 연결 층을 통과
        x = self.fc3(x)             # 출력 층을 통과
        return x

model = LeNet5(num_classes=10)

model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

callbacks = [EarlyStopping(patience=3, monitor='val_loss'), TensorBoard(log_dir='./logs', histogram_freq=1)] # histogram_freq=1 : epoch마다 히스토그램 기록

모델 학습 및 평가

model.fit(x_train, y_train,
          batch_size=batch_size,
          epochs=epochs,
          validation_split=0.2,
          callbacks=callbacks)

Epoch 1/30
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 52s 33ms/step - accuracy: 0.8790 - loss: 0.4138 - val_accuracy: 0.9700 - val_loss: 0.0958
Epoch 2/30
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 79s 32ms/step - accuracy: 0.9761 - loss: 0.0724 - val_accuracy: 0.9787 - val_loss: 0.0724
Epoch 3/30
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 79s 29ms/step - accuracy: 0.9857 - loss: 0.0485 - val_accuracy: 0.9855 - val_loss: 0.0482
Epoch 4/30
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 84s 31ms/step - accuracy: 0.9892 - loss: 0.0336 - val_accuracy: 0.9880 - val_loss: 0.0427
Epoch 5/30
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 80s 29ms/step - accuracy: 0.9919 - loss: 0.0254 - val_accuracy: 0.9852 - val_loss: 0.0508
Epoch 6/30
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 82s 30ms/step - accuracy: 0.9939 - loss: 0.0202 - val_accuracy: 0.9874 - val_loss: 0.0451
Epoch 7/30
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 83s 31ms/step - accuracy: 0.9940 - loss: 0.0183 - val_accuracy: 0.9864 - val_loss: 0.0504





<keras.src.callbacks.history.History at 0x7b6eb6a15600>

%load_ext tensorboard

The tensorboard extension is already loaded. To reload it, use:
  %reload_ext tensorboard

%tensorboard --logdir logs

<IPython.core.display.Javascript object>

Fashion MNIST

모듈 임포트

import datetime
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

from tensorflow.keras import Model
from tensorflow.keras.models import Sequential
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.datasets.fashion_mnist import load_data
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout, Input
from tensorflow.keras.callbacks import EarlyStopping, TensorBoard

데이터 로드 및 전처리

(x_train, y_train), (x_test, y_test) = load_data()
x_train, x_test = x_train[:,:,:,np.newaxis] / 255.0, x_test[:,:,:,np.newaxis] / 255

print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)

(60000, 28, 28, 1)
(60000,)
(10000, 28, 28, 1)
(10000,)

class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
               'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']

모델 구성 및 학습

• 임의의 모델

def build_model():
    # 입력 레이어 정의
    input = Input(shape=(28,28,1))
    output = Conv2D(filters=32, kernel_size=3, activation='relu', padding='same')(input)
    output = Conv2D(filters=32, kernel_size=3, activation='relu', padding='same')(output)
    output = Conv2D(filters=32, kernel_size=3, activation='relu', padding='same')(output)

    # 평탄화와 완전 연결 레이어
    output = Flatten()(output)
    output = Dense(128, activation='relu')(output)
    output = Dense(64, activation='relu')(output)

    # 출력 레이어
    output = Dense(10, activation='softmax')(output)

    model = Model(inputs=[input], outputs=output)

    model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['acc'])

    return model

model_1 = build_model()
model_1.summary()

Model: "functional"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type)                         ┃ Output Shape                ┃         Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ input_layer (InputLayer)             │ (None, 28, 28, 1)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d (Conv2D)                      │ (None, 28, 28, 32)          │             320 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_1 (Conv2D)                    │ (None, 28, 28, 32)          │           9,248 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_2 (Conv2D)                    │ (None, 28, 28, 32)          │           9,248 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten (Flatten)                    │ (None, 25088)               │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense (Dense)                        │ (None, 128)                 │       3,211,392 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_1 (Dense)                      │ (None, 64)                  │           8,256 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_2 (Dense)                      │ (None, 10)                  │             650 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘

 Total params: 3,239,114 (12.36 MB)

 Trainable params: 3,239,114 (12.36 MB)

 Non-trainable params: 0 (0.00 B)

hist_1 = model_1.fit(x_train, y_train,
                     epochs=20,
                     validation_split=0.3,
                     batch_size=512)

Epoch 1/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 13s 68ms/step - acc: 0.6512 - loss: 0.9781 - val_acc: 0.8304 - val_loss: 0.4678
Epoch 2/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 30ms/step - acc: 0.8564 - loss: 0.3977 - val_acc: 0.8658 - val_loss: 0.3770
Epoch 3/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 31ms/step - acc: 0.8847 - loss: 0.3199 - val_acc: 0.8898 - val_loss: 0.3059
Epoch 4/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 30ms/step - acc: 0.9049 - loss: 0.2574 - val_acc: 0.8946 - val_loss: 0.2976
Epoch 5/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 5s 33ms/step - acc: 0.9172 - loss: 0.2230 - val_acc: 0.8961 - val_loss: 0.2930
Epoch 6/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 40ms/step - acc: 0.9273 - loss: 0.1986 - val_acc: 0.9093 - val_loss: 0.2612
Epoch 7/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 34ms/step - acc: 0.9399 - loss: 0.1639 - val_acc: 0.8875 - val_loss: 0.3520
Epoch 8/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 5s 29ms/step - acc: 0.9346 - loss: 0.1766 - val_acc: 0.8737 - val_loss: 0.3914
Epoch 9/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 28ms/step - acc: 0.9398 - loss: 0.1657 - val_acc: 0.9060 - val_loss: 0.2923
Epoch 10/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 28ms/step - acc: 0.9608 - loss: 0.1113 - val_acc: 0.9093 - val_loss: 0.2991
Epoch 11/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 29ms/step - acc: 0.9657 - loss: 0.0964 - val_acc: 0.9070 - val_loss: 0.3465
Epoch 12/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 29ms/step - acc: 0.9699 - loss: 0.0851 - val_acc: 0.9096 - val_loss: 0.3286
Epoch 13/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 28ms/step - acc: 0.9814 - loss: 0.0536 - val_acc: 0.9056 - val_loss: 0.3904
Epoch 14/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 28ms/step - acc: 0.9776 - loss: 0.0685 - val_acc: 0.9146 - val_loss: 0.3694
Epoch 15/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 28ms/step - acc: 0.9920 - loss: 0.0262 - val_acc: 0.9105 - val_loss: 0.4255
Epoch 16/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 29ms/step - acc: 0.9878 - loss: 0.0361 - val_acc: 0.9142 - val_loss: 0.4280
Epoch 17/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 29ms/step - acc: 0.9955 - loss: 0.0153 - val_acc: 0.9119 - val_loss: 0.4758
Epoch 18/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 28ms/step - acc: 0.9964 - loss: 0.0120 - val_acc: 0.9134 - val_loss: 0.4914
Epoch 19/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 28ms/step - acc: 0.9976 - loss: 0.0086 - val_acc: 0.9142 - val_loss: 0.5214
Epoch 20/20
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 28ms/step - acc: 0.9989 - loss: 0.0054 - val_acc: 0.9144 - val_loss: 0.5490

hist_1.history.keys()

plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
plt.plot(hist_1.history['loss'], 'b--', label='loss')
plt.plot(hist_1.history['val_loss'],'r:',label='val_loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.grid()
plt.legend()

plt.subplot(1,2,2)
plt.plot(hist_1.history['acc'], 'b--', label='acc')
plt.plot(hist_1.history['val_acc'],'r:',label='val_acc')
plt.xlabel('Epochs')
plt.ylabel('accuracy')
plt.grid()
plt.legend()
plt.show()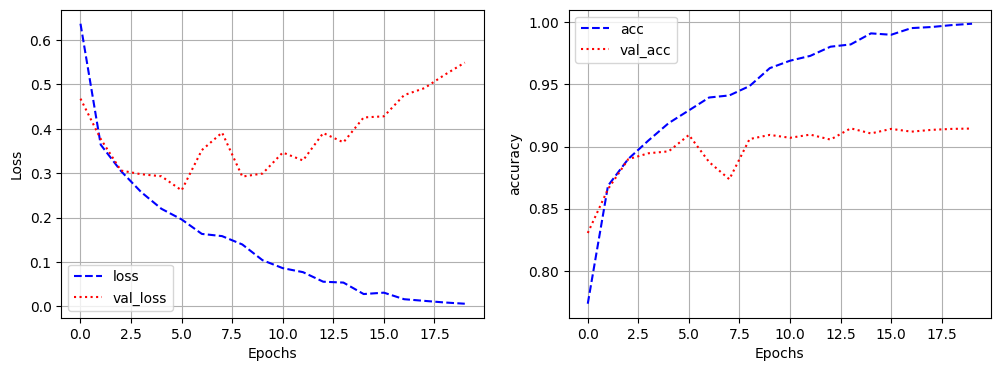

model_1.evaluate(x_test, y_test)

313/313 ━━━━━━━━━━━━━━━━━━━━ 2s 3ms/step - acc: 0.9092 - loss: 0.6197





[0.602406919002533, 0.9063000082969666]

모델 구성 및 학습: 과대적합 방지

• 학습 파라미터의 수 비교

def build_model2():
    # 입력 레이어 정의
    input = Input(shape=(28,28,1))

    output = Conv2D(filters=32, kernel_size=3, activation='relu', padding='same')(input)
    output = MaxPooling2D(strides=2)(output)

    output = Conv2D(filters=32, kernel_size=3, activation='relu', padding='same')(output)
    output = MaxPooling2D(strides=2)(output)
    output = Dropout(0.4)(output)

    output = Conv2D(filters=32, kernel_size=3, activation='relu', padding='same')(output)
    output = Dropout(0.4)(output)

    # 평탄화와 완전 연결 레이어
    output = Flatten()(output)
    output = Dense(128, activation='relu')(output)
    output = Dense(64, activation='relu')(output)

    # 출력 레이어
    output = Dense(10, activation='softmax')(output)

    model = Model(inputs=[input], outputs=output)

    model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['acc'])

    return model

model_2 = build_model2()
model_2.summary()

Model: "functional_3"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type)                         ┃ Output Shape                ┃         Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ input_layer_3 (InputLayer)           │ (None, 28, 28, 1)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_9 (Conv2D)                    │ (None, 28, 28, 32)          │             320 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_2 (MaxPooling2D)       │ (None, 14, 14, 32)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_10 (Conv2D)                   │ (None, 14, 14, 32)          │           9,248 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_3 (MaxPooling2D)       │ (None, 7, 7, 32)            │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_2 (Dropout)                  │ (None, 7, 7, 32)            │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_11 (Conv2D)                   │ (None, 7, 7, 32)            │           9,248 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_3 (Dropout)                  │ (None, 7, 7, 32)            │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten_3 (Flatten)                  │ (None, 1568)                │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_9 (Dense)                      │ (None, 128)                 │         200,832 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_10 (Dense)                     │ (None, 64)                  │           8,256 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_11 (Dense)                     │ (None, 10)                  │             650 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘

 Total params: 228,554 (892.79 KB)

 Trainable params: 228,554 (892.79 KB)

 Non-trainable params: 0 (0.00 B)

hist_2 = model_2.fit(x_train, y_train,
                     epochs=40,
                     validation_split=0.3,
                     batch_size=512)

Epoch 1/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 8s 59ms/step - acc: 0.5021 - loss: 1.4116 - val_acc: 0.7751 - val_loss: 0.5945
Epoch 2/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 4s 11ms/step - acc: 0.7724 - loss: 0.5961 - val_acc: 0.8313 - val_loss: 0.4664
Epoch 3/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.8223 - loss: 0.4867 - val_acc: 0.8351 - val_loss: 0.4346
Epoch 4/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - acc: 0.8314 - loss: 0.4567 - val_acc: 0.8628 - val_loss: 0.3815
Epoch 5/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.8552 - loss: 0.4041 - val_acc: 0.8757 - val_loss: 0.3460
Epoch 6/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 12ms/step - acc: 0.8554 - loss: 0.3948 - val_acc: 0.8814 - val_loss: 0.3294
Epoch 7/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 12ms/step - acc: 0.8701 - loss: 0.3554 - val_acc: 0.8718 - val_loss: 0.3508
Epoch 8/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - acc: 0.8619 - loss: 0.3682 - val_acc: 0.8886 - val_loss: 0.3064
Epoch 9/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - acc: 0.8746 - loss: 0.3418 - val_acc: 0.8887 - val_loss: 0.3051
Epoch 10/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.8773 - loss: 0.3354 - val_acc: 0.8958 - val_loss: 0.2841
Epoch 11/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - acc: 0.8832 - loss: 0.3175 - val_acc: 0.8904 - val_loss: 0.2967
Epoch 12/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.8809 - loss: 0.3196 - val_acc: 0.8974 - val_loss: 0.2780
Epoch 13/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - acc: 0.8830 - loss: 0.3095 - val_acc: 0.9017 - val_loss: 0.2681
Epoch 14/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 12ms/step - acc: 0.8900 - loss: 0.2956 - val_acc: 0.9008 - val_loss: 0.2671
Epoch 15/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.8896 - loss: 0.2998 - val_acc: 0.8984 - val_loss: 0.2735
Epoch 16/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.8942 - loss: 0.2825 - val_acc: 0.9066 - val_loss: 0.2590
Epoch 17/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.8918 - loss: 0.2820 - val_acc: 0.9088 - val_loss: 0.2516
Epoch 18/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - acc: 0.8960 - loss: 0.2823 - val_acc: 0.8995 - val_loss: 0.2668
Epoch 19/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 15ms/step - acc: 0.8983 - loss: 0.2699 - val_acc: 0.9087 - val_loss: 0.2475
Epoch 20/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 13ms/step - acc: 0.9016 - loss: 0.2681 - val_acc: 0.9141 - val_loss: 0.2390
Epoch 21/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9043 - loss: 0.2582 - val_acc: 0.9126 - val_loss: 0.2389
Epoch 22/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.8995 - loss: 0.2648 - val_acc: 0.9127 - val_loss: 0.2425
Epoch 23/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9019 - loss: 0.2676 - val_acc: 0.9166 - val_loss: 0.2280
Epoch 24/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9075 - loss: 0.2469 - val_acc: 0.9136 - val_loss: 0.2336
Epoch 25/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9107 - loss: 0.2395 - val_acc: 0.9155 - val_loss: 0.2313
Epoch 26/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9138 - loss: 0.2304 - val_acc: 0.9148 - val_loss: 0.2368
Epoch 27/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9100 - loss: 0.2364 - val_acc: 0.9172 - val_loss: 0.2285
Epoch 28/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - acc: 0.9080 - loss: 0.2471 - val_acc: 0.9198 - val_loss: 0.2229
Epoch 29/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - acc: 0.9121 - loss: 0.2334 - val_acc: 0.9174 - val_loss: 0.2269
Epoch 30/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 11ms/step - acc: 0.9122 - loss: 0.2322 - val_acc: 0.9189 - val_loss: 0.2228
Epoch 31/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9086 - loss: 0.2378 - val_acc: 0.9204 - val_loss: 0.2224
Epoch 32/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9131 - loss: 0.2292 - val_acc: 0.9209 - val_loss: 0.2198
Epoch 33/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 13ms/step - acc: 0.9154 - loss: 0.2256 - val_acc: 0.9201 - val_loss: 0.2189
Epoch 34/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 12ms/step - acc: 0.9153 - loss: 0.2237 - val_acc: 0.9161 - val_loss: 0.2290
Epoch 35/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - acc: 0.9155 - loss: 0.2244 - val_acc: 0.9221 - val_loss: 0.2133
Epoch 36/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9209 - loss: 0.2112 - val_acc: 0.9229 - val_loss: 0.2155
Epoch 37/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9238 - loss: 0.2039 - val_acc: 0.9199 - val_loss: 0.2152
Epoch 38/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9188 - loss: 0.2157 - val_acc: 0.9222 - val_loss: 0.2143
Epoch 39/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - acc: 0.9239 - loss: 0.2039 - val_acc: 0.9150 - val_loss: 0.2285
Epoch 40/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - acc: 0.9230 - loss: 0.2062 - val_acc: 0.9222 - val_loss: 0.2114

hist_2.history.keys()

plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
plt.plot(hist_2.history['loss'], 'b--', label='loss')
plt.plot(hist_2.history['val_loss'],'r:',label='val_loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.grid()
plt.legend()

plt.subplot(1,2,2)
plt.plot(hist_2.history['acc'], 'b--', label='acc')
plt.plot(hist_2.history['val_acc'],'r:',label='val_acc')
plt.xlabel('Epochs')
plt.ylabel('accuracy')
plt.grid()
plt.legend()
plt.show()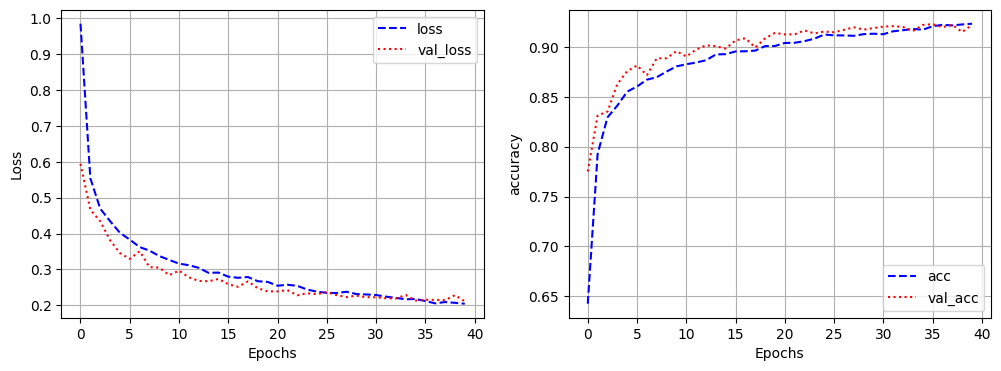

model_2.evaluate(x_test, y_test) # 학습시간 감소 및 과적합 방지

313/313 ━━━━━━━━━━━━━━━━━━━━ 2s 4ms/step - acc: 0.9150 - loss: 0.2314





[0.22845305502414703, 0.9151999950408936]

모델 성능 높이기: 레이어 추가

# 배치마다 층의 출력을 정규화하여 학습을 안정화하고 속도를 높이며, 과적합을 줄이는 효과
# 평균이 0, 표준편차가 1이 되도록 변형
from tensorflow.keras.layers import BatchNormalization

def build_model3():
    # 입력 레이어 정의
    input = Input(shape=(28,28,1))

    output = Conv2D(filters=32, kernel_size=3, activation='relu', padding='same')(input)
    output = BatchNormalization()(output)
    output = MaxPooling2D(strides=2)(output)

    output = Conv2D(filters=64, kernel_size=3, activation='relu', padding='valid')(output)
    output = BatchNormalization()(output)
    output = MaxPooling2D(strides=2)(output)
    output = Dropout(0.4)(output)

    output = Conv2D(filters=128, kernel_size=3, activation='relu', padding='same')(output)
    output = Dropout(0.4)(output)

    # 평탄화와 완전 연결 레이어
    output = Flatten()(output)
    output = Dense(512, activation='relu')(output)
    output = BatchNormalization()(output)
    output = Dense(256, activation='relu')(output)
    output = BatchNormalization()(output)

    # 출력 레이어
    output = Dense(10, activation='softmax')(output)

    model = Model(inputs=[input], outputs=output)

    model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['acc'])

    return model

model_3 = build_model3()
model_3.summary()

Model: "functional_5"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type)                         ┃ Output Shape                ┃         Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ input_layer_5 (InputLayer)           │ (None, 28, 28, 1)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_15 (Conv2D)                   │ (None, 28, 28, 32)          │             320 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_4                │ (None, 28, 28, 32)          │             128 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_6 (MaxPooling2D)       │ (None, 14, 14, 32)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_16 (Conv2D)                   │ (None, 12, 12, 64)          │          18,496 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_5                │ (None, 12, 12, 64)          │             256 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_7 (MaxPooling2D)       │ (None, 6, 6, 64)            │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_6 (Dropout)                  │ (None, 6, 6, 64)            │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_17 (Conv2D)                   │ (None, 6, 6, 128)           │          73,856 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_7 (Dropout)                  │ (None, 6, 6, 128)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten_5 (Flatten)                  │ (None, 4608)                │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_15 (Dense)                     │ (None, 512)                 │       2,359,808 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_6                │ (None, 512)                 │           2,048 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_16 (Dense)                     │ (None, 256)                 │         131,328 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_7                │ (None, 256)                 │           1,024 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_17 (Dense)                     │ (None, 10)                  │           2,570 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘

 Total params: 2,589,834 (9.88 MB)

 Trainable params: 2,588,106 (9.87 MB)

 Non-trainable params: 1,728 (6.75 KB)

hist_3 = model_3.fit(x_train, y_train,
                     epochs=40,
                     validation_split=0.3,
                     batch_size=512)

Epoch 1/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 21s 160ms/step - acc: 0.7350 - loss: 0.7634 - val_acc: 0.1299 - val_loss: 2.7767
Epoch 2/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - acc: 0.8582 - loss: 0.3842 - val_acc: 0.3571 - val_loss: 2.5578
Epoch 3/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 16ms/step - acc: 0.8845 - loss: 0.3142 - val_acc: 0.4129 - val_loss: 1.9564
Epoch 4/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.8887 - loss: 0.2980 - val_acc: 0.6051 - val_loss: 1.2800
Epoch 5/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 19ms/step - acc: 0.8991 - loss: 0.2685 - val_acc: 0.7246 - val_loss: 0.7777
Epoch 6/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 20ms/step - acc: 0.9092 - loss: 0.2384 - val_acc: 0.7784 - val_loss: 0.6222
Epoch 7/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9110 - loss: 0.2406 - val_acc: 0.8777 - val_loss: 0.3326
Epoch 8/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9180 - loss: 0.2145 - val_acc: 0.9142 - val_loss: 0.2361
Epoch 9/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - acc: 0.9120 - loss: 0.2314 - val_acc: 0.9153 - val_loss: 0.2320
Epoch 10/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9286 - loss: 0.1951 - val_acc: 0.9119 - val_loss: 0.2439
Epoch 11/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 19ms/step - acc: 0.9304 - loss: 0.1859 - val_acc: 0.9118 - val_loss: 0.2508
Epoch 12/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 23ms/step - acc: 0.9236 - loss: 0.2017 - val_acc: 0.8492 - val_loss: 0.4852
Epoch 13/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9318 - loss: 0.1800 - val_acc: 0.9248 - val_loss: 0.2186
Epoch 14/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9301 - loss: 0.1841 - val_acc: 0.9146 - val_loss: 0.2461
Epoch 15/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9372 - loss: 0.1692 - val_acc: 0.9279 - val_loss: 0.2054
Epoch 16/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 18ms/step - acc: 0.9417 - loss: 0.1566 - val_acc: 0.9127 - val_loss: 0.2526
Epoch 17/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 19ms/step - acc: 0.9340 - loss: 0.1773 - val_acc: 0.8458 - val_loss: 0.5771
Epoch 18/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 18ms/step - acc: 0.9166 - loss: 0.2161 - val_acc: 0.8932 - val_loss: 0.3014
Epoch 19/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - acc: 0.9365 - loss: 0.1630 - val_acc: 0.9253 - val_loss: 0.2123
Epoch 20/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9461 - loss: 0.1421 - val_acc: 0.9290 - val_loss: 0.2070
Epoch 21/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 19ms/step - acc: 0.9450 - loss: 0.1443 - val_acc: 0.9127 - val_loss: 0.2592
Epoch 22/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 19ms/step - acc: 0.9522 - loss: 0.1256 - val_acc: 0.9237 - val_loss: 0.2341
Epoch 23/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 18ms/step - acc: 0.9516 - loss: 0.1296 - val_acc: 0.9283 - val_loss: 0.2085
Epoch 24/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 19ms/step - acc: 0.9526 - loss: 0.1224 - val_acc: 0.9123 - val_loss: 0.2683
Epoch 25/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 20ms/step - acc: 0.9501 - loss: 0.1317 - val_acc: 0.9276 - val_loss: 0.2233
Epoch 26/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - acc: 0.9536 - loss: 0.1240 - val_acc: 0.9330 - val_loss: 0.2050
Epoch 27/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - acc: 0.9594 - loss: 0.1083 - val_acc: 0.9297 - val_loss: 0.2211
Epoch 28/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - acc: 0.9623 - loss: 0.1014 - val_acc: 0.9193 - val_loss: 0.2532
Epoch 29/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9594 - loss: 0.1092 - val_acc: 0.9223 - val_loss: 0.2487
Epoch 30/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 19ms/step - acc: 0.9532 - loss: 0.1246 - val_acc: 0.9099 - val_loss: 0.2844
Epoch 31/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 20ms/step - acc: 0.9551 - loss: 0.1161 - val_acc: 0.9290 - val_loss: 0.2255
Epoch 32/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - acc: 0.9599 - loss: 0.1057 - val_acc: 0.9151 - val_loss: 0.2691
Epoch 33/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 19ms/step - acc: 0.9633 - loss: 0.0979 - val_acc: 0.9321 - val_loss: 0.2323
Epoch 34/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9697 - loss: 0.0833 - val_acc: 0.9201 - val_loss: 0.2688
Epoch 35/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - acc: 0.9483 - loss: 0.1393 - val_acc: 0.9292 - val_loss: 0.2192
Epoch 36/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 19ms/step - acc: 0.9514 - loss: 0.1292 - val_acc: 0.9185 - val_loss: 0.2540
Epoch 37/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 18ms/step - acc: 0.9528 - loss: 0.1289 - val_acc: 0.9311 - val_loss: 0.2254
Epoch 38/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 2s 18ms/step - acc: 0.9658 - loss: 0.0902 - val_acc: 0.9335 - val_loss: 0.2218
Epoch 39/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 3s 19ms/step - acc: 0.9708 - loss: 0.0772 - val_acc: 0.9358 - val_loss: 0.2119
Epoch 40/40
83/83 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - acc: 0.9703 - loss: 0.0761 - val_acc: 0.9302 - val_loss: 0.2325

hist_3.history.keys()

plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
plt.plot(hist_3.history['loss'], 'b--', label='loss')
plt.plot(hist_3.history['val_loss'],'r:',label='val_loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.grid()
plt.legend()

plt.subplot(1,2,2)
plt.plot(hist_3.history['acc'], 'b--', label='acc')
plt.plot(hist_3.history['val_acc'],'r:',label='val_acc')
plt.xlabel('Epochs')
plt.ylabel('accuracy')
plt.grid()
plt.legend()
plt.show()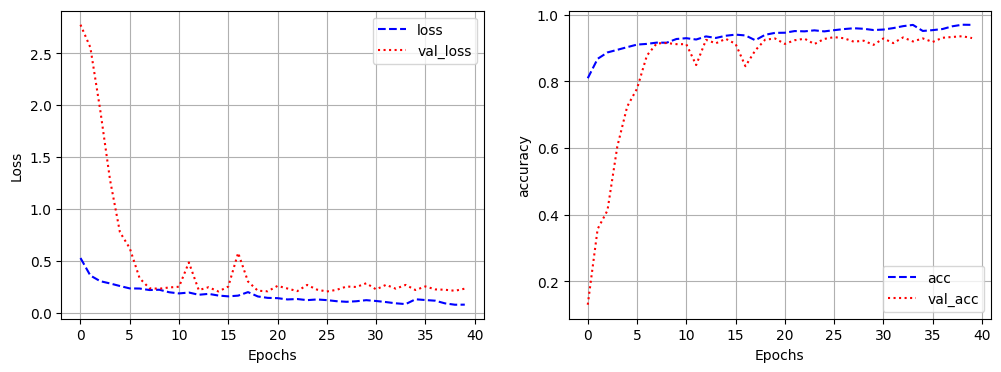

model_3.evaluate(x_test, y_test) # 학습시간 감소 및 과적합 방지

313/313 ━━━━━━━━━━━━━━━━━━━━ 2s 3ms/step - acc: 0.9212 - loss: 0.2699





[0.2635417580604553, 0.9228000044822693]

• 과대적합은 되지 않았고, 층을 늘려도 좋은 성능을 낼 수 있음

모델 성능 높이기: 이미지 보강(Image Augmentation)

• 주요 인자 참고: https://keras.io/ko/preprocessing/image/

from tensorflow.keras.preprocessing.image import ImageDataGenerator

image_generator = ImageDataGenerator(
    rotation_range=10,         # 이미지를 무작위로 최대 10도까지 회전
    zoom_range=0.2,            # 이미지를 무작위로 최대 20%까지 확대 또는 축소
    shear_range=0.7,           # 이미지를 무작위로 최대 0.7 라디안만큼 시프트
    width_shift_range=0.1,     # 이미지를 좌우로 최대 10%까지 이동
    height_shift_range=0.1,    # 이미지를 상하로 최대 10%까지 이동
    horizontal_flip=True,      # 이미지를 좌우로 무작위로 뒤집음
    vertical_flip=False        # 이미지를 상하로 뒤집지 않음
)

augment_size = 200
print(x_train.shape)
print(x_train[0].shape)

(60000, 28, 28, 1)
(28, 28, 1)

x_augment = image_generator.flow(
    x_train[:augment_size],
    batch_size=augment_size, # 한 번에 200개 이미지를 반환
    shuffle=False # 데이터를 무작위로 섞지 않고 원래 순서를 유지
    )

# 1개 이미지에 대한 증강 예시
# 여러 이미지로 할거면 x_augment[0][i]로 수정
plt.figure(figsize=(10,10))
for i in range(1,11):
    plt.subplot(1,10,i)
    plt.imshow(x_augment[0][0], cmap='gray')
    plt.axis('off')
plt.show()

데이터 추가

image_generator = ImageDataGenerator(
    rotation_range=15,         # 이미지를 무작위로 최대 10도까지 회전
    zoom_range=0.1,            # 이미지를 무작위로 최대 20%까지 확대 또는 축소
    shear_range=0.6,           # 이미지를 무작위로 최대 0.7 라디안만큼 시프트
    width_shift_range=0.1,     # 이미지를 좌우로 최대 10%까지 이동
    height_shift_range=0.1,    # 이미지를 상하로 최대 10%까지 이동
    horizontal_flip=True,      # 이미지를 좌우로 무작위로 뒤집음
    vertical_flip=False        # 이미지를 상하로 뒤집지 않음
)

augment_size = 20000

# x_train에서 10000개 샘플을 무작위로 선택
indices = np.random.permutation(len(x_train))[:20000]
x_sample = x_train[indices]

x_augmented = image_generator.flow(
    x_sample,           # 증강할 데이터 샘플
    batch_size=augment_size,  # 배치 크기: 한 번에 20000개 이미지 반환
    shuffle=False       # 데이터를 섞지 않고 원래 순서대로 반환
)

x_augmented = next(x_augmented)
y_augmented = y_train[indices]

x_train = np.concatenate((x_train, x_augmented))
y_train = np.concatenate((y_train, y_augmented))

print(x_train.shape)
print(y_train.shape)

(90000, 28, 28, 1)
(90000,)

x_augmented = image_generator.flow(
    x_sample[:1000],           # 증강할 데이터 샘플
    batch_size=10,  # 배치 크기: 한 번에 20000개 이미지 반환
    shuffle=False       # 데이터를 섞지 않고 원래 순서대로 반환
)
x_augmented = next(x_augmented)
x_augmented.shape

(10, 28, 28, 1)

model_4 = build_model3()
model_4.summary()

Model: "functional"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type)                         ┃ Output Shape                ┃         Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ input_layer_1 (InputLayer)           │ (None, 28, 28, 1)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_1 (Conv2D)                    │ (None, 28, 28, 32)          │             320 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization                  │ (None, 28, 28, 32)          │             128 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d (MaxPooling2D)         │ (None, 14, 14, 32)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_2 (Conv2D)                    │ (None, 12, 12, 64)          │          18,496 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_1                │ (None, 12, 12, 64)          │             256 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_1 (MaxPooling2D)       │ (None, 6, 6, 64)            │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout (Dropout)                    │ (None, 6, 6, 64)            │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_3 (Conv2D)                    │ (None, 6, 6, 128)           │          73,856 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_1 (Dropout)                  │ (None, 6, 6, 128)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten (Flatten)                    │ (None, 4608)                │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense (Dense)                        │ (None, 512)                 │       2,359,808 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_2                │ (None, 512)                 │           2,048 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_1 (Dense)                      │ (None, 256)                 │         131,328 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_3                │ (None, 256)                 │           1,024 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_2 (Dense)                      │ (None, 10)                  │           2,570 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘

 Total params: 2,589,834 (9.88 MB)

 Trainable params: 2,588,106 (9.87 MB)

 Non-trainable params: 1,728 (6.75 KB)

hist_4 = model_4.fit(x_train, y_train,
                     epochs=40,
                     validation_split=0.3,
                     batch_size=512)

Epoch 1/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 34s 184ms/step - acc: 0.7523 - loss: 0.7219 - val_acc: 0.0992 - val_loss: 3.1442
Epoch 2/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 13s 18ms/step - acc: 0.8723 - loss: 0.3486 - val_acc: 0.2008 - val_loss: 2.4828
Epoch 3/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.8899 - loss: 0.2960 - val_acc: 0.3189 - val_loss: 1.9961
Epoch 4/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.8967 - loss: 0.2757 - val_acc: 0.6415 - val_loss: 0.9980
Epoch 5/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9052 - loss: 0.2499 - val_acc: 0.7106 - val_loss: 0.8654
Epoch 6/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.9090 - loss: 0.2404 - val_acc: 0.7913 - val_loss: 0.5495
Epoch 7/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9149 - loss: 0.2268 - val_acc: 0.7949 - val_loss: 0.5521
Epoch 8/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.9221 - loss: 0.2066 - val_acc: 0.8007 - val_loss: 0.5301
Epoch 9/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 16ms/step - acc: 0.9266 - loss: 0.1929 - val_acc: 0.8075 - val_loss: 0.5180
Epoch 10/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 18ms/step - acc: 0.9203 - loss: 0.2103 - val_acc: 0.7842 - val_loss: 0.6006
Epoch 11/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 27ms/step - acc: 0.9272 - loss: 0.1967 - val_acc: 0.7857 - val_loss: 0.5904
Epoch 12/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 4s 18ms/step - acc: 0.9290 - loss: 0.1888 - val_acc: 0.7979 - val_loss: 0.5497
Epoch 13/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9324 - loss: 0.1761 - val_acc: 0.8160 - val_loss: 0.5017
Epoch 14/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9391 - loss: 0.1584 - val_acc: 0.8068 - val_loss: 0.5432
Epoch 15/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9387 - loss: 0.1629 - val_acc: 0.7942 - val_loss: 0.5781
Epoch 16/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9389 - loss: 0.1612 - val_acc: 0.7939 - val_loss: 0.5850
Epoch 17/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9422 - loss: 0.1505 - val_acc: 0.7552 - val_loss: 0.7547
Epoch 18/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.9452 - loss: 0.1445 - val_acc: 0.7646 - val_loss: 0.6880
Epoch 19/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.9440 - loss: 0.1467 - val_acc: 0.7863 - val_loss: 0.6695
Epoch 20/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 18ms/step - acc: 0.9511 - loss: 0.1321 - val_acc: 0.8042 - val_loss: 0.5792
Epoch 21/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 18ms/step - acc: 0.9557 - loss: 0.1169 - val_acc: 0.8122 - val_loss: 0.5416
Epoch 22/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.9530 - loss: 0.1261 - val_acc: 0.8137 - val_loss: 0.5474
Epoch 23/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9564 - loss: 0.1176 - val_acc: 0.8146 - val_loss: 0.5623
Epoch 24/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 16ms/step - acc: 0.9588 - loss: 0.1094 - val_acc: 0.8151 - val_loss: 0.5554
Epoch 25/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 18ms/step - acc: 0.9576 - loss: 0.1109 - val_acc: 0.7866 - val_loss: 0.7532
Epoch 26/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9547 - loss: 0.1175 - val_acc: 0.7893 - val_loss: 0.7020
Epoch 27/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.9541 - loss: 0.1183 - val_acc: 0.8107 - val_loss: 0.5805
Epoch 28/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.9624 - loss: 0.0984 - val_acc: 0.8139 - val_loss: 0.5872
Epoch 29/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9615 - loss: 0.0991 - val_acc: 0.8057 - val_loss: 0.6517
Epoch 30/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9671 - loss: 0.0884 - val_acc: 0.8136 - val_loss: 0.6044
Epoch 31/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 18ms/step - acc: 0.9662 - loss: 0.0898 - val_acc: 0.7320 - val_loss: 1.0154
Epoch 32/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9406 - loss: 0.1630 - val_acc: 0.8024 - val_loss: 0.6433
Epoch 33/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9539 - loss: 0.1209 - val_acc: 0.7805 - val_loss: 0.7357
Epoch 34/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9554 - loss: 0.1195 - val_acc: 0.8030 - val_loss: 0.6776
Epoch 35/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.9591 - loss: 0.1081 - val_acc: 0.8242 - val_loss: 0.5672
Epoch 36/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - acc: 0.9648 - loss: 0.0918 - val_acc: 0.8075 - val_loss: 0.6650
Epoch 37/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9717 - loss: 0.0742 - val_acc: 0.8067 - val_loss: 0.6721
Epoch 38/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 3s 16ms/step - acc: 0.9686 - loss: 0.0815 - val_acc: 0.8218 - val_loss: 0.5832
Epoch 39/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 17ms/step - acc: 0.9724 - loss: 0.0747 - val_acc: 0.8110 - val_loss: 0.7081
Epoch 40/40
124/124 ━━━━━━━━━━━━━━━━━━━━ 2s 16ms/step - acc: 0.9747 - loss: 0.0675 - val_acc: 0.7956 - val_loss: 0.7368

• 학습 인자를 이전과 다르게 주면서 학습하면 더 잘 나올것으로 판단

hist_4.history.keys()

plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
plt.plot(hist_4.history['loss'], 'b--', label='loss')
plt.plot(hist_4.history['val_loss'],'r:',label='val_loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.grid()
plt.legend()

plt.subplot(1,2,2)
plt.plot(hist_4.history['acc'], 'b--', label='acc')
plt.plot(hist_4.history['val_acc'],'r:',label='val_acc')
plt.xlabel('Epochs')
plt.ylabel('accuracy')
plt.grid()
plt.legend()
plt.show()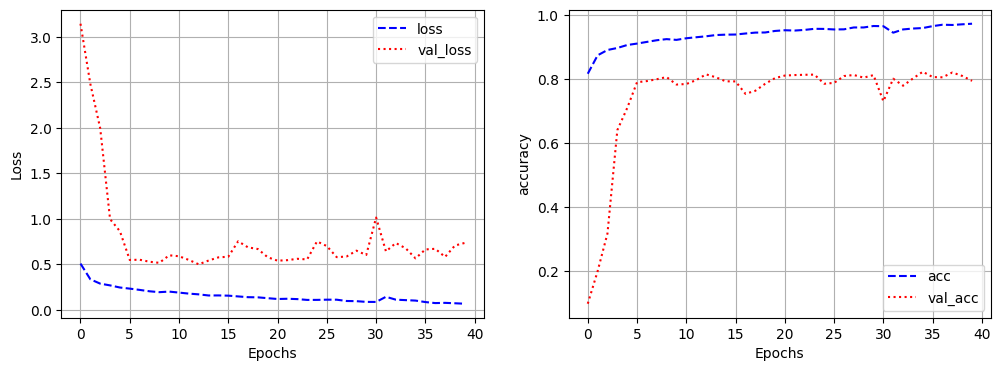

model_4.evaluate(x_test, y_test) # 학습시간 감소 및 과적합 방지

313/313 ━━━━━━━━━━━━━━━━━━━━ 3s 5ms/step - acc: 0.9187 - loss: 0.2915





[0.28360623121261597, 0.9200999736785889]

CIFAR-10

• CIFAR-10
  • 10개의 클래스로 구분된 32 x 32 사물 사진을 모은 데이터셋
  • 50,000개의 학습데이터, 10,000개의 테스트 데이터로 구성
  • 데이터 복잡도가 MNIST보다 훨씬 높은 특징이 있음
    • 단순한 신경망으로 특징을 검출하기 어려움

모듈 임포트

from tensorflow.keras.datasets import cifar10
from tensorflow.keras.layers import Conv2D, MaxPool2D, Dense, Input, Dropout, BatchNormalization
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.optimizers import Adam, SGD
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.utils import to_categorical

from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt

데이터 로드 및 전처리

(x_train_full, y_train_full), (x_test, y_test) = cifar10.load_data()

print(x_train_full.shape)
print(y_train_full.shape)
print(x_test.shape)
print(y_test.shape)

(50000, 32, 32, 3)
(50000, 1)
(10000, 32, 32, 3)
(10000, 1)

class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']

import random
plt.figure(figsize=(10, 5))
for i in range(10):
    plt.subplot(2, 5, i+1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    idx = random.randint(1,50000)
    plt.imshow(x_train_full[idx])
    plt.xlabel(class_names[y_train_full[idx][0]])

# x_train_full 데이터셋의 각 채널에 대한 평균을 계산
x_mean = np.mean(x_train_full, axis=(0,1,2)) # array([125.30691805, 122.95039414, 113.86538318])
# x_train_full 데이터셋의 각 채널에 대한 표준편차를 계산
x_std = np.std(x_train_full, axis=(0,1,2))

# 훈련 데이터를 정규화: 각 픽셀의 값에서 채널별 평균을 빼고, 채널별 표준편차로 나누어줍니다.
# 이 과정은 데이터의 평균을 0, 표준편차를 1로 맞추어줌으로써, 데이터를 정규화합니다. 이렇게 하면 모델이 더 빠르고 효율적으로 학습할 수 있습니다.
x_train_full = (x_train_full - x_mean) / x_std
x_test = (x_test - x_mean) / x_std

x_train, x_val, y_train, y_val = train_test_split(x_train_full, y_train_full,test_size = 0.2)

print(x_train.shape)
print(y_train.shape)

print(x_val.shape)
print(y_val.shape)

print(x_test.shape)
print(y_test.shape)

(40000, 32, 32, 3)
(40000, 1)
(10000, 32, 32, 3)
(10000, 1)
(10000, 32, 32, 3)
(10000, 1)

모델 구성 및 학습

def model_build():
    input = Input(shape=(32,32,3))

    output = Conv2D(filters=32, kernel_size=3, padding='same', activation='relu')(input)
    output = BatchNormalization()(output)
    output = MaxPool2D(pool_size=2, strides=2, padding='same')(output)
    output = Dropout(0.3)(output)  # Dropout 추가

    output = Conv2D(filters=64, kernel_size=3, padding='same', activation='relu')(output)
    output = BatchNormalization()(output)
    output = MaxPool2D(pool_size=2, strides=2, padding='same')(output)
    output = Dropout(0.3)(output)  # Dropout 추가

    output = Conv2D(filters=128, kernel_size=3, padding='same', activation='relu')(output)
    output = BatchNormalization()(output)
    output = MaxPool2D(pool_size=2, strides=2, padding='same')(output)
    output = Dropout(0.3)(output)  # Dropout 추가

    output = Flatten()(output)
    output = Dense(256, activation='relu')(output)
    output = Dense(128, activation='relu')(output)
    output = Dense(10, activation='softmax')(output)

    model = Model(inputs=input, outputs=output)

    model.compile(optimizer=Adam(learning_rate=1e-4),
                  loss='sparse_categorical_crossentropy',
                  metrics=['accuracy'])
    return model

model = model_build()
model.summary()

Model: "functional_2"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type)                         ┃ Output Shape                ┃         Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ input_layer_3 (InputLayer)           │ (None, 32, 32, 3)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_7 (Conv2D)                    │ (None, 32, 32, 32)          │             896 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_4                │ (None, 32, 32, 32)          │             128 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_5 (MaxPooling2D)       │ (None, 16, 16, 32)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_2 (Dropout)                  │ (None, 16, 16, 32)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_8 (Conv2D)                    │ (None, 16, 16, 64)          │          18,496 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_5                │ (None, 16, 16, 64)          │             256 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_6 (MaxPooling2D)       │ (None, 8, 8, 64)            │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_3 (Dropout)                  │ (None, 8, 8, 64)            │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_9 (Conv2D)                    │ (None, 8, 8, 128)           │          73,856 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_6                │ (None, 8, 8, 128)           │             512 │
│ (BatchNormalization)                 │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_7 (MaxPooling2D)       │ (None, 4, 4, 128)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_4 (Dropout)                  │ (None, 4, 4, 128)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten_2 (Flatten)                  │ (None, 2048)                │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_6 (Dense)                      │ (None, 256)                 │         524,544 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_7 (Dense)                      │ (None, 128)                 │          32,896 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_8 (Dense)                      │ (None, 10)                  │           1,290 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘

 Total params: 652,874 (2.49 MB)

 Trainable params: 652,426 (2.49 MB)

 Non-trainable params: 448 (1.75 KB)

history = model.fit(x_train, y_train,
                    epochs=30,
                    batch_size=256,
                    validation_data=(x_val, y_val),
                    verbose=1)

Epoch 1/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 14s 45ms/step - accuracy: 0.2141 - loss: 2.3805 - val_accuracy: 0.1080 - val_loss: 2.6461
Epoch 2/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.3799 - loss: 1.7169 - val_accuracy: 0.2475 - val_loss: 2.1843
Epoch 3/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 13ms/step - accuracy: 0.4375 - loss: 1.5589 - val_accuracy: 0.3796 - val_loss: 1.7988
Epoch 4/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 15ms/step - accuracy: 0.4722 - loss: 1.4586 - val_accuracy: 0.4345 - val_loss: 1.6436
Epoch 5/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.5085 - loss: 1.3641 - val_accuracy: 0.4518 - val_loss: 1.6275
Epoch 6/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 14ms/step - accuracy: 0.5273 - loss: 1.3022 - val_accuracy: 0.4682 - val_loss: 1.5677
Epoch 7/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.5494 - loss: 1.2620 - val_accuracy: 0.4836 - val_loss: 1.5374
Epoch 8/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.5694 - loss: 1.2036 - val_accuracy: 0.4937 - val_loss: 1.5278
Epoch 9/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 14ms/step - accuracy: 0.5831 - loss: 1.1606 - val_accuracy: 0.5038 - val_loss: 1.5092
Epoch 10/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.5991 - loss: 1.1246 - val_accuracy: 0.5139 - val_loss: 1.4902
Epoch 11/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.6068 - loss: 1.0984 - val_accuracy: 0.5207 - val_loss: 1.4868
Epoch 12/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 12ms/step - accuracy: 0.6163 - loss: 1.0636 - val_accuracy: 0.5354 - val_loss: 1.4020
Epoch 13/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 13ms/step - accuracy: 0.6294 - loss: 1.0313 - val_accuracy: 0.5522 - val_loss: 1.3588
Epoch 14/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 14ms/step - accuracy: 0.6372 - loss: 1.0137 - val_accuracy: 0.5594 - val_loss: 1.3492
Epoch 15/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.6482 - loss: 0.9896 - val_accuracy: 0.5594 - val_loss: 1.3671
Epoch 16/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.6594 - loss: 0.9630 - val_accuracy: 0.5738 - val_loss: 1.2931
Epoch 17/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 12ms/step - accuracy: 0.6688 - loss: 0.9328 - val_accuracy: 0.5773 - val_loss: 1.2941
Epoch 18/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 12ms/step - accuracy: 0.6717 - loss: 0.9184 - val_accuracy: 0.5790 - val_loss: 1.2898
Epoch 19/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 13ms/step - accuracy: 0.6817 - loss: 0.8892 - val_accuracy: 0.5928 - val_loss: 1.2357
Epoch 20/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 14ms/step - accuracy: 0.6863 - loss: 0.8761 - val_accuracy: 0.6040 - val_loss: 1.2148
Epoch 21/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 14ms/step - accuracy: 0.6956 - loss: 0.8556 - val_accuracy: 0.6048 - val_loss: 1.1849
Epoch 22/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.7016 - loss: 0.8328 - val_accuracy: 0.6123 - val_loss: 1.1645
Epoch 23/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.7058 - loss: 0.8243 - val_accuracy: 0.6244 - val_loss: 1.1196
Epoch 24/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.7149 - loss: 0.8032 - val_accuracy: 0.6439 - val_loss: 1.0559
Epoch 25/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.7195 - loss: 0.7888 - val_accuracy: 0.6500 - val_loss: 1.0487
Epoch 26/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 14ms/step - accuracy: 0.7284 - loss: 0.7690 - val_accuracy: 0.6487 - val_loss: 1.0579
Epoch 27/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.7336 - loss: 0.7528 - val_accuracy: 0.6521 - val_loss: 1.0606
Epoch 28/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 12ms/step - accuracy: 0.7393 - loss: 0.7347 - val_accuracy: 0.6640 - val_loss: 1.0194
Epoch 29/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.7464 - loss: 0.7170 - val_accuracy: 0.6682 - val_loss: 1.0068
Epoch 30/30
157/157 ━━━━━━━━━━━━━━━━━━━━ 3s 12ms/step - accuracy: 0.7474 - loss: 0.7082 - val_accuracy: 0.6692 - val_loss: 1.0084

plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
plt.plot(history.history['loss'], 'b--', label='loss')
plt.plot(history.history['val_loss'],'r:',label='val_loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.grid()
plt.legend()

plt.subplot(1,2,2)
plt.plot(history.history['accuracy'], 'b--', label='acc')
plt.plot(history.history['val_accuracy'],'r:',label='val_acc')
plt.xlabel('Epochs')
plt.ylabel('accuracy')
plt.grid()
plt.legend()
plt.show()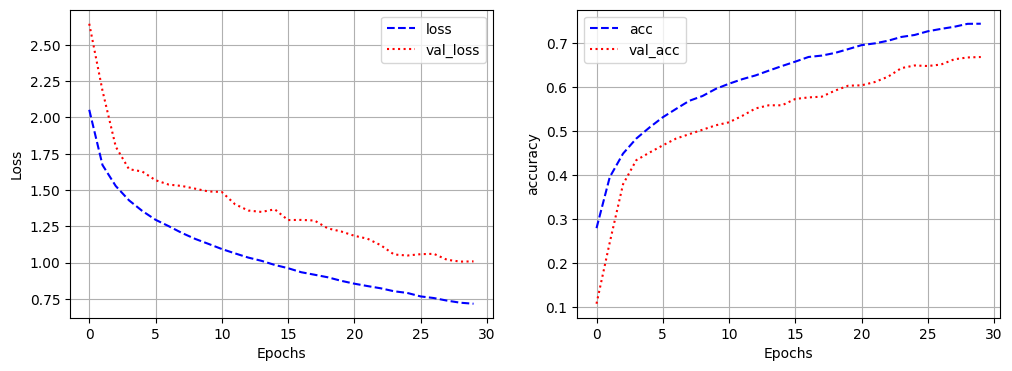

CNN 모델의 발전

• 1998: LeNet – Gradient-based Learning Applied to Document Recognition
• 2012: AlexNet – ImageNet Classification with Deep Convolutional Neural Network
• 2014: VggNet – Very Deep Convolutional Networks for Large-Scale Image Recognition
• 2014: GooLeNet – Going Deeper with Convolutions
• 2014: SppNet – Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition
• 2015: ResNet – Deep Residual Learning for Image Recognition
• 2016: Xception – Xception: Deep Learning with Depthwise Separable Convolutions
• 2017: MobileNet – MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Application
• 2017: DenseNet – Densely Connected Convolutional Networks
• 2017: SeNet – Squeeze and Excitation Networks
• 2017: ShuffleNet – ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
• 2018: NasNet – Learning Transferable Architectures for Scalable Image Recognition
• 2018: Bag of Tricks – Bag of Tricks for Image Classification with Convolutional Neural Networks
• 2019: EfficientNet – EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks

VGGNet(Visual Geometry Group Net)

• 2014년 ILSVRC에서 2등 차지 (상위-5 오류율: 7.32%), 이 후의 수많은 연구에 영향을 미침

• ImageNet에서 훈련이 끝난 후 얻게된 매개변수 값 로딩
• 네트워크를 다시 처음부터 학습하고자 한다면 weights=None으로 설정, 케라스에서 무작위로 가중치를 설정함
• include_top=False: VGG의 밀집 계층을 제외한다는 뜻
• 해당 네트워크의 출력은 합성곱/최대-풀링 블록의 특징맵이 됨
• pooling: 특징맵을 반환하기 전에 적용할 선택적인 연산을 지정

from keras.preprocessing import image
from keras.applications.vgg19 import VGG19, preprocess_input, decode_predictions

vggnet = VGG19(
    include_top=True,         # 최상위(fully connected) 분류 레이어를 포함할지 여부, True면 ImageNet 클래스 분류가 가능
    weights='imagenet',       # 사전 학습된 ImageNet 가중치 사용
    input_tensor=None,        # 입력 텐서를 지정할 경우, 기본값 None
    input_shape=None,         # 입력 이미지의 크기를 지정하지 않으면 기본값 사용 (224x224x3)
    pooling=None,             # 완전 연결 레이어 대신 특정 pooling을 할지 설정 가능 (None이면 기본 사용)
    classes=1000              # ImageNet의 클래스 개수 (1,000개)
    )
vggnet.summary()

Downloading data from https://storage.googleapis.com/tensorflow/keras-applications/vgg19/vgg19_weights_tf_dim_ordering_tf_kernels.h5
574710816/574710816 ━━━━━━━━━━━━━━━━━━━━ 12s 0us/step

Model: "vgg19"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type)                         ┃ Output Shape                ┃         Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ input_layer_4 (InputLayer)           │ (None, 224, 224, 3)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block1_conv1 (Conv2D)                │ (None, 224, 224, 64)        │           1,792 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block1_conv2 (Conv2D)                │ (None, 224, 224, 64)        │          36,928 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block1_pool (MaxPooling2D)           │ (None, 112, 112, 64)        │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block2_conv1 (Conv2D)                │ (None, 112, 112, 128)       │          73,856 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block2_conv2 (Conv2D)                │ (None, 112, 112, 128)       │         147,584 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block2_pool (MaxPooling2D)           │ (None, 56, 56, 128)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block3_conv1 (Conv2D)                │ (None, 56, 56, 256)         │         295,168 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block3_conv2 (Conv2D)                │ (None, 56, 56, 256)         │         590,080 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block3_conv3 (Conv2D)                │ (None, 56, 56, 256)         │         590,080 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block3_conv4 (Conv2D)                │ (None, 56, 56, 256)         │         590,080 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block3_pool (MaxPooling2D)           │ (None, 28, 28, 256)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block4_conv1 (Conv2D)                │ (None, 28, 28, 512)         │       1,180,160 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block4_conv2 (Conv2D)                │ (None, 28, 28, 512)         │       2,359,808 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block4_conv3 (Conv2D)                │ (None, 28, 28, 512)         │       2,359,808 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block4_conv4 (Conv2D)                │ (None, 28, 28, 512)         │       2,359,808 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block4_pool (MaxPooling2D)           │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block5_conv1 (Conv2D)                │ (None, 14, 14, 512)         │       2,359,808 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block5_conv2 (Conv2D)                │ (None, 14, 14, 512)         │       2,359,808 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block5_conv3 (Conv2D)                │ (None, 14, 14, 512)         │       2,359,808 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block5_conv4 (Conv2D)                │ (None, 14, 14, 512)         │       2,359,808 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ block5_pool (MaxPooling2D)           │ (None, 7, 7, 512)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten (Flatten)                    │ (None, 25088)               │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ fc1 (Dense)                          │ (None, 4096)                │     102,764,544 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ fc2 (Dense)                          │ (None, 4096)                │      16,781,312 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ predictions (Dense)                  │ (None, 1000)                │       4,097,000 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘

 Total params: 143,667,240 (548.05 MB)

 Trainable params: 143,667,240 (548.05 MB)

 Non-trainable params: 0 (0.00 B)

• dog.jpg (https://www.publicdomainpictures.net/pictures/250000/nahled/dog-beagle-portrait.jpg)

!wget -O dog.jpg https://www.publicdomainpictures.net/pictures/250000/nahled/dog-beagle-portrait.jpg

--2024-11-07 08:18:31--  https://www.publicdomainpictures.net/pictures/250000/nahled/dog-beagle-portrait.jpg
Resolving www.publicdomainpictures.net (www.publicdomainpictures.net)... 104.20.122.60, 104.20.123.60, 172.67.1.236, ...
Connecting to www.publicdomainpictures.net (www.publicdomainpictures.net)|104.20.122.60|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 88498 (86K) [image/jpeg]
Saving to: ‘dog.jpg’

dog.jpg             100%[===================>]  86.42K  --.-KB/s    in 0.02s   

2024-11-07 08:18:31 (5.28 MB/s) - ‘dog.jpg’ saved [88498/88498]

img = image.load_img('dog.jpg', target_size=(224, 224))
plt.imshow(img)

x = image.img_to_array(img)
x = preprocess_input(np.expand_dims(x,0))

preds = vggnet.predict(x)
print(decode_predictions(preds))

1/1 ━━━━━━━━━━━━━━━━━━━━ 3s 3s/step
Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/imagenet_class_index.json
35363/35363 ━━━━━━━━━━━━━━━━━━━━ 0s 0us/step
[[('n02088364', 'beagle', 0.83840275), ('n02089973', 'English_foxhound', 0.08918254), ('n02089867', 'Walker_hound', 0.0624161), ('n02088238', 'basset', 0.0046146614), ('n02088632', 'bluetick', 0.003374971)]]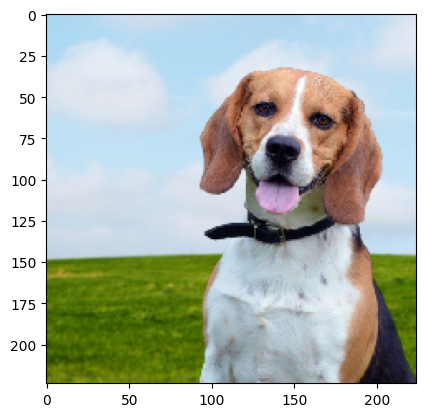

GoogLeNet, Inception

• VGGNet을 제치고 같은 해 분류 과제에서 1등을 차지

• 인셉션 블록이라는 개념을 도입하여, 인셉션 네트워크(Inception Network)라고도 불림

• 깊고 넓은 네트워크 구조를 가지면서도 효율적인 연산 구조를 가지고 있음

  

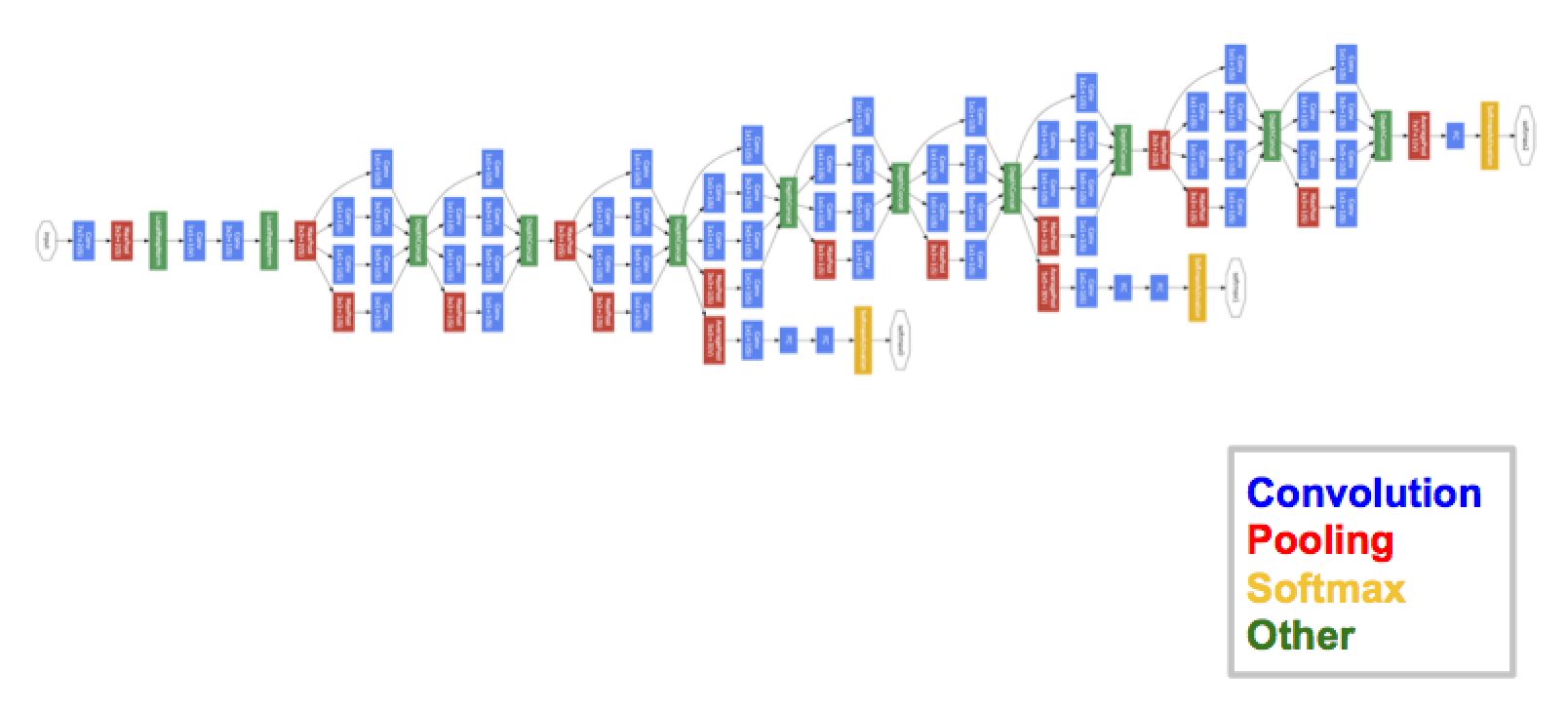
• 특징

  • GoogLeNet은 CNN 모델의 계산량을 최적화하는 데 중점을 둠
  • 초기에는 전형적인 합성곱 계층과 풀링 계층으로 시작하며, 이후에 이 정보는 9개의 인셉션 모듈(Inception Module) 스택을 통과
  • 인셉션 모듈에서는 입력 특징 맵이 서로 다른 기능을 수행하는 4개의 병렬 하위 블록으로 전달. 이 하위 블록들은 서로 다른 커널 크기와 풀링 방식을 사용하여 다양한 특징을 추출하고, 다시 연결하여 다음 계층으로 전달
  • 모든 합성곱 및 풀링 계층에는 'SAME' 패딩과 stride=1 설정이 적용. 활성화 함수로는 ReLU가 사용되어 모델의 비선형성을 부여

• 기여

  • 블록과 병목 구조를 통해 연산량을 효율적으로 관리하고, 네트워크가 더 깊어지면서도 학습에 안정성을 부여할 수 있게 함
  • 병목 계층으로 1x1 합성곱 계층 사용(채널 수를 줄여 연산량 감소)
  • 병목 계층은 중요한 정보만을 추출하고 압축하여 다음 계층으로 전달할 수 있음. 이를 통해 중요한 특징을 유지하면서도 불필요한 정보를 제거하는 효과가 있음
  • 중간 손실(Intermediate Loss)로 네트워크 중간에서 손실을 발생시키고 이를 역전파함으로써 경사 소실 문제 해결
  

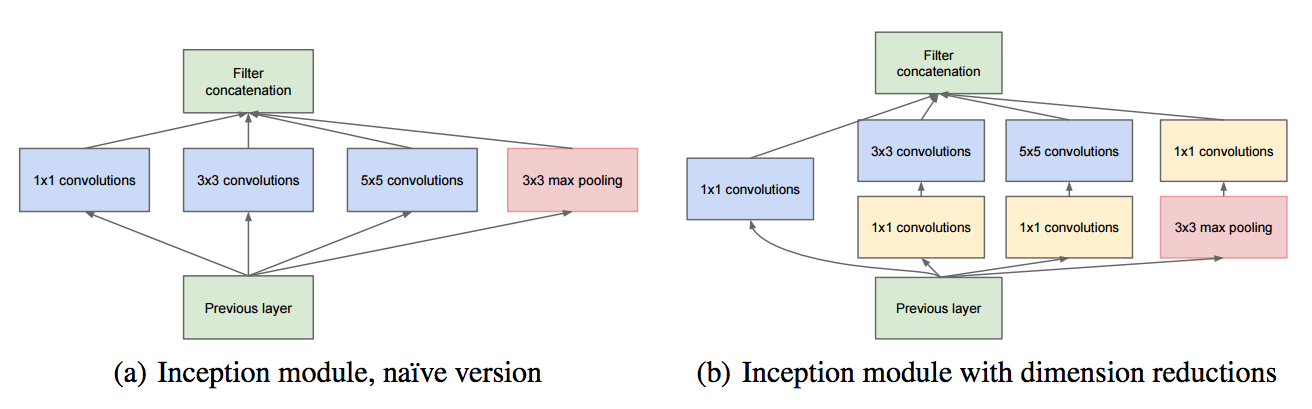
• 병목(bottleneck)**은 신경망에서 연산량과 메모리 사용을 줄이기 위해 특정 계층에서 데이터의 차원을 축소하는 기법

from tensorflow.keras.applications.inception_v3 import InceptionV3, preprocess_input, decode_predictions

inception = InceptionV3(include_top=True, weights='imagenet',
                        input_tensor=None, input_shape=None,
                        pooling=None, classes=1000)

Downloading data from https://storage.googleapis.com/tensorflow/keras-applications/inception_v3/inception_v3_weights_tf_dim_ordering_tf_kernels.h5
96112376/96112376 ━━━━━━━━━━━━━━━━━━━━ 0s 0us/step

• fish.jpg (https://upload.wikimedia.org/wikipedia/commons/7/7a/Goldfish_1.jpg)

!wget -O fish.jpg https://upload.wikimedia.org/wikipedia/commons/7/7a/Goldfish_1.jpg

--2024-11-07 08:56:00--  https://upload.wikimedia.org/wikipedia/commons/7/7a/Goldfish_1.jpg
Resolving upload.wikimedia.org (upload.wikimedia.org)... 198.35.26.112, 2620:0:863:ed1a::2:b
Connecting to upload.wikimedia.org (upload.wikimedia.org)|198.35.26.112|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 4648040 (4.4M) [image/jpeg]
Saving to: ‘fish.jpg’

fish.jpg            100%[===================>]   4.43M  20.1MB/s    in 0.2s    

2024-11-07 08:56:00 (20.1 MB/s) - ‘fish.jpg’ saved [4648040/4648040]

img = image.load_img('fish.jpg', target_size=(299, 299))
plt.imshow(img)

x = image.img_to_array(img)
x = preprocess_input(np.expand_dims(x,0))

preds = inception.predict(x)
print(decode_predictions(preds))

1/1 ━━━━━━━━━━━━━━━━━━━━ 9s 9s/step
[[('n01443537', 'goldfish', 0.9748253), ('n02701002', 'ambulance', 0.0023263083), ('n02606052', 'rock_beauty', 0.0019094164), ('n02607072', 'anemone_fish', 0.00066422834), ('n09256479', 'coral_reef', 0.00043224308)]]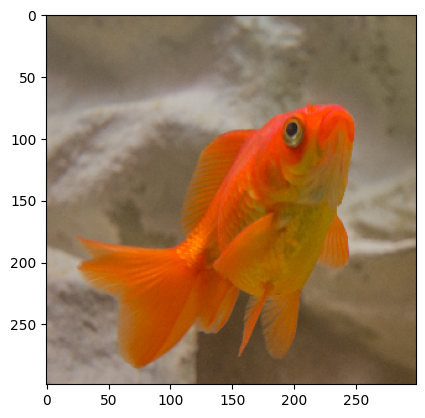

모델 깊이와 그라디언트 소실(Gradient Vanishing)

[이미지출처] resnet

ResNet(Residual Net)

• 네트워크의 깊이가 깊어질수록 경사가 소실되거나 폭발하는 문제를 해결하고자 함

• 병목 합성곱 계층을 추가하거나 크기가 작은 커널을 사용

• 152개의 훈련가능한 계층을 수직으로 연결하여 구성

• 모든 합성곱과 풀링 계층에서 패딩옵션으로 'SAME', stride=1 사용

• 3x3 합성곱 계층 다음마다 배치 정규화 적용, 1x1 합성곱 계층에는 활성화 함수가 존재하지 않음

  

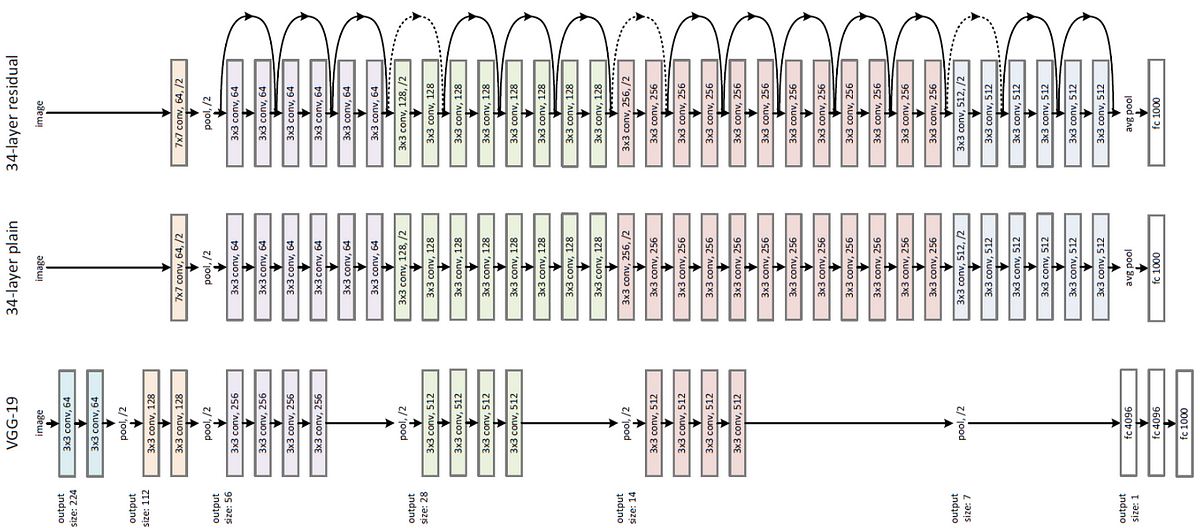
잔차 학습(Residual Learning)

• 잔차 연결은 일부 레이어를 건너뛰어(Skip Connection) 데이터가 신경망 구조의 후반부에 도달하는 또 다른 경로를 제공함으로써 정보를 보존하고 gradient가 계속 커지거나 작아지는 문제를 해결할 수 있음

• 잔차 학습을 통해 입력과 출력 사이의 변화를 학습하도록 유도하여, 더 깊은 네트워크에서도 효율적인 학습이 가능하게 함.

• 잔차 블록은 지름길 연결을 추가하여 경사를 효과적으로 전달하므로, 기울기 소실 문제를 완화하고 깊은 네트워크에서도 안정적인 학습을 도움.

• ResNet의 이러한 구조 덕분에 초깊은 네트워크에서도 학습이 가능해졌고, 일반화 성능이 뛰어난 모델로 평가됨

  

from tensorflow.keras.applications.resnet50 import ResNet50, preprocess_input, decode_predictions

resnet = ResNet50(include_top=True, weights='imagenet',
                  input_tensor=None, input_shape=None,
                  pooling=None, classes=1000)

Downloading data from https://storage.googleapis.com/tensorflow/keras-applications/resnet/resnet50_weights_tf_dim_ordering_tf_kernels.h5
102967424/102967424 ━━━━━━━━━━━━━━━━━━━━ 1s 0us/step

• bee.jpg (https://upload.wikimedia.org/wikipedia/commons/4/4d/Apis_mellifera_Western_honey_bee.jpg)

!wget -O bee.jpg https://upload.wikimedia.org/wikipedia/commons/4/4d/Apis_mellifera_Western_honey_bee.jpg

--2024-11-07 09:26:11--  https://upload.wikimedia.org/wikipedia/commons/4/4d/Apis_mellifera_Western_honey_bee.jpg
Resolving upload.wikimedia.org (upload.wikimedia.org)... 198.35.26.112, 2620:0:863:ed1a::2:b
Connecting to upload.wikimedia.org (upload.wikimedia.org)|198.35.26.112|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 2421052 (2.3M) [image/jpeg]
Saving to: ‘bee.jpg’

bee.jpg             100%[===================>]   2.31M  --.-KB/s    in 0.1s    

2024-11-07 09:26:11 (16.0 MB/s) - ‘bee.jpg’ saved [2421052/2421052]

img = image.load_img('bee.jpg', target_size=(224, 224))
plt.imshow(img)

x = image.img_to_array(img)
x = preprocess_input(np.expand_dims(x,0))

preds = resnet.predict(x)
print(decode_predictions(preds))

1/1 ━━━━━━━━━━━━━━━━━━━━ 4s 4s/step
[[('n02206856', 'bee', 0.9990979), ('n03530642', 'honeycomb', 0.00056267227), ('n02190166', 'fly', 0.00014306529), ('n02727426', 'apiary', 0.00010191327), ('n02219486', 'ant', 5.741178e-05)]]

Xception

• Inception module을 이용하여 depthwise convolution 적용

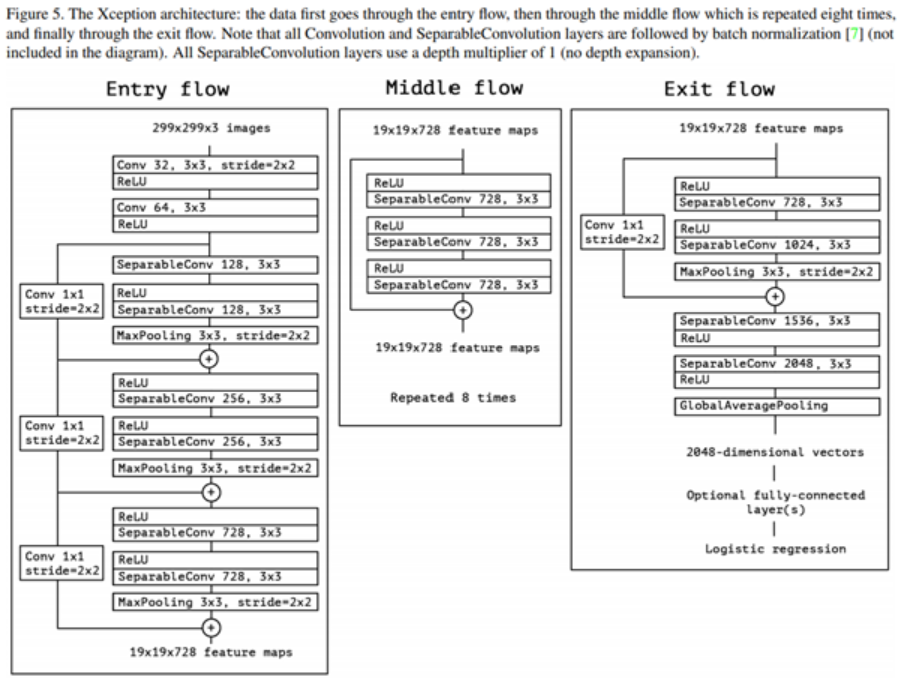
핵심 내용

• inception과 ResNet의 장점을 결합한 모델
• 일반적인 CNN 모델은 RGB 이미지를 입력으로 사용하는 경우, R, G, B 채널 전체에 대해 필터를 적용하여 각 필터가 모든 채널을 종합적으로 고려해 특징을 추출함
• Xception은 각 채널에 대해 개별적으로 합성곱 연산을 수행하는 깊이별 합성곱 (depthwise convolution)과, 그 결과를 다시 결합하는 점별 합성곱 (pointwise convolution)을 사용하여 계산량을 크게 줄일 수 있으며, 일반적인 합성곱보다 더 복잡한 패턴을 학습하는 데 유리한 장점을 가짐
• ResNet의 아이디어를 확장해서 skip connection을 도입해 학습을 안정화하고 정보 손실을 줄임

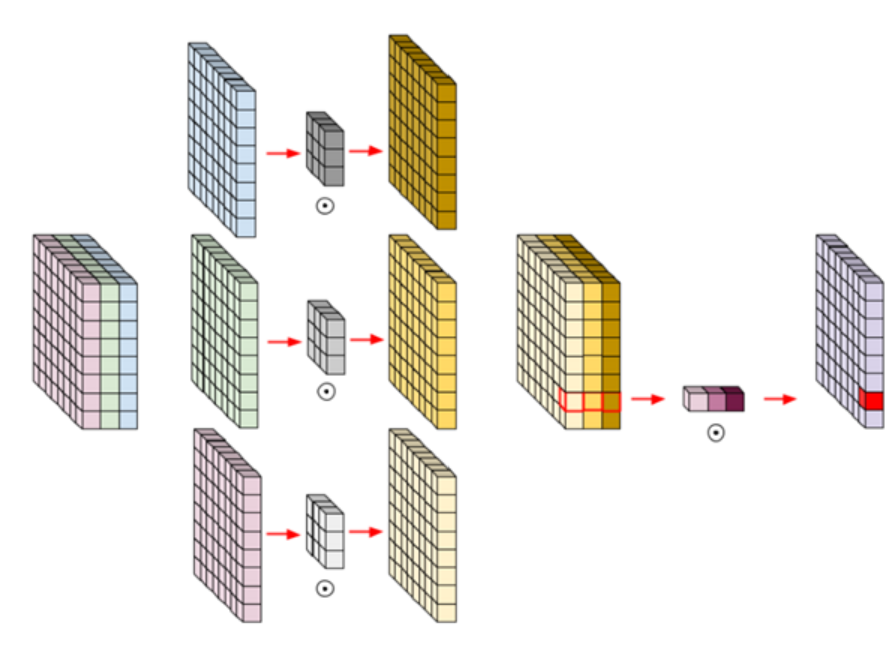
from tensorflow.keras.applications.mobilenet import MobileNet, preprocess_input, decode_predictions

mobilenet = MobileNet(include_top=True, weights='imagenet',
                      input_tensor=None, input_shape=None,
                      pooling=None, classes=1000)
mobilenet.summary()

Downloading data from https://storage.googleapis.com/tensorflow/keras-applications/mobilenet/mobilenet_1_0_224_tf.h5
17225924/17225924 ━━━━━━━━━━━━━━━━━━━━ 0s 0us/step

Model: "mobilenet_1.00_224"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type)                         ┃ Output Shape                ┃         Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ input_layer_9 (InputLayer)           │ (None, 224, 224, 3)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv1 (Conv2D)                       │ (None, 112, 112, 32)        │             864 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv1_bn (BatchNormalization)        │ (None, 112, 112, 32)        │             128 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv1_relu (ReLU)                    │ (None, 112, 112, 32)        │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_1 (DepthwiseConv2D)          │ (None, 112, 112, 32)        │             288 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_1_bn (BatchNormalization)    │ (None, 112, 112, 32)        │             128 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_1_relu (ReLU)                │ (None, 112, 112, 32)        │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_1 (Conv2D)                   │ (None, 112, 112, 64)        │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_1_bn (BatchNormalization)    │ (None, 112, 112, 64)        │             256 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_1_relu (ReLU)                │ (None, 112, 112, 64)        │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pad_2 (ZeroPadding2D)           │ (None, 113, 113, 64)        │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_2 (DepthwiseConv2D)          │ (None, 56, 56, 64)          │             576 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_2_bn (BatchNormalization)    │ (None, 56, 56, 64)          │             256 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_2_relu (ReLU)                │ (None, 56, 56, 64)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_2 (Conv2D)                   │ (None, 56, 56, 128)         │           8,192 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_2_bn (BatchNormalization)    │ (None, 56, 56, 128)         │             512 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_2_relu (ReLU)                │ (None, 56, 56, 128)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_3 (DepthwiseConv2D)          │ (None, 56, 56, 128)         │           1,152 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_3_bn (BatchNormalization)    │ (None, 56, 56, 128)         │             512 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_3_relu (ReLU)                │ (None, 56, 56, 128)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_3 (Conv2D)                   │ (None, 56, 56, 128)         │          16,384 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_3_bn (BatchNormalization)    │ (None, 56, 56, 128)         │             512 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_3_relu (ReLU)                │ (None, 56, 56, 128)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pad_4 (ZeroPadding2D)           │ (None, 57, 57, 128)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_4 (DepthwiseConv2D)          │ (None, 28, 28, 128)         │           1,152 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_4_bn (BatchNormalization)    │ (None, 28, 28, 128)         │             512 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_4_relu (ReLU)                │ (None, 28, 28, 128)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_4 (Conv2D)                   │ (None, 28, 28, 256)         │          32,768 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_4_bn (BatchNormalization)    │ (None, 28, 28, 256)         │           1,024 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_4_relu (ReLU)                │ (None, 28, 28, 256)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_5 (DepthwiseConv2D)          │ (None, 28, 28, 256)         │           2,304 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_5_bn (BatchNormalization)    │ (None, 28, 28, 256)         │           1,024 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_5_relu (ReLU)                │ (None, 28, 28, 256)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_5 (Conv2D)                   │ (None, 28, 28, 256)         │          65,536 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_5_bn (BatchNormalization)    │ (None, 28, 28, 256)         │           1,024 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_5_relu (ReLU)                │ (None, 28, 28, 256)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pad_6 (ZeroPadding2D)           │ (None, 29, 29, 256)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_6 (DepthwiseConv2D)          │ (None, 14, 14, 256)         │           2,304 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_6_bn (BatchNormalization)    │ (None, 14, 14, 256)         │           1,024 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_6_relu (ReLU)                │ (None, 14, 14, 256)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_6 (Conv2D)                   │ (None, 14, 14, 512)         │         131,072 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_6_bn (BatchNormalization)    │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_6_relu (ReLU)                │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_7 (DepthwiseConv2D)          │ (None, 14, 14, 512)         │           4,608 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_7_bn (BatchNormalization)    │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_7_relu (ReLU)                │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_7 (Conv2D)                   │ (None, 14, 14, 512)         │         262,144 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_7_bn (BatchNormalization)    │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_7_relu (ReLU)                │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_8 (DepthwiseConv2D)          │ (None, 14, 14, 512)         │           4,608 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_8_bn (BatchNormalization)    │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_8_relu (ReLU)                │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_8 (Conv2D)                   │ (None, 14, 14, 512)         │         262,144 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_8_bn (BatchNormalization)    │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_8_relu (ReLU)                │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_9 (DepthwiseConv2D)          │ (None, 14, 14, 512)         │           4,608 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_9_bn (BatchNormalization)    │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_9_relu (ReLU)                │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_9 (Conv2D)                   │ (None, 14, 14, 512)         │         262,144 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_9_bn (BatchNormalization)    │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_9_relu (ReLU)                │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_10 (DepthwiseConv2D)         │ (None, 14, 14, 512)         │           4,608 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_10_bn (BatchNormalization)   │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_10_relu (ReLU)               │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_10 (Conv2D)                  │ (None, 14, 14, 512)         │         262,144 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_10_bn (BatchNormalization)   │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_10_relu (ReLU)               │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_11 (DepthwiseConv2D)         │ (None, 14, 14, 512)         │           4,608 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_11_bn (BatchNormalization)   │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_11_relu (ReLU)               │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_11 (Conv2D)                  │ (None, 14, 14, 512)         │         262,144 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_11_bn (BatchNormalization)   │ (None, 14, 14, 512)         │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_11_relu (ReLU)               │ (None, 14, 14, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pad_12 (ZeroPadding2D)          │ (None, 15, 15, 512)         │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_12 (DepthwiseConv2D)         │ (None, 7, 7, 512)           │           4,608 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_12_bn (BatchNormalization)   │ (None, 7, 7, 512)           │           2,048 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_12_relu (ReLU)               │ (None, 7, 7, 512)           │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_12 (Conv2D)                  │ (None, 7, 7, 1024)          │         524,288 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_12_bn (BatchNormalization)   │ (None, 7, 7, 1024)          │           4,096 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_12_relu (ReLU)               │ (None, 7, 7, 1024)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_13 (DepthwiseConv2D)         │ (None, 7, 7, 1024)          │           9,216 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_13_bn (BatchNormalization)   │ (None, 7, 7, 1024)          │           4,096 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_dw_13_relu (ReLU)               │ (None, 7, 7, 1024)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_13 (Conv2D)                  │ (None, 7, 7, 1024)          │       1,048,576 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_13_bn (BatchNormalization)   │ (None, 7, 7, 1024)          │           4,096 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_pw_13_relu (ReLU)               │ (None, 7, 7, 1024)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ global_average_pooling2d             │ (None, 1, 1, 1024)          │               0 │
│ (GlobalAveragePooling2D)             │                             │                 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout (Dropout)                    │ (None, 1, 1, 1024)          │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv_preds (Conv2D)                  │ (None, 1, 1, 1000)          │       1,025,000 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ reshape_2 (Reshape)                  │ (None, 1000)                │               0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ predictions (Activation)             │ (None, 1000)                │               0 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘

 Total params: 4,253,864 (16.23 MB)

 Trainable params: 4,231,976 (16.14 MB)

 Non-trainable params: 21,888 (85.50 KB)

• crane.jpg (https://p1.pxfuel.com/preview/42/50/534/europe-channel-crane-harbour-crane-harbour-cranes-cranes-transport.jpg)

!wget -O crane.jpg https://p1.pxfuel.com/preview/42/50/534/europe-channel-crane-harbour-crane-harbour-cranes-cranes-transport.jpg

--2024-11-07 09:44:54--  https://p1.pxfuel.com/preview/42/50/534/europe-channel-crane-harbour-crane-harbour-cranes-cranes-transport.jpg
Resolving p1.pxfuel.com (p1.pxfuel.com)... 104.21.12.22, 172.67.151.78, 2606:4700:3037::ac43:974e, ...
Connecting to p1.pxfuel.com (p1.pxfuel.com)|104.21.12.22|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 86911 (85K) [image/jpeg]
Saving to: ‘crane.jpg’

crane.jpg           100%[===================>]  84.87K  --.-KB/s    in 0.01s   

2024-11-07 09:44:54 (6.00 MB/s) - ‘crane.jpg’ saved [86911/86911]

img = image.load_img('crane.jpg', target_size=(224, 224))
plt.imshow(img)

x = image.img_to_array(img)
x = preprocess_input(np.expand_dims(x,0))

preds = mobilenet.predict(x)
print(decode_predictions(preds))

WARNING:tensorflow:5 out of the last 6 calls to <function TensorFlowTrainer.make_predict_function.<locals>.one_step_on_data_distributed at 0x7d034f6fdcf0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has reduce_retracing=True option that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.


1/1 ━━━━━━━━━━━━━━━━━━━━ 3s 3s/step
[[('n03126707', 'crane', 0.96338284), ('n03216828', 'dock', 0.027054528), ('n03240683', 'drilling_platform', 0.0047102487), ('n03344393', 'fireboat', 0.0022202074), ('n03532672', 'hook', 0.0005047548)]]

DenseNet

• 각 층은 모든 이전 층으로 부터 출력을 입력으로 받음(밀집 블록(dense block))
• 이러한 조밀 연결은 특징 맵을 재활용하며 네트워크 깊이가 깊어지더라도 이전 층에서 추출된 정보를 유지해 효율적인 학습을 가능하게 함
• 특징지도의 크기를 줄이기 위해 풀링 연산 적용 필요
• 각 층이 이전 모든 층의 출력을 활용할 수 있어 불필요한 특성 학습을 줄여 고유한 필터를 학습하지 않아도 되기 때문에 네트워크의 파라미터 수가 줄어듬.
• 위 특징으로 인해 메모리와 계산량을 줄이고, 경량 모델을 만들 수 있음.
• 밀집 블록(dense block)과 전이층(transition layer)으로 구성
• 전이층 : 1x1 컨볼루션과 평균값 풀링(APool)으로 구성 -> 특징 맵의 크기와 채널 수를 줄임

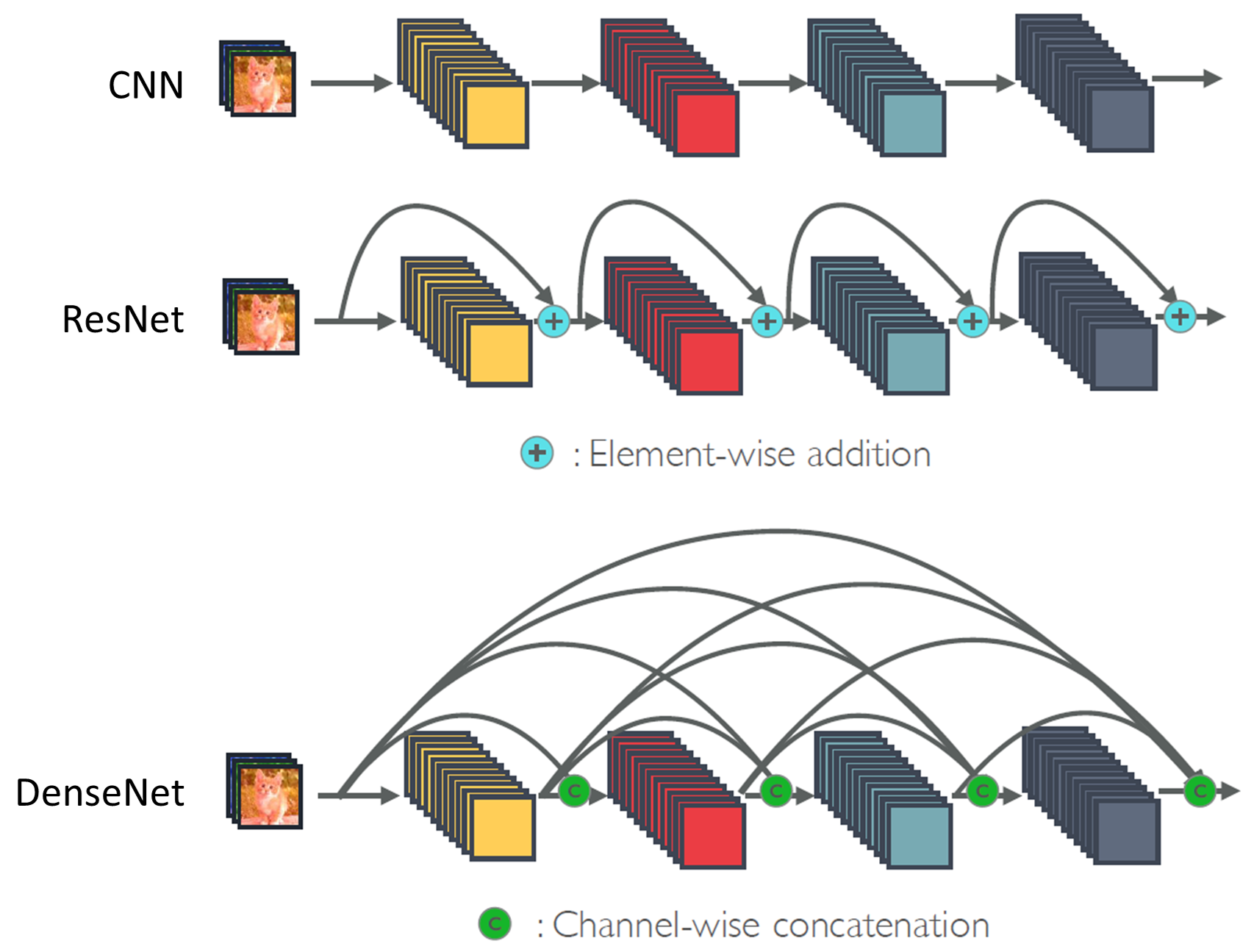
from tensorflow.keras.applications.densenet import DenseNet201, preprocess_input, decode_predictions

densenet = DenseNet201(include_top=True, weights='imagenet',
                  input_tensor=None, input_shape=None,
                  pooling=None, classes=1000)

Downloading data from https://storage.googleapis.com/tensorflow/keras-applications/densenet/densenet201_weights_tf_dim_ordering_tf_kernels.h5
82524592/82524592 ━━━━━━━━━━━━━━━━━━━━ 1s 0us/step

• zebra.jpg (https://upload.wikimedia.org/wikipedia/commons/f/f0/Zebra_standing_alone_crop.jpg)

!wget -O zebra.jpg https://upload.wikimedia.org/wikipedia/commons/f/f0/Zebra_standing_alone_crop.jpg

--2024-11-07 10:49:10--  https://upload.wikimedia.org/wikipedia/commons/f/f0/Zebra_standing_alone_crop.jpg
Resolving upload.wikimedia.org (upload.wikimedia.org)... 198.35.26.112, 2620:0:863:ed1a::2:b
Connecting to upload.wikimedia.org (upload.wikimedia.org)|198.35.26.112|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 188036 (184K) [image/jpeg]
Saving to: ‘zebra.jpg’


zebra.jpg             0%[                    ]       0  --.-KB/s               
zebra.jpg           100%[===================>] 183.63K  --.-KB/s    in 0.05s   

2024-11-07 10:49:11 (3.35 MB/s) - ‘zebra.jpg’ saved [188036/188036]

img = image.load_img('zebra.jpg', target_size=(224, 224))
plt.imshow(img)

x = image.img_to_array(img)
x = preprocess_input(np.expand_dims(x,0))

preds = densenet.predict(x)
print(decode_predictions(preds))

WARNING:tensorflow:6 out of the last 7 calls to <function TensorFlowTrainer.make_predict_function.<locals>.one_step_on_data_distributed at 0x7d034faa2c20> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has reduce_retracing=True option that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.


1/1 ━━━━━━━━━━━━━━━━━━━━ 18s 18s/step
[[('n02391049', 'zebra', 0.9299189), ('n01518878', 'ostrich', 0.020074163), ('n02423022', 'gazelle', 0.012079946), ('n02397096', 'warthog', 0.00449013), ('n02422106', 'hartebeest', 0.003128522)]]

NasNet

• 강화학습을 활용한 자동화된 아키텍처 탐색(Neural Architecture Search (NAS))으로 최적의 신경망 구조를 효율적으로 설계
• NASNet에서 찾아낸 최적의 구조는 사람의 설계로는 발견하기 어려운 방식으로 조합되어 있어, 기존의 수작업 모델보다 효율적이면서도 성능이 뛰어난 경우가 많음
• 높은 성능과 효율성을 동시에 만족하는 최적의 아키텍처 발견

from tensorflow.keras.applications.nasnet import NASNetLarge, preprocess_input, decode_predictions

nasnet = NASNetLarge(include_top=True, weights='imagenet',
                  input_tensor=None, input_shape=None,
                  pooling=None, classes=1000)

Downloading data from https://storage.googleapis.com/tensorflow/keras-applications/nasnet/NASNet-large.h5
359748576/359748576 ━━━━━━━━━━━━━━━━━━━━ 2s 0us/step

• notebook.jpg (https://cdn.pixabay.com/photo/2016/07/11/03/35/macbook-1508998_1280.jpg)

!wget -O notebook.jpg https://cdn.pixabay.com/photo/2016/07/11/03/35/macbook-1508998_1280.jpg

--2024-11-07 11:01:16--  https://cdn.pixabay.com/photo/2016/07/11/03/35/macbook-1508998_1280.jpg
Resolving cdn.pixabay.com (cdn.pixabay.com)... 172.64.147.160, 104.18.40.96, 2606:4700:4400::ac40:93a0, ...
Connecting to cdn.pixabay.com (cdn.pixabay.com)|172.64.147.160|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 270631 (264K) [binary/octet-stream]
Saving to: ‘notebook.jpg’

notebook.jpg        100%[===================>] 264.29K  --.-KB/s    in 0.07s   

2024-11-07 11:01:16 (3.55 MB/s) - ‘notebook.jpg’ saved [270631/270631]

img = image.load_img('notebook.jpg', target_size=(331, 331))
plt.imshow(img)

x = image.img_to_array(img)
x = preprocess_input(np.expand_dims(x,0))

preds = nasnet.predict(x)
print(decode_predictions(preds))

1/1 ━━━━━━━━━━━━━━━━━━━━ 21s 21s/step
[[('n03832673', 'notebook', 0.79398525), ('n03642806', 'laptop', 0.048131146), ('n04264628', 'space_bar', 0.0341737), ('n03085013', 'computer_keyboard', 0.020013861), ('n03777754', 'modem', 0.011280097)]]

EfficientNet

• EfficientNet은 EfficientNet-B0라는 기준 모델을 시작점으로 함. 이 모델은 신경망 아키텍처 검색(NAS)을 통해 찾은 효율적인 구조임
• NAS를 통해 발견된 B0 아키텍처는 이미 효율성과 성능을 극대화한 구조로, 이를 바탕으로 다른 버전(B1~B7)들이 파생됨
• NASNet처럼 각 모델의 모든 세부 구조를 탐색하지 않고, B0 모델을 시작으로 Compound Scaling 공식을 적용해 네트워크의 깊이, 너비, 해상도를 균형 있게 확장함
• Compound Scaling은 깊(레이어수), 너비(채널수/필터수), 해상도(입력이미지크기)를 여러 시도와 탐색을 통해 찾은 비율로 함께 확장해 모델의 성능과 자원 효율성을 동시에 최적화하는 기법임

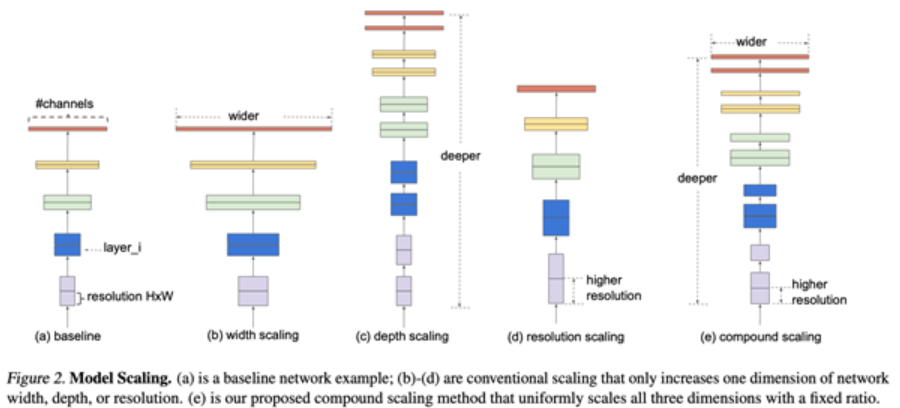
from tensorflow.keras.applications.efficientnet import EfficientNetB1, preprocess_input, decode_predictions

efficientnet = EfficientNetB1(include_top=True, weights='imagenet',
                  input_tensor=None, input_shape=None,
                  pooling=None, classes=1000)

Downloading data from https://storage.googleapis.com/keras-applications/efficientnetb1.h5
32148312/32148312 ━━━━━━━━━━━━━━━━━━━━ 0s 0us/step

• plane.jpg (https://upload.wikimedia.org/wikipedia/commons/1/12/Plane-in-flight.jpg)

!wget -O plane.jpg https://upload.wikimedia.org/wikipedia/commons/1/12/Plane-in-flight.jpg

--2024-11-07 11:17:00--  https://upload.wikimedia.org/wikipedia/commons/1/12/Plane-in-flight.jpg
Resolving upload.wikimedia.org (upload.wikimedia.org)... 198.35.26.112, 2620:0:863:ed1a::2:b
Connecting to upload.wikimedia.org (upload.wikimedia.org)|198.35.26.112|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 487351 (476K) [image/jpeg]
Saving to: ‘plane.jpg’

plane.jpg           100%[===================>] 475.93K  --.-KB/s    in 0.1s    

2024-11-07 11:17:00 (3.75 MB/s) - ‘plane.jpg’ saved [487351/487351]

img = image.load_img('plane.jpg', target_size=(240, 240))
plt.imshow(img)

x = image.img_to_array(img)
x = preprocess_input(np.expand_dims(x,0))

preds = efficientnet.predict(x)
print(decode_predictions(preds))

1/1 ━━━━━━━━━━━━━━━━━━━━ 11s 11s/step
[[('n02690373', 'airliner', 0.7460463), ('n04592741', 'wing', 0.079652555), ('n04552348', 'warplane', 0.05106398), ('n04266014', 'space_shuttle', 0.016655603), ('n01494475', 'hammerhead', 0.00594431)]]