[Flutter] Custom Clipper - 2. 도형과 곡선

기초편에서 나만의 직선을 그려서 도형을 만드는 방법을 학습했으니, 이제 도형과 곡선을 마스터 해보자

그리고 직선을 그릴때 좀더 유용한 메서드들이 있으니 그것도 추가로 학습해보자.

이번에도 가로 세로 200의 정사각형 네모를 기준으로 설명하겠다.

도형을 그리는 메서드

(1) addRect, addRRect

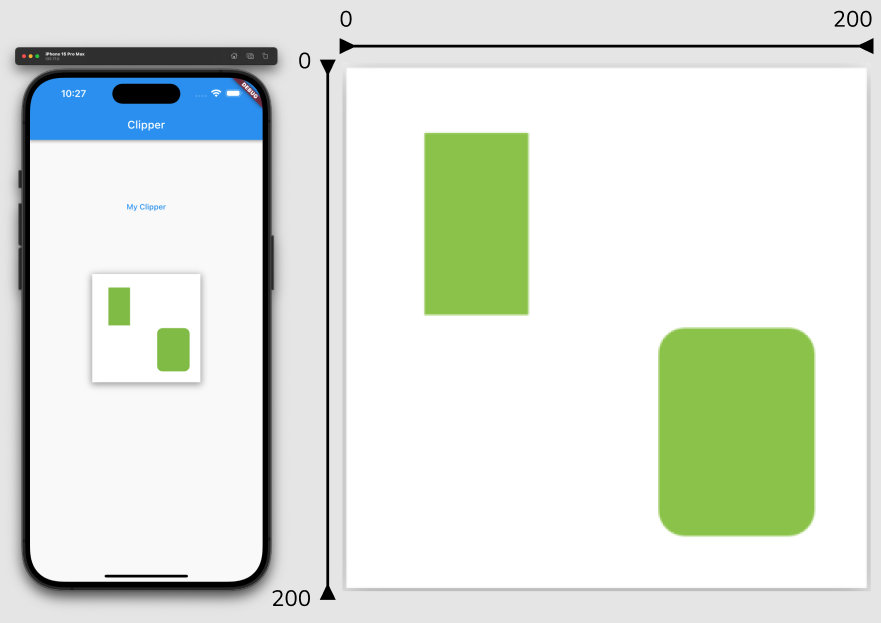
• addRect는 직사각형, addRRect는 모서리가 동그란 직사각형을 그리는데 사용한다.
  addRect는 Rect클래스를 통해 직사각형을 그릴 좌표와 크기를 지정하고
  유사한 addRRect는 RRect클래스를 통해 동그란 직사각형을 그린다.
  RRect는 Rect보다 radius 인자 1개를 더 받는다.
• addRect는 현재 내 위치에 영향을 받지 않는다.
  Rect클래스가 지정된 좌표로 사각형을 그린다.

class MyClipper extends CustomClipper<Path> {
  MyClipper();
  @override
  Path getClip(Size size) {
    Path path = Path()
      ..addRect(Rect.fromCenter(center: Offset(50, 60), width: 40, height: 70))
      ..addRRect(RRect.fromLTRBR(120, 100, 180, 180, Radius.circular(10)))
      ..close();
    return path;
  }

  @override
  bool shouldReclip(CustomClipper<Path> oldClipper) {
    return true;
  }
}

(2) addOval

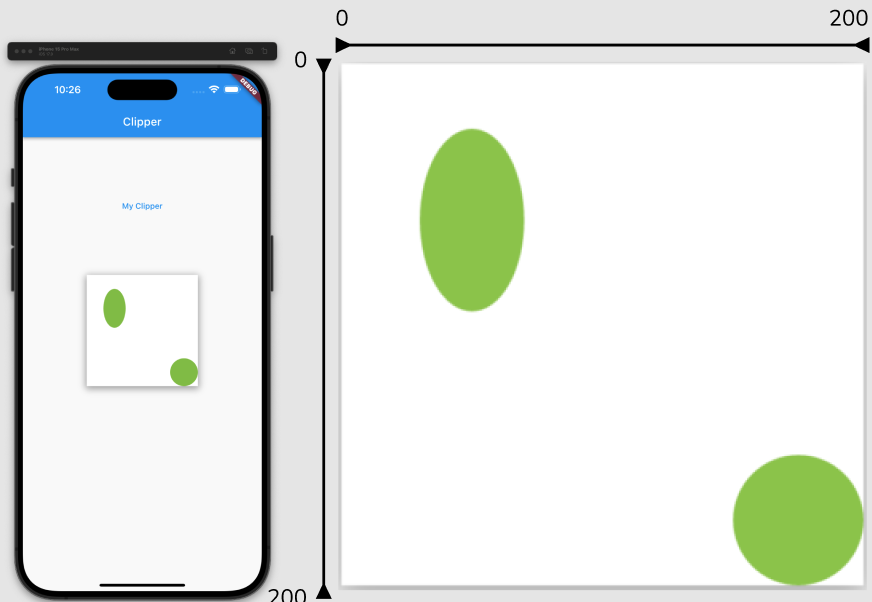
• addRect와 사용법이 같으나 이번에는 원형 도형을 그려준다.
  Rect의 높이와 너비가 달라 직사각형 모양이 되는 경우 타원형으로 그려진다.

class MyClipper extends CustomClipper<Path> {
  MyClipper();
  @override
  Path getClip(Size size) {
    Path path = Path()
      ..addOval(Rect.fromCenter(center: Offset(50, 60), width: 40, height: 70))
      ..addOval(Rect.fromPoints(Offset(150, 150), Offset(200, 200)))
      ..close();
    return path;
  }

  @override
  bool shouldReclip(CustomClipper<Path> oldClipper) {
    return true;
  }
}

(3) **addPolygon**

• Offset() 의 배열을 인자로 받아서 개성적인 다각형을 그려준다.

class MyClipper extends CustomClipper<Path> {
  List<Offset> polygon = [
    Offset(100, 20),
    Offset(85, 65),
    Offset(45, 64),
    Offset(75, 95),
    Offset(58, 140),
    Offset(100, 110),
    Offset(142, 140),
    Offset(125, 95),
    Offset(155, 64),
    Offset(115, 65),
    Offset(100, 20),
  ];

  @override
  Path getClip(Size size) {
    Path path = Path()
      ..addPolygon(polygon, false)
      ..close();
    return path;
  }

  @override
  bool shouldReclip(CustomClipper<Path> oldClipper) {
    return true;
  }
}

곡선을 그리는 메서드

(1) quadraticBezierTo() - 2차 베지에 곡선

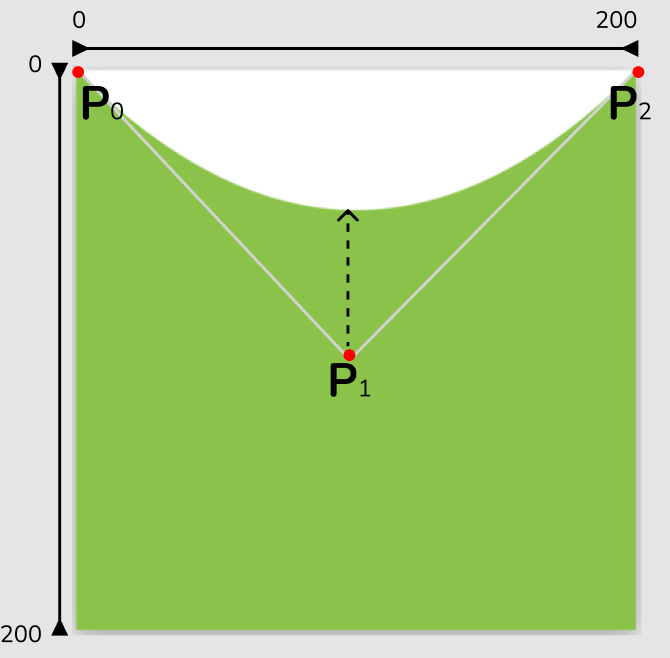
• 시작 포인트(현재 위치, P0)와 컨트롤 포인트(구심점이 될 위치, P1) 그리고 도착 포인트(P2)를 지정하고 곡선을 그린다.
• ..quadraticBezierTo(x1, y1, x2, y2) 로 선언하며
  곡선을 그리는 시작점과 도착점(x2, y2) 까지 P1(x1, y1)방향으로 커브를 그리는 곡선을 그려준다.
• 수학적 부분을 제외하고 정리하려니 설명이 어렵지만, 우선 시작점 끝점을 정하고 어느쪽을 중점으로 곡선을 그릴건지 찝어보면 된다.
  정밀하게 곡선을 그리려고 한다면 피그마 등 그래픽 툴에는 비슷한 기능이 있으니 디자이너가 있다면 물어보자.

class MyClipper extends CustomClipper<Path> {
  @override
  Path getClip(Size size) {
    double w = size.width;
    double h = size.height;

    Path path = Path()
      ..quadraticBezierTo(w / 2, h / 2, w, 0) // 정 가운데를 중심으로
      ..lineTo(w, h)
      ..lineTo(0, h)
      ..close();
    return path;
  }

  @override
  bool shouldReclip(CustomClipper<Path> oldClipper) {
    return true;
  }
}

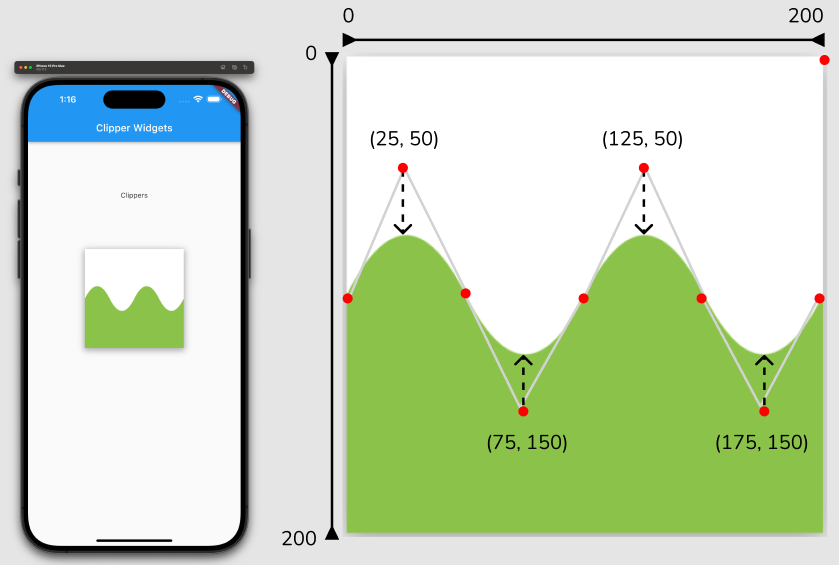
• 곡면을 어느 포인트를 기점으로 잡는지에 따라 다양한 연출이 가능하다.

class MyClipper extends CustomClipper<Path> {
  @override
  Path getClip(Size size) {
    double w = size.width;
    double h = size.height;

		// 편의를 위해 w/2 가 아니라 100 같은 정수로 써두겠다.
    Path path = Path()
      ..moveTo(0, h / 2)
      ..quadraticBezierTo(25, 50, 50, 100)
      ..quadraticBezierTo(75, 150, 100, 100)
      ..quadraticBezierTo(125, 50, 150, 100)
      ..quadraticBezierTo(175, 150, 200, 100)
      ..lineTo(w, h)
      ..lineTo(0, h)
      ..close();
    return path;
  }

  @override
  bool shouldReclip(CustomClipper<Path> oldClipper) {
    return true;
  }
}

(2) cubicTo() - 3차 베지에 곡선

• quadraticBezierTo() 메서드에서 컨트롤 포인트를 2개로 늘렸다고 생각하면 된다.
• ..cubicTo(x1, y1, x2, y2, x3, y3)형태로 선언하며 맨 마지막에 들어가는 (x3, y3)이 도착점이고, 시작점 부터 도착점(x3, y3)까지 가는 중에 첫 번째 조절점(x1, y1)과 두 번째 조절점(x2, y2)의 좌표를 입력하여 두 조절점을 이용해 곡선을 그린다.

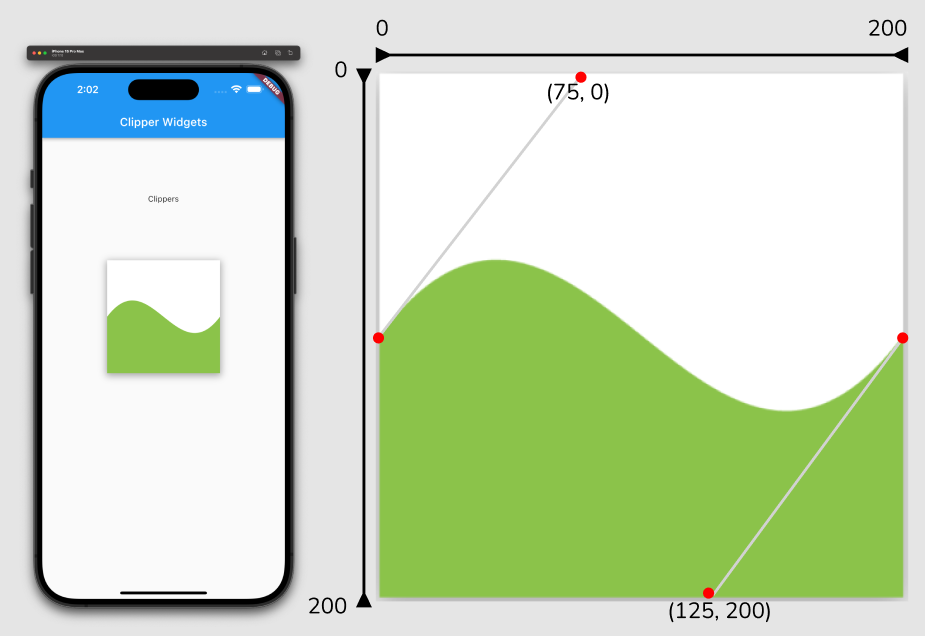
class MyClipper extends CustomClipper<Path> {
  @override
  Path getClip(Size size) {
    double w = size.width;
    double h = size.height;

    Path path = Path()
      ..moveTo(0, h / 2)
      ..cubicTo(75, 0, 125, 200, 200, 100)
      ..lineTo(w, h)
      ..lineTo(0, h)
      ..close();
    return path;
  }

  @override
  bool shouldReclip(CustomClipper<Path> oldClipper) {
    return true;
  }
}

(3) arcToPoint()

• 시작점에서 지정된 점 까지 호를 그린다. radius(반지름)을 지정해서 굴곡을 줄 수 있으며 시계방향과 반시계방향 설정이 가능하다.
• ..arcToPoint(Offset(dx, dy), radius: radius, clockwise: clockwise = true) 형식으로 선언한다.
  Offset(dx, dy)은 끝점, radius는 반지름, clockwise는 호를 그리는 방향을 설정할수 있다.

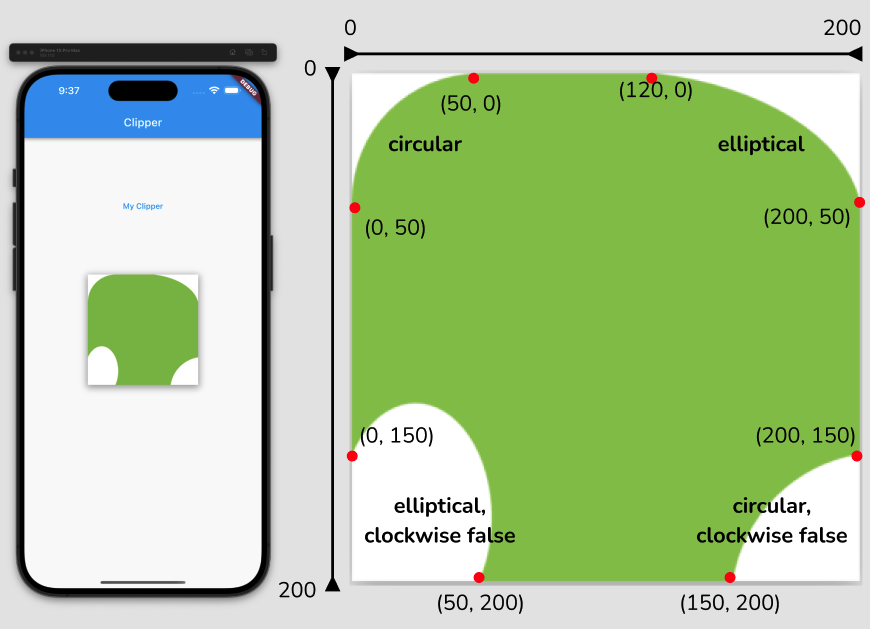
class MyClipper extends CustomClipper<Path> {

  @override
  Path getClip(Size size) {
    Path path = Path()
      ..moveTo(0, 50)
      ..arcToPoint(
        Offset(50, 0),
        radius: Radius.circular(50),
      )
      ..lineTo(120, 0)
      ..arcToPoint(Offset(200, 50), radius: Radius.elliptical(100, 60))
      ..lineTo(200, 150)
      ..arcToPoint(Offset(150, 200),
          radius: Radius.circular(60),
          clockwise: false // 기본 true, 역시계방향 할 때만 사용하며 false로.
          )
      ..lineTo(50, 200)
      ..arcToPoint(Offset(0, 150),
          radius: Radius.elliptical(20, 30), clockwise: false)
      ..close();
    return path;
  }

  @override
  bool shouldReclip(CustomClipper<Path> oldClipper) {
    return true;
  }
}

(4) arcTo()

• 시작 점과 끝 점을 지정한 후, 시작 각과 끝 각을 지정하여 호를 그리는 메서드이다.
• ..arcTo(rect, startAngle, sweepAngle, forceMoveTo) 이렇게 선언한다. 첫 인자인 Rect 클래스는 fromPoints, fromCircle, fromLTRB, fromLTWH 등으로 다양하게 사용할 수 있는데 이들을 파악히게 앞서서 원의 시작각과 끝각을 어떻게 지정하는지 알아야 한다.
  

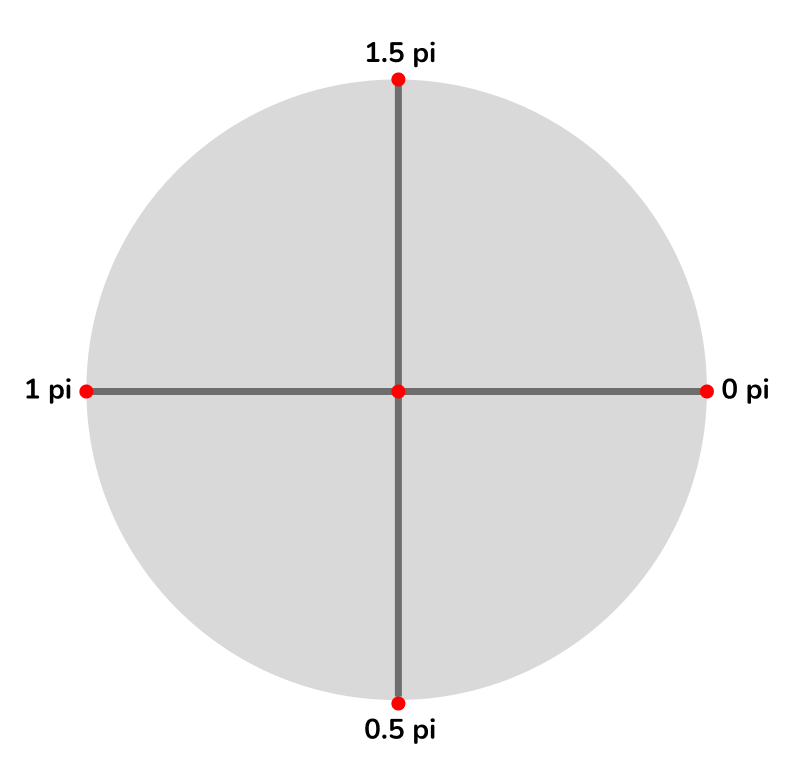
• 가운데 점으로 부터 오른쪽이 0pi고, 시계방향으로 돌면서 90도 마다 0.5pi씩 늘어난다.
  pi는 dart의 math를 import 해서 사용하면 되며 이전 arcToPoint와 달리 arcTo는 완전히 원을 그리는 메서드이다 보니 이 부분을 알고있어야 사용이 쉽다.

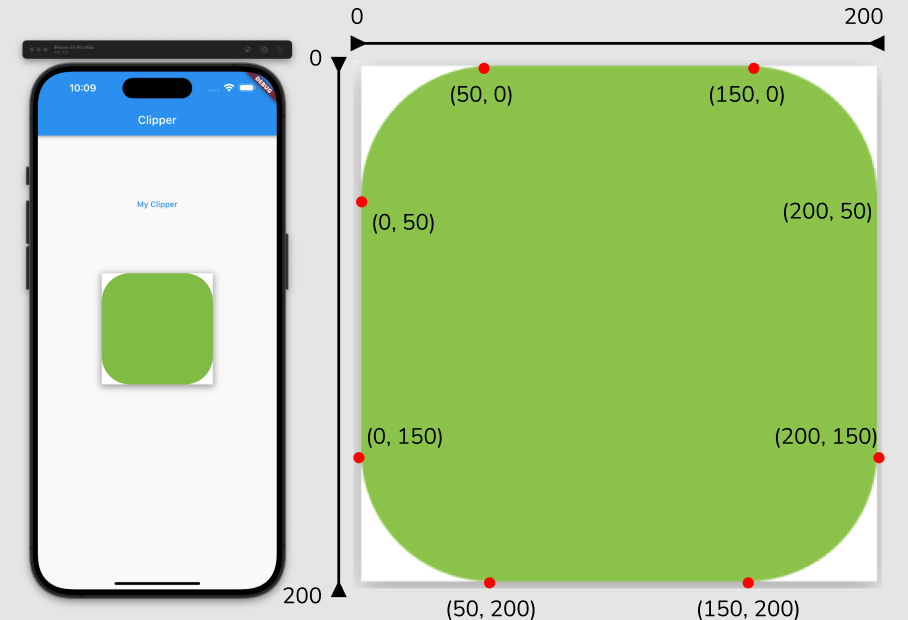
class MyClipper extends CustomClipper<Path> {

  @override
  Path getClip(Size size) {
    Path path = Path()
      ..moveTo(0, 50)
      ..arcTo(Rect.fromCenter(center: Offset(50, 50), width: 100, height: 100),
          1 * pi, 0.5 * pi, false)
      ..lineTo(150, 0)
      ..arcTo(
          Rect.fromCircle(center: Offset(150, 50), radius: 50),
          1.5 * pi,
          0.5 * pi, // 얼마나 호를 그을건지
          false)
      ..lineTo(200, 150)
      ..arcTo(Rect.fromLTRB(100, 100, 200, 200), 2 * pi, 0.5 * pi, false)
      ..lineTo(50, 200)
      ..arcTo(Rect.fromLTWH(0, 100, 100, 100), 0.5 * pi, 0.5 * pi, false)
      ..close(); 
    return path;
  }

  @override
  bool shouldReclip(CustomClipper<Path> oldClipper) {
    return true;
  }
}

기타 유용한 메서드

(1) addPath

• Path 클래스의 내부 메서드로 다른 Path를 캔버스에 추가로 그려준다. Path.addPath(새로운 path, 시작 포인트); 로 선언한다. myPath.addPath(newPath, Offset(dx/dy));
  

(2) relativeLineTo

• lineTo 메서드 처럼 선을 그려준다.
  하지만 내 현재 포인트에서 dx, dy만큼 이동한 좌표로 선을 그린다.

  `..relativeLineTo(dx, dy)`로 선언한다.