Block Coding
- block coding은 physical layer에서 연속적인 0을 방지하기 위해 사용되었다.
- error detection/correction에서도 사용된다.
- dataword : a block of original message
- codeword : block-coded message
- Generate an n-bit codeword from a k-bit dataword
- dataword : k bits
- codeword : n bits
- r : redundancy
- r : n - k
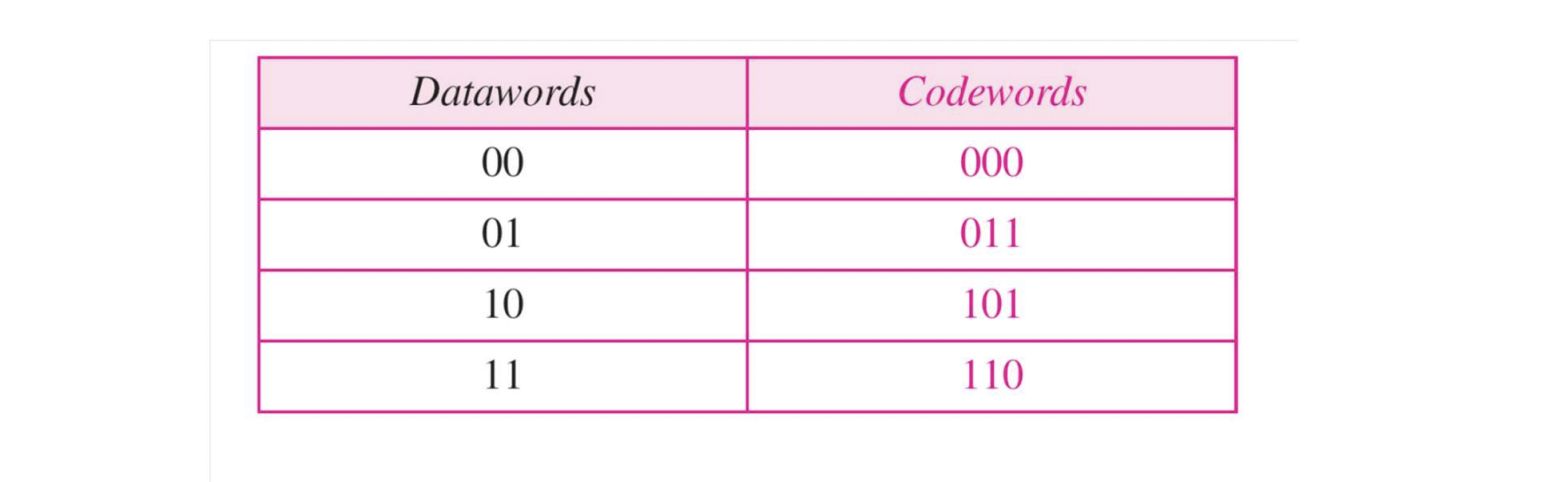
- 위 그림을 토대로, sender sends "011"
- "011" received : dataword가 "01"이라고 판단한다
- "111" received : error가 발생했다고 판단한다
- "000" received : dataword가 "00"이라고 판단한다 (X)
- This codeword set은 1-bit error는 detect할 수 있지만, 2-bit error는 detect할 수 없다.
- Prove that this scheme always detect 1-bit error
: 1-bit error가 발생했을 때, 그 값이 다른 codeword에 존재하면 detect가 불가능하다.
하지만 codeword들의 set을 보면, 1이 무조건 짝수개임을 볼 수 있다.
이러면 1-bit가 바뀌어도, 다른 곳에 존재할 수가 없다.
따라서 1-bit error를 검출할 수 있다.
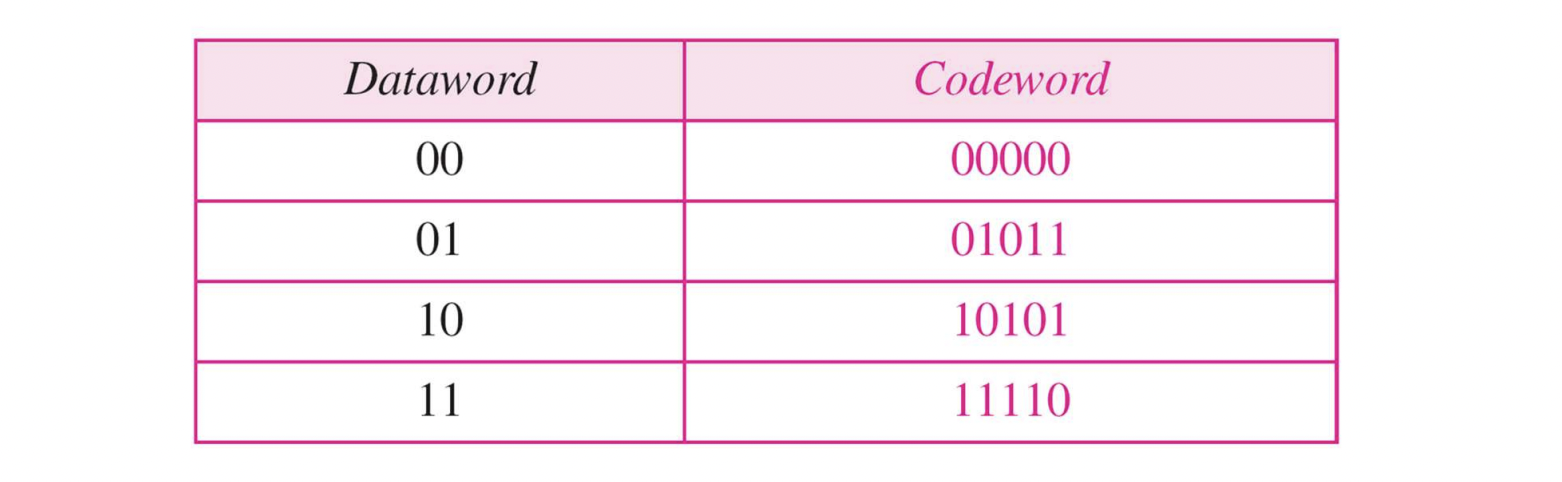
-
위 그림에서, sender sends "01011"
-
"01001" received : 1-bit error 확인
- the closest codeword : "01001"
- dataword가 "01"이라고 추측한다.
-
"00001" received : 2-bit error 확인
- 이 경우에, closest codeword가 00000이다.
- 즉, 2-bit error는 correct할 수 없다.
-
3-bit error는 검출이 불가능하다.
-
-
이렇게 쓰면, 검출하는 능력은 좋아지지만,
2bit 보내는 데 5bit를 쓰고 있으니까 속도가 40% 줄어든다
trade off
Hamming distance
- Number of different bits between two codewords
몇 bit 바꿔야 하는지.
- CT : transitted codeword
- CR : received codeword
- d(CT, CR) = n means there was n-bit error
- MHD(minimum hamming distance)
- 첫 번째 예시 : MHD = 2
-> 1 bit까지 검출 가능 - 두 번째 예시 : MHD = 3
-> 2 bit까지 검출 가능
- 첫 번째 예시 : MHD = 2
- To detect an s-bit error, MHD of the codeword set must be lager than s
- To correct a t-bit error, MHD of the codeword set must be larger tha 2t
Linear block codes
- 2 codeword를 뽑아서 XOR을 시킨다. 만약 결과가 다시 codeword set에 있다면, 그 codeword set을 linear block codes라고 부른다.
MHD of linear block codes
- 0으로만 채워진 애 말고, 다른 codeword들에 있는 1 개수 중 최솟값이 MHD가 된다.
Simple Parity Check Codes
- k-bit dataword -> (k+1)-bit codeword
- Add 1 bit(parity bit)
- 이 parity bit은 codeword가 짝수개의 1을 가지게 만들어야 한다.
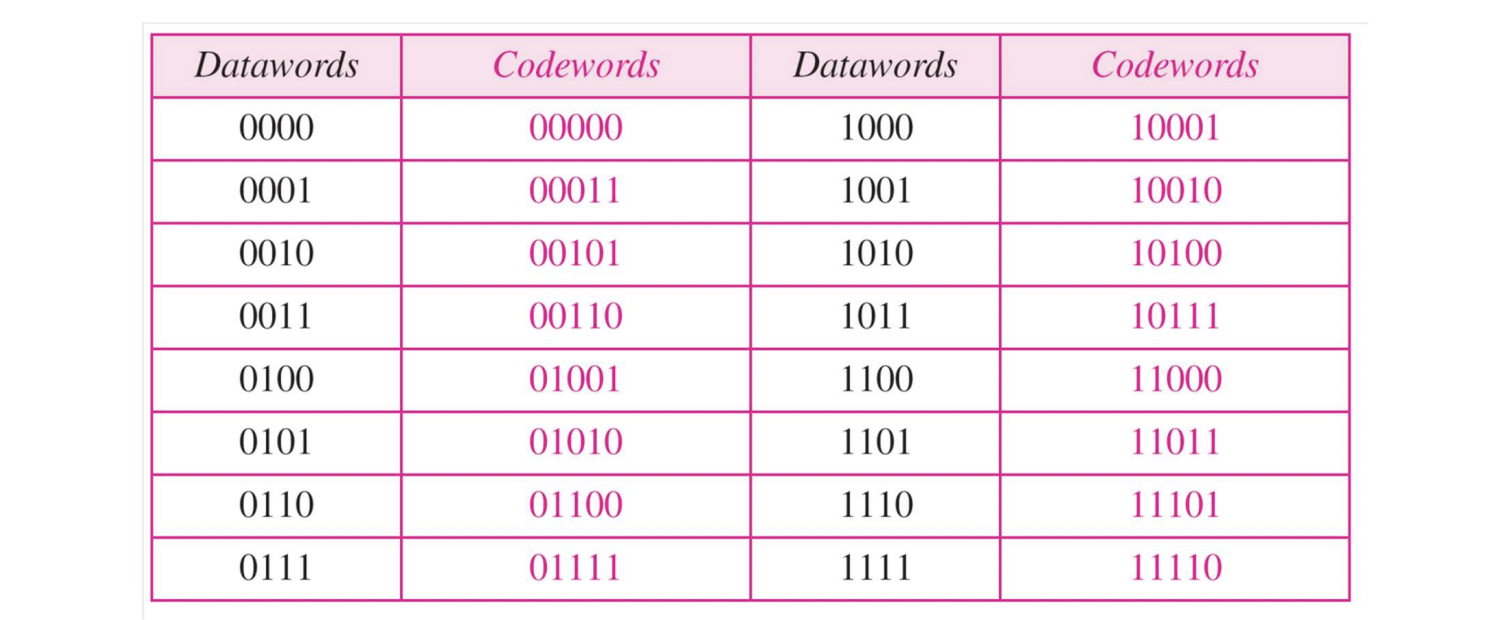
- n = k + 1
- dmin = 2
- 이미 1이 짝수개인 애한테는 0 붙여주고, 홀수개인 애한테는 1 붙여준다.
Q. Sender sends dataword "1011" using parity check codes - codeword is '10111'
(1). '10111' receives
(2). '10011' receives
(3). '10110' receives
A.
(1). good
(2). 1-bit error. 검출 가능
(3). 1-bit error. 검출 가능. parity에서 문제
Q. Sender sends "10111"
(1). '00110' receives
(2). '01011' receives
A.
(1). 2-bit error. 검출 불가능. parity가지고도 불가능
(2). 3-bit error. 검출 가능
- Parity Check
- can detect 1-bit errors
- cannot detect 2-bit errors
- can detect 3-bit errors
- cannot detect 4-bit errors
- Parity check codes can detect odd-bit errors
- Pretty good~
2-dimensional parity
- 오른쪽과 아래에 parity를 각각 만든다
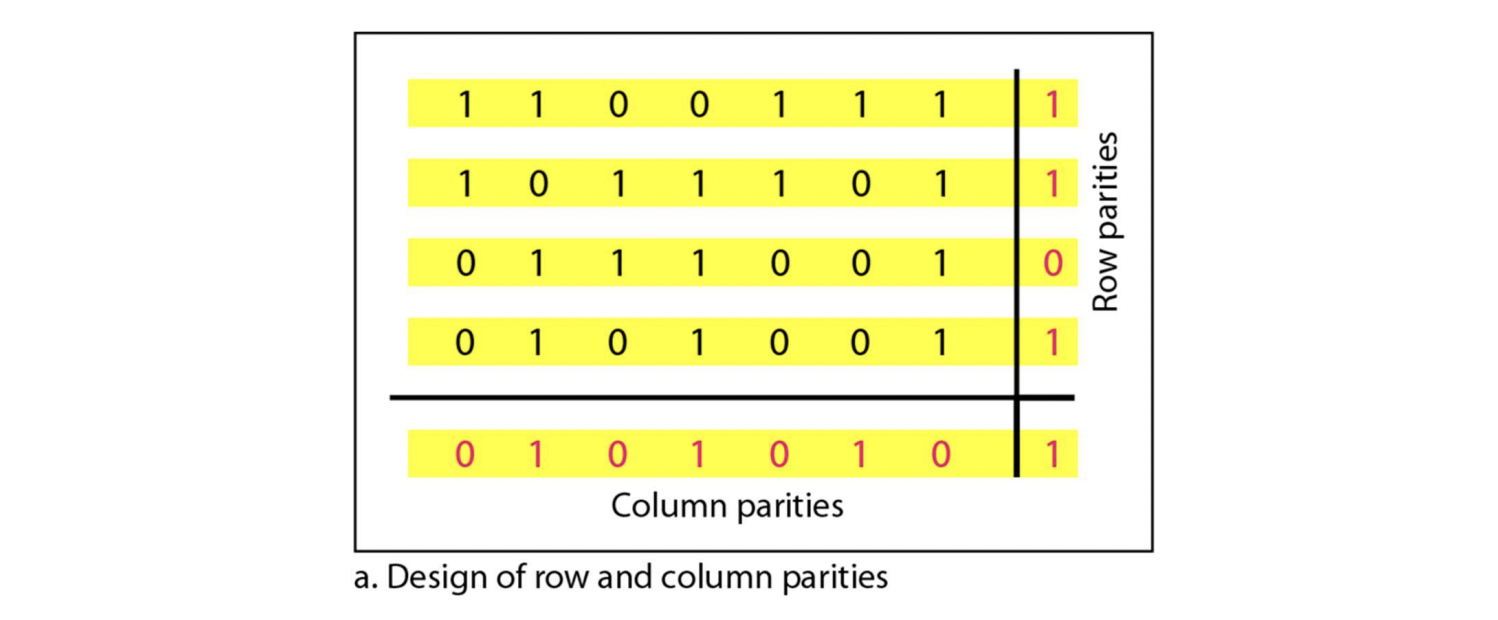
- 예시로 공부하는게 나은 듯
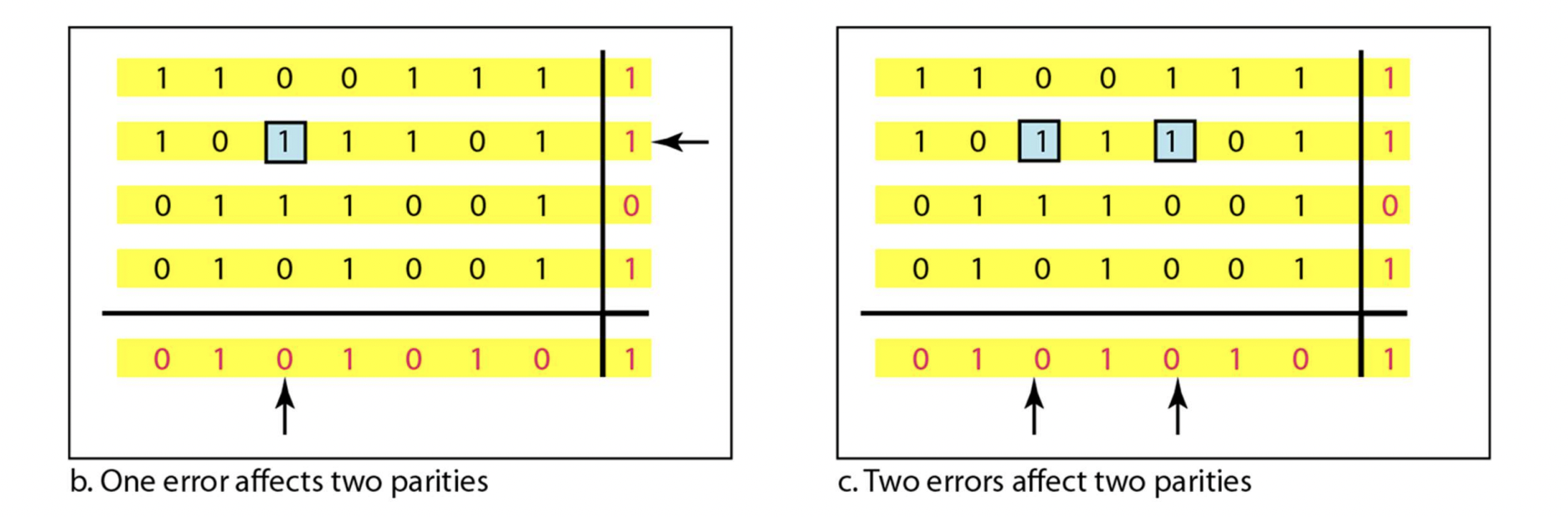
- b. 파란색 네모친 부분이 0으로 바뀌면, 가로/세로 모두 오류가 있는 걸 확인하고, 수정도 가능하다. 즉, detect, correction 모두 가능하다
- c. 모든 row는 완벽하지만, 두 column에서 문제가 있음을 확인한다. 하지만 어떤 row에서 문제가 있는지 확인할 순 없다. detect 가능, correction 불가능
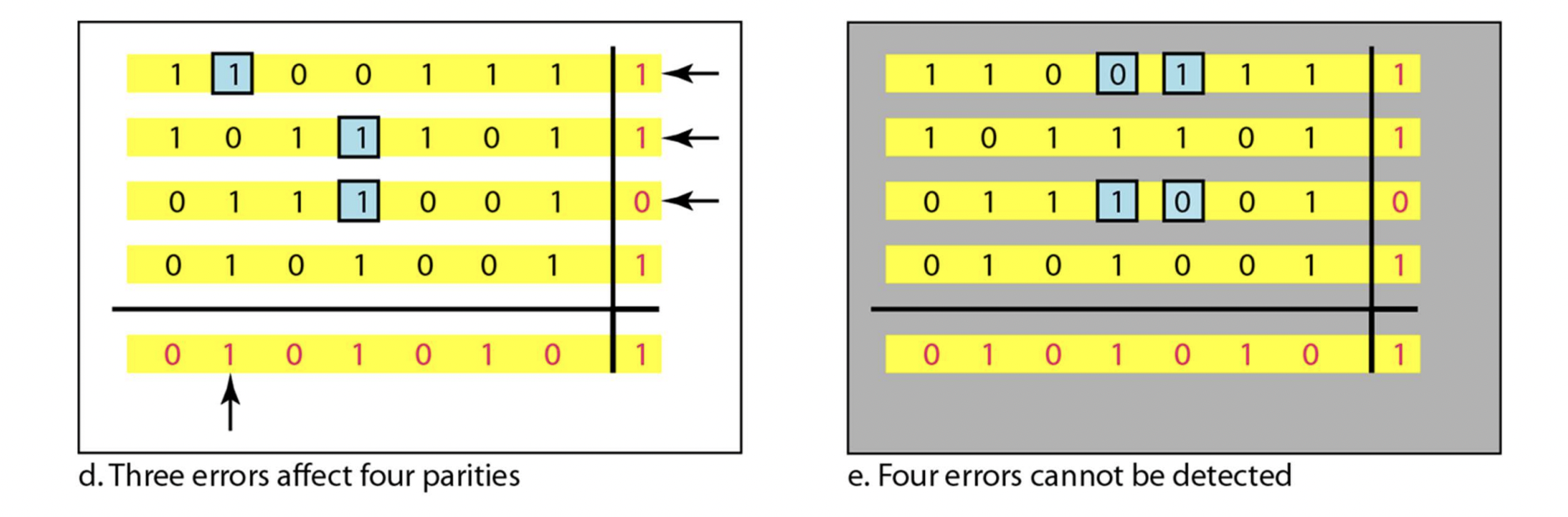
- d. 왼쪽 위에 있는 애는 에러 위치까지 정확하게 알 수 있다. 하지만 밑에 두 개는 column은 완벽하지만, 두 개의 row에서 문제가 있음을 확인한다. 어떤 column인지 확인이 불가능하다. detect 가능, correction 불가능
- e. 최악의 경우이다. detect correct 모두 불가능하다. 이렇게까지 나오는 경우가 거의 드물고, 몇몇 4 error case는 detect가 가능하다.
Performance of 2-D parity
- 1 bit error : detect and correct
- 2 bit error : detect
- 3 bit error : detect
- 4 bit error : cannot detect
- 하나라도 n-bit error 케이스들 중, 하나라도 detect 못하는 케이스가 있으면, 그건 cannot detect이다.
Hamming (n, k) code
- dmin = 3 (detect 2-bit, correct 1-bit)
- convert a k-bit dataword into an n-bit codeword
Hamming (7, 4) code
- 4-bit dataword -> 7-bit codeword
- 16가지 -> 알아서 mapping한다. dmin만 유지시킨다.
- 이 부분은 직접 써가면서 공부하는게 더 나을 듯 싶다.

Why (7, 4)?
- To correct a 1-bit error in an n-bit codeword,
the receiver should be able to correctly pick one of the following cases :- No error
- 1st bit is error
- 2nd bit is error
... - nth bit is error
- total n+1 cases.
- So, for a n-bit codeword, n+1 pieces of information is needed to correct a 1-bit error.
- To embed n+1 pieces of information, we need log2(n+1) bits.
- Hamming code uses minimum cost to correct 1-bit errors.
There cannot be a better way - Hamming code is described as a perfect code. optimal
- 예를 들어, 4 bit dataword를 보내려고 할 때, 추가해주는 check bit가 x개 있다고 하자.
- 그럼 우리는 그 추가해주는 x개의 bit로 가능한 1-bit error를 구분해주어야 한다.
- 위처럼 가능한 1-bit error 케이스는 총 8가지이다.
- x개로 8개를 구분하기 위한 가장 최소의 x는 3이다.
- 그래서 (7, 4)당
Voting
- The simplest way to increase hamming distance
- Convert '0' into N number of '0's
- If n = 3, '0' -> '000', '1' -> '111'
- Make hamming distance N
- '010' receives -> interpreted as 0
because the codeword has more 0s than 1s -> voting
- Efficiency of voting = 1/3 = 33.3%
- Efficiency of hamming(7, 4) = 4/7 = 57.1%
Summary
- Hamming (7, 4)의 이유를 다시 생각해보자
- Recall that to correct 1-bit error in 7-bit codeword, wee need 3 control bits. (8 pieces of information)
- 일반적으로, 우리가 (2k - 1) bit codeword가 있다고 하면, 1 bit를 correct하기 위해 k개의 control bit가 필요하다.
- size of the control bit = k
- size of the codeword = 2k - 1
- size of the dataword = 2k - 1 - k
- k = 3, (7, 4)
k = 4, (15, 11)
k = 5, (31, 26) - k가 커질수록 efficiency가 증가한다. ()
- 하지만, k가 커질수록 2-bit error가 발생할 확률이 높아진다.
7개 중 2개 틀리는 것 보다는 31개에서 2개 틀릴 확률이 높은 건 당연하다.
2-bit error는 검출도 못하는데.. detection rate decreases