
Good Relational Designs
-
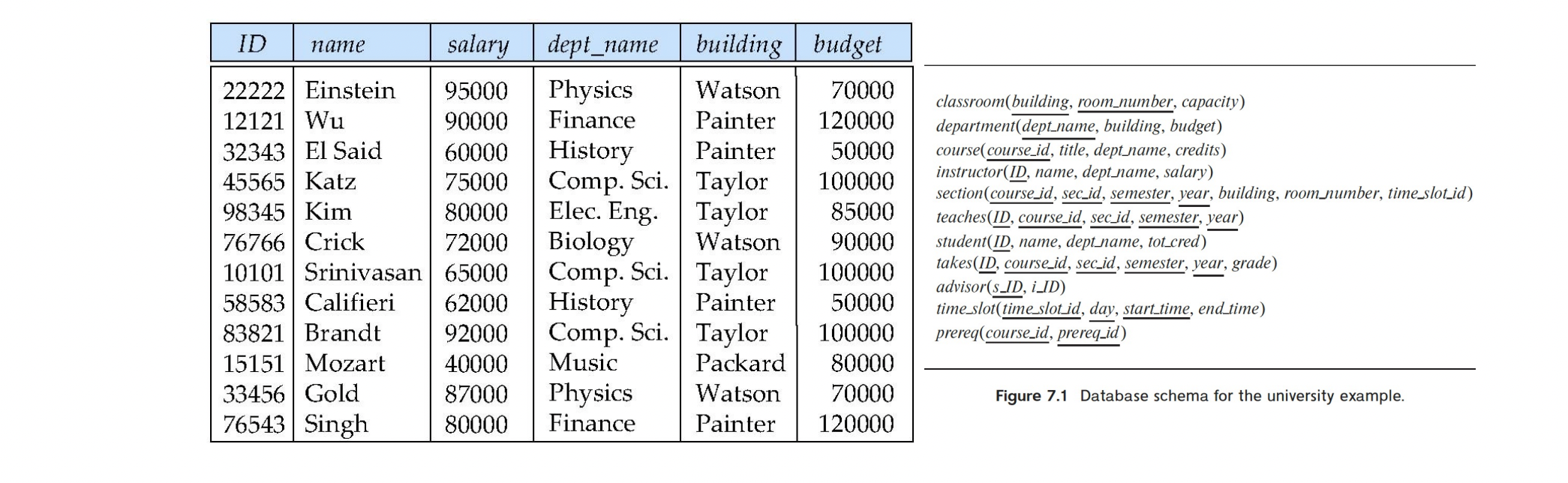
instructor와 department를 합쳐서 in_dep table을 만들었다고 하자.
(which represents the natural join on the relations instructor and department) -
위 테이블은 좋지 않다.
-
정보의 반복이 발생한다.
dept_name에 Comp.Sci.가 3번이나 반복된다
- 이렇게 되면 나중에 update할 때 일관성이 깨질 가능성이 있다.
- 예를 들면 Comp.sci의 budget을 update할 때 3번을 해주어야 모든 데이터가 정상적으로 업데이트 된다. 2번만 하게 되면 하나는 예전 budget값을 갖고 있는 문제가 생긴다. -
Null value를 사용해야 하는 경우가 생긴다
instructor가 없는 신생 학과를 추가할 수가 없다.
-
Decomposition
- 위 예시에서 in_dep를 좋은 table로 만들기 위한 방법은 이를 instructor와 department 두 개의 schema로 나누는 것이다.
- 그렇다고 무작정 decompose하는 것은 좋지 않다.
Lossy Decomposition
-
employee(ID, name, street, city, salary) 를
employee1(ID, name)과 employee2(name, street, city, salary)로 나눈다고 해보자. -
일단 쪼갤 필요도 없는 경우고, 잘못 쪼갰다. employee2의 경우에 동명이인인 경우, tuple을 구분할 수 없는 문제가 생길 것이다.
-
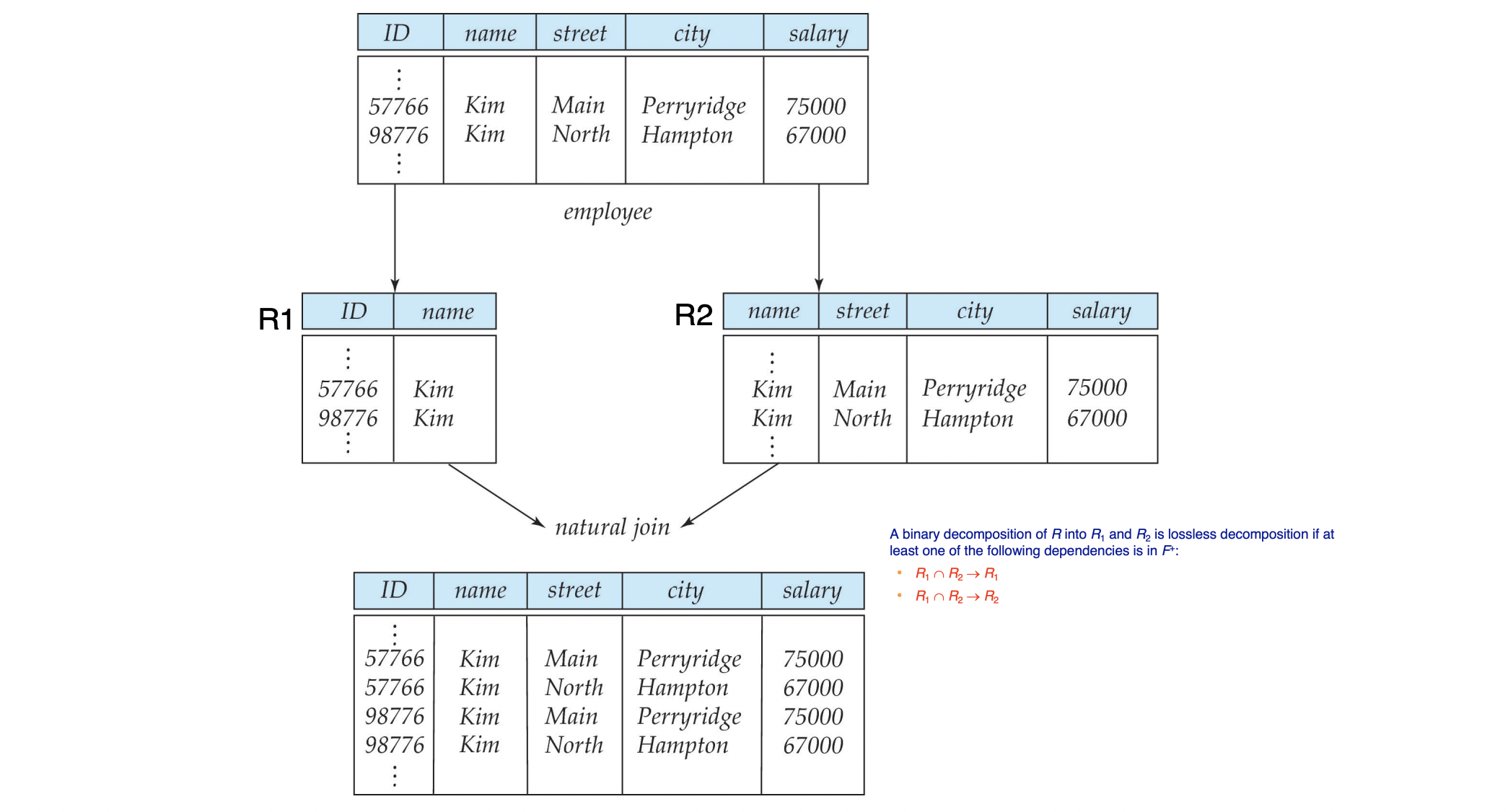
더 문제는, 이들을 name으로 join했을 때, 가짜 정보가 들어오게 된다. 이를 loss라고 한다. 정보가 없어졌다는 게 아니고, 가짜 정보가 들어왔다는 것을 의미한다.
-
위 그림에서 확인할 수 있듯이, 다시 join한 테이블에서 두 Kim에 대한 정확한 주소를 알 수 없다.
-
이러한 decomposition을 Lossy Decomposition이라고 한다.
Lossless Decomposition
- Let R be a relation schema and let R1 and R2 form a decomposition of R.
That is R = R1 U R2 - We say that the decomposition is a lossless decomposition if there is no loss of information by replacing R with the two relaion schemas R1 U R2
Normalization Theory
-
어떤 relation R이 "good form" 인지를 먼저 확인해야 한다.
-
위에 in_dep table은 good form이라고 할 수 없다.
언급했듯이 정보의 중복이 발생하여 data 일관성이 떨어지고, insert하기도 어렵기 때문이다. -
이처럼 어떤 relation R이 "good form"이 아닐 때에는 이를 {R1, ..., Rn}으로 decompose해야 한다.
- 이 때, 각각의 relation Ri들은 good form이어야 하고,
- 그 decomposition은 lossless decomposition이어야 한다.
-
Our theory is based on
Functional dependencies and Multivalued dependencies
Functional Dependencies
- DB에 있는 data들에는 다양한 제약조건(constraint, rule)이 있다.
- 예를 들면, each student와 instructor는 unique한 ID가 있어야 하고, 이름은 하나만 있어야 하며, 하나의 department에만 속해야 한다.
- relation에서 이러한 모든 constraint를 만족하는 instance를 legal instance라고 한다.
(여기서 instance는 tuple이랑 동일하게 생각해도 될 것 같다.)
- Require that the values for a certain set of attributes determines uniquely the value for another set of attributes.
primary key를 통해 다른 애들을 unique하게 식별한다는 의미..? 같다..
Definition
Let R be a relation schema that å ⊂ R and ß ⊂ R.
(å와 ß는 attribute의 부분집합이다)
The functional dependency å -> ß holds on R
if and only if
for any legal relation r(R), whenever any two tuples t1 and t2 of r agree on the attributes å, they also agree on the attributes ß. That is,
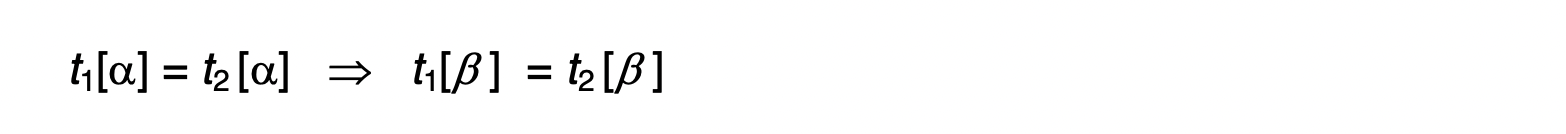
-
즉, å에 대한 t1과 t2의 tuple value가 서로 같으면, ß에 대한 tuple value도 같을 때, å->ß 라고 한다.
-
(1). 모든 tuple에서 primary key는 unique하게 식별되기 때문에 primary key에 대해서는 tuple value가 같아진다는 것이 불가능하다.
이걸 반대로 생각하면, 가정이 false이기 때문에 primary key에서 나머지에 대해 무조건 functional dependency가 있다.primary key를 제외하고도 다른 dependency가 있으면, good form이 아니다. -
(2). 만약 å에 대해 t1 t2의 tuple values가 다르면, 뒤에 ß에 대한 값은 신경 쓸 필요도 없다. 이미 끝이다.
Example
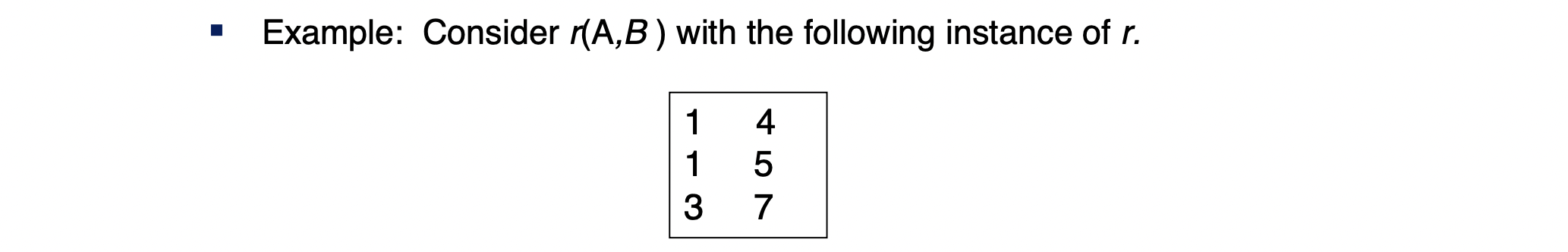
- A는 1, 1, 3이고 B는 4, 5, 7이다.
- 결과적으로, B->A는 hold, A->B는 NOT hold.
Closure
- F를 functional dependency들의 집합이라고 하자.
- 이 때, F에 있는 dependency들에 의해 imply되는 다른 dependency가 있다.
- If A -> B and B -> C, then we can infer that A -> C
- 이렇게 F에 대해 logically imply되는 모든 functional dependency들의 집합을 F의 closure라고 한다.
Key
-
K is a superkey for relation schema R
if and only if
K->R
: 모든 tuple을 unique하게 식별할 수 있어야 한다. -
K is a candidate key for R
if and only if
K->R and for no å⊂K, å->R
: 그냥 비슷하게 minimal하다고 생각하면 된다. 얘보다 더 작은 애(부분집합)은 그런 애가 없다, 요런 느낌 -
Functional dependency는 superkey로 표현할 수 없는 여러 제약조건들을 표현할 수 있게 해준다.
- in_dep(
ID, name, salay,dept_namebuilding, budget) 에서, - 우리는 다음과 같은 dependency가 hold하기를 기대한다 :
- dept_name -> building
- ID -> building
- 또한, 다음과 같은 dependency는 hold하지 않기를 기대한다 :
- dept_name -> salary
이러한 constraint는 key로는 표현이 불가능하다(???)
functional dependency로 표현하였다. - in_dep(
Use
functional dependency는 다음과 같은 상황에서 이용된다 :
- To test relaions to see if they are legal under a given set of functional dependencies.
- relation r 이 functional dependency set F 에서 legal하면,
이걸 r satisfies F 라고 말한다.
- relation r 이 functional dependency set F 에서 legal하면,
- To specify constraints on the set of legal relations
- R의 모든 legal relation이 functional dependency set F를 satisfy하면,
이걸 F holds on R 라고 말한다.
- R의 모든 legal relation이 functional dependency set F를 satisfy하면,
- 주의 : 특정 instance에서 판단하면 안된다.
- 운 좋게 name이 다 달라서 functional dependency를 만족할 수도 있는데, 이런 건 포함하지 않는다.
Trivial Functional Dependency
-
A->A
자기 자신으로 가는 거 -
AB->A
부분집합으로 가는거 -
언제나 만족한다. trivial
-
In general, å->ß is trivial if ß⊂å
Test lossless decomposition
functional dependency는 특정 decomposition이 lossless인지를 보여준다.

- 역은 참이 아니다. False
Example
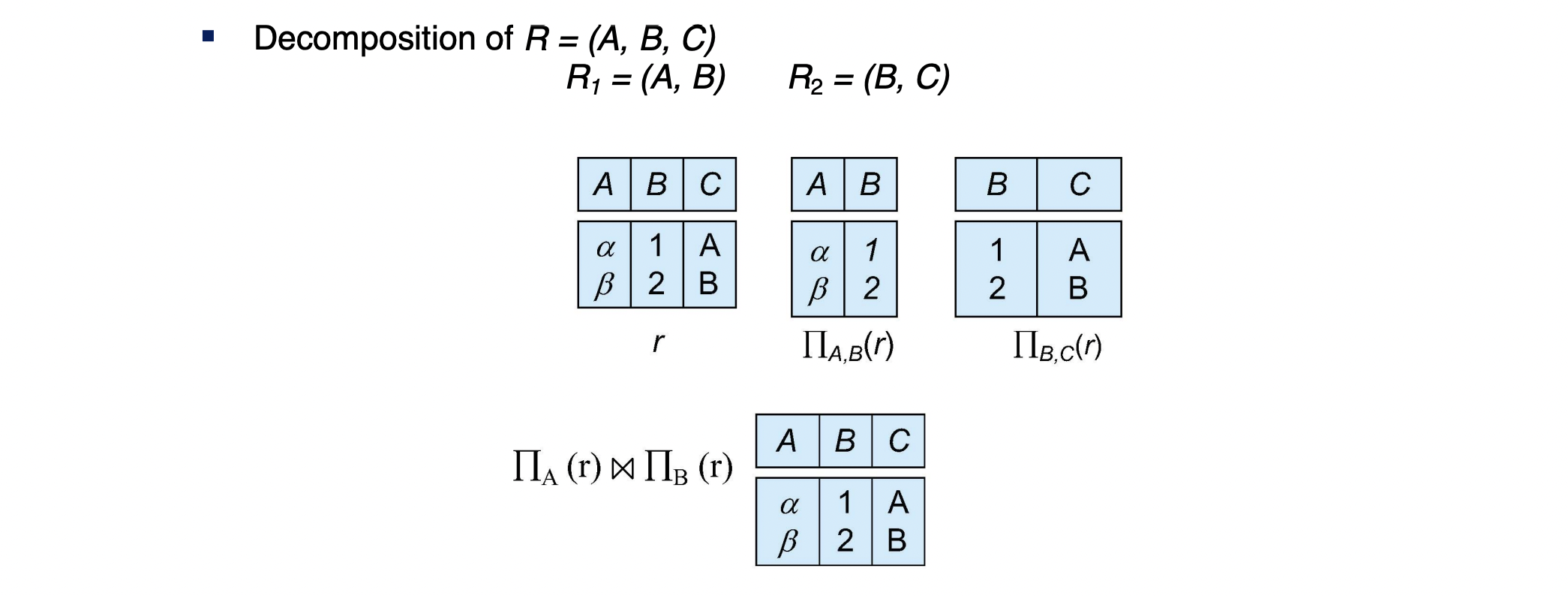
R = (A, B, C)
F = {A->B, B->C}
-
Q1.
R1 = (A, B) and R2 = (B, C)
R1 ∩ R2 = (B)이고,
(B) -> R1 은 만족하지 않는다. B->A가 없기 때문이다
(B) -> R2 는 만족한다. B->B는 trivial하고 B->C가 있기 때문이다
즉, 둘 중 하나를 만족하기 때문에 lossless decomposition이다 -
Q2.
R1 = (A, B) and R2 = (A, C)
R1 ∩ R2 = (A)이고,
(A) -> R1 은 만족한다.
(A) -> R2 는 만족하지 않는다. => F+에서 확인하는 거니까 만족하는 거 아닌가??
즉, 둘 중 하나를 만족하기 때문에 lossless decompoistion이다
Dependency Preservation
- database가 업데이트될 때마다 functional dependency constraint를 test하는 것은 비싸다.
- 그래서 constraint가 효율적으로 test되도록 database를 design하는 것이 좋다.
- functional dependency testing이 하나의 relation만 고려하고 끝날 수 있다면, 비용적으로 아주 좋다.
- When decomposing a relation it is possible that it is no longer possible to do the testing without having to perform a Cartesian Produced.
(decompose할 때, Cartesian 하지 않고 test하는 것이 불가능하게 만들 수 있다) - 2개를 결합해야 dependency를 확인할 수 있고, 각각으로는 dependency를 확인할 수 없는 것을 NOT dependency preserving이라고 한다.
Example
-
dept_advisor(s_ID, i_ID, dept_name)는 다음과 같은 functional dependency가 있다 :
- i_ID -> dept_name
- s_ID, dept_name -> i_ID
-
위 schema는 dept_name이 계속 반복되는 상황을 만든다.
그래서 우리는 decompose할 필요가 있다. -
하지만 어떻게 decompose하든, 두 번째 dependency를 체크하려면 join이 필요하다.
3개의 속성이 다 들어있기 때문이다. -
즉, NOT dependency preserving하다.
-
하지만, lossless하게 잘 쪼갤 수 있다.
R1 = {s_ID, i_ID} and R2 = {i_ID, dept_name}이면,
R1 ∩ R2 = {i_ID}이고, {i_ID} -> R2를 만족한다. -
결국, 좋은 decompose라는 것은
- lossless하고,
- dependency preserving해야 한다.
