BCNF
Boyce-Codd Normal Form ("good form")
- A relation schema R is in BCNF
with respect to a set F of functional dependencies
if for all functional dependencies in of the form å->ß
where a ⊂ R and ß ⊂ R,
at least one of the following holds :- å -> ß is trivial (i.e., ß ⊂ å)
- å is a superkey for R
Example
in_dep (ID, name, salary, dept_name, building, budget)
is NOT in BCNF
Consider a dependency : dept_name -> building, budget
1. trivial하지 않다. (부분집합은 아니다)
2. dept_name이 superkey도 아니다 => superkey가 아닌 이유는??
(ID랑 같이 있어야 primary key 역할을 하기 때문?)
이걸 instructor와 department로 decompose하면,
- instructor is in BCNF
instructor(ID, name, dept_name, salary)
여기서 는 {ID -> name, dept_name, salary}이다.- trivial하지 않다.
- ID는 superkey이다. (primary key는 반드시 superkey)
- department is in BCNF
dept(dept_name, building, budget)
여기서 는 {dept_name -> building, budget}이다.- trivial하지 않다
- dept_name은 superkey이다.
결과적으로 BCNF가 되면 정보의 중복 같은 문제가 발생하지 않는다.
Decomposing into BCNF
-
Let R be a schema that is not in BCNF.
Let å -> ß be the FD(functional dependency) that causes a violation of BCNF -
우리는 R을 다음과 같이 decompose할 수 있다 :
- å ∪ ß
- R - (ß - å)
-
예시로 보는 게 더 쉬울 것 같다
in_dep(ID, name, salary,dept_name, building, budget)은
dept_name -> building, budget 때문에 BCNF가 되지 않는 것을 위에서 확인했다.- 그럼 å = dept_name, ß = building, budget.
- 따라서 다음과 같이 decompose한다
- (dept_name, building, budget)
- (ID, name, salary, dept_name)
-
좀 더 일반적인 예시로 보자
R = (A, B, C)
F = {A -> B, B-> C}, = {A -> B, B -> C, A -> C}
(결과적으로 A가 primary key인 것을 확인할 수 있음.
그럼 B->C 때문에 얘가 BCNF가 아니다.
그럼 이걸 (B, C)랑 (A, B)로 나누면 각각은 BCNF가 되겠지)- R1 = (A, B) and R2 = (B, C)
- Lossless decomposition
- (B) -> R2
- Dependency Preserving
- Lossless decomposition
- R1 = (A, B) and R2 = (A, C)
- Lossless decomposition
- (A) -> R1
- Not dependency preserving
- B->C를 check할 수 없다 without join R1 and R2
- Lossless decomposition
- R1 = (A, B) and R2 = (B, C)
-
이 예시를 왜 준거지..??
BCNF and Dependency Preservation
-
BCNF와 dependency preservation이 항상 동시에 만족하는 것은 아니다.
-
dept_advisor(s_ID, i_ID, dept_name)을 보자.
dependency :- i_ID -> dept_name
- s_ID, dept_name -> i_ID
(여기도 결과적으로 s_ID, dept_name이 primary key인 걸 확인할 수 있음)
-
자자
-
그럼 먼저 얘가 BCNF를 만족하는지 보자
- 두 번째 dependency는 앞에 애가 primary key니까 OK
- 첫 번째는 trivial하지도 않고, superkey도 아니다.
-
그럼 i_ID -> dept_name이 문제인 dependency이므로,
R1(i_ID, dept_name)과, R2(s_ID, i_ID)로 나눌 것이다. -
그럼, BCNF인 두 relaion으로 decompose까지 완료했다.
우리가 확인하고 싶은 건 BCNF와 dependency perservation이 항상 동시에 만족하는지 이다. -
두 번째 dependency를 보면 3개의 attribute이 모두 필요하므로,
decompose한 두 relation에서 check할 수 없다.
따라서 dependency preserving은 만족하지 않는다. -
결과적으로,
BCNF가 DP를 보장하지는 않는다.
- 이게 3rd Normal Form의 Motivation이 된다.
3NF
Third Normal Form
-
A relation schema R is in 3NF
if for all å -> ß in ,
at least one of the following holds :- å -> ß is trivial (i.e., ß ⊂ å)
- å is a superkey for R
- Each attribute A in ß - å is contained a candidate key for R
(each attribute may be in different candidate key)
-
1, 2번째 조건은 BCNF와 동일하다.
즉, 어떤 relation이 BCNF이면, 3NF이다. -
3번째 조건은
BCNF가 dependency preservation을 만족하기 위한 최소한의 완화 조건이라고 할 수 있다.
Example
-
dept_advisor(s_ID, i_ID, dept_name)
with function dependencies :- i_ID -> dept_name
- s_ID, dept_name -> i_ID
-
BCNF 공부할 때 봤듯이,
두 번째는 superkey 조건을 만족해서 OK지만,
첫 번째는 trivial 조건과 superkey 조건을 만족하지 않았다. -
그렇다면 3번째 조건에 대입해보자
ß - å는 dept_name이다.
그리고, 위 relation의 candidate key는
{s_ID, dept_name}과 {s_ID, i_ID}이다. (왜..?)
어쨌든 dept_name을 포함하는 candidate key가 있기 때문에
3번째 조건을 만족한다 -
dept_advisor is in 3NF
Redundancy in 3NF
다음 schema R은 3NF를 만족한다
- R = (J, K, L)
F = {JK -> L, L-> K}- JK->L : 1번은 만족x, 2번 만족. good
- L->K : 1번 만족x, 2번 만족x, 3번 만족.
=> 3NF
| J | L | K |
|---|---|---|
| j1 | l1 | k1 |
| j2 | l1 | k1 |
| j3 | l1 | k1 |
| null | l2 | k2 |
3NF는 만족하지만, 문제가 좀 보인다
- 정보의 중복이 있다. (l1)
- null value를 써야 한다.
(to represent the relationship l2 and k2
where there is no corressponding value for J)
결과적으로, BCNF와 3NF의 장단점을 명확하게 볼 수 있다.
- BCNF : 정보의 중복은 없지만, dependency preserving을 보장하지 못한다
- 3NF : dependency preserving은 보장하지만, 정보의 중복이 발생할 수 있다.
(..? 근데 BCNF면 3NF래매.. 뭐야...필기 잘못했나??)
BCNF vs 3NF
- Advantages to 3NF over BCNF
: It is always possible to obtain a 3NF design without sacrificing losslessness or dependency preservation
- Disadvantages to 3NF
: We may have to use null values to represent some of the possible meaningful relationships among data items.
There is the problem of repetition of information
Goals of Normalization
- Let R be a relation schema with a set F of functional dependencies.
- Decide whether a relation schema R is in "good" form
- In the case that a relation schema R is not in "good" form,
need to decompose it into a set of relation schema {R1, R2, ..., Rn} such that :- Each relation schema is in good form
- The decomposition is a lossless decomposition
- Preferbly, the decomposition should be dependency preserving
How good is BCNF?
There are database schemas in BCNF that do not seem to be sufficiently normalized
- inst_info(ID, child_name, phone) 을 보자.
여기서, 한 명의 instructor는 여러 child_name을 가질 수 있고, 또 여러 phone을 가질 수 있다. 즉 두 속성은 multivalued이다. - 그렇게 되면, 이 관계의 primary key는 (ID, child_name, phone) 전체가 된다.
- 그렇게 되면, dependency는 trivial dependency밖에 없다.
(I, c, p) -> (I, c, p) - 또 그렇게 되면, 얘는 BCNF를 만족한다.
- 아으 근데 뭔가 찜찜하다. 표를 보면 무슨 느낌인지 알겠다.
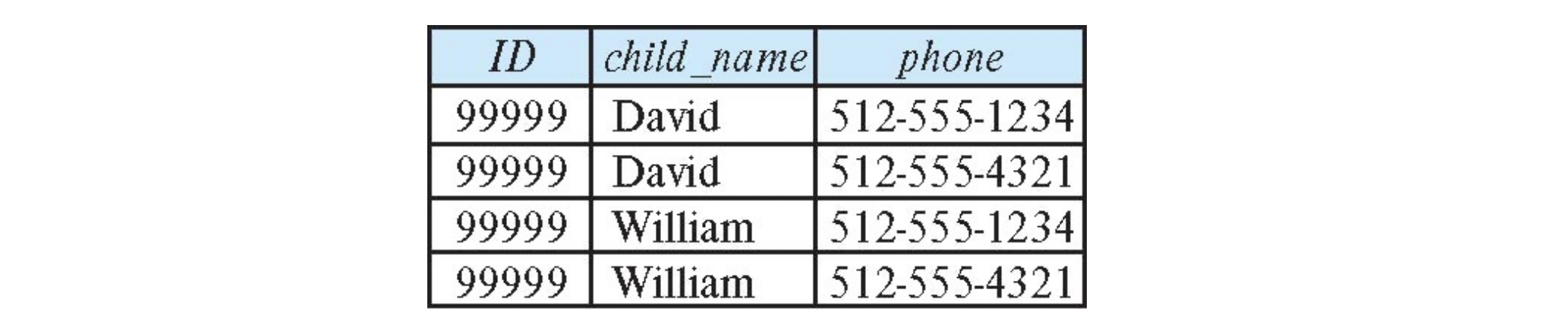
- 여기다 99999가 phone을 하나 더 추가해서, 번호를 하나 더 추가하려고 하면, 우리는 두개의 tuple을 추가해야 한다.
(99999, David, ~~), (99999, Wiliam, ~~)
Higher Normal Forms
- 그래서 우리는 저 inst_info를 더 쪼갠다.
inst_child(ID, child_name) and inst_phone(ID, phone) - 그렇게 되면, 각각은 BCNF를 만족하고 중복은 발생하지 않는다.
- 이건 4NF와 같은 higer normal form의 필요성을 보여준다.
좀 더 나중에 배울 예정이다.