연산 [3].

과학적 표기법 (scientific notation)
: 소수점의 왼쪽에는 한 자리 수만이 나타나게 하는 표기법

정규화된 수 (normalized number)
: 선행하는 0이 없는 부동소수점 표기법으로 나타낸 수
$1.0{ten} * 10^{-9}$

이진수도 이런 방식으로 나타낼 수 있다.
$1.0_{two} * 2^{-1}$

부동소수점(floating point)
: 소수점의 위치가 고정되어 있지 않은 수로 표현하는 컴퓨터 연산

Floating Point Format

S	Exponent	Fraction

$x = (-1)^s * (1 + Fraction) * 2^{Exponent - Bias}$

• S : 부호.
  0이면 양수, 1이면 음수

• Exponent : 지수
  single에서는 8 bit, double에서는 11 bit
  exponent is unsigned
  single에서 bias = 127, double에서 bias = 1023

• Fracition : 소수
  single에서는 23 bit, double에서는 52 bit

• Normalize significand
  1.0 ≤ |significand| ≤ 2.0

-1은
$-1 + 127_{ten}$ 또는
$126_{ten} = 0111 1110_{two}$로 표현한다

+1은
$1 + 127_{ten}$ 또는
$128_{ten} = 1000 0000_{two}$로 표현한다.

---

Single Precision Range

Smallest value

• exponent = 0000 0001
  => actual exponent = 1 - 127 = -126
• fraction : 000...00
  => significand = 1.0
• $\pm1.0 * 2^{-126}$

Largest value

• exponent = 1111 1110
  => actual exponent = 254 - 127 = +127
• fraction : 111...11
  => significand = 2.0
• $\pm2.0 * 2^{+127}$

Example

$Q1. -0.75_{ten}을 binary 부동소수점로 표현해라$

$Q2. 다음 부동소수점을 십진수로 표현해라$

---

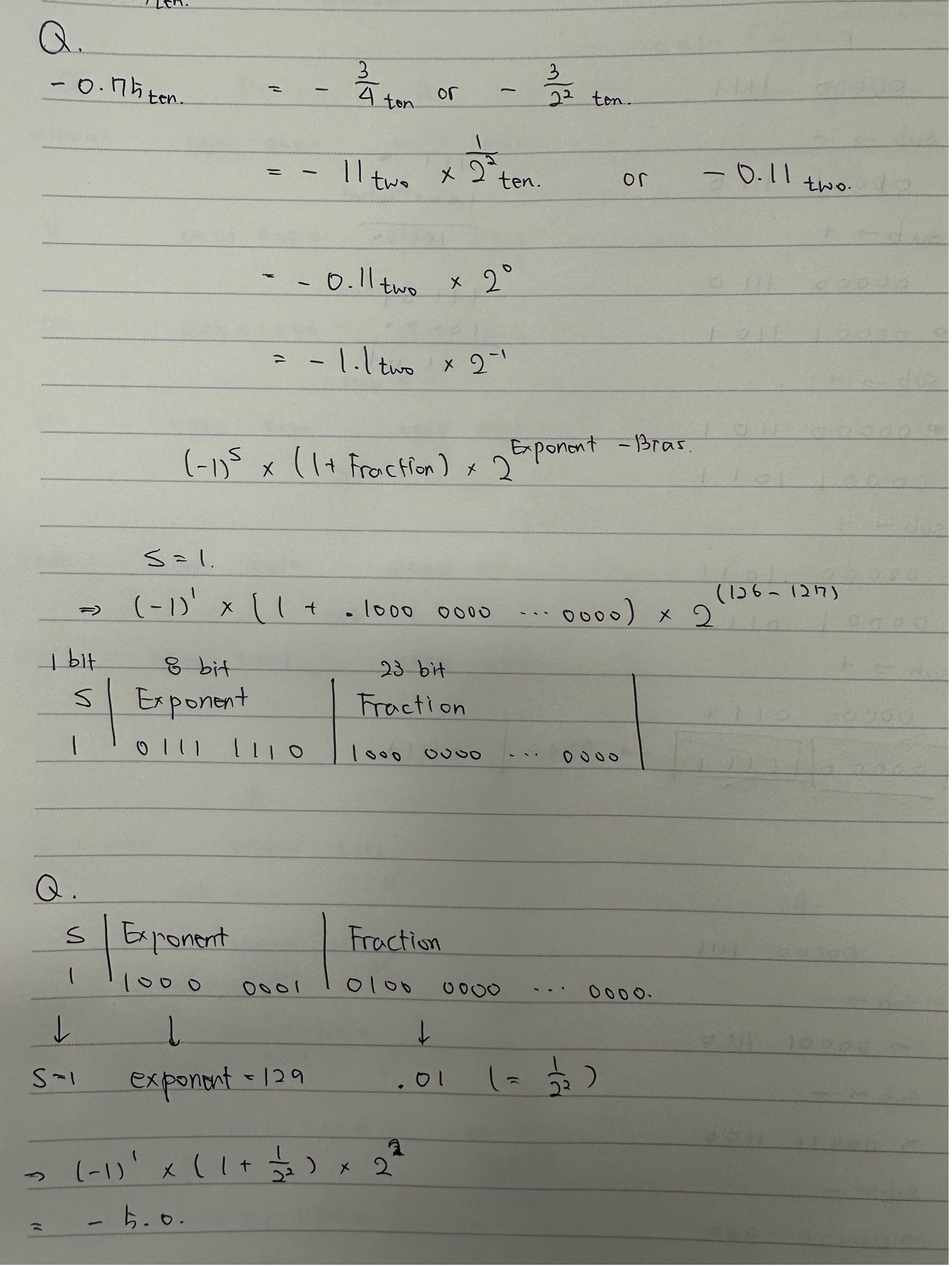
Denormal Numbers

Exponenet = 000...0 => hidden bit is 0
$x = (-1)^S * (0 + Fraction) * 2^{-Bias + 1}$
: smaller than graudal underflow, with diminishing precision

fraction = 000...0
$x = (-1)^S * (0 + 0) * 2^{-Bias}$

Infinities and NaNs

Infinity

Exponent = 111...1, Fraction = 000...0
: $\pm infinity$
: can be used in subsequent calculations,
avoiding need for overflow check

NaN

Exponent = 111...1, Fractino ≠ 000...0
: Not a Number
: indicates illegal or undefined result
(e.g. 0.0 / 0.0)
: can be used in subsequent calculations