Pre-Activation ResNet

Abstract

본 논문에서는 Residual Block의 연산과정에 대해 분석하고 이를 통해 새로운 Residual Block을 고안한다.

Introduction

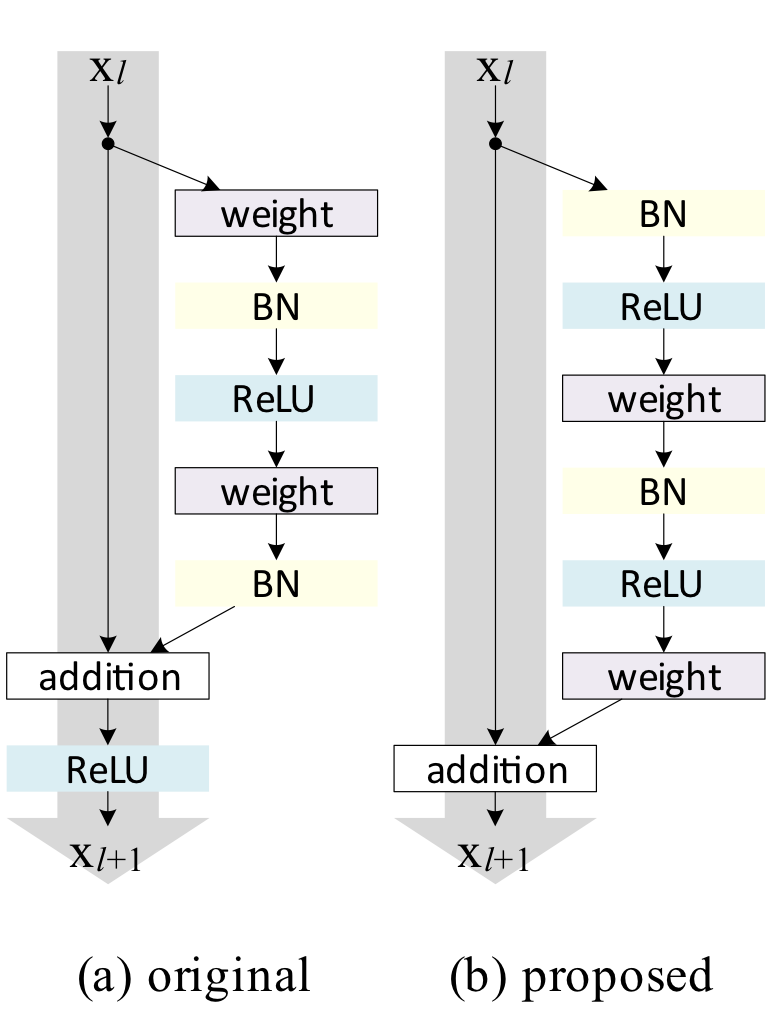
기존의 논문에서는 Fig.1(a)의 residual block을 사용했다. 이를 수식으로 풀어보자

.

$y_l = h(x_l) + F(x_l, W_l)$
$x_l+1 = f(y_l)$

여기서 $h(x_l)$은 identity mapping을 의미하고 $F(x_l, W_l)$은 redisual mapping을 의미한다. 그리고 $f(y_l)$은 ReLU activation을 적용시킨다는 의미이다.

저자의 연구에 따르면 $h(x_l)$과 $f(y_l)$이 identity mapping일 때 forward 방향과 backward방향 모두에서 데이터가 직접적으로 전달된다고 한다. 이 조건을 만족하는 구조가 Fig.1(b)이다.

기존의 상식처럼 여겨졌던 "Activation function은 Weight연산 이후에 적용되어야 한다."는 규칙을 깨버림으로써 학습이 더 잘되고, 일반화도 더 잘되는 결과를 얻은 것이다.

Analysis

위의 식에서 $h(x_l)$이 identity mapping이라면 $h(x_l)=x_l$이고 $f(y_l)$이 identity mapping이라면 $y_l = x_{l+1}$이 된다.
이를 식으로 표현하면 다음과 같다.

.

$x_{l+1} = x_l + F(x_l, W_l)$
$x_L = x_l + \sum_{i=1}^{L-1}F(x_i, W_i)$

이 식에서 중요한 성질을 볼 수 있다.

1. 아무리 L이 깊더라도 모델을 $x_l$과 sigma로 구성된다. 즉 $L$과 $l$의 unit으로 구성된다.

2. 재귀식의 관점으로 볼 경우 $x_L$은 $x_0$와 이전의 모든 residual function의 합으로 볼 수 있다.

back-propagation은 다음과 같이 표현된다.

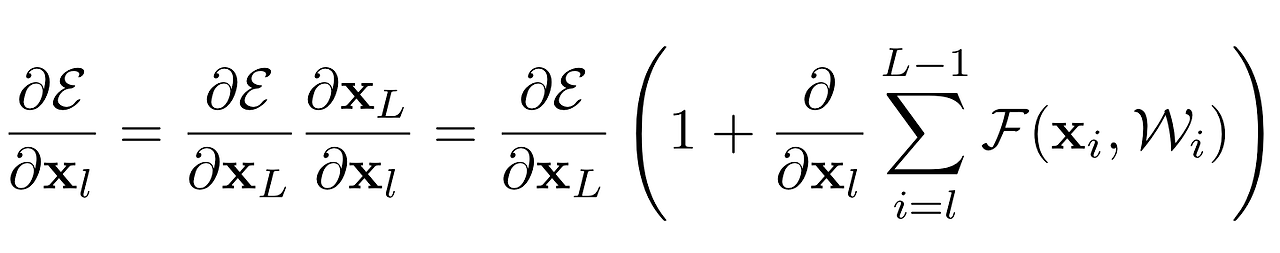
해석

1. 전자 식 : weight layer와는 관계없이 정보를 전달한다.

2. 후자 식 : weight layer를 통해서 정보가 전달된다.

On the Immportance of Identity Skip connections

이 부분에서는 $h(x_l)$이 identity mapping이 아니라면 어떤 결과가 나오는지 보여주는 실험을 했다.

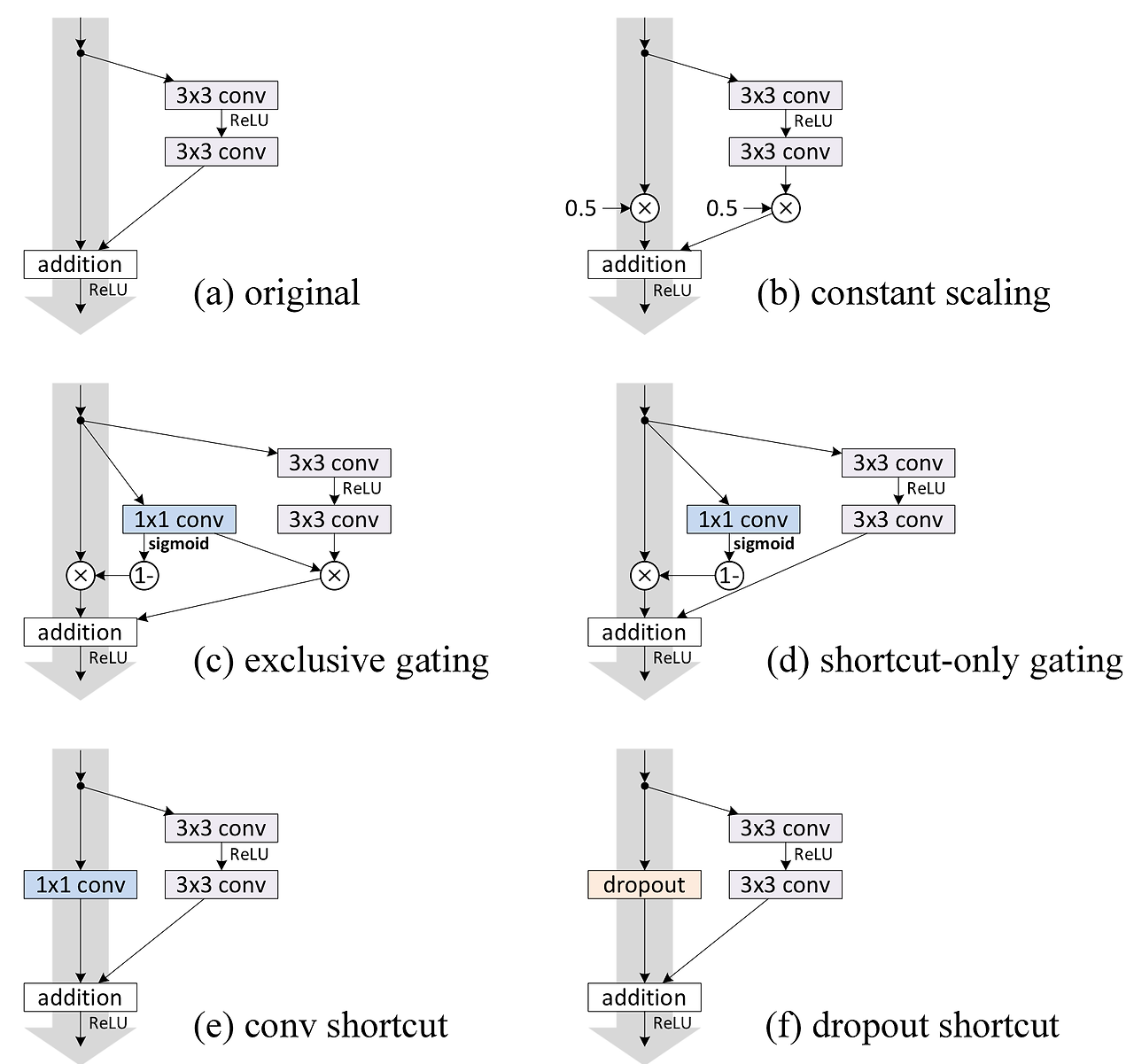
1. Scaling: $h(x_l) = \lambda_l x_l$
   스칼라 값을 input에 곱해주면, back-propagation시 스칼라 값이 중첩되어 곱해진다. 만약 $\lambda_l$값이 1보다 작다면 중첩된 lambda의 곱은 0으로 수렴하여 vanishing gradient문제가 발생하게 되고, 1보다 크다면 lambda의 곱은 발산하여 exploding gradient문제가 발생하게 된다.

2. Exclusive gating
   1x1 conv연산 결과에 softmax를 적용시켜 적절한 비율만큼 residual mapping과 identity mapping에 곱해주는 방식

3. shortcut-only gating
   2번 방식과 유사하지만, residual mapping부분은 softmax출력과 관계없이 그대로 더해진다.

4. 1x1 convolution
   identity mapping을 1x1 conv로 교체한 방식

5. Dropout shortcut
   identity mapping에 dropout을 0.5만큼 적용시키는 방식이다. 이는 Scalar를 0.5로 둔것과 유사하게 볼 수 있다.

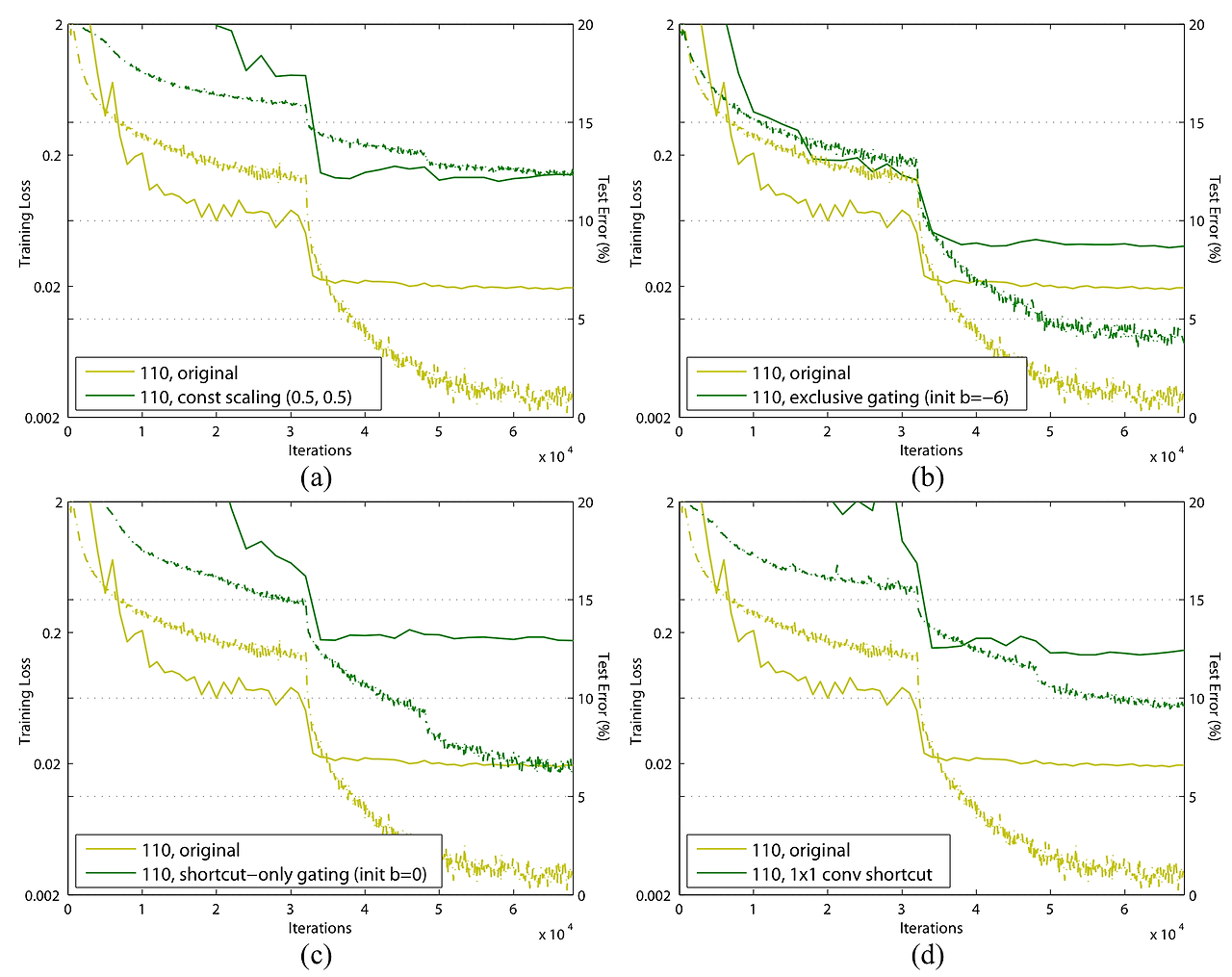
성능은 모든 기존의 residual net보다 좋지 않았다.

On the Usage of Activation Functions

이 부분에서는 $f(y_l)$이 identity mapping이 아니면 어떤 결과를 낳는지에 대한 실험을 진행한다.

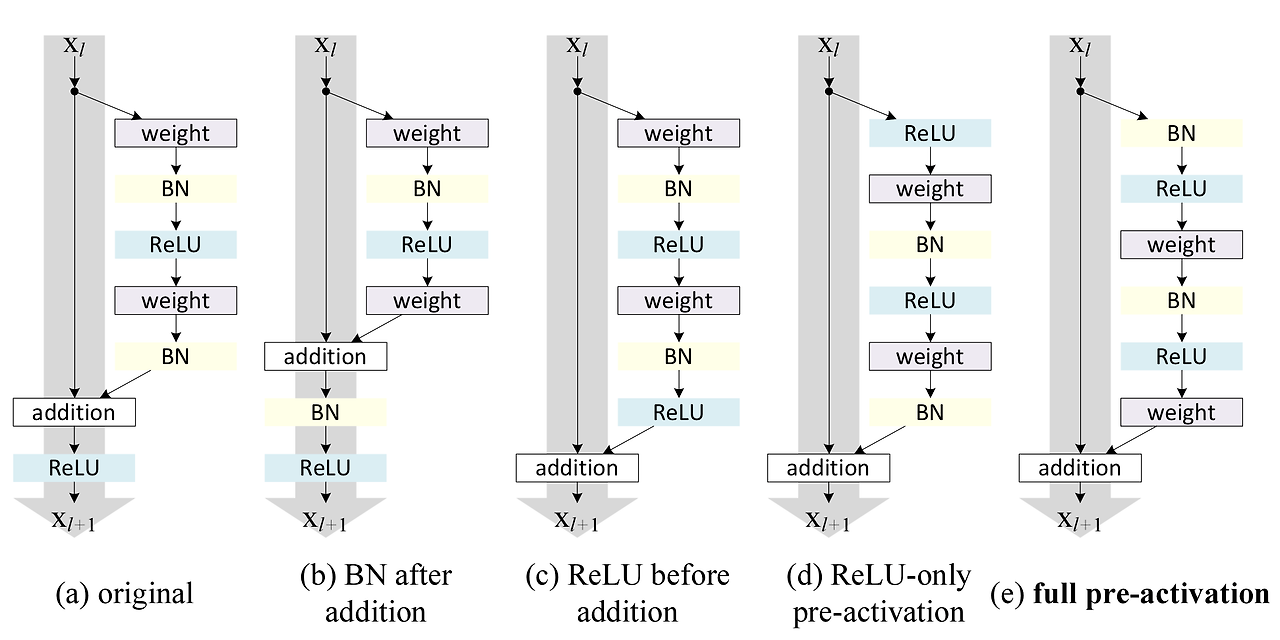
1. BN after addition
   기존의 방식에서 BN을 더한 이후에 놓은 방식이다. original보다 성능이 떨어진다고 한다.

2. ReLU before addition
   ReLU를 residual mapping 안에 집어넣었다. 이때 residual mapping의 output의 범위가 [0, $\infin$]이 되기 때문에 layer를 거칠수록 값이 커진다는 문제가 있다.

3. ReLU-only pre-activation
   2번의 문제점을 해결하기 위해 ReLU를 뒤로 옮겼다. 하지만 BN의 효과를 누리지 못함

4. full pre-activation
   3번의 단점을 해결하기 위해 BN까지 뒤로 옮겼다.

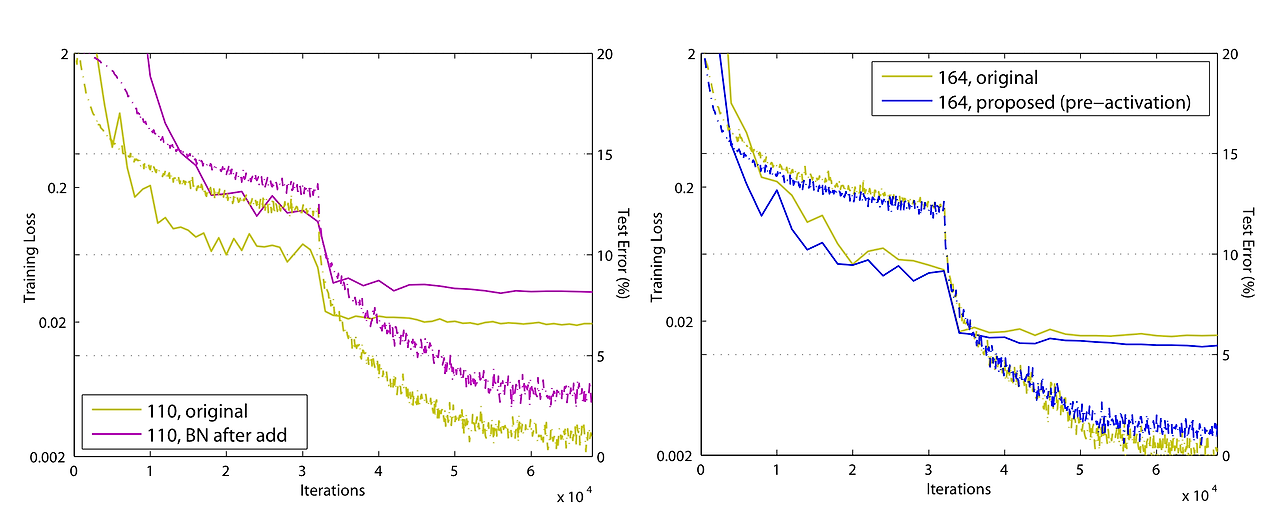
2번방식은 기존보다 성능이 좋지 않았고, 4번 방식을 사용했을때 기존 방식과 비슷한 성능을 보였다.

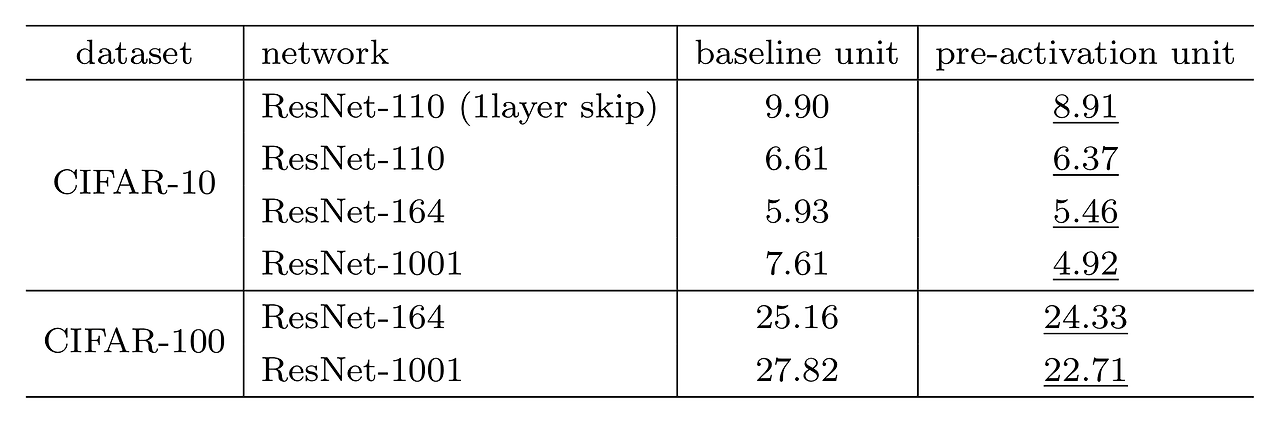
하지만 ResNet은 layer깊이를 1001개로 늘렸을때, Overfitting이 발생한 반면 pre-activation은 Overfitting이 발생하지 않았다고 한다.

그 이유로 저자는 기존의 ResNet에서는 Weight Layer의 입력이 unnormalize상태이지만 (BN이 먼저 적용되지 않았으므로), pre-activation에서는 normalize된 상태 (BN이 먼저 적용되었기 때문에)이기 때문일 것이라고 추측하였다.

결과적으로는 BN으로 overfitting을 막은 거라고 볼 수도 있을 것 같다.

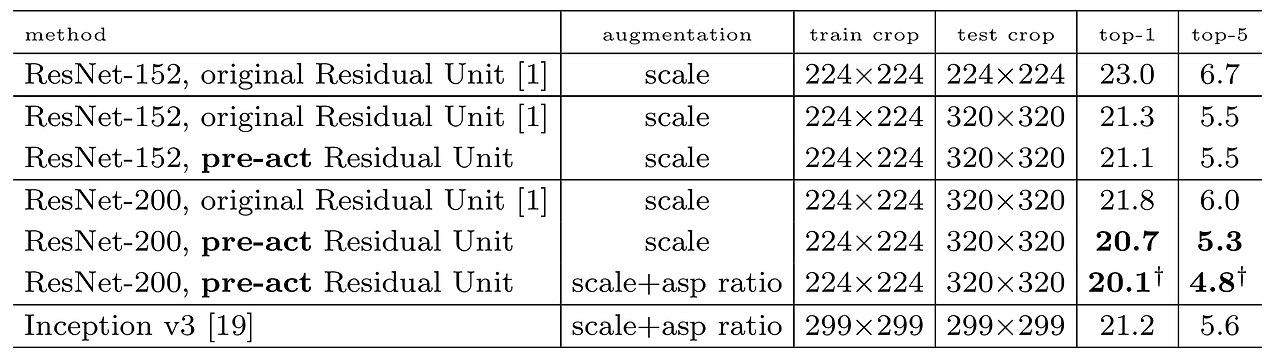
Pre-activation ResNet은 top-1 error를 20.1%, top-5 error를 4.8%로 기록하면서 기존의 ResNet의 성능을 앞섰고, Inception V3도 앞선 결과를 보여주었다.