
03-1 k-최근접 이웃 회귀
지도 학습 알고리즘 이렇게 두가지로 나뉘어진다.
-분류
-회귀
회귀란?
샘플을 바탕으로 임의의 어떤 숫자를 예측하고자 하는 알고리즘
그럼 예측이라고 하면 되지 왜 회귀라고 했을까는 사족
k-최근접 이웃 분류와 k-최근접 이웃 회귀의 차이
- 분류
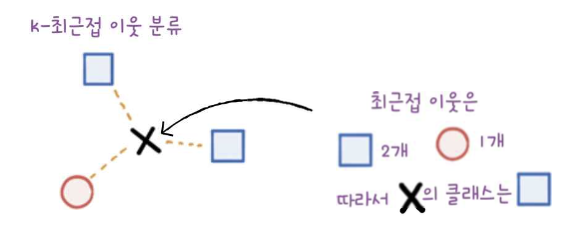
- 회귀
데이터 준비
우선 농어의 길이를 특성, 무게를 타깃이라고 하고 훈련을 위해 train_test_split() 함수를 이용한다.
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight)여기서 중요한 점은 사이킷런에서 훈련 세트는 2차원 배열이여야 하는데, 지금 구한 건 1차원 배열이란 것이다. 1차원 배열을 2차원 배열로 바꾸는 방법은 열 하나를 추가하는 것이다.

이렇게. 파이썬에서 1차원 배열의 크기는 원소가 1개인 튜플로 나타내고 크기는 reshape(3,1)과 같이 바꿀 수 있다. 귀찮으면 reshape(-1,1)도 가능한데 -1은 나머지 원소 갯수로 모두 채우라는 것을 의미한다.
이는 열의 값은 특정 정수로 지정이 되어있을 때, 남은 배열의 길이와 남은 차원으로부터 추정해서 알아서 지정하라는 의미입니다.
-1의 의미가 이해가 안된다면 여길 클릭
밑의 이미지는 별개의 내용인데 reshape를 하면 어떤 식으로 숫자를 잘라서 구겨 넣는지 궁금해서 해봤다. 열 기준으로 잘 잘라 넣는가보다.
그리고 하면서 깨달았는데 reshape는 sorted처럼 원본에 영향을 안미치는 함수이다. 그래서 변형시킨 걸 원본에 적용시키고 싶으면 arr = arr.reshape(2,2)이렇게 다시 써줘야한다.
결정계수(R^2)
준비한 데이터로 KNeighborsRegressor() 클래스를 활용하여 fit하면 된다.
결정계수 : coefficient of determination
결정계수는 회귀에서의 스코어이다.
분류에서의 스코어는 정답을 맞춘 비율이 되지만 회귀에서의 스코어는 예측한 것이 타깃에 가깝냐 평균에 가깝냐가 된다.
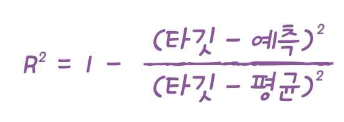
즉, 예측이 타깃에 가까우면 분자가 커져 1에 가까워지고, 예측이 평균에 가까우면 분모가 커져 0에 가까워진다.
예측이 평균과 얼마나 차이가 나는지 정확하게 알고 싶다면 다음의 코드를 참고하면 된다.
'타깃과 예측의 절댓값 오차'의 평균
from sklearn.metrics import mean_absolute_error
test_prediction = knr.predict(test_input)
mae = mean_absolute_error(test_target, test_prediction)
print(mae)19g 정도 차이가 남을 확인할 수 있었다.
과대적합 vs 과소적합
과대 적합 : 훈련 세트만 과도하게 스코어가 높은 경우
과소 적합 : 둘 다 낮거나 테스트 세트만 스코어가 높은 경우
과대 적합의 경우 원인 예시
- 데이터 세트 내 데이터가 충분하지 못한 경우
- 데이터 세트 내 분산이 크거나 노이즈가 큰 경우 (이 경우 노이즈까지 학습해버림)
과소 적합의 경우 원인 예시 - 모델이 너무 단순하여 훈련 세트에 적절히 훈련되지 않는 경우
- 데이터 세트 내 데이터가 충분하지 못한 경우
지금 예제의 문제는 과소적합이기 때문에 k-최근접 이웃 회귀 알고리즘에서는k_neighbors의 값을 작게 해주면 국지적으로 판단하여 조금 더 복잡성을 주어 훈련 세트에 맞게 훈련될 수 있다.
반대의 경우에는 이웃의 값을 크게 해주면 된다
03-2 선형 회귀
k-최근접 이웃 회귀 알고리즘을 쓰면 훈련 세트에 비해 너무 벗어나는 데이터는 이상하게 판단한다...
그야 당연히 주변의 3개쯤의 평균 값을 계산해서 예측하는 것이기 때문이다.
그것의 해결법!!! 선형 회귀에 대해 소개한다.
선형 회귀
sklearn.linear_model 패키지에 LinearRegression 클래스를 활용해서 만들 수 있다.
선형회귀 알고리즘을 사용해서 얻어진 직선에는 절편이 있다. 그것은 각각 lr 객체의 coef_와 intercept_ 속성에 저장되어 있다.
coefficient = 계수
intercept = 절편
print(lr.coef_, lr.intercept_)이런 계수와 절편을 머신러닝 알고리즘이 찾은 값이란 의미로 model parameter라고 부른다. 앞으로의 많은 머신러닝 알고리즘의 훈련과정은 이런 모델 파라미터를 찾아나가는 여정인 것이다. 참고로 k-최근접 이웃 알고리즘에는 그런 것 없다. 사례기반학습
다항회귀 polynomial regression
선형회귀로는 완전히 맞는 그래프가 아니어서 예측이 어려웠다. 다항회귀로 가보자.
np.column_stack((train_input **2, train_input))의 함수로 2차 방정식에 쓰일 훈련세트를 만들고 테스트 세트도 동일하게 만든다.
그리고 훈련 시키면 이차 함수의 a,b,c(절편)들이 모두 나온다.
이를 바탕으로 이차 함수를 그릴려면 matplotlib의 plot함수를 x를 1로 쪼개서 짧을 직선을 연결연결해서 그리면 된다.
2차 방정식도 선형 회귀인가요?
맞다. 길이`**2도 결국 왕길이라는 변수이다. 그럼 길이와 왕길이가 무게에 대한 선형 회귀를 할 수 있다.
point = np.arange(15, 50)
plt.scatter(train_input, train_target)
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)
plt.scatter([50],[1574], marker='^')
plt.show()여기서 plot 함수의 메소드는 x값이랑 y값이다.
03-3 특성 공학과 규제
PolynomialFeatures 클래스를 이용해 특성이 많은 선형 회귀를 편하게 진행해보자.
다중회귀
다중회귀 : 여러 개의 특성을 사용한 선형 회귀
특성공학 feature engineering : 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업
제곱한 것, 두개를 곱한 것, 그리고 나머지 특성들... 이런 모든 특성을 활용하면 어떻게 될지 궁금하지 않나?? 해보자!
데이터 준비
판다스 : 데이터 분석 라이브러리
데이터프레임 : 판다스의 핵심 데이터 구조
column_stack 같은 함수로 일일히 쌓기 보다는 있는 csv활용해서 df 만들자.
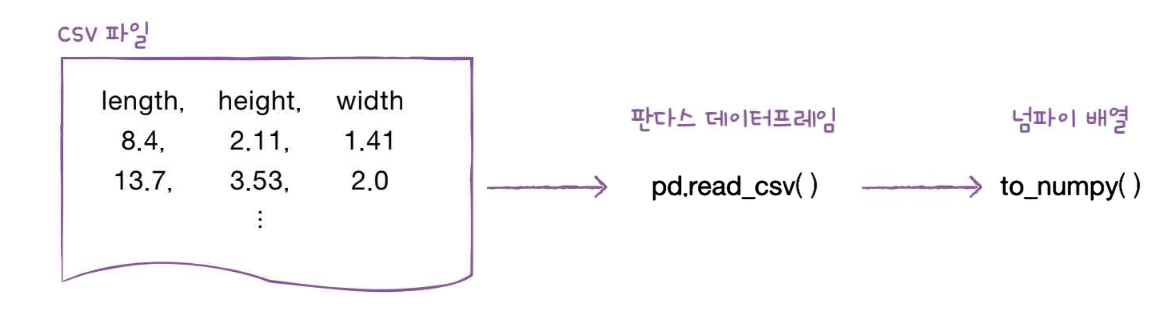
데이터 준비는 train_test_split으로 마무리한다.
사이킷런의 변환기 transformer
transformer : 특성을 만들거나 전처리 하는 클래스
poly = PolynomialFeatures(include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)이 transform으로 만든 train_poly를 선형회귀에 사용하면 된다.
다중 회귀 모델 훈련하기
lr.fit(train_poly, train_target)으로 훈련하면 거의 완벽해진다. 특성이 더 많게 하려면 PolynomialFeatures(degree=5)라는 값으로 설정하면 되지만 그럼 초초초초 과대적합이 되어서 안된다.
규제 regularization
모델이 너무 과대 적합되지 않게 훼방을 놓는 일.
선형 회귀 모델에서는 특성의 계수의 크기를 작게 하는 일이다.
규제 하기 전에 전처리 하자. 특성 간에 천차만별인 규제가 들어가면 안되므로 표준점수화 시키는 것이다.
이번에는 StandardScaler = 변환기 사용할 것.
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)릿지 회귀와 리쏘 회귀
릿지 회귀와 리쏘 회귀의 alpha값을 조절하면서 규제를 조절할 수 있다.
alpha값이 크면 규제 강도 업!
alpha값이 작으면 규제 강도 다운...
강도가 업되면 조금더 과소적합될 수 있다.
