1. Introduction

1) Frontend Structure

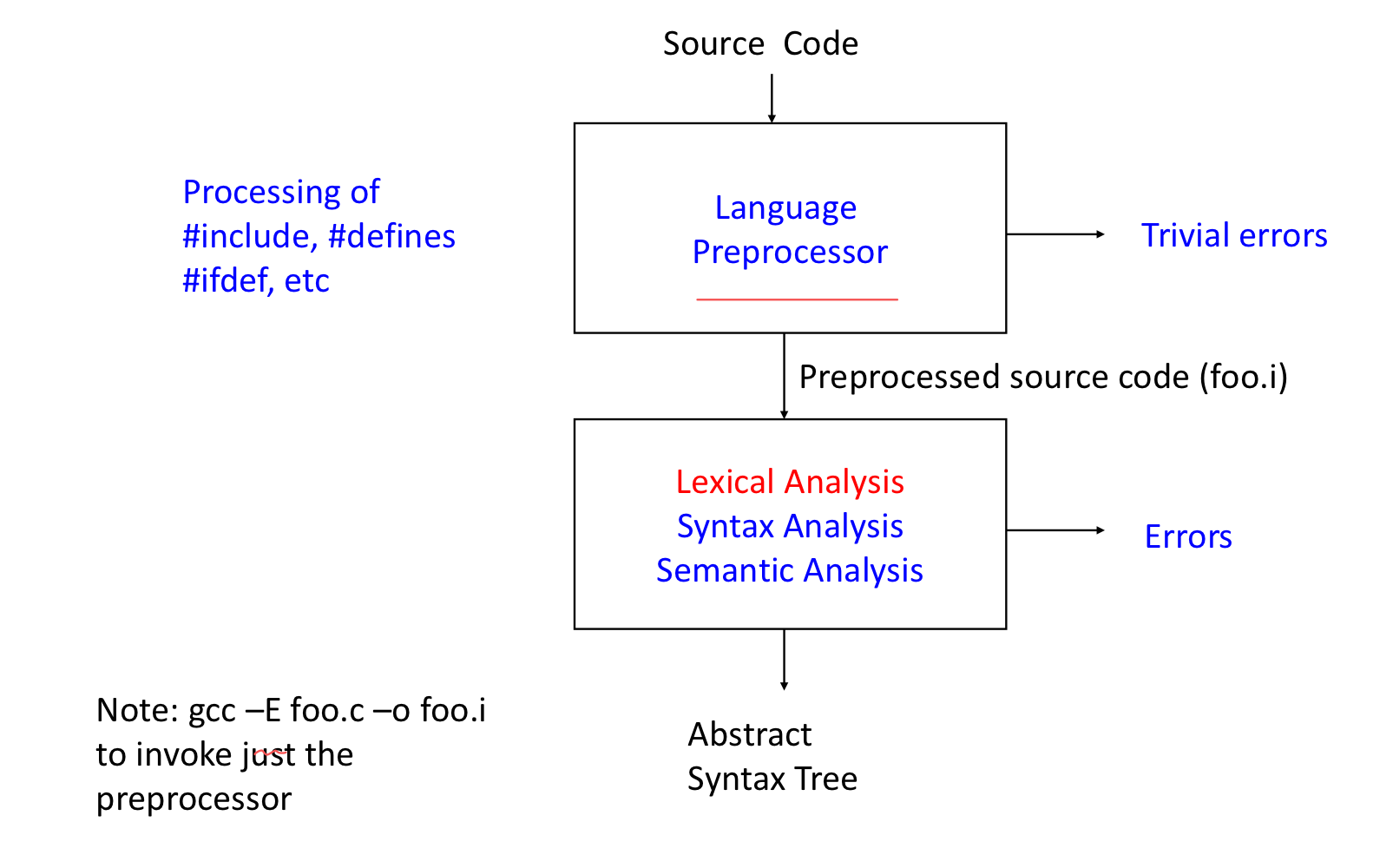
2) Lexical Analysis: Specification, Recognize, and Automata

• Specification: 어떻게 lexical pattern들을 규정할 것인가?

  • In C, identifier들은 x, xy, match0, _abc같은 string들이다.

  • 3, 12, 0.012 and 3.5E4같은 string들은 Number이다.

    → regular expressions (정규표현식으로 maching되는 것을 token으로 만들어준다.)

• Recognition: 어떻게 lexical pattern들을 인식할 것인가?

  • Recognize match0 as an identifier.

  • Recognize 512 as a number.

    → DFA

• Automation: 어떻게 자동으로 specifications에서 string들을 생성할 것인가? → Thompson’s construction and subset construction
  

2. Scanning: introduction

• Scanning or lexical analysis
  • Characters → Tokens
• Tokens
  • 자연어에서 단어 같은 것이다.
  • Examples
    • Keywords: if, while
    • Identifiers
    • Special symbols: +, *, ≥ , …
• pattern matching의 특별한 경우이다.
  • regular expressions: 패턴을 나타내는 표준 표기법이다.
  • finite automata: pattern을 인식하는 algorithm들이다.

a) The scanning process

• a[index ] = 4 + 2 → a / [ / index / ] / = / 4 / + / 2
  

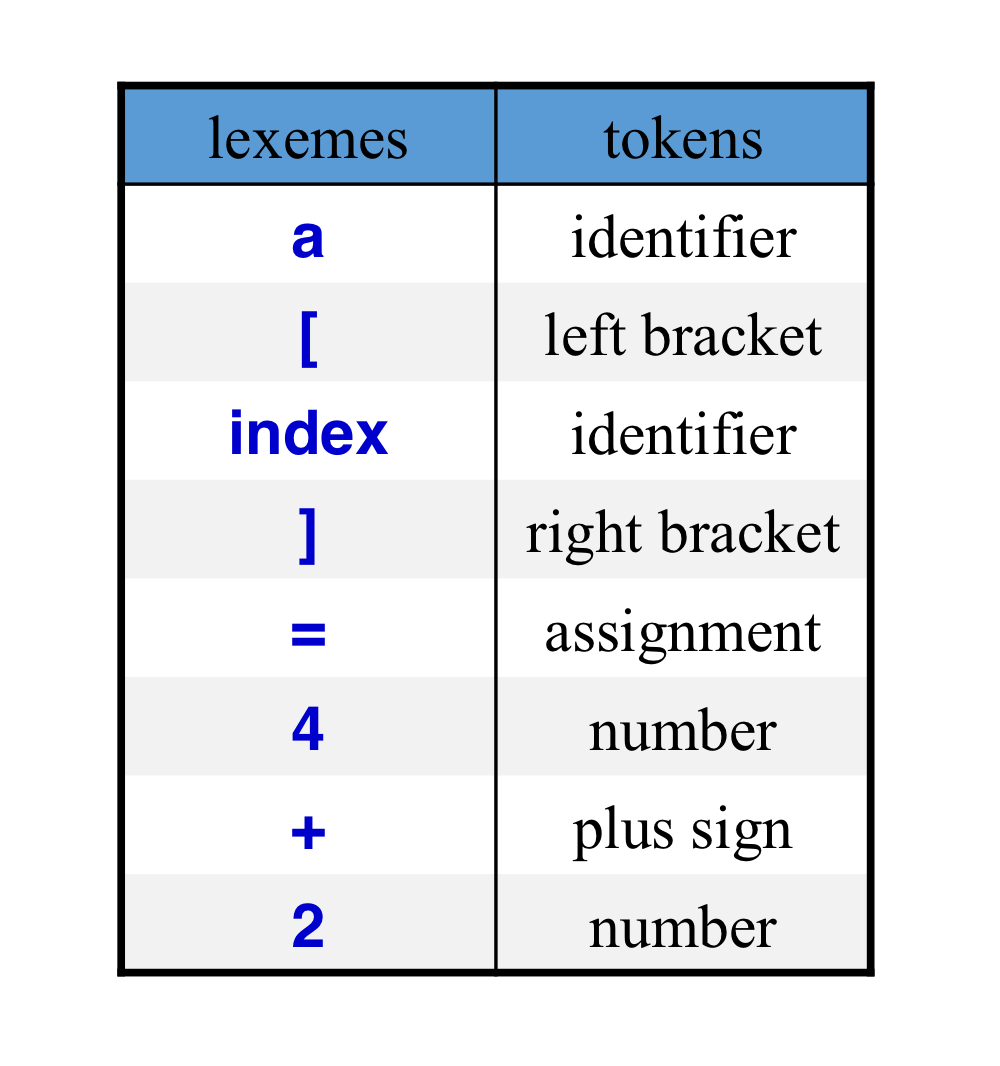
b) Lexical Analysis Process

• Lexical Analysis
  • multi-character input stream을 token stream으로 변환하는 것이다.
  • program 표현의 길이를 줄이는 것이다. (remove spaces)

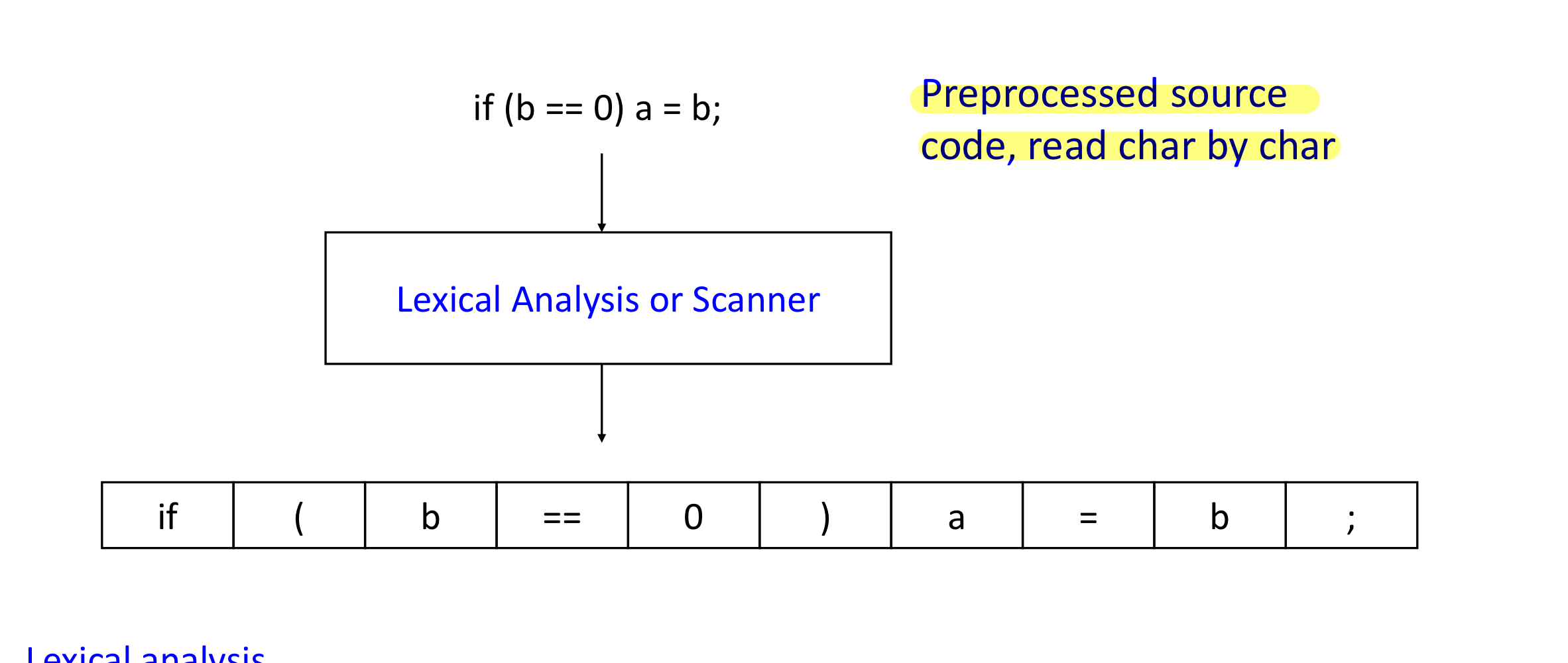
c) The scanning process

• Scanning and parsing은 같이 섞여 있다.
  • TokenType getToken(void)
  • 이 함수는 next token을 하나 씩 return한다.

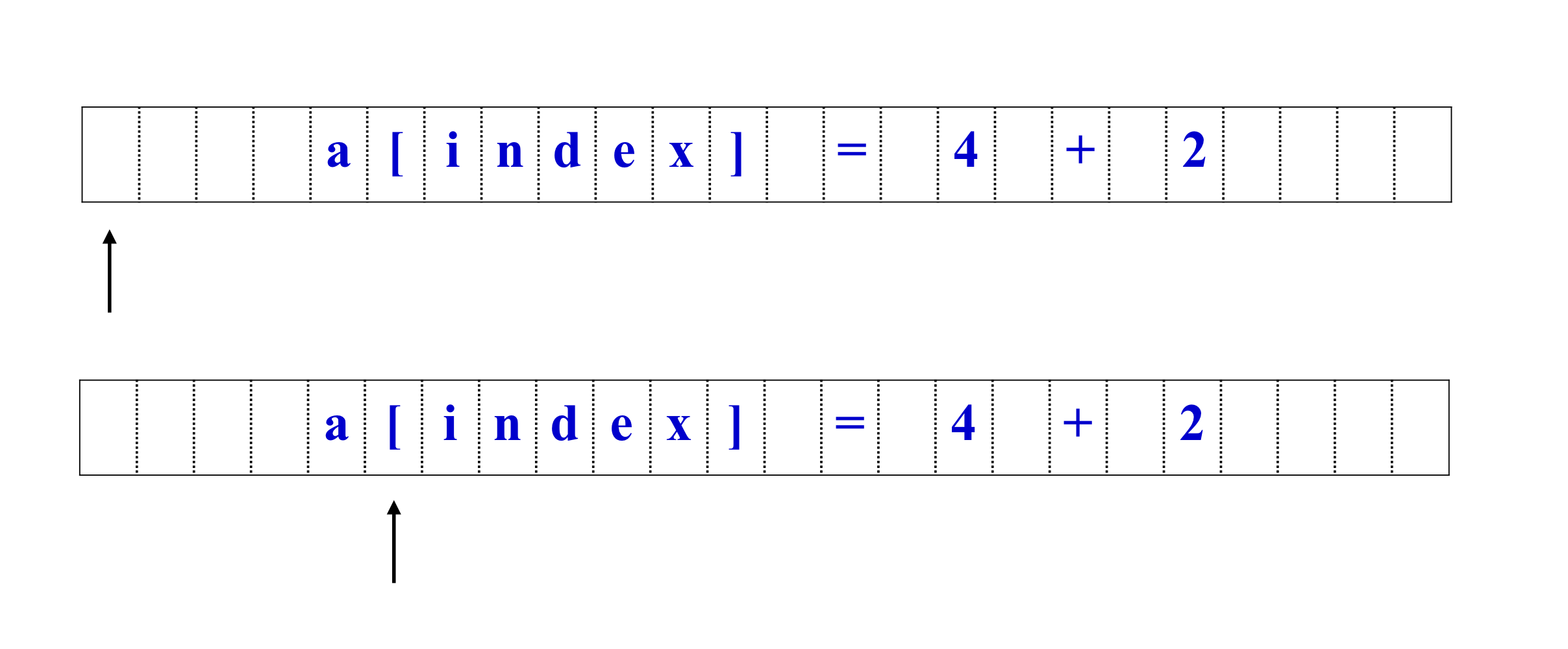
d) Tokens

• Idenetifiers: x y11 elsex
• Keywords: if else while for break
• Integers: 2 1000 -20
• Floating-point: 2.0 -0.0010 .02 1e5
• Symbols: + * {} ++ << < ≤ [ ]
• Strings: “x” “He said, \”I luv compiler\””

2) How to Describe Tokens

• programming language tokens를 구성하기 위해서 regular expressing을 사용한다.
• A regular expression (RE) 는 점진적으로 구성된다.
  • a → ordinary character stands for itself
  • 람다 → empty string
  • R|S → either R or S (alteration), where R,S = RE
  • RS → R followed by S (concatenation)
  • R* → concatenation of R, 0 or more times

a) Language

• regular expression R은 L(R)로 쓰여지는 string들의 집합이다.
• L(R) = the language defined by R
  • L(abc) = {abc}
  • L(hello|goodbye) = {hello, goodbye}
  • L(1(0|1)*) = 1로 시작하는 모든 이진수
• 각 토큰은 regular expression을 사용하여 정의된다.

b) RE Notational Shorthand

• R+ → one or more strings of R: R(R*)
• R? → optional R : (R|람다)
• [abcd] → 이 문자 중 하나: (a|b|c|d)
• [a-z] → 이 범위 문자 중 하나: (a|b|c|d…|z)
• [^ab] → a나 b가 없다.
• [^a-z] → 이 범위 중 하나가 없다.

c) Example

3) Regular expressions

• Definitions
  • symbols: characters
    • a, b, c, +, -, …
  • alphabet: set of legal symbols
    • {A, B, C, …, Z, a, b, c, … ,z}
  • strings: concatenation of symbols
    • I am a boy
• regular expression r은 나타낸다.
  • language L(r)로 생성 된 string들의 집합
• A symbol은 regular exp가 될 수 있다.
  • a: L(a) = {a}, b: L(b) = {b}, …
  • 람다: L(람다) = {람다}, 공집합: L(공집합) = {}
• regular exps들 중 Choice하는 것은 regular exp이다.
  • r|s: L(r|s) = L(r) 합집합 L(s)
  • expample
    • L(a|b) = {a} 합집합 {b} = {a,b}
    • L(a|b|c|d) = {a,b,c,d}
• regular exps들의 Concatenation은 Concatenation이다.

  • rs: L(rs) = L(r)L(s)

    example) L(ab) = {ab}

• regular exp의 Repetition은 regular exp이다.

  • r: L(r) = {람다} 합집합 L(r) 합집합 L(rr) 합집합 L(rrr) …

    example) L(a*) = {람다, a, aa, aaa, … }

  • L(a) = L(a)

    • L((a|bb)) = L(a|bb)
• Futher examples
  • (a|b)c
    • L((a|b)c) = L(a|b)L(c) = {a, b}{c} = {ac, bc}
  • (a|bb)*
    • L((a|bb)*) = {람다, a, bb, aa, abb, bba ,bbbb , …}
• Operation들의 우선 순위

  • • . > |

  • a|bc: L(a|bc) = L(a) 합집합 L(b)L(c)*
• Names
  • (0|1|2|…|9)(0|1|2|…|9)*
  • 이것은 digit digit*로 다시 쓰일 수 있다. (digit = 0|1|2|…|9.)

a) Examples

• {a, b, c}을 alphabet으로 갖는데, 정확하게 하나의 b만 갖는 string의 집합
  • (a|c)b(a|c)
• {a, b, c}를 alphabet으로 갖는데, 많아 보았자 하나의 b를 갖는 string의 집합
  • (a|c)|(a|c)b(a|c)*
  • (a|c)(b|람다)(a|c)
• {a,b}중에 같은 a의 개수로 둘러 싸여져 있는 하나의 b를 갖는 string의 집합
  • {b, aba, aabaa, …}
  • 표현이 불가능 하다.
• Consider the strings over the alphabet ∑ = {a, b, c} that contain no two consecutive b’s.
  • (a|c)(b(a|c))(a|c)*
• Consider the alphabet ∑ = {a, b, c} and the regular expression

  • ((b|c)a(b|c)a)(b|c)

    → a의 개수가 짝수인 regular expression

b) Extensions to regular expressions

• +: one or more repetitions
  • r+ = rr*
  • (0|1|2|…|9)(0|1|2|…|9)* → (0|1|2|…|9)+
• .: any symbol in the alphabet
  • .b.
• -: a range of symbols
  • a|b|c → [abc]
  • a|b|…|z → [a-z]
  • [a-zA-Z]
• ~, ^: 주어진 집합에 포함되지 않는 어떤 기호,
  • ~(a|b|c) or [^abc]: a characer, a또는 b또는 c가 아닌.
• ?: optional subexpressions
  • natural = [0-9]+
  • signedNatural = natural | +natural | -natural → signedNatural = (+|-)?natural
    

c) Regular expressions for PL tokens

• Reserved words
  • reserved = if | while | do | …
• Special symbols
  • +, =, :=, ++ ,…
• Identifiers
  • letter = [a-zA-Z]
  • digit = [0-9]
  • identifier = letter(letter|digit)*
• Numbers
  • nat = [0-9]+
  • signedNat = (+|-)?nat
  • number = signedNat(”.” nat)? (E signedNat)?
• Comments
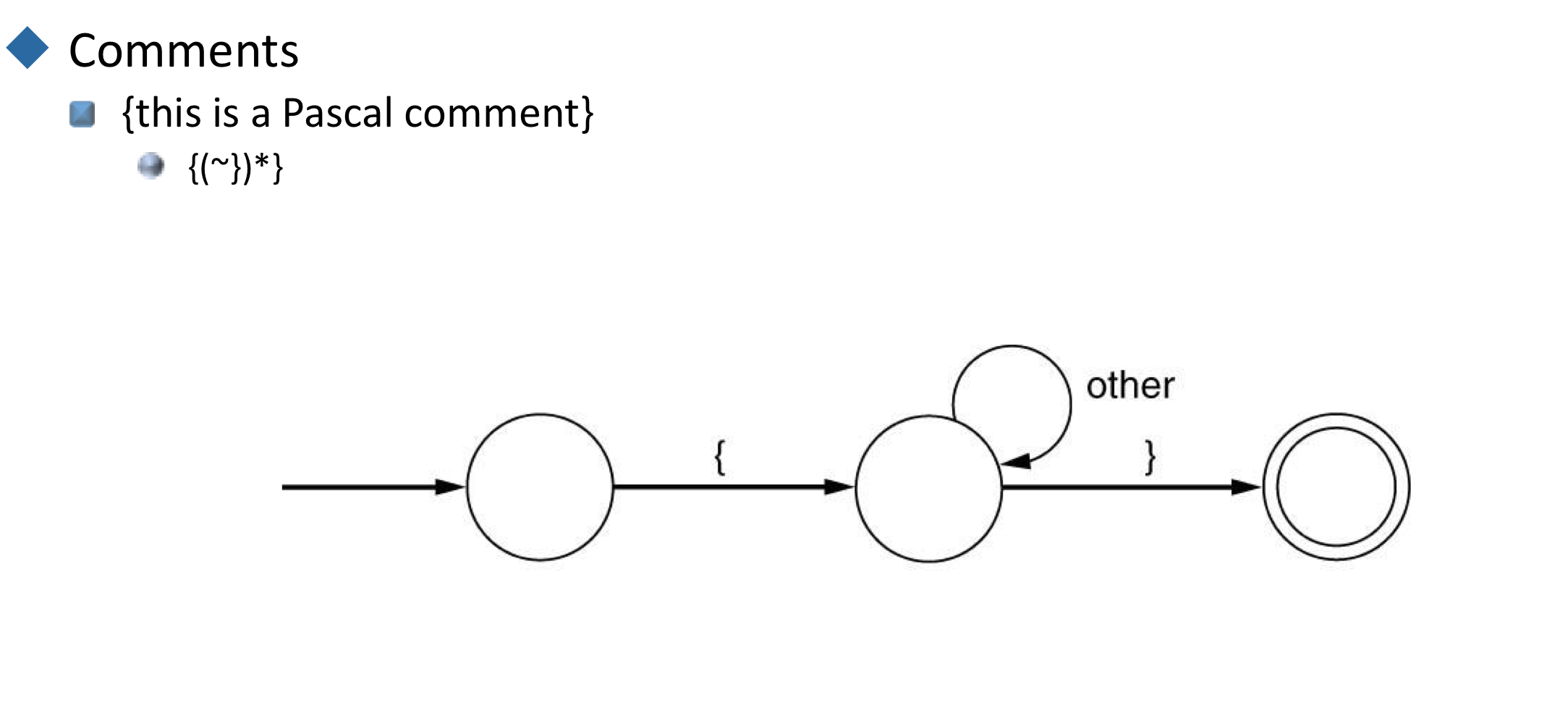
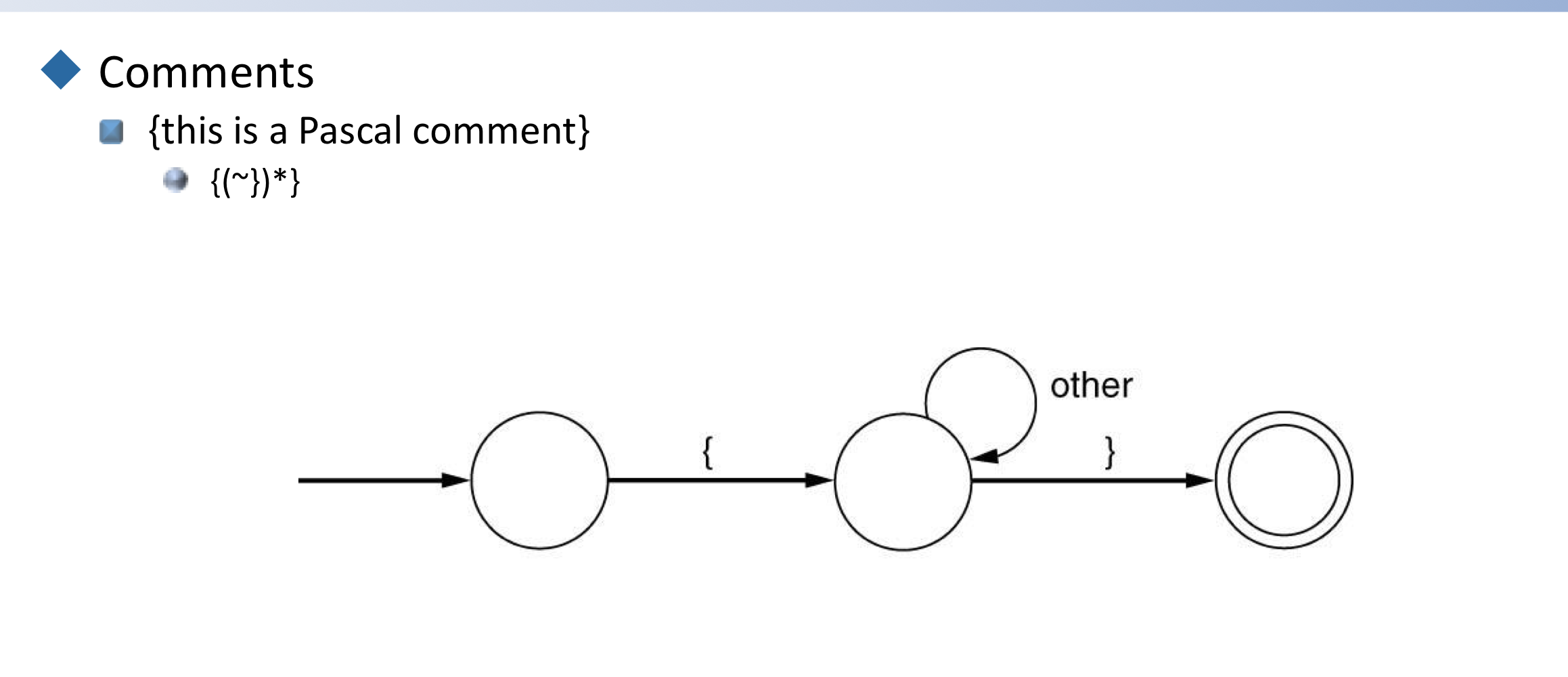
  • {this is a Pascal comment}

    • {(~})*}

      → {가 왔다면, }가 아닌 모든 것을 accept하고 }

  • — this is an Ada comment

    • —(~newline)*

      → —가 왔다면, newline이 아닌 모든 것을 accpet

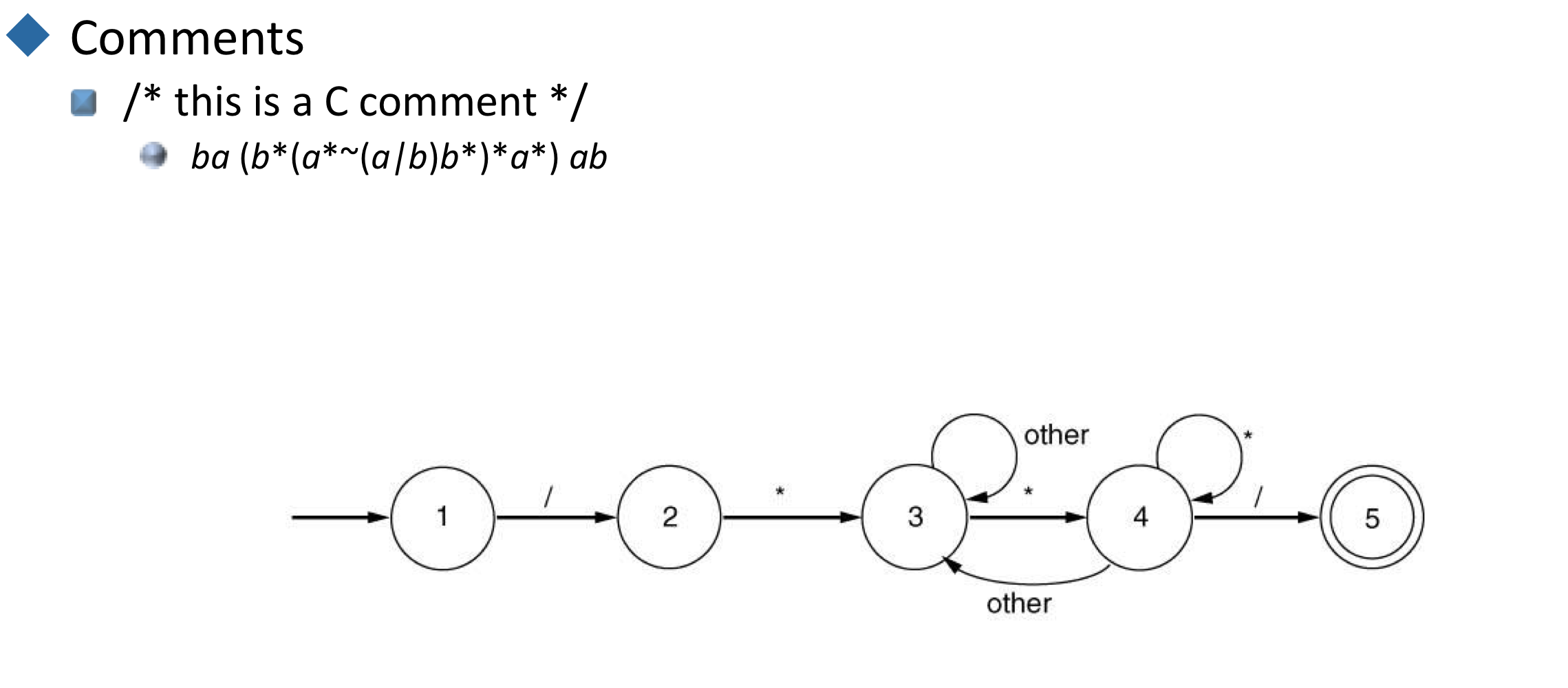
  • / this is a C comment /
    • ba … ab where b = / and a = *.
    • ba(b(a~(a|b)b)a*)ab
    • 복잡해서 보통은 hoc method를 사용해서 다루어진다.
• Ambiguity
  • If는 keyword인가 identifier인가?
  • temp는 identifier temp인가 identifiers te 와 mp인가?
• Disambiguating rules
  • Keyword는 identifier보다 더 우선순위가 높다.
    • if is a keyword
  • 가장 긴 substring이 원칙이다.
    • temp is a identifier temp
• Token delimiters
  • White space
    • whitespace = (blank | tab | newline | comment)+
    • do if, do/**/if
  • 명백히 다른 token의 부분일 때,

    • xtemp=ytemp

      (=는 identifier에 속하지 않기에)

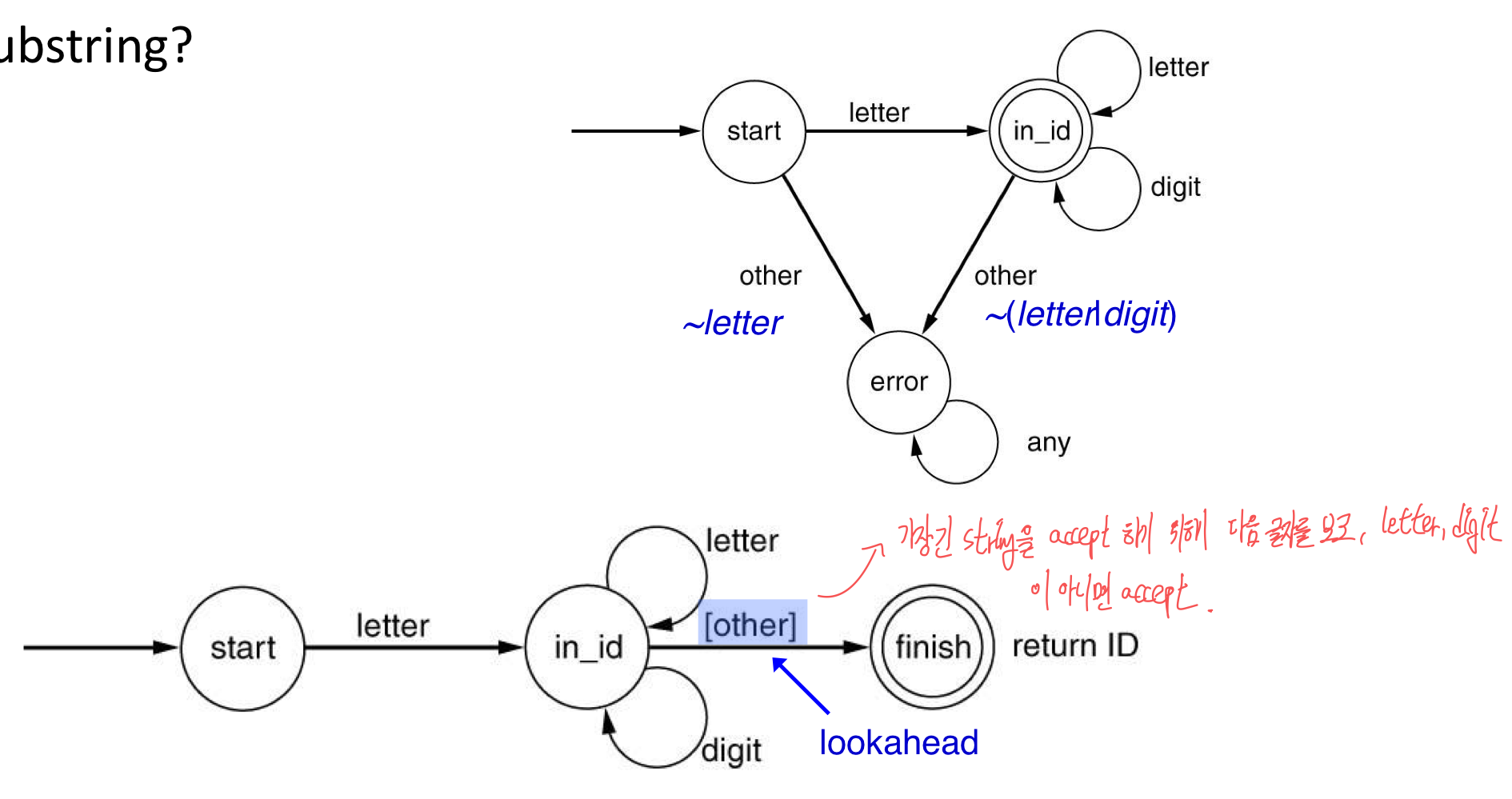
• lookahead and backtrack
  • single-character lookahead (다음 character을 내다 본다.)
    • xtemp = ytemp
  • backtrack (1개의 단어보다 더 멀리 본다.)
    • FORTRAN
      • DO99I = 1,10 (loop)
      • DO99I = 1.10 (assignment)

4) Class Problem

• A. What the diffrerence?
  • [abc] abc
• Extend the description of real on the previous slide to include numbers in scientific notation
  • -2.3E+17, -2.3e-17, -2.3E17

(+|-)?[0-9]+(.[0-9]+)?(Ee?[0-9]+)?

4) How to Break up Text

• REs를 혼자 사용하는 것은 충분하지 않고, 여러개가 matching 되었을 때, 선택할 rule이 필요하다.
  • Longest matching token wins
  • length가 같다면 prioirity로 결정한다.
    • Token의 정의 순서가 priority를 결정한다.
  • RE’s + prioritys + longest matching token rule = definition of lexer

5) Automatic Generation of Lexers

• 1970년대 중반, UNIX를 위해 Bell Labs에서 두 프로그램이 개발되었다.
  • Lex: transducer로서, 입력스트림을 yacc에서 처리되는 문법의 알파벳으로 변환한다.
    • Flex: lex의 빠른 버전으로, Free software foundation에 의해 나중에 개발되었다.
  • Yacc/bison - yet another compiler/compiler
• lexer generator의 Input
  • 우선 순위 순서에 따른 정규표현식 목록
  • 각 정규표현식과 관련된 작업
• Output
  • 입력 스트립을 읽고 정규 표현식에 따라 토큰으로 나누는 프로그램

a) Lex/Flex

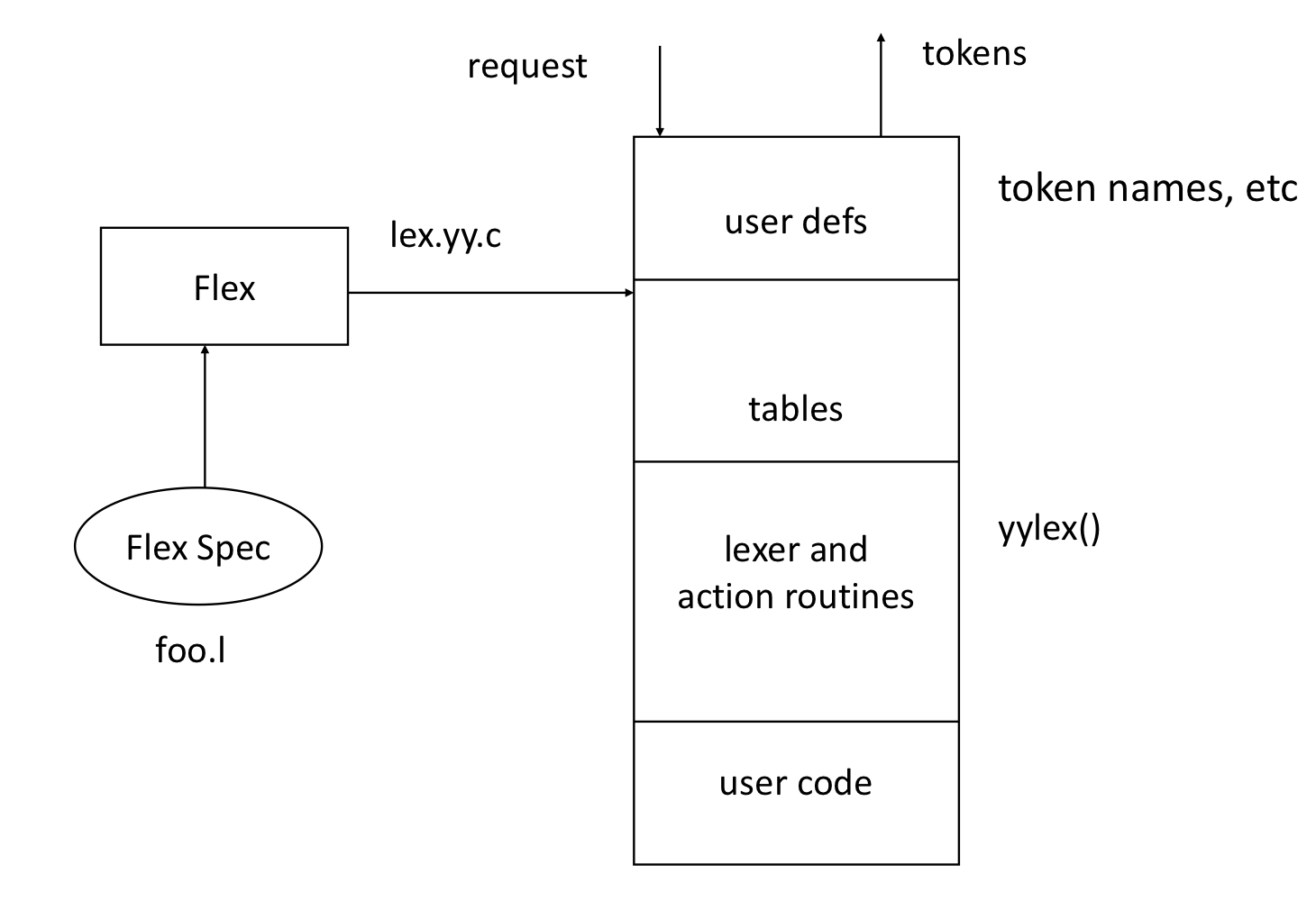
b) Lex Specification

• Definition section
  • “%{”와 “%}”사이에 포함된 모든 코드는 프로그램으로 복사된다. 일반적으로 parser에 의해 정의된 token이 포함된다.
  • User는 규칙에서 제공되는 복잡한 패턴에 이름을 제공 할 수 있다.
  • “%s” 지시문으로 시작되는 상태를 이 섹션에서 추가 정의 할 수있다.
  • Pattern and state definition은 반드시 column 1에 시작하여야 한다. (첫 열에 공백이 있는 모든 라인은 결과적으로 생성되는 C파일로 복사된다.)
• Rules section
  • lexical pattern과 pattern이 일치 할 때, 수행되어야 할 semantic action이 포함되어 있다.
  • Action은 반드시 {}로 둘러싸여야한다. (반드시 필요한 것은 아니다)
  • 다시, 첫 열에 공백이 있는 모든 라인은 결과로 생성되는 C program으로 복사된다.
• User function section
  • 이 섹션에 있는 모든 Line들은 최종 .c 파일로 복사된다.
  • 함수가 즉각적인 support routine이 아닌 경우에, 이러한 함수를 별도에 함수에 두는 것이 좋다.

%201%20ddbfd951639e4aef9896712a1d5325e5/Untitled%207.png)

c) Partical Flex Program

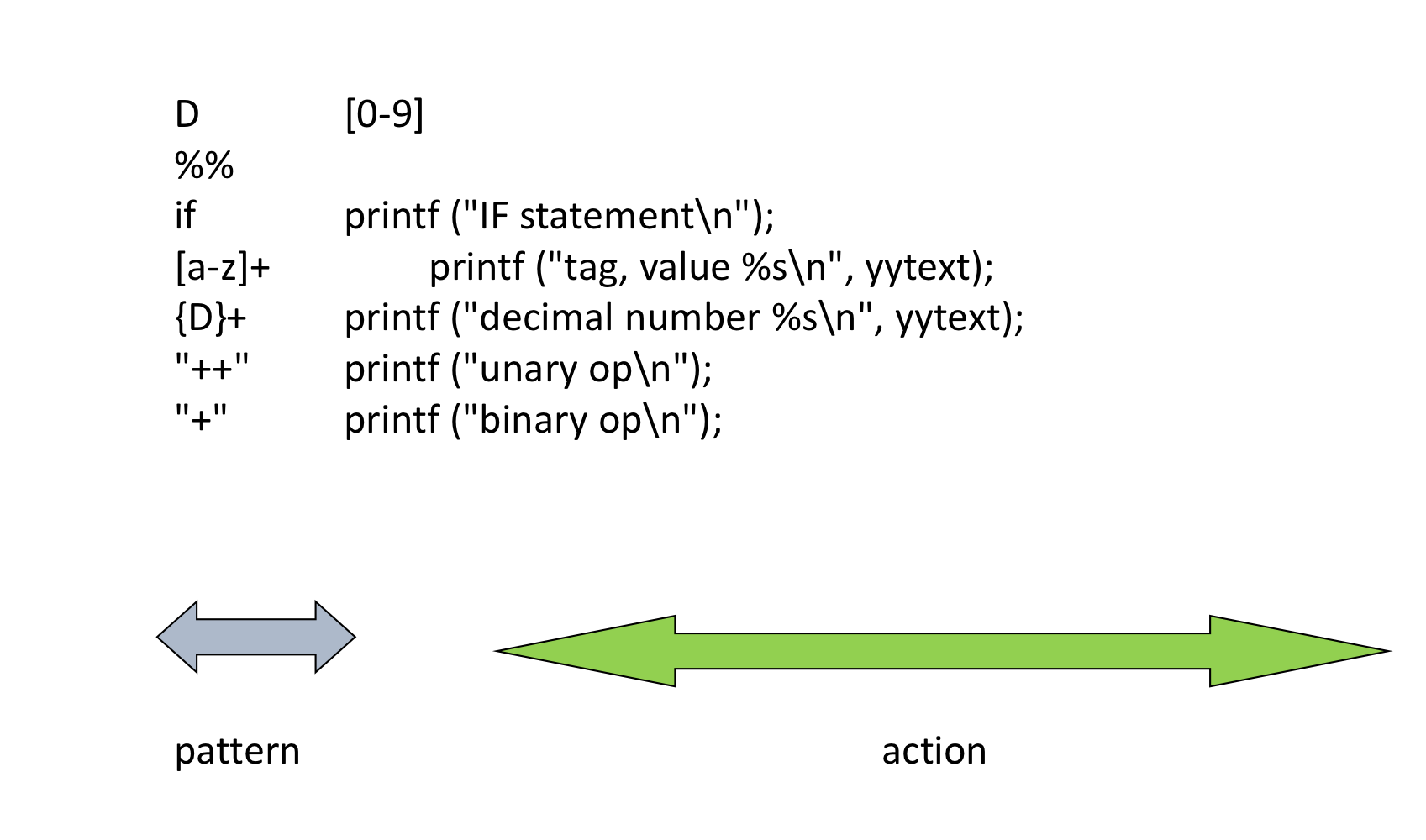
d) Lex Regular Expression Meta Chars

e) Lex program for the token

f) How Does Lex Work?

• lexical analysis의 일반적인 기초는 finite state automaton (FSA) 이다.
  • RE는 regular set들을 생성한다.
  • FSA는 regular set들을 인식한다.
• FSA - informal defn:
  • A finite set of states
  • state들 사이의 transition
  • An initial state(start)
  • final state의 집합 (accepting states)

2. FSA

• Non-deterministic finite automata (NFA)
  • 여러개의 transition들이 있을 수 있다. (input이 필요 없을 수도 있다.)
• Deterministic finite automata (DFA)
  • 현재 상태와 입력 문자에 따라 transition이 명확히 결정되는 것이다.
    • state에서 많아봤자 1개의 선택지가 존재한다.
  • 람다 transition이 없다.

1) NFA Example

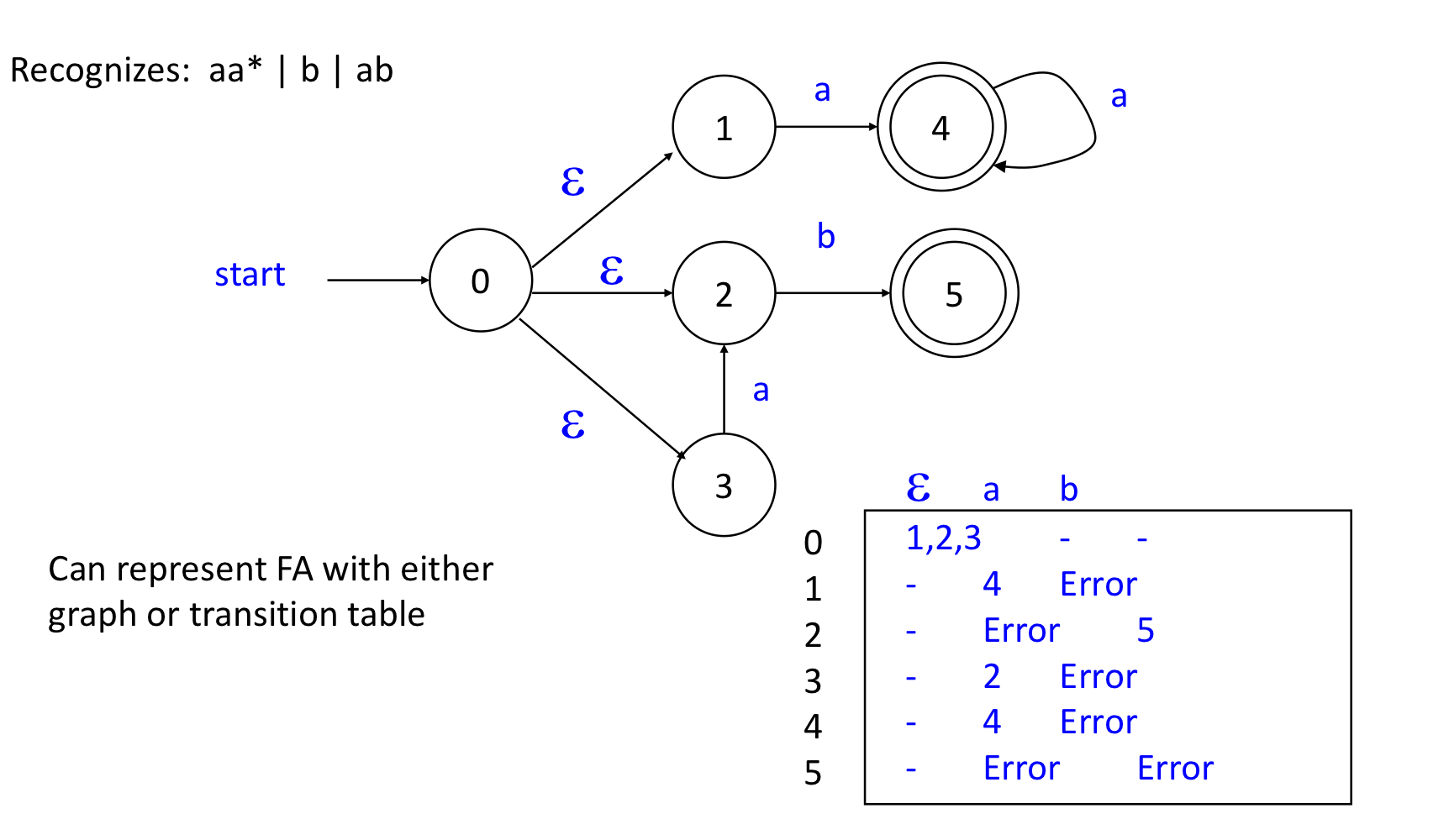
2) DFA Example

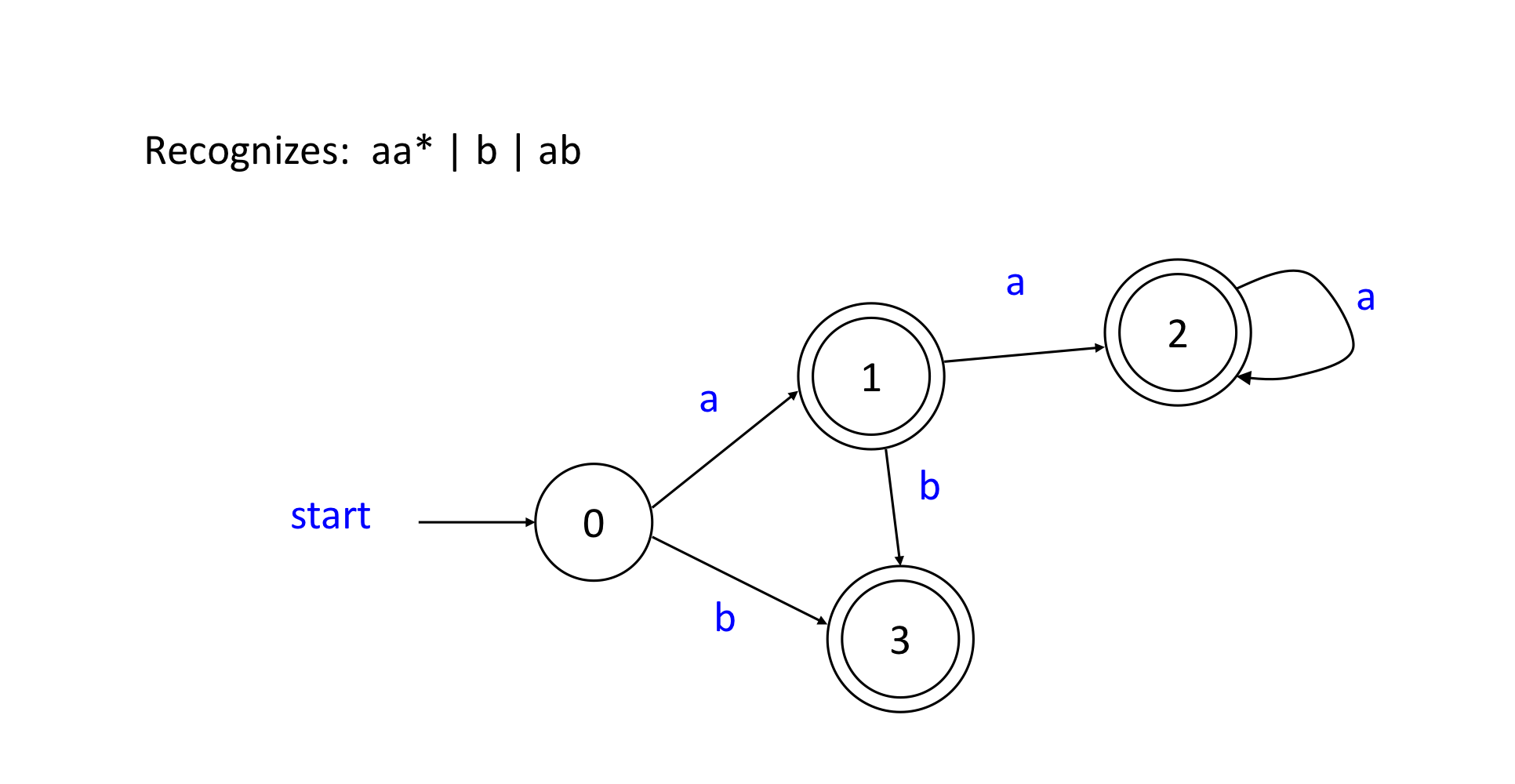
• 없는 transition들은 error state로 간다.

3) Finite automata

• Finite automata consists of
  • states
  • transitions (on symbols)
  • start state
  • accepting states
• Finite automata는 regular expression들로 표현 된 pattern을 인식하기 위해 사용된다.

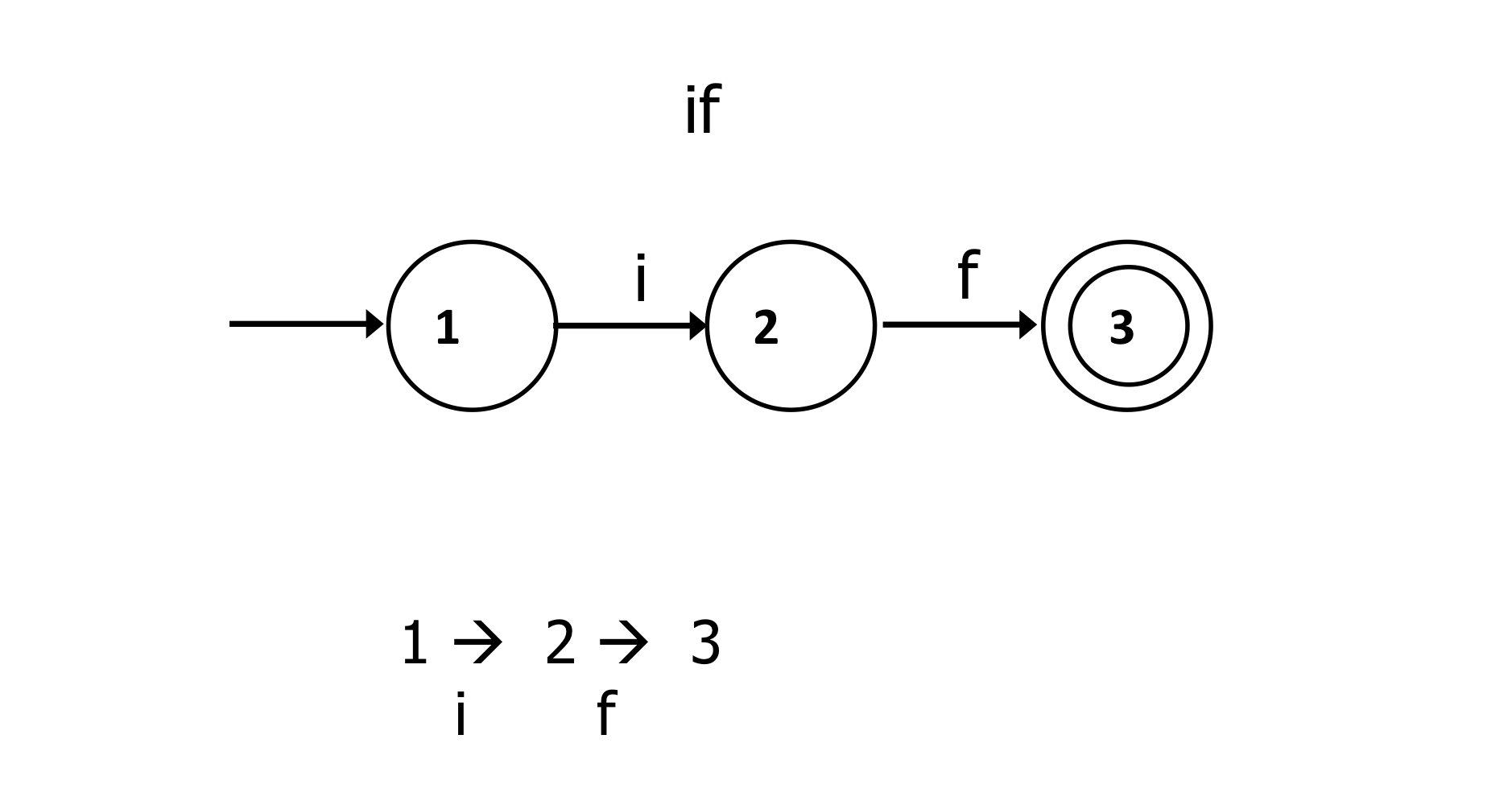
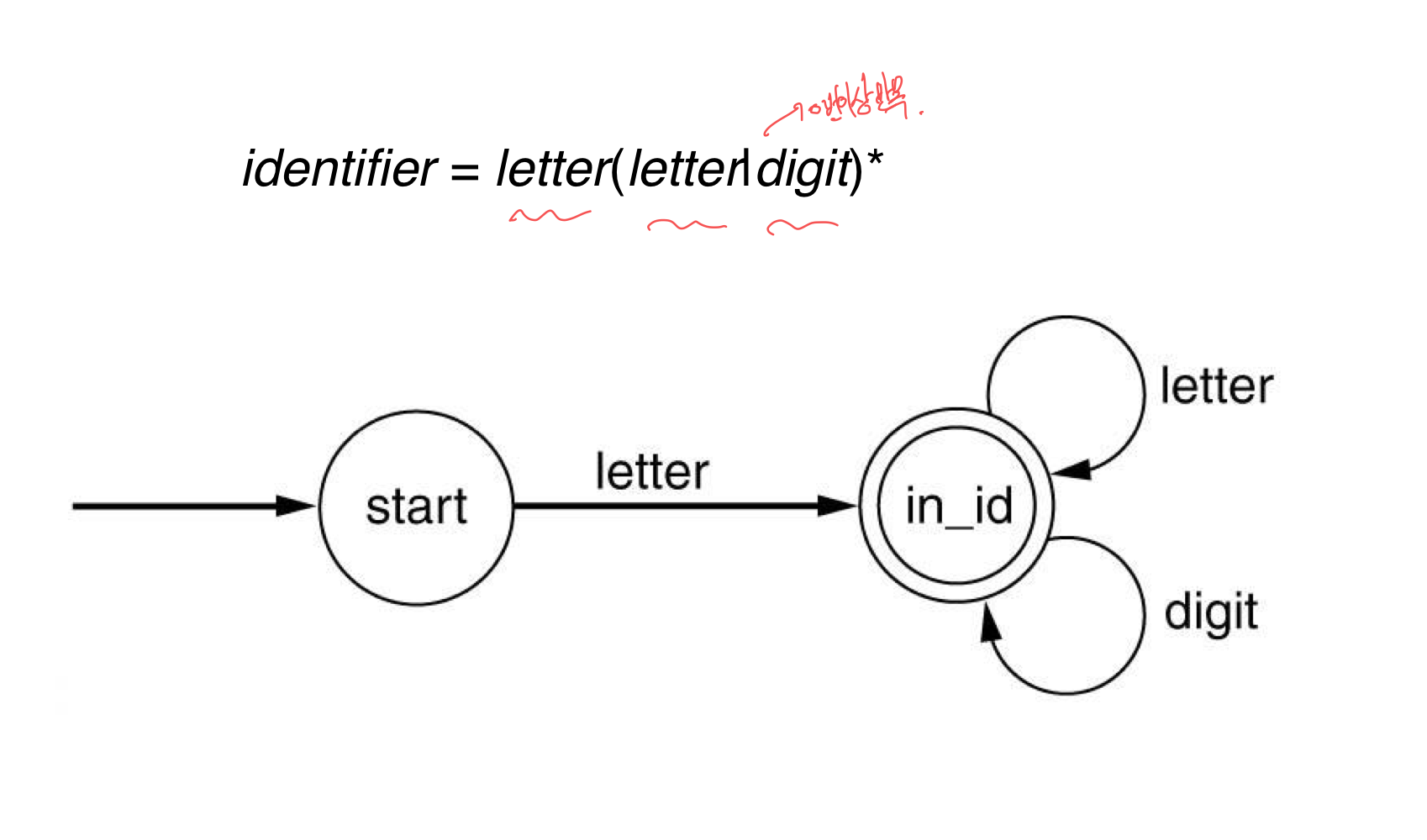
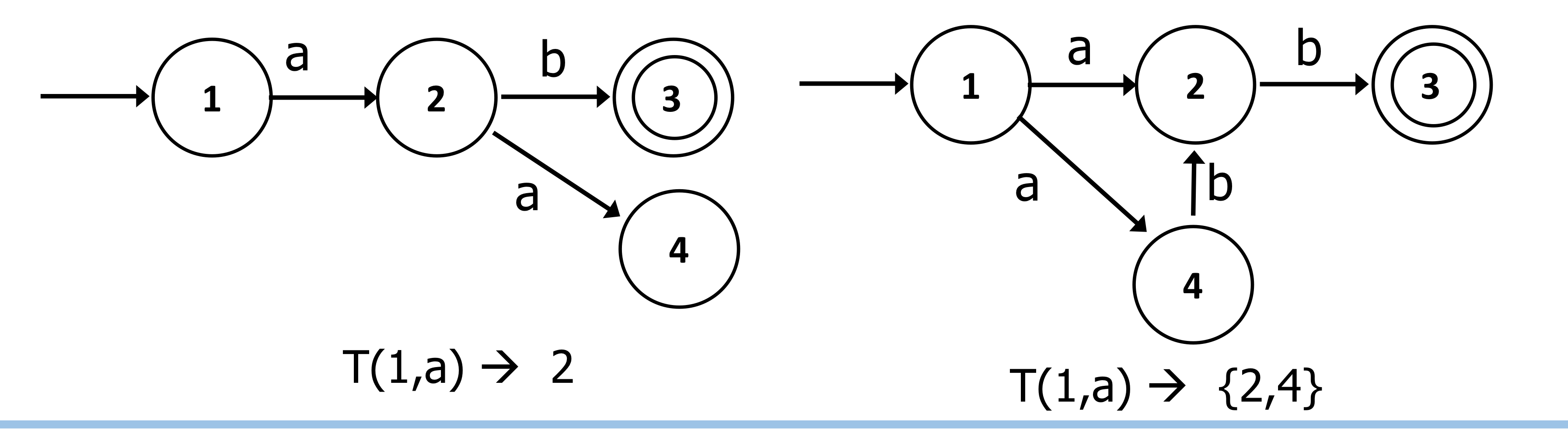
a) Mathematical definition of DFA

• A DFA M consists of an alphabet ∑, a set of states S, a transition function T: S x ∑→S, a start state s0 ∈ S, and a set of accepting states A ⊂ S. The language accepted by M, written L(M), is defined to be the set of strings of characters c1c2...cn with each ci ∈ ∑ such that there exist states s1 = T(s0, c1), s2 = T(s1, c2), ..., sn = T(sn-1, cn) with sn an element of A.

b) Finite automata

• Error transition들은 그려지지 않는다.

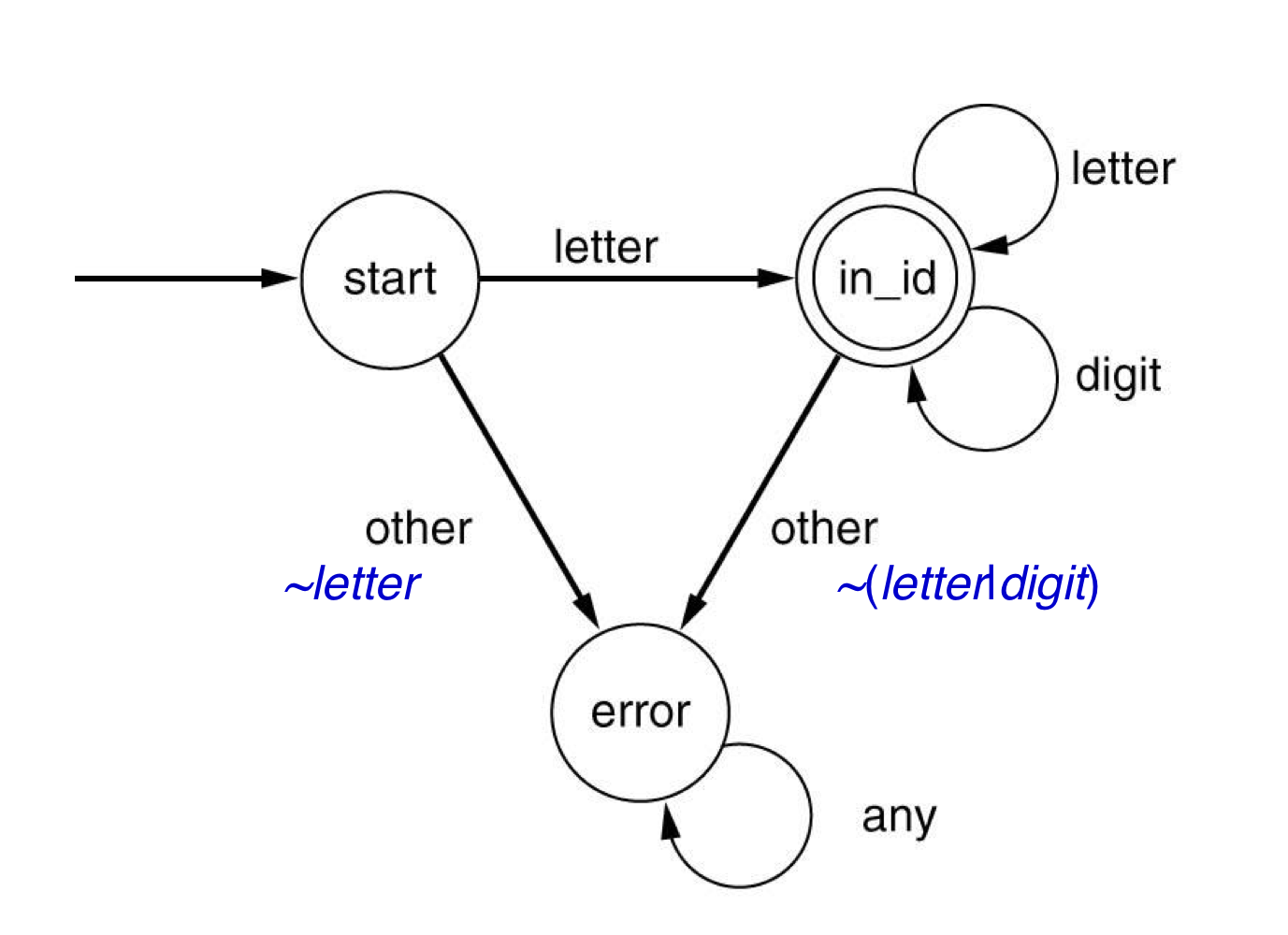
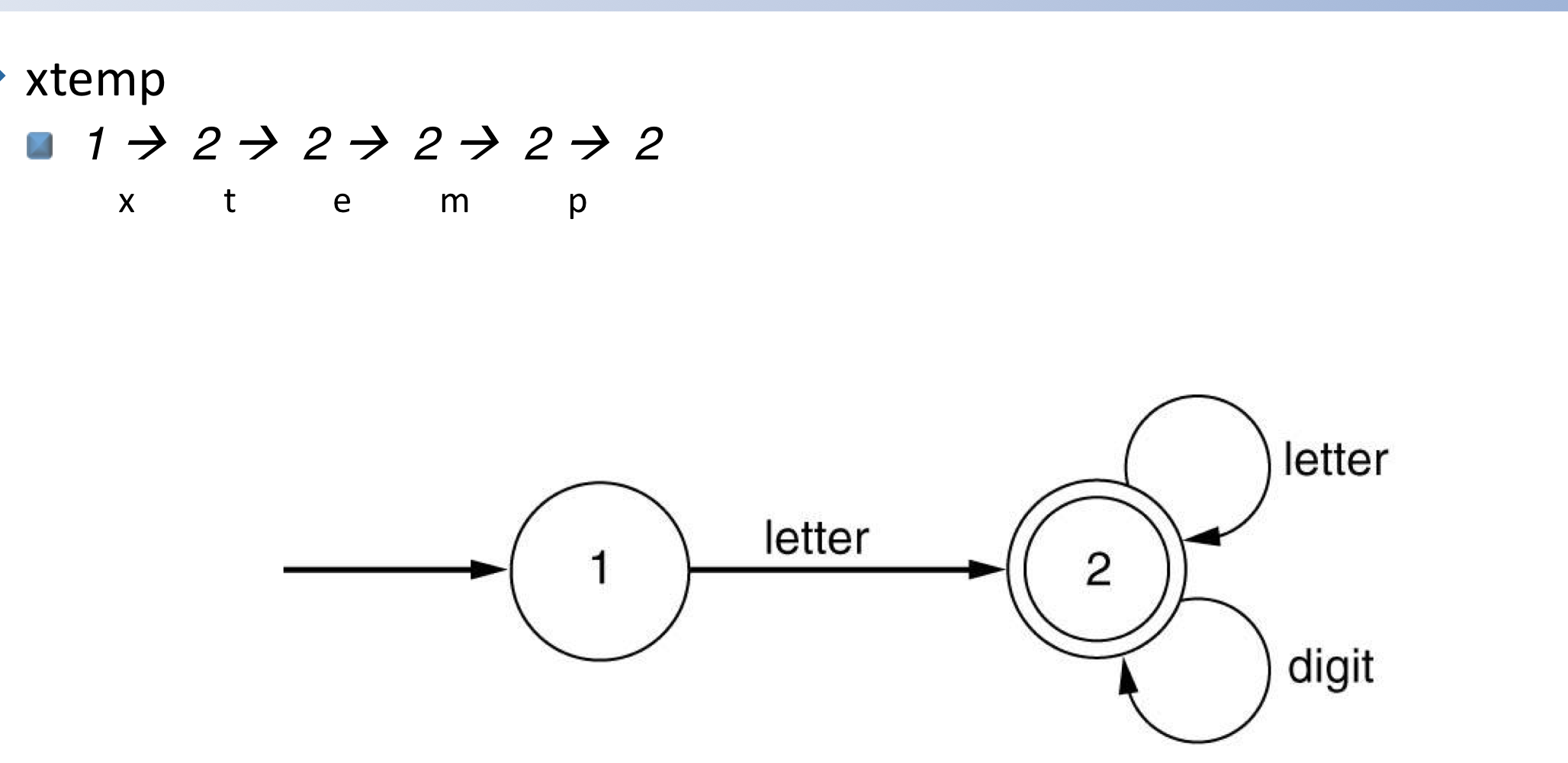
• DFA
  • state와 symbol이 주어지면, 다음 state는 unique하다.
• NFA
  • state와 symbole이 주어지면, 다음 state는 unique하지 않다.

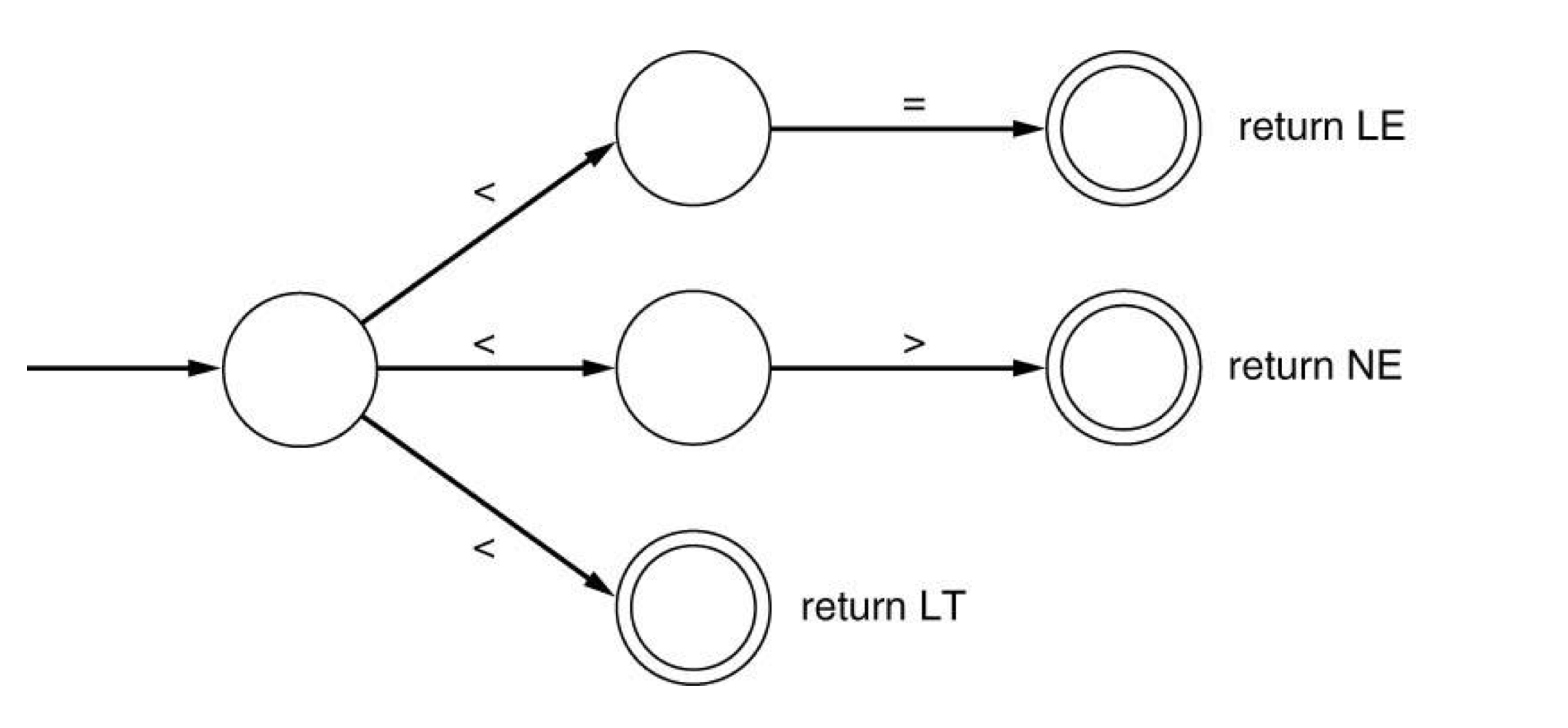
c) DFA

• Examples
  • The set of all strings over {a,b,c} containing exactly one b.
    • (a|c)b(a|c)

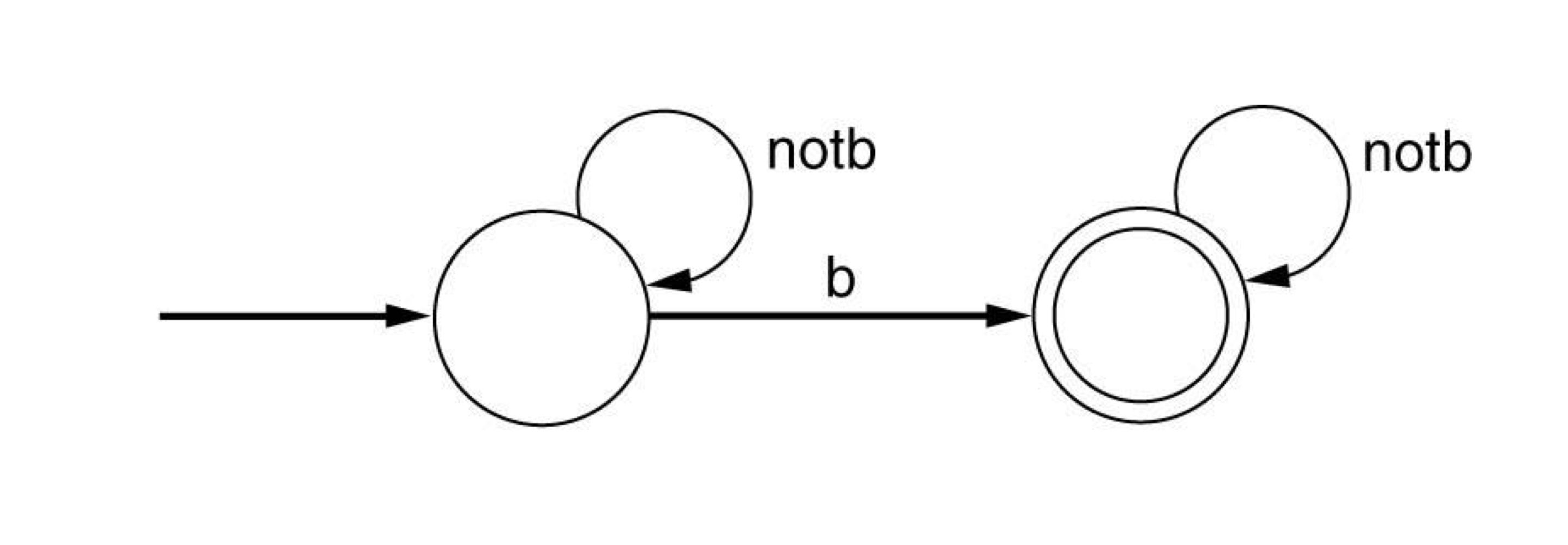
• Examples
  • The set of all strings over {a,b,c} containing at most one b.
    • (a|c)|(a|c)b(a|c)*
    • (a|c)(b|람다)(a|c)

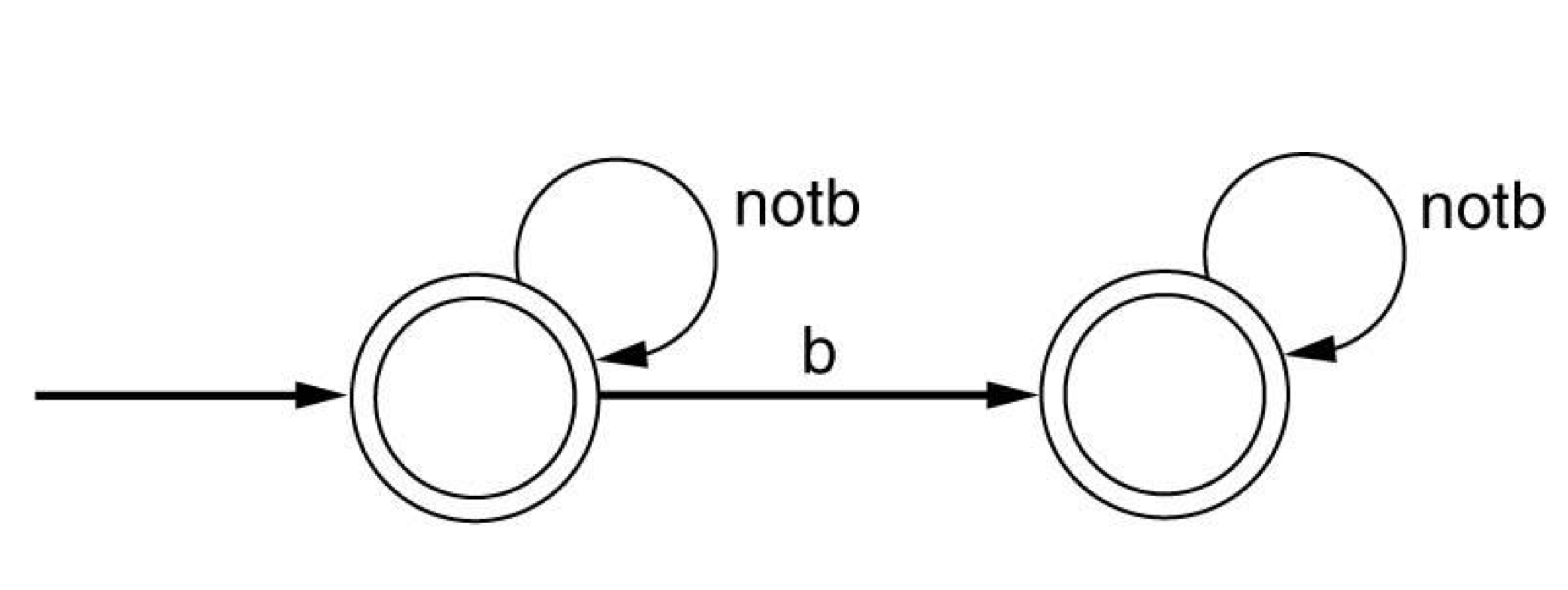
d) DFAs for PL tokens

• Examples

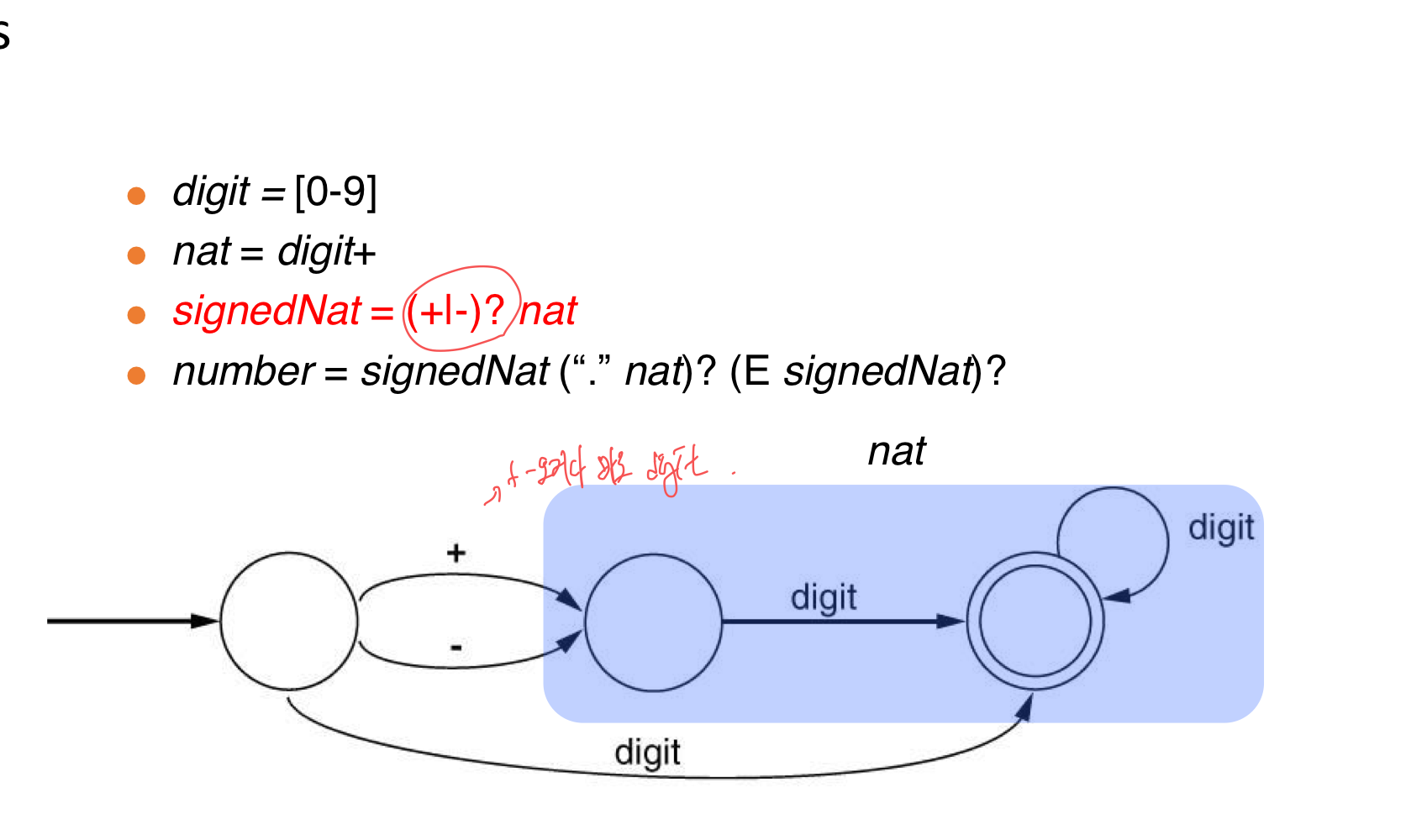
  • nat = [0-9]+
  • signedNat = (+|-)?nat
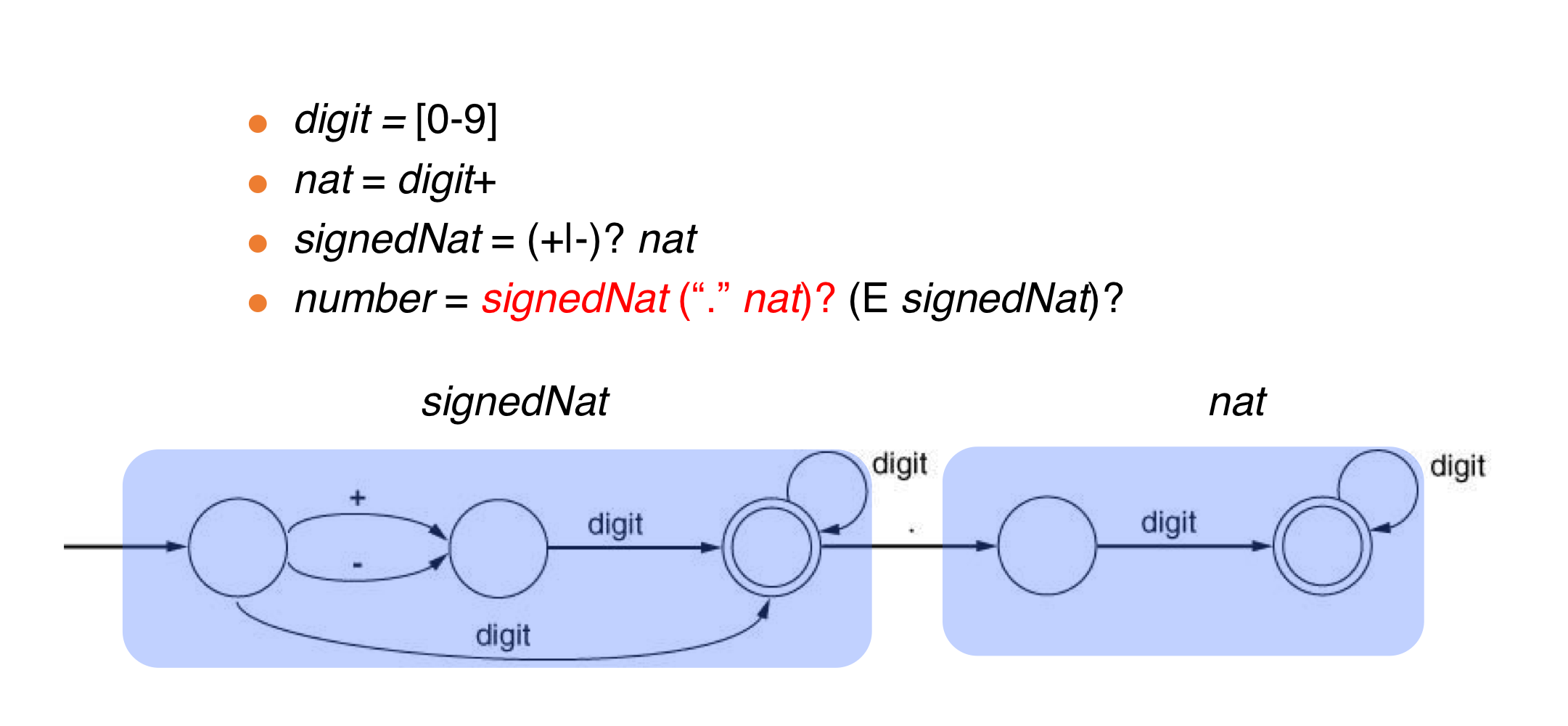
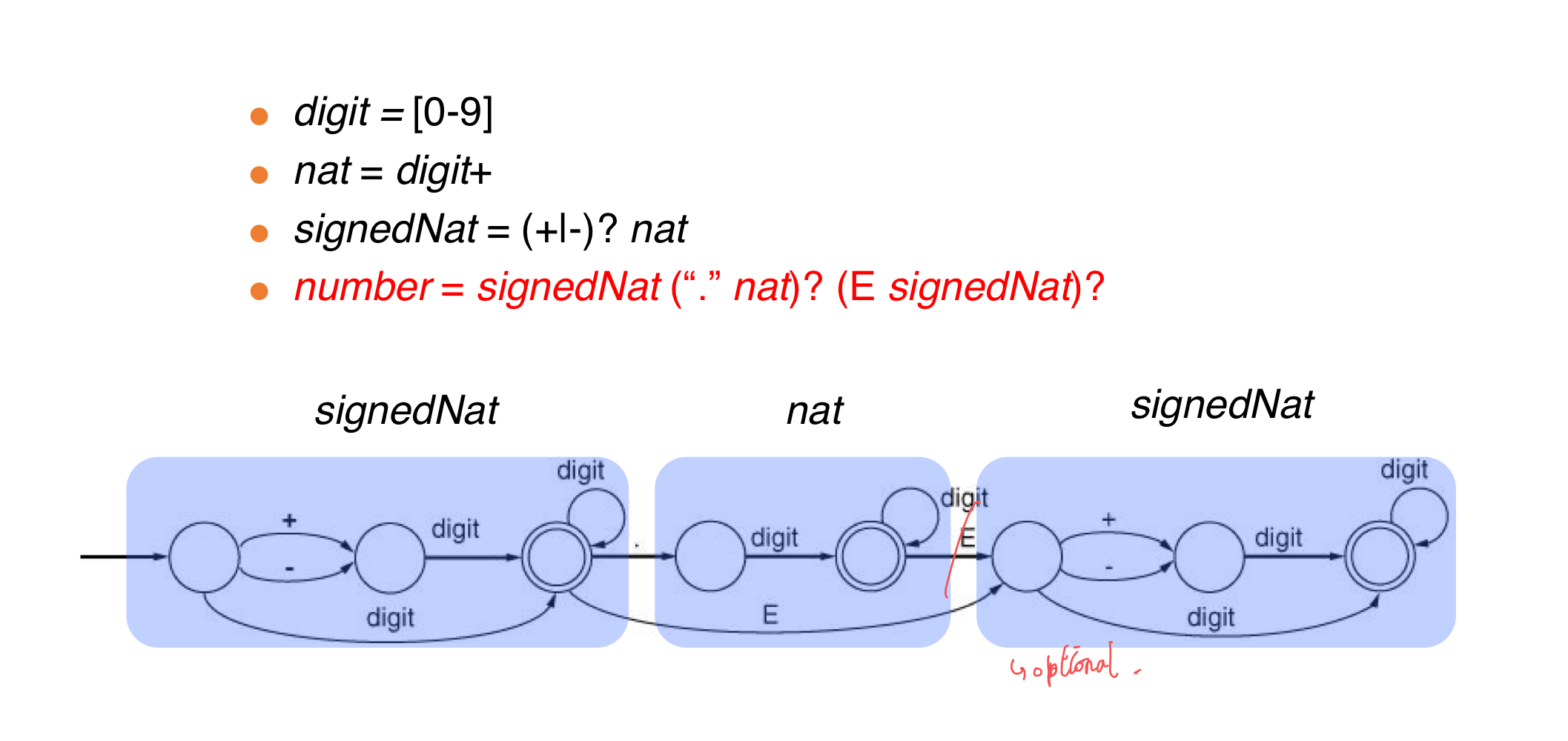
  • number = signedNat(”.”nat)?(E signedNat)?

• digit = [0-9]

• nat = digit+

• signedNat = (+|-)?nat

• number = signedNat(”.”nat)?(E signedNat)?

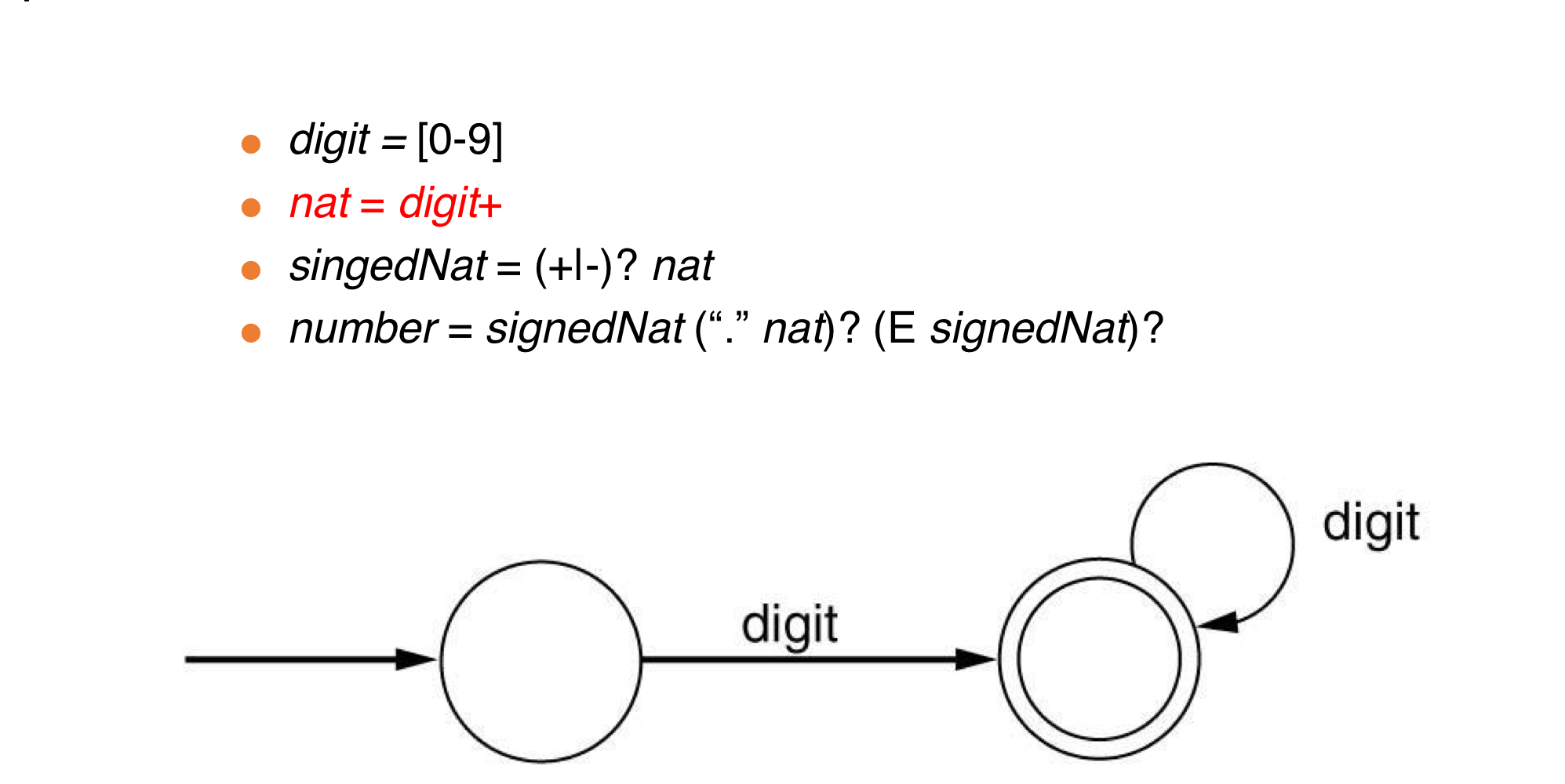
c) Merging DFAs

• a DFA for each token → DFA for some tokens

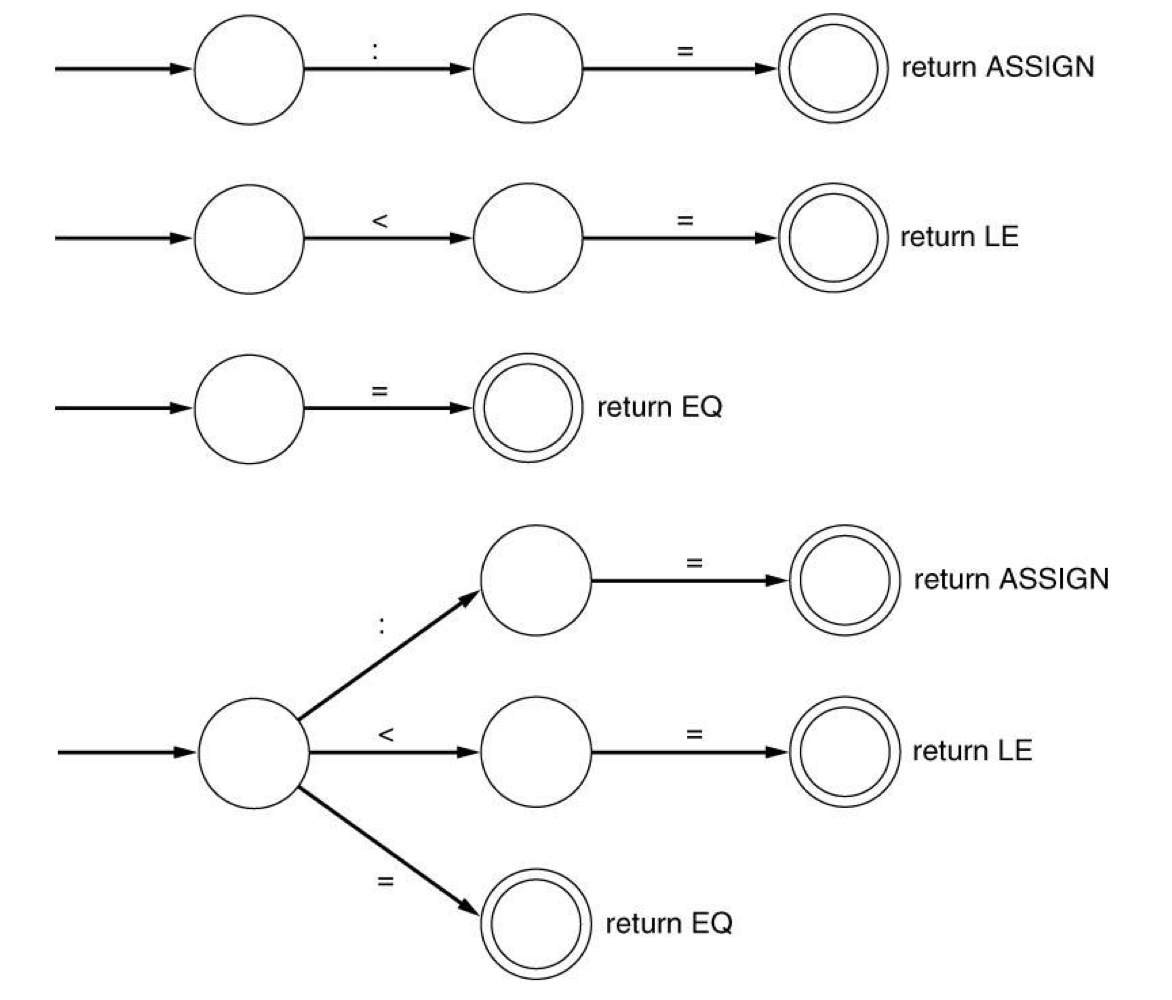
• same symbol로 시작한다면, DFA들을 merge한다.

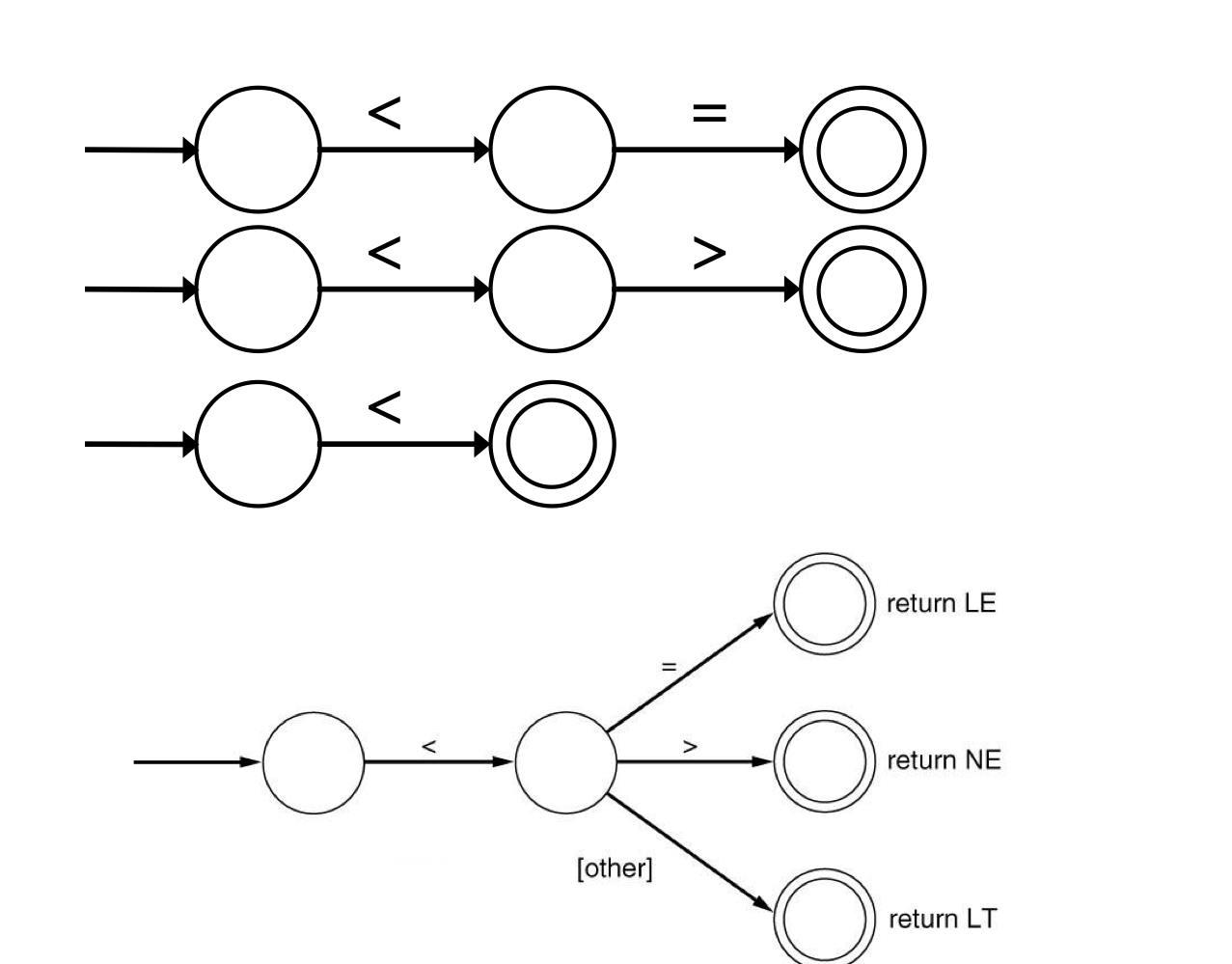
d) NFA

• state와 symbol이 주어진다면, 다음 state는 unique하지 않다.

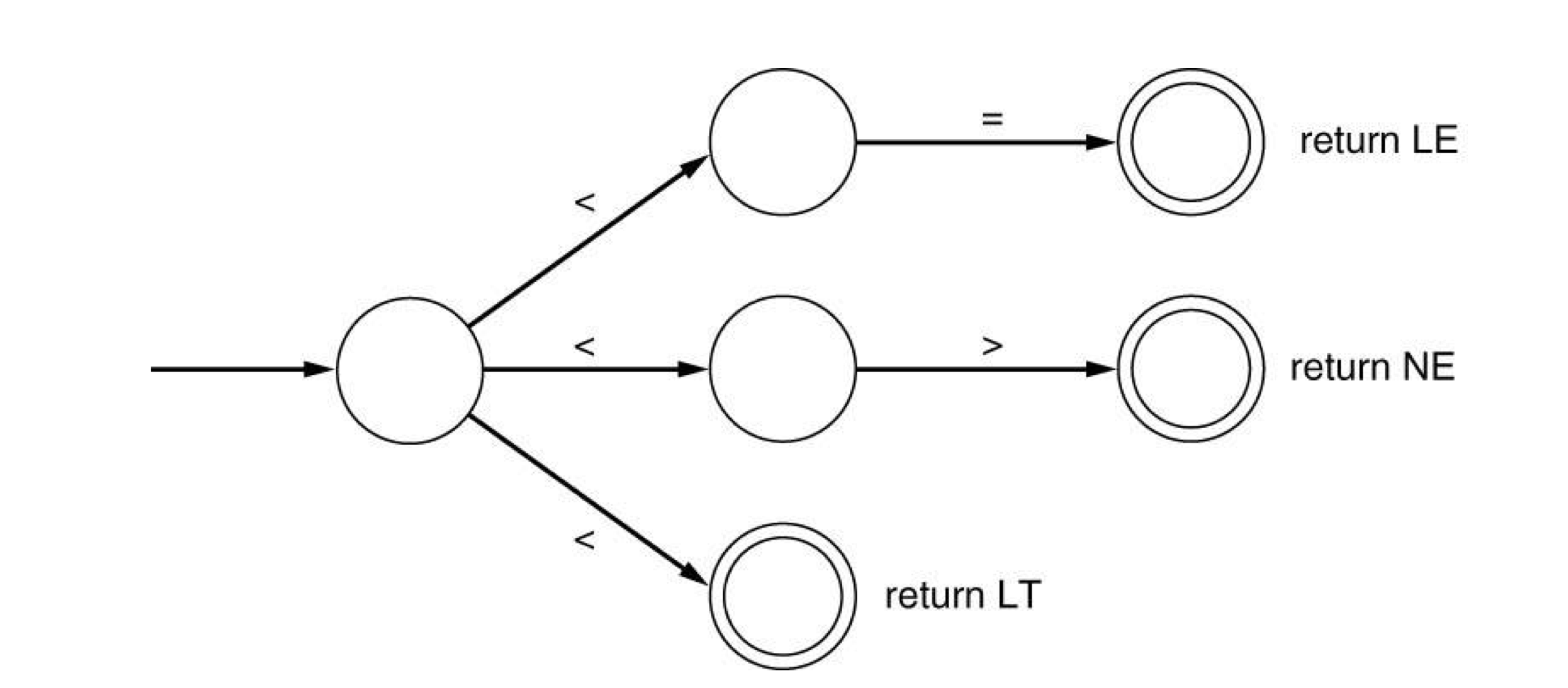
• 람다 transition도 포함할 수 있다.
• 람다 transition은 state를 combining하지 않고, automata를 merging할 수 있도록 만들어 준다.

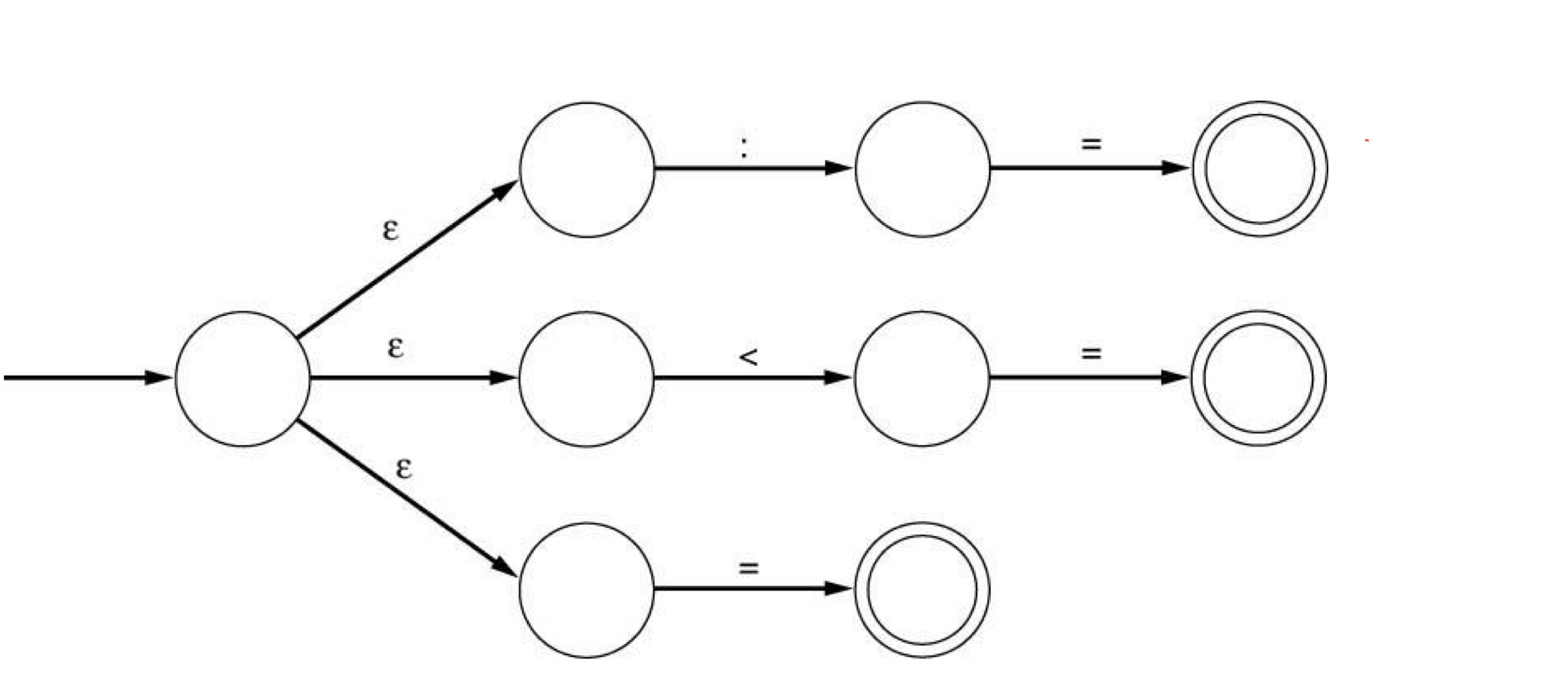
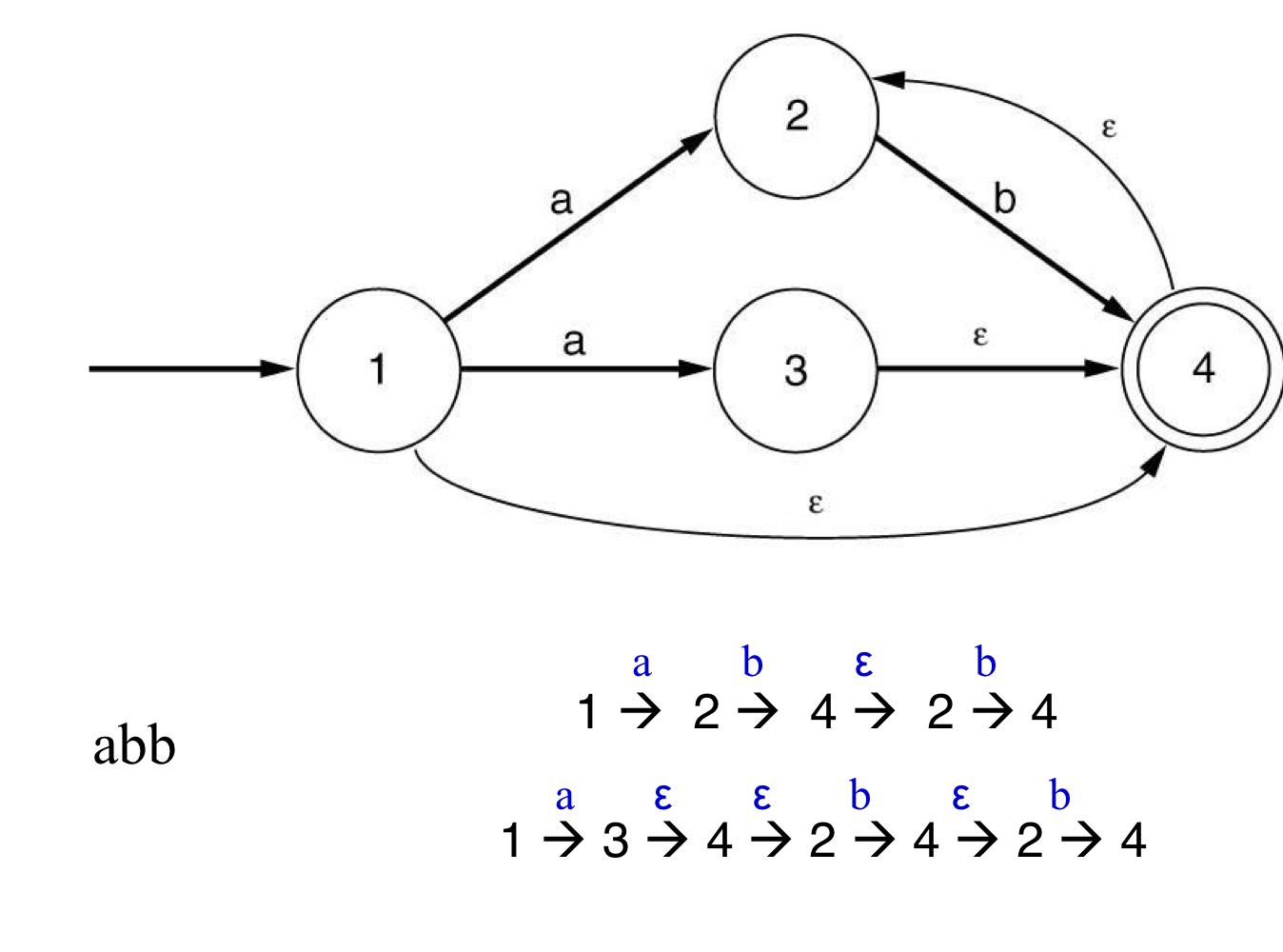
• ab+|ab|b or (a|람다)b*

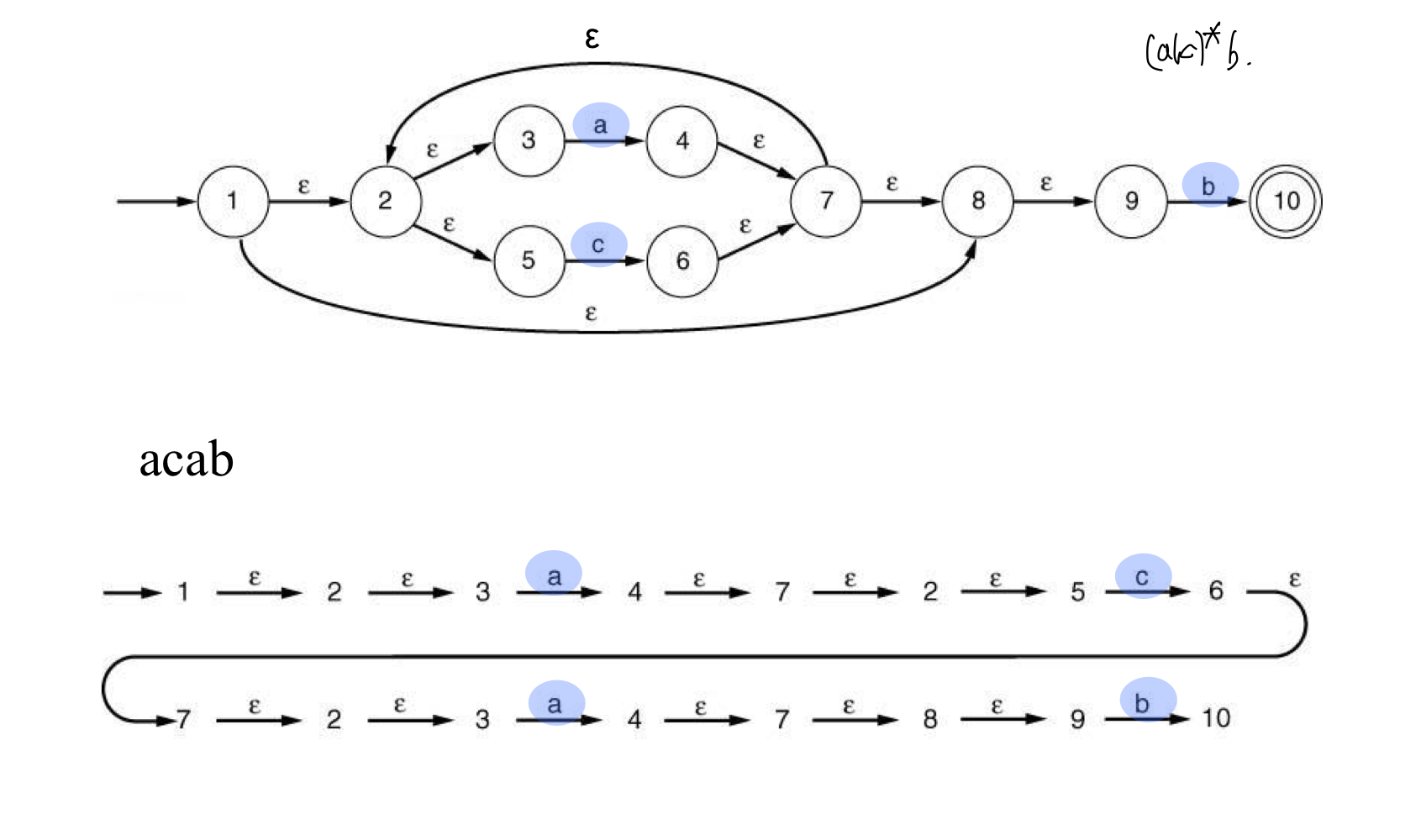
e) Finite Automata

• An alphabet Σ
  • the set of symbols: {a, b, …}
• A set of states S
  • normal states, a start state, a set of accepting states
• a transition function T (모든 state와 symbol의 pair)
  • T: SXΣ → S (DFA)
  • T: SX(Σ U {ε}) → p(S) (NFA)

• Finite automata에 의해 accept되는 strings
  • start state부터 시작해서 transition들을 사용해서 accepting state 중 하나로 도착 할 수 있는 strings.

f) NFA vs DFA

• DFA
  • 각 input에 대한 action이 완전히 결정되어 있다.
  • table-driven approach를 사용해서 구현된다.
  • 정규표현식을 구현하기 위해 더 많은 state들이 필ㅇ로하다.
• NFA
  • 각 step에서 선택 할 수 잇다.
  • 어떤 경로로든 accepting state에 도착하면, string을 accept한다.
  • 구현 방법이 명확하지 않다.