레드-블랙 트리(Red-Black Tree)
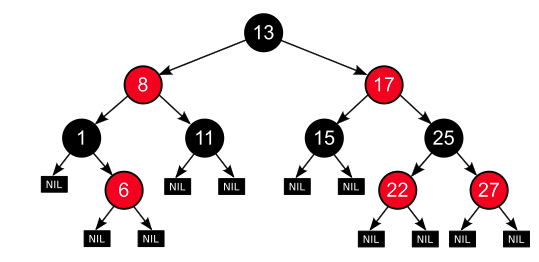
레드 블랙 트리는 자가 균형 이진 탐색 트리이다. 자가 균형 이진 탐색 트리라는것이 무엇일까?
기본적으로 레드 블랙 트리는 자가 균형 이진 탐색 트리라는 이름에서 알 수 있듯이, 이진 탐색 트리(BST)의 속성을 따르게 된다. 여기에 더해 자가 균형이라는 속성이 더해진 것이라고 이해하면 된다.
자가 균형 트리의 예로는 AVL 트리와 레드-블랙 트리가 있다. 이 포스팅에서는 레드-블랙 트리에 대해 정리해보려고 한다.
레드-블랙 트리의 장점
- 삽입, 삭제, 탐색 등의 연산이 모두 O(logN)의 시간복잡도를 가진다.
- 균형잡힌 트리의 형태를 유지하면서 연산이 가능하다.
- 대부분의 연산에서 최악의 경우에도 O(logN)의 시간복잡도를 보장한다.
이진 검색 트리(BST)도 평균적으로 O(logN)의 시간복잡도를 가지지 않나...?
일반적으로는 그렇다. 그러나 랜덤한 값이 아닌, 오름차순으로 정렬된 데이터 등이 들어올 경우에 이진 검색 트리는 한 방향으로 편향된 편향 트리가 된다. 아래 이미지와 같은 모습이 된다.
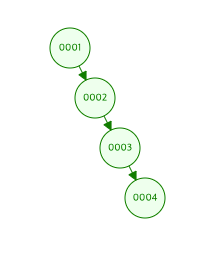
트리의 모습이 위와 같이 구성될 경우, 시간복잡도는 O(N)까지 늘어나게 된다. 레드-블랙 트리는 단순 이진 탐색 트리의 이러한 단점을 보완하기 위해 등장하였다.
레드-블랙 트리에 1, 2, 3, 4 순으로 정렬된 데이터로 삽입한 모습은 아래와 같다.
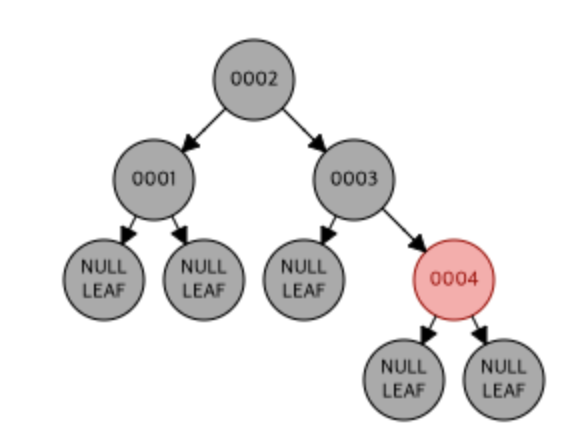
한 방향으로 편향되었던 이진 탐색 트리와는 다르게 좌우로 노드의 균형이 맞추어진 모습을 볼 수 있다. 그리고 한 가지 더 차이점을 발견할 수 있는데, 노드의 색이 검정색과 빨간색 으로 서로 다르게 칠해져있다는 것이다.
이제 레드-블랙 트리를 만들기 위해서 지켜져야하는 5가지 조건에 대해서 알아보자.
레드-블랙 트리의 조건
- 모든 노드는 빨간색 혹은 검정색이다.
- 루트 노드는 검정색 이다.
- 모든 리프 노드(NIL)들은 검정색이다. (*NIL : 위 그림에서 NULL LEAF에 해당한다.)
- 빨간색 노드의 자식은 검정색이다. (빨간색 노드가 연속으로 배치 될 수는 없다.)
- 모든 리프 노드에서 루트까지의 경로에서 만나는 검정색 노드의 갯수는 같다.
그렇다면 같은 자가 균형 트리인 AVL 트리와는 어떻게 다를까?
레드-블랙 트리 vs AVL 트리
| 특징 | 레드-블랙 트리 | AVL 트리 |
|---|---|---|
| 이진 탐색 트리 | O | O |
| 삽입/삭제/검색 시간 복잡도 | 최악 경우에도 O(logN) | 최악 경우에도 O(logN) |
| 삽입/삭제 성능 | AVL 트리에 비해 빠르다 | 레드-블랙 트리에 비해 느리다 |
| 검색 성능 | AVL 트리에 비해 느리다 | 레드-블랙 트리에 비해 빠르다 |
| 응용 사례 | linux kernel, Java TreeMap, c++ std::map 등등.. | dictionary, 한번 만들어 놓으면 삽입/삭제가 거의 없고 검색이 대부분인 상황에 사용된다. |
어떤 차이 때문에 삽입/삭제와 검색에 있어서 성능 차이가 나는지 묻는다면, 그 답은 균형을 잡는 기준에 있다.
두 트리 구조 모두 균형을 유지하는 트리이지만, 그 엄격함의 기준이 상이하다.
레드-블랙 트리의 경우 '대략적인' 균형을 잡지만, AVL 트리의 경우 '매우 엄격한' 균형을 잡는다. 이 때문에 삽입과 삭제에 있어서는 레드-블랙 트리가 유리하며, 검색에 있어서는 데이터가 잘 정렬되어있는 AVL 트리가 유리하게 된다.
AVL 트리가 검색 성능에 있어서 이점을 가지기는 하지만, 레드-블랙 트리와 비교하였을때 그리 유의미한 성능 차이는 아니며, 대부분의 경우 검색만 갖추기보다는 삽입/삭제 기능도 함께 다루는 경우가 많기 때문에 레드-블랙 트리의 사용성이 더 뛰어나다고 생각된다.

