[C언어] 레드-블랙 트리 삽입 연산 구현

채상엽·2023년 4월 4일
SW사관학교 정글c언어자료구조
0

SW사관학교 정글

목록 보기
22/35
post-thumbnail

이번 포스팅에서는 레드-블랙 트리에서의 삽입 연산이 어떤 과정을 통해 이루어지는지 그림을 통해 각 케이스를 알아보며, c언어로 직접 구현하는 것까지 기록해보려 한다.

만약 레드-블랙 트리의 개념에 대해서 잘 모르는 상태라면 레드-블랙 트리 기본 개념 잡기 포스팅을 읽고 오는 것을 추천한다.

레드-블랙 트리 삽입 연산

레드-블랙 트리에서는 기본적으로 이진 탐색 트리(BST)와 동일한 삽입 과정을 따르게 된다. 그러나 지난 포스팅에서 보았던 것처럼 편향된 구조를 방지하기 위해, 레드-블랙 트리에서는 회전을 통해 트리의 균형을 맞추게 된다. 아래의 움짤을 통해 간단하게 회전을 확인할 수 있다.

본격적으로 삽입을 시작하기 앞서, 다시 한번 레드-블랙 트리의 조건을 리마인드 해보자. 조건들은 다음과 같다.

레드-블랙 트리의 조건

  1. 모든 노드는 빨간색 혹은 검정색이다.
  2. 루트 노드는 검정색 이다.
  3. 모든 리프 노드(NIL)들은 검정색이다. (*NIL : 위 그림에서는 생략되어 있다.)
  4. 빨간색 노드의 자식은 검정색이다. (빨간색 노드가 연속으로 배치 될 수는 없다.)
  5. 모든 리프 노드에서 루트까지의 경로에서 만나는 검정색 노드의 갯수는 같다.

레드-블랙 트리에서 삽입할 때, 새롭게 추가된 노드들은 위 짤에서 볼 수 있듯이 항상 빨간색으로 삽입된다. 그런데 새롭게 삽입되는 노드들이 계속 빨간색이기 때문에, 어느 순간에는 Red-Red가 연속으로 배치되어 4번 규칙을 어기게 된다. 레드 블랙 트리는 이 경우에 Restructing과 Recoloring 을 이용해 레드-블랙 트리의 조건을 지키기 위해 균형을 맞추게된다.

1, 2, 3이 차례로 삽입 되었을때 과정을 차례로 그려보면 아래와 같다.

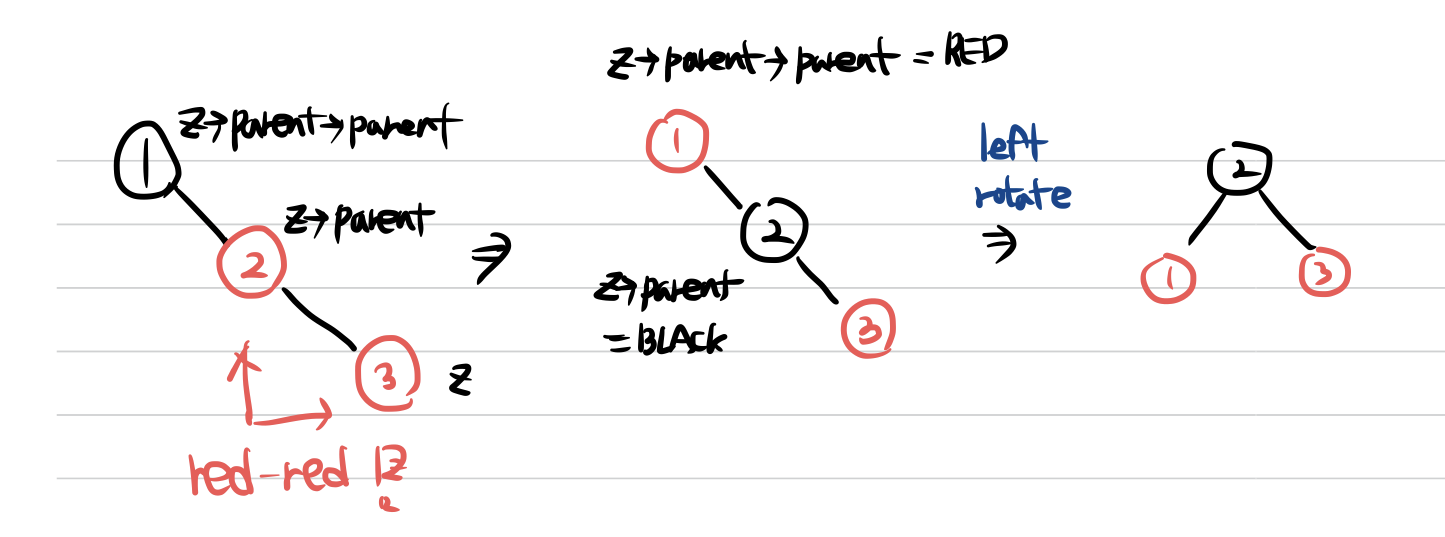
기본적으로 이진 탐색 트리의 삽입 과정을 그대로 따르기 때문에, 일단 먼저 이진 탐색 트리에서 삽입 하듯이 3까지 삽입하게 된다.

이렇게 막 삽입된 3의 값을 갖는 노드를 z라고 정의하겠다. 이때 자연스럽게 z의 부모 노드는 2가 되고, z의 조부모는 1이 되게 된다.

  • z->parent->parent = 1 (조부모)
  • z->parent = 2 (부모)
  • z = 3 (삽입 노드 자기 자신)

앞서 레드-블랙 트리의 균형을 맞추는 방법으로는 Restructing과 Recoloring이 있다고 했었다. 둘을 사용하는 경우는 아래와 같이 구분된다.

  1. z의 부모의 형제(삼촌) 노드가 red인 경우 -> Recoloring
  2. z의 부모의 형제(삼촌) 노드가 black인 경우 -> Restructing

위 사진의 경우에는 2번에 해당한다. 그 이유는 z부모의 형제는 1번 노드의 왼쪽 노드에 해당하는데, 1번 노드의 왼쪽 노드는 그림상에서는 비워져 있는 상태이다. 이 노드를 레드-블랙 트리에서는 NIL노드 라고 하는데, 이 노드는 항상 검정색을 갖는다. 따라서 z의 부모의 형제(삼촌) 노드가 **black**인 경우 에 해당하는 것이다.

이 포스팅에서는 편의를 위해 NIL 노드의 그림을 생략하며, 노드의 자식이 비워져 있는 경우 NIL 노드라고 생각해도 무방하다.

Restructing 동작 과정

현재 z와 z->parent(부모) 가 red-red가 되어 조건 4번을 어기고 있는 상태이다. 이를 해결 하기 위해서는 다음과 같은 과정을 따른다. (위 예제 기준)

  1. z의 부모의 색을 검정색으로 바꾼다.
  2. z의 조부모의 색을 빨간색으로 바꾼다.
  3. z의 조부모를 기준으로 왼쪽 회전을 수행한다.

여기서 회전의 방향은 현재 부모가 조부모를 기준으로 왼쪽에 위치했는지, 또 z가 부모를 기준으로 왼쪽에 위치했는지에 따라 달라지게 된다.

Recoloring 동작 과정

Recoloring은 아래 움짤을 보면 쉽게 이해할 수 있다.

새롭게 삽입되는 노드는 2이며, 부모 노드인 1의 형제인 5의 색깔이 빨간색 이므로, Recoloring을 수행해야하는 경우에 해당함을 확인할 수 있다. Recoloring은 다음과 같은 과정을 따른다.

  1. z의 부모의 색을 검정색으로 바꾼다.
  2. z의 부모의 형제의 색을 검정색으로 바꾼다.
  3. z의 조부모의 색을 빨간색으로 바꾼다.
  4. z의 조부모의 색을 빨간색으로 바꾸었기 때문에, 조부모의 부모와 또 다시 red-red가 발생할 가능성이 있기 때문에, z의 새로운 위치를 z의 조부모의 위치로 변경해준다.
  5. z의 새로운 위치에서 red-red가 발생하는지 다시 확인한다.

이를 c언어로 구현한 함수는 아래와 같다.
전체 코드 : https://github.com/saint6839/jungle-week-05

레드-블랙 트리 초기화 함수

rbtree *new_rbtree(void)
{
  rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
  node_t *new_node = (node_t *)calloc(1, sizeof(node_t)); // 초기화로 사용할 노드
  new_node->color = RBTREE_BLACK;
  new_node->key = 0;
  new_node->parent = p->nil;
  new_node->left = p->nil;
  new_node->right = p->nil;

  p->nil = new_node; // sentinel node
  p->root = p->nil; 
  return p;
}

왼쪽, 오른쪽 회전 함수

// x가 부모이고 y가 오른쪽 노드일때 y를 부모로 바꾸고 x를 왼쪽 노드로 회전 시키는 함수
void left_rotate(rbtree *t, node_t *x)
{
  node_t *y = x->right; // x의 오른쪽 노드의 주소를 선언함
  x->right = y->left;   // y의 왼쪽 노드를 x의 오른쪽으로 옮김
  if (y->left != t->nil)
  {                      // 만약 y의 왼쪽 노드가 NIL이 아니라면,
    y->left->parent = x; // 기존 y의 왼쪽에 있던 노드의 parent 노드를 x로 맞추어준다.
  }
  y->parent = x->parent; // x의 자리에 y가 올라왔으므로, 기존 x의 부모를 y의 부모로 바꾸어준다.
  if (x->parent == t->nil)
  {              // 만약 x의 부모가 NIL 이라면, root 노드라는 의미이므로,
    t->root = y; // y를 트리의 root로 선언한다.
  }
  else if (x == x->parent->left)
  {                      // 만약 x가 회전 되기 전에 부모의 왼쪽에 위치한 노드였다면,
    x->parent->left = y; // x부모의 왼쪽을 y로 바꾸어준다.
  }
  else
  {                       // 아니라면, x가 회전 되기 전에 부모의 오른쪽에 위치했다는 의미이므로,
    x->parent->right = y; // x부모의 오른쪽을 y로 바꾸어준다.
  }
  y->left = x;   // y의 왼쪽을 x로 바꾸어준다.
  x->parent = y; // x의 부모를 y로 바꾸어준다.
}

// y가 부모이고 x가 왼쪽 노드일때 x를 부모로 바꾸고 y를 오른쪽 노드로 회전 시키는 함수
void right_rotate(rbtree *t, node_t *y)
{
  node_t *x = y->left; // y의 왼쪽 노드를 선언함
  y->left = x->right;  // x의 오른쪽 노드를 y의 왼쪽으로 옮겨줌
  if (x->right != t->nil)
  {                       // x의 오른쪽이 NIL이 아니라면,
    x->right->parent = y; // 기존 x의 오른쪽에 있었던 노드의 parent 노드를 y로 맞추어준다.
  }
  x->parent = y->parent; // y의 자리에 x가 올라왔으므로, 기존 y의 부모를 x의 부모로 바꾸어준다.
  if (y->parent == t->nil)
  {              // 만약 y의 부모가 NIL 이라면, root 노드라는 의미이므로,
    t->root = x; // x를 트리의 root로 선언한다.
  }
  else if (y == y->parent->left)
  {                      // 만약 y가 회전 되기 전에 부모의 왼쪽에 위치한 노드였다면,
    y->parent->left = x; // y부모의 왼쪽을 x로 바꾸어준다.
  }
  else
  {                       // 아니라면, y가 회전 되기 전에 부모의 오른쪽에 위치했다는 의미이므로,
    y->parent->right = x; // y부모의 오른쪽을 x로 바꾸어준다.
  }
  x->right = y;  // x의 오른쪽을 y로 바꾸어준다.
  y->parent = x; // y의 부모를 x로 바꾸어준다.
}

RED-RED 발생으로 인해, 트리의 균형 조정이 필요할 경우 트리 구조를 수정하는 함수

void rbtree_insert_fixup(rbtree *t, node_t *z)
{
  printf("%d", z->parent->color);
  while (z->parent->color == RBTREE_RED)
  { // 새로 삽입된 노드는 RED인데, 부모 또한 RED인 경우에 FIXUP 수행
    if (z->parent == z->parent->parent->left)
    {                                       // z의 부모가 z조부모의 왼쪽 서브트리일 경우
      node_t *y = z->parent->parent->right; // z의 삼촌(부모 형제) 노드
      if (y->color == RBTREE_RED)
      {                                        // z의 삼촌 노드가 RED일 경우
        z->parent->color = RBTREE_BLACK;       // z의 부모 색 BLACK로 변경
        z->parent->parent->color = RBTREE_RED; // z의 조부모 색 RED로 변경
        y->color = RBTREE_BLACK;               // z의 삼촌 색 BLACK으로 변경
        z = z->parent->parent;                 // z의 위치를 z의 조부모로 변경 (z의 조부모가 새롭게 RED가 된 상태이므로, z의 조부모의 부모와 RED-RED 상태가 됐을 가능성 고려)
      }
      else
      { // z의 삼촌 노드가 BLACK일 경우
        if (z == z->parent->right)
        { // z가 z부모의 오른쪽 서브 트리일 경우
          z = z->parent;
          left_rotate(t, z); // z의 부모를 기준으로 왼쪽 회전 시켜서, 트리의 균형을 맞춘다.
        }
        z->parent->color = RBTREE_BLACK;       // z의 부모색을 BLACK으로 변경
        z->parent->parent->color = RBTREE_RED; // z의 조부모의 색을 RED로 변경
        right_rotate(t, z->parent->parent);    // z의 조부모를 기준으로 오른쪽 회전 시켜서, 트리의 균형을 맞춘다.
      }
    }
    else 
    { // z의 부모가 z조부모의 오른쪽 서브트리일 경우 -> 위 주석 설명의 반대로 이해하면 된다.
      node_t *y = z->parent->parent->left;
      if (y->color == RBTREE_RED)
      { // z의 삼촌 노드가 RED일  경우
        z->parent->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        y->color = RBTREE_BLACK;
        z = z->parent->parent;
      }
      else
      { // z의 삼촌 노드가 BLACK일 경우
        if (z == z->parent->left)
        { // z의 위치가 z부모의 왼쪽일 경우
          z = z->parent;
          right_rotate(t, z);
        }
        z->parent->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        left_rotate(t, z->parent->parent);
      }
    }
  }
  t->root->color = RBTREE_BLACK;
}

새로운 노드 삽입 함수

node_t *rbtree_insert(rbtree *t, const key_t key)
{

  node_t *y = t->nil;
  node_t *x = t->root;

  node_t *z = (node_t *)calloc(1, sizeof(node_t));
  z->key = key;
  // 이진 탐색 트리(BST)의 삽입과 동일하다
  while (x != t->nil) {
    y = x; // y = x가 이동하며 탐색한 z가 삽입될 위치
    if (z->key < x->key)
      x = x->left;
    else
      x = x->right;
  }

  z->parent = y;

  if (y == t->nil {
    t->root = z;
  } else if (z->key < y->key) {
    y->left = z;
  } else {
    y->right = z;
  }

  z->left = t->nil;
  z->right = t->nil;
  z->color = RBTREE_RED;

  // red-red인 경우 찾아서 노드 위치 수정
  rbtree_insert_fixup(t, z);
  return t->root;
}

출처

profile
채상엽
프로게이머 연습생 출신 주니어 서버 개발자 채상엽입니다.
이전 포스트

[C언어] 레드-블랙 트리 기본 개념

다음 포스트

[알고리즘] 백준 2565 전깃줄

0개의 댓글