본격적으로 포스팅을 시작 하기 전, 만약 레드-블랙 트리의 개념이 익숙하지 않거나 삽입 연산이 어떻게 이루어지는지 모르는 상태라면 아래 포스팅을 통해 간단하게나마 개념을 학습하고 삭제를 학습하는 것을 추천한다.
레드-블랙 트리의 조건
- 모든 노드는 빨간색 혹은 검정색이다.
- 루트 노드는 검정색 이다.
- 모든 리프 노드(NIL)들은 검정색이다.
- 빨간색 노드의 자식은 검정색이다. (빨간색 노드가 연속으로 배치 될 수는 없다.)
- 모든 리프 노드에서 루트까지의 경로에서 만나는 검정색 노드의 갯수는 같다
삭제에서도 마찬가지로 기본적으로는 이진 탐색 트리(BST)의 삭제 과정을 따르며, 삭제 이후에 위의 5가지 조건을 만족시키기 위한 동작을 수행하게 된다.
일단 삭제
먼저 이진 탐색 트리에서의 삭제와 동일한 방법으로 노드를 삭제한다. 이 경우는 두 가지로 나누어 볼 수 있다.
- 삭제하려는 노드가 자식 노드를 한 개 가지고 있거나 없을 경우
- 삭제하려는 노드가 곧 삭제될 노드이다.
- 삭제하려는 노드가 자식 노드를 두 개 모두 가지고 있을 경우
- 삭제 대상의 오른쪽 서브트리에서의 최솟값(successor)을 찾아 삭제한다.
- 아래 그림의 경우 2를 지우려고 한다면, 2는 자식 노드가 두 개 있고, 오른쪽 서브 트리의 최솟값인 3이 2의 successor 노드가 된다. 그러므로 이 경우 삭제 되는 노드는 3이 된다.
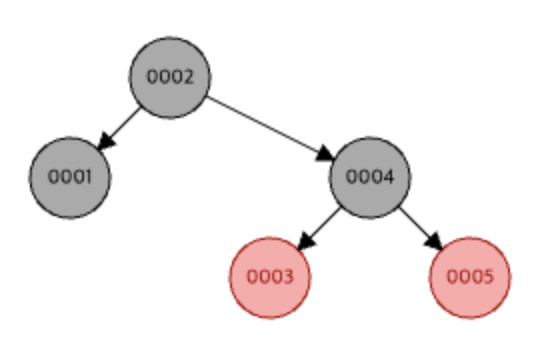
그리고..?
1번 케이스인 경우
만약 1번 케이스이면서, 삭제 대상이 빨간색 노드인 경우에는 지우더라도 5번 조건에 위배되지 않기 때문에 별도의 후처리 없이 바로 삭제한다.
그러나 1번 케이스이면서, 삭제 대상이 검정색 노드인 경우에는 해당 노드를 삭제할 경우 5번 조건이 깨지기 때문에 5번 조건을 다시 맞추어주기 위해 트리 노드의 위치를 조정하는 작업을 수행하게 된다.
2번 케이스인 경우
만약 2번 케이스이고, 지워질 노드는 z. successor 노드는 y라고 하였을때 y는 z의 색깔만 물려 받은채로 z의 위치로 올라가게 된다.
균형 맞추기
검정색 노드가 지워질 경우에는 해당 경로의 검정 노드의 수가 한 개 줄어들어, 5번 조건을 지키지 못하기 때문에 새롭게 균형을 맞추어 주어야한다. 이때 발생할 수 있는 경우의 수는 크게 다음 4가지로 나누어볼 수 있다.
그 전에 먼저 알아두어야하는 조건이 있다. extra black 이라는 개념이다. extra black이란 삭제된 z노드의 위치에 추가적인 검정색 노드 하나를 추가적으로 부여하는 개념이다. 아래 그림에서 만약 노드 1을 삭제한다면 extra node는 다음과 같이 위치하게 된다
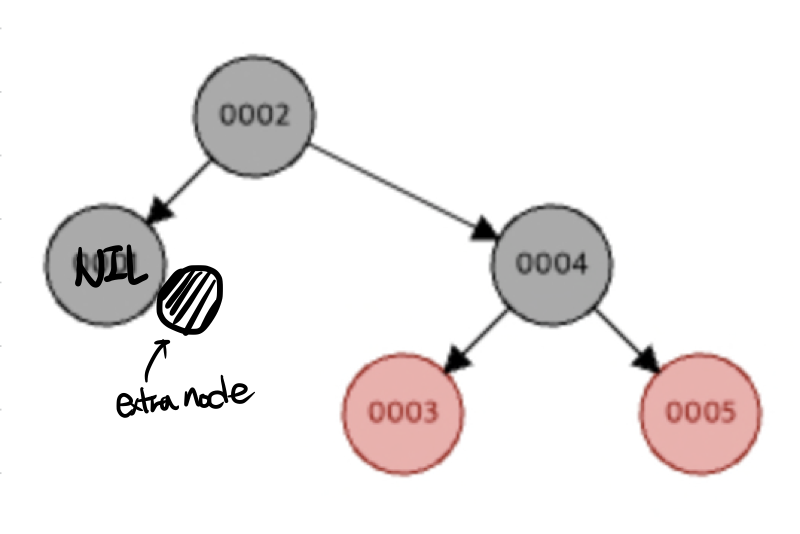
기존 노드1은 NIL 노드가 된다. NIL 노드는 기본적으로 검정색을 갖는데, 여기에 추가적인 extra black이 추가되어진다. 이때 검정색 노드가 두 개가 붙어있는 상태를 doubly black 이라고 말한다.
만약 반대로 삭제된 노드의 자리가 NIL과 같은 검정색 노드가 아닌 빨간색 노드가 위치해 있고, 이 위치에 extra black이 붙게 되면, 이 상태는 red and black이라고 말한다.
red and black인 경우에는 해당 노드를 검정색 노드로 변경하면 마무리가 되지만, doubly black의 경우에는 조금 더 복잡한 과정을 거쳐야 한다.
doubly black을 해결하기 위한 경우는 크게 4가지로 나뉘어 진다.
case 1) doubly black의 형제 노드가 빨간색인 경우
- doubly black의 형제와 부모의 색을 바꾼다
- 부모를 기준으로 왼쪽 회전 한다 (doubly black의 형제가 부모 기준으로 오른쪽에 있는 경우를 의미한다. 왼쪽에 있는 경우는 오른쪽 회전을 수행한다)
- 이후 doubly black의 위치에서 case 2, 3, 4를 수행한다.
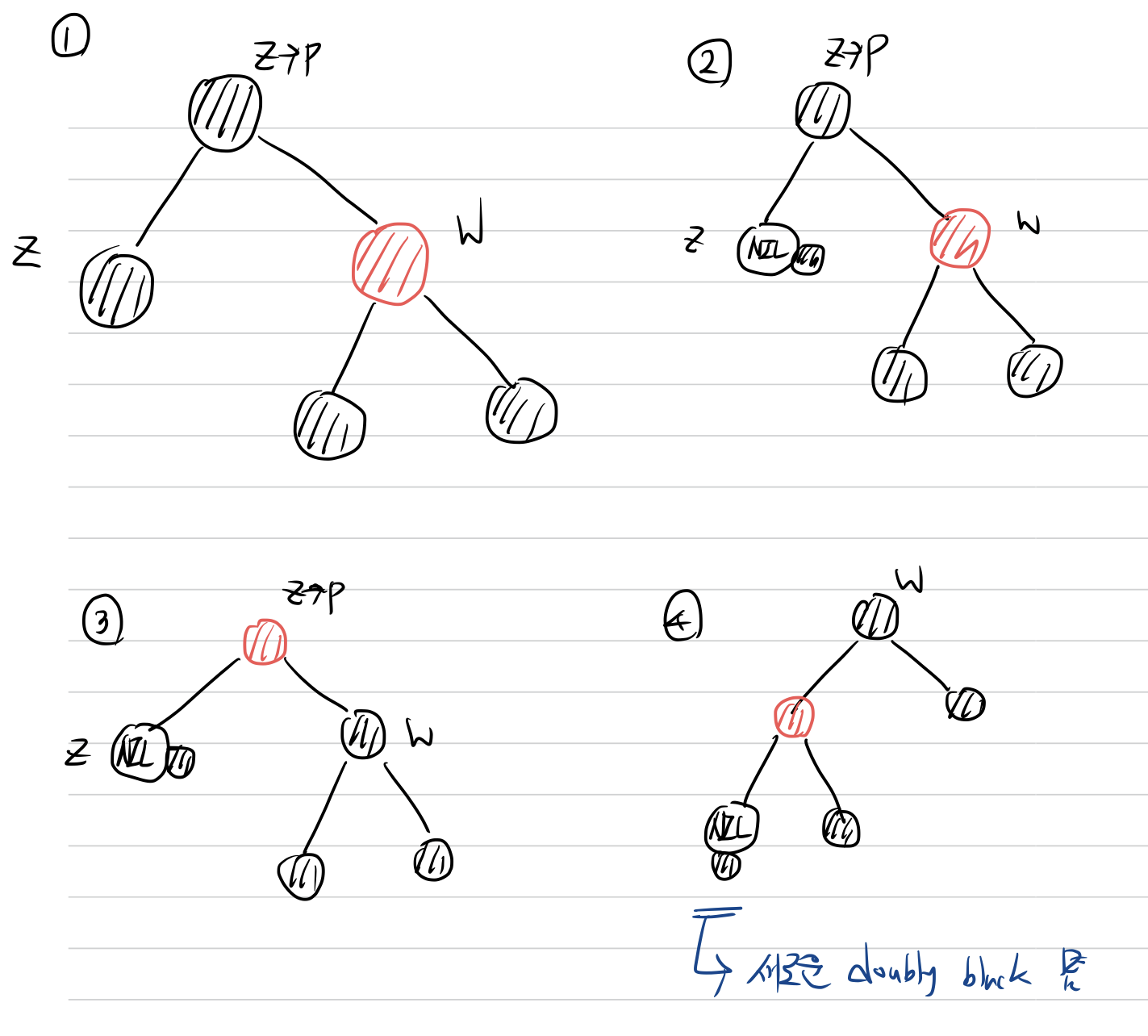
그림에서 삭제하려고 하는 노드는 z이고 자식이 없으므로 z 스스로가 삭제되는 노드가 된다. 따라서 z가 지워지고 NIL이 된다. 이후 extra black이 추가 되므로 z는 doubly black이 된다.
doubly black이 되었으므로 형제 노드인 w의 색깔을 확인한다. w의 색깔이 빨간색이므로 case 1)에 해당하게 된다. 따라서 위의 case 1) 문제 해결 순서에 따라 문제를 해결하면 위 그림과 같은 과정을 수행하게 된다.
case 2) doubly black의 형제 노드가 검정색이고, 형제의 두 자식이 모두 검정색일 경우
- doubly black과 형제의 black을 모아서 부모에게 전달한다.
- doubly black은 black 1개만 남게 되고, 원래 black 한 개였던 형제는 black을 빼앗겨 red가 된다.
- 그렇다면 부모는 red and black 또는 doubly black이 되었을 것이다.
- red and black 이라면 black으로 변경한다
- doubly black 인데 root 노드 라면 black으로 변경한다
- doubly black 인데 root 노드가 아니라면, case 1, 2, 3, 4와 비교하여 다시 균형을 조정한다
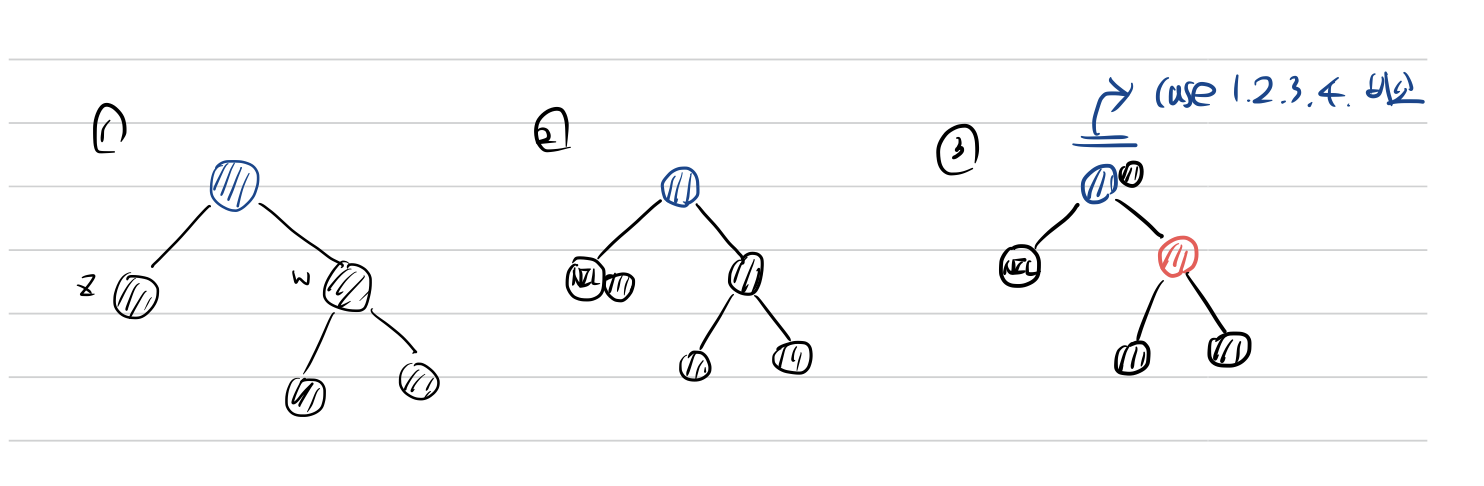
그림에서 삭제하려고 하는 노드는 z이고 자식이 없으므로 z 스스로가 삭제되는 노드가 된다. 따라서 z가 지워지고 NIL이 된다. 이후 extra black이 추가 되므로 z는 doubly black이 된다.
doubly black이 되었으므로 형제 노드인 w의 색깔을 확인한다. w의 색깔이 검정색이므로 자식의 색깔을 확인하게 된다. 오른쪽과 왼쪽 모두 검정색 노드 이므로 case 2)에 해당함을 확인할 수 있다. 따라서 case 2) 문제 해결 순서에 따라 문제를 해결하면 위 그림과 같은 과정을 수행하게 된다.
case 3) doubly black의 오른쪽 형제 노드가 검정색이고 형제의 왼쪽 자식 노드가 빨간색인 경우(왼쪽 형제일 경우 오른쪽 자식 노드가 빨간색인 경우)
이 경우에는 아래 그림에서 보이는것과 같이 doubly black 형제의 red인 자식의 위치가 doubly black의 형제와 그 부모의 위치와 비교하였을때, 일직선상에 오지 않고 꺾여있는 상태가 되어있음을 확인할 수 있다. 이 경우에는 doubly black 형제의 왼쪽에 위치한 red인 자식이 오른쪽 자식으로 올 수 있도록 변경해준다. 그 과정은 다음과 같다.
- doubly black의 형제 노드와 그 왼쪽 자식인 red 노드의 색깔을 변경한다.
- 이후 doubly black의 형제 노드를 기준으로 오른쪽 회전을 시킨다.
- 그렇다면 case 4)와 같은 상태가 되고, 이후 case 4)의 해결 과정에 따라 균형을 조정한다.
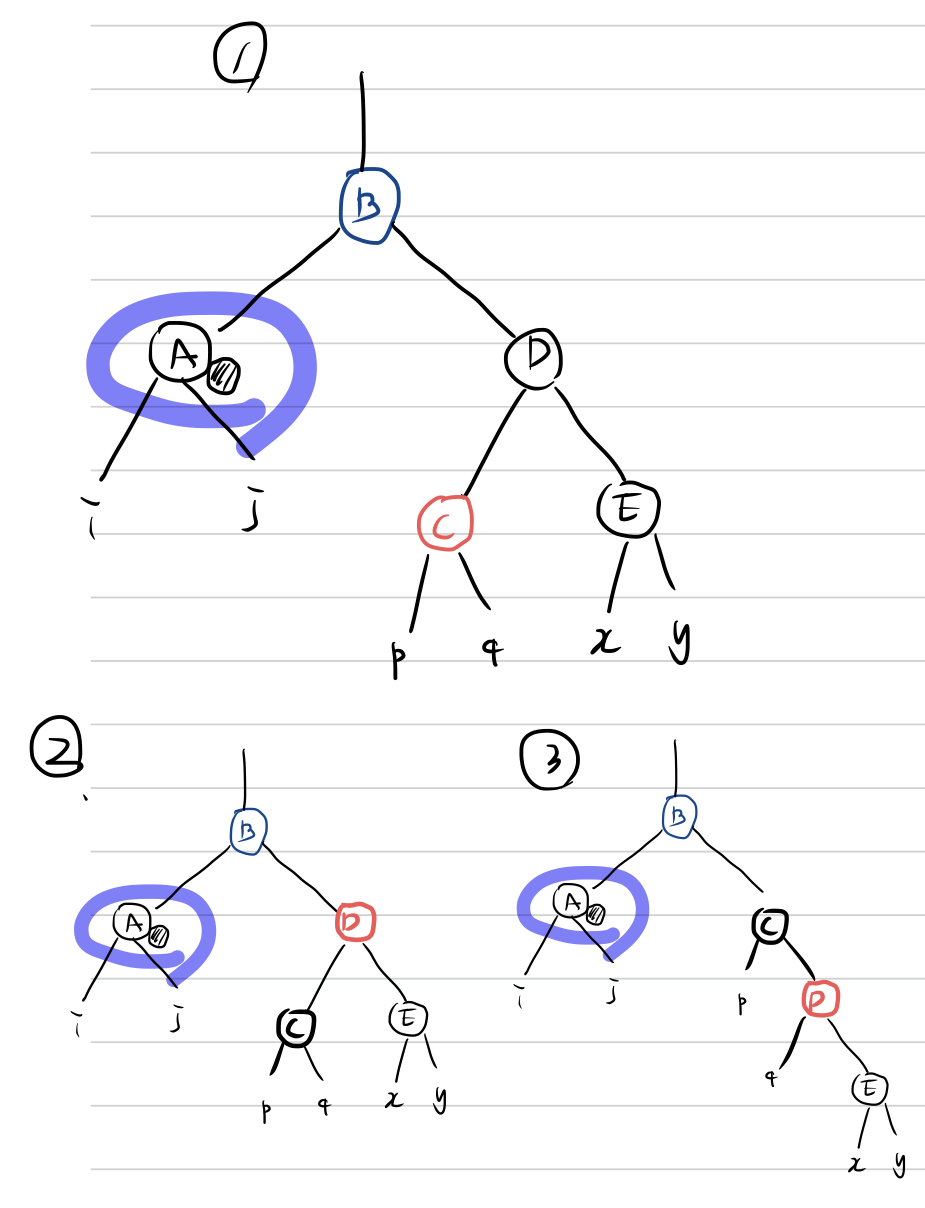
case 4) doubly black의 오른쪽 형제의 형제의 오른쪽 노드가 빨간색인 경우(왼쪽 형제일 경우 오른쪽 자식 노드가 빨간색인 경우)
- doubly black의 형제의 오른쪽 자식 노드의 색을 red -> black 으로 변경한다.
- doubly black의 형제의 색을 부모의 색깔로 변경한다.
- doubly black의 부모의 색깔을 black으로 변경한다.
- 부모를 기준으로 왼쪽 회전을 수행한다.
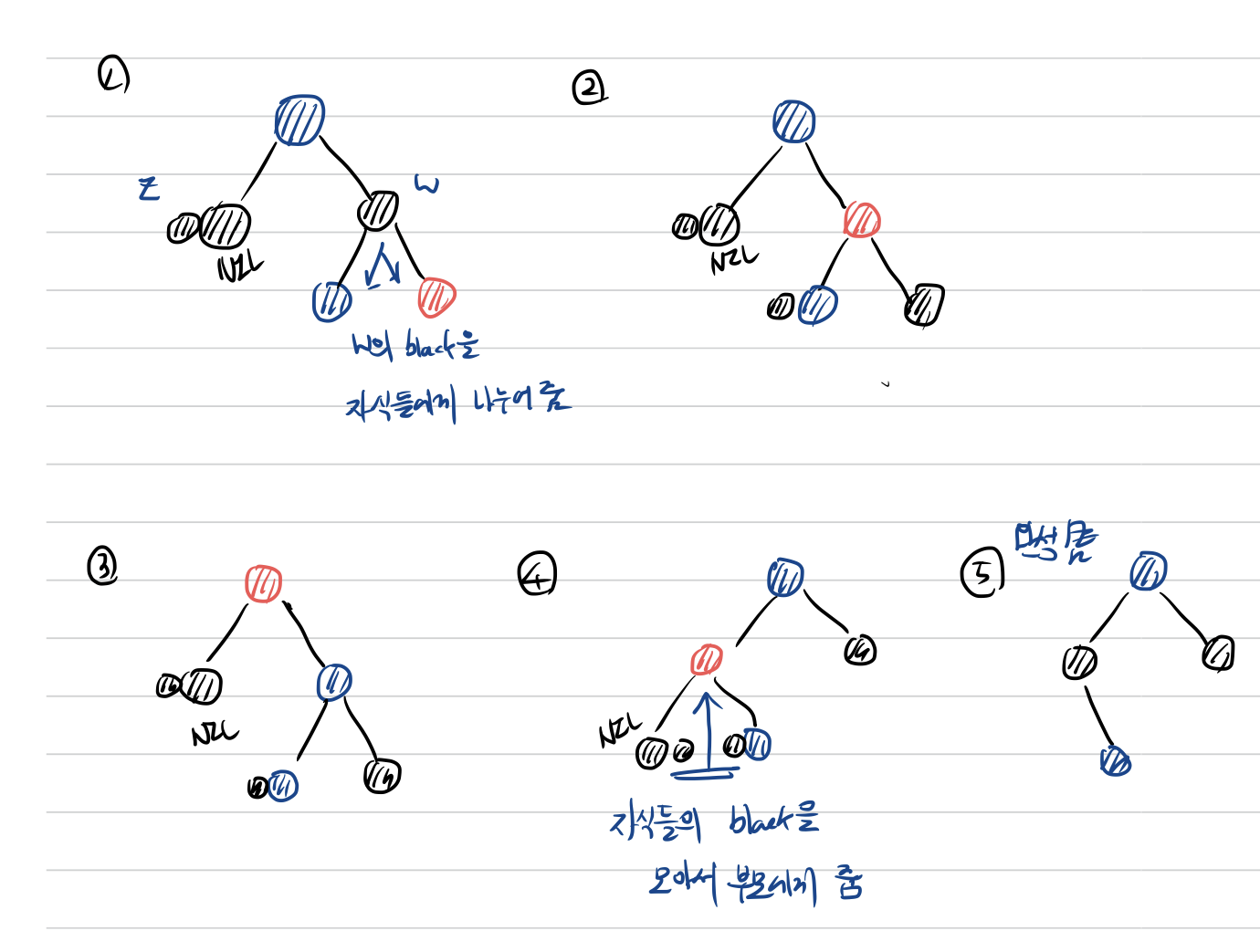
위 과정은 결과론적인 관점에서 축약된 과정이며 실제 세부 과정은 아래 그림과 같다. 아래 그림 기준에서의 과정에 대한 설명은 다음과 같다. (그림에서 파란색 노드는 red 인지 black 인지 확인되지 않은 노드이다)
- doubly black의 형제 노드의 black을 두 자식들에게 나누어 준다.
- 형제의 두 자식들은 각각 extra black 노드를 받게 되고 2번 그림과 같은 상태가 된다. (파란색 노드는 색깔을 모르므로 파란색 옆에 extra black으로 표현했고, red는 red and black 이 되므로 black으로 바로 변경해준 모습이다)
- doubly black의 형제 노드와 그 부모의 색을 바꾸어 준다.
- 부모 노드를 기준으로 왼쪽 회전을 수행한다. 그렇게 되면 4번 그림과 같은 상태가 되고, red의 두 자식이 extra black을 가지고 있는 상태가 된다. 이 두 자식의 extra black을 모아서 부모인 red노드에게 전달해주게 된다.
- 최종적으로 5번 그림과 같은 상태가 되어 5번 조건을 만족하게 된다. (5번 그림에서 red의 왼쪽 자식이 extra black을 빼앗기고 사라진 이유는 본래 extra black 이 없다면 NIL 노드이기 때문에, 그림에서 생략한 것이다)
이를 c로 구현한 코드는 아래와 같다.
전체 코드 : https://github.com/saint6839/jungle-week-05
회전 함수
// x가 부모이고 y가 오른쪽 노드일때 y를 부모로 바꾸고 x를 왼쪽 노드로 회전 시키는 함수
void left_rotate(rbtree *t, node_t *x)
{
node_t *y = x->right; // x의 오른쪽 노드의 주소를 선언함
x->right = y->left; // y의 왼쪽 노드를 x의 오른쪽으로 옮김
if (y->left != t->nil)
{ // 만약 y의 왼쪽 노드가 NIL이 아니라면,
y->left->parent = x; // 기존 y의 왼쪽에 있던 노드의 parent 노드를 x로 맞추어준다.
}
y->parent = x->parent; // x의 자리에 y가 올라왔으므로, 기존 x의 부모를 y의 부모로 바꾸어준다.
if (x->parent == t->nil)
{ // 만약 x의 부모가 NIL 이라면, root 노드라는 의미이므로,
t->root = y; // y를 트리의 root로 선언한다.
}
else if (x == x->parent->left)
{ // 만약 x가 회전 되기 전에 부모의 왼쪽에 위치한 노드였다면,
x->parent->left = y; // x부모의 왼쪽을 y로 바꾸어준다.
}
else
{ // 아니라면, x가 회전 되기 전에 부모의 오른쪽에 위치했다는 의미이므로,
x->parent->right = y; // x부모의 오른쪽을 y로 바꾸어준다.
}
y->left = x; // y의 왼쪽을 x로 바꾸어준다.
x->parent = y; // x의 부모를 y로 바꾸어준다.
}
// y가 부모이고 x가 왼쪽 노드일때 x를 부모로 바꾸고 y를 오른쪽 노드로 회전 시키는 함수
void right_rotate(rbtree *t, node_t *y)
{
node_t *x = y->left; // y의 왼쪽 노드를 선언함
y->left = x->right; // x의 오른쪽 노드를 y의 왼쪽으로 옮겨줌
if (x->right != t->nil)
{ // x의 오른쪽이 NIL이 아니라면,
x->right->parent = y; // 기존 x의 오른쪽에 있었던 노드의 parent 노드를 y로 맞추어준다.
}
x->parent = y->parent; // y의 자리에 x가 올라왔으므로, 기존 y의 부모를 x의 부모로 바꾸어준다.
if (y->parent == t->nil)
{ // 만약 y의 부모가 NIL 이라면, root 노드라는 의미이므로,
t->root = x; // x를 트리의 root로 선언한다.
}
else if (y == y->parent->left)
{ // 만약 y가 회전 되기 전에 부모의 왼쪽에 위치한 노드였다면,
y->parent->left = x; // y부모의 왼쪽을 x로 바꾸어준다.
}
else
{ // 아니라면, y가 회전 되기 전에 부모의 오른쪽에 위치했다는 의미이므로,
y->parent->right = x; // y부모의 오른쪽을 x로 바꾸어준다.
}
x->right = y; // x의 오른쪽을 y로 바꾸어준다.
y->parent = x; // y의 부모를 x로 바꾸어준다.
}삭제 함수
// u노드의 위치를 v노드로 교체해주는 함수
void rbtree_transplant(rbtree *t, node_t *u, node_t *v)
{
if (u->parent == t->nil)
{
t->root = v;
}
else if (u == u->parent->left)
{
u->parent->left = v;
}
else
{
u->parent->right = v;
}
v->parent = u->parent;
}
void *rbtree_erase_fixup(rbtree *t, node_t *x)
{
node_t *w;
while (x != t->root && x->color == RBTREE_BLACK) // x가 root가 아니고, x의 색이 BLACK일 동안
{
if (x == x->parent->left) // doubly black인 x가 왼쪽 자식일 경우
{
w = x->parent->right; // w는 x의 형제 노드
if (w->color == RBTREE_RED)
{ // x의 오른쪽 형제 w가 RED인 경우 -> case 1) doubly black의 형제가 RED인 경우에 해당
w->color = RBTREE_BLACK; // 형제의 색을 BLACK으로 변경하고
x->parent->color = RBTREE_RED; // 형제의 부모의 색을 RED로 변경한다.
left_rotate(t, x->parent); // 부모를 기준으로 왼쪽 회전 수행
w = x->parent->right; // x의 위치가 바뀌었으므로, x의 형제인 w의 위치 또한 갱신해줌
} // 이후 경우1은 경우 2,3,4 중 하나로 변환 되었음
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK) // 형제의 자식이 모두 BLACK일 경우 case 2) doubly black의 형제의 자식이 모두 BLACK일 경우에 해당
{
w->color = RBTREE_RED; // 형제의 검은색을 부모에게 주므로 기존 BLACK에서, RED로 변함
x = x->parent; // x의 부모가 x의 extra black을 물려받아, 새로운 red and black 또는 doubly black이 됨
}
else // 형제의 자식 중 RED인 자식이 있을 경우 case 3)에 해당, 회전을 통해 case 4)로 변경해주어야함
{
if (w->right->color == RBTREE_BLACK) // 형제 자식의 오른쪽 노드가 BLACK이고, 왼쪽 노드가 RED일 경우
{
w->left->color = RBTREE_BLACK; // 형제의 왼쪽 노드를 RED -> BLACK으로 변경
w->color = RBTREE_RED; // 형제의 색깔을 BLACK -> RED로 변경
right_rotate(t, w); // 오른쪽 회전 시켜서 꺾이지 않도록 함
w = x->parent->right; // x의 위치가 바뀌었으므로, x의 형제인 w의 위치 또한 갱신해줌
}
// case 4)에 해당
w->color = x->parent->color; // 형제의 색을 부모의 색으로 변경
x->parent->color = RBTREE_BLACK; // 부모의 색을 BLACK으로 변경
w->right->color = RBTREE_BLACK; // 형제의 오른쪽 자식의 색을 BLACK으로 변경
left_rotate(t, x->parent); // 왼쪽 회전 시킴
x = t->root;
}
}
else // doubly black인 x가 오른쪽 자식일 경우
{
w = x->parent->left; // w는 x의 형제 노드
if (w->color == RBTREE_RED)
{ // 형제의 색깔이 RED인 경우 -> case 1)에 해당
w->color = RBTREE_BLACK; // 형제의 색을 BLACK으로 변경한다.
w->parent->color = RBTREE_RED; // 형제의 부모의 색을 RED로 변경한다.
right_rotate(t, x->parent); // 부모를 기준으로 오른쪽 회전 수행
w = x->parent->left; // x의 위치가 바뀌었으므로, x의 형제인 w의 위치 또한 갱신해준다.
} // 이후 경우1은 경우 2,3,4 중 하나로 변환 되었음
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK) // case 2)에 해당
{
w->color = RBTREE_RED; // 형제의 검은색을 부모에게 주므로 기존 BLACK에서, RED로 변함
x = x->parent; // x의 부모가 x의 extra black을 물려받아, 새로운 red and black 또는 doubly black이 됨
}
else // 형제의 자식 중 RED인 자식이 있을 경우 case 3)에 해당, 회전을 통해 case 4)로 변경해주어야함
{
if (w->left->color == RBTREE_BLACK) // 형제의 자식의 오른쪽 자식 색깔이 RED인 경우 -> 오른쪽 자식이 red인 상태에서 왼쪽 자식이 red인 상태로 바꾸어 준다.
{
w->right->color = RBTREE_BLACK; // 형제 오른쪽 노드를 RED -> BLACK
w->color = RBTREE_RED; // 형제 색깔을 BLACK -> RED
left_rotate(t, w); // 왼쪽으로 회전
w = x->parent->left; // x의 위치가 바뀌었으므로, x의 형제인 w의 위치 또한 갱신해줌
}
// 형제의 자식의 왼쪽 노드의 자식 색깔이 RED인 경우 case 4)에 해당
w->color = x->parent->color; // 형제의 색을 부모의 색으로 변경
x->parent->color = RBTREE_BLACK; // 부모의 색을 BLACK으로 변경
w->left->color = RBTREE_BLACK; // 형제의 왼쪽 자식의 색을 BLACK으로 변경
right_rotate(t, x->parent); // 오른쪽 회전 시킴
x = t->root;
}
}
}
x->color = RBTREE_BLACK;
}
int rbtree_erase(rbtree *t, node_t *z)
{
node_t *y = z; // z는 삭제 대상의 주소 값, y는 자식 갯수에 따라서 그대로 z가 될 수도 있고, z의 successor의 주소가 될 수도 있다.
node_t *x; // y의 원래 위치로 이동시키는 용도의 노드 x. y의 오른쪽 자식 또는 자식이 없을 경우 t->nil 로 설정된다.
color_t y_original_color = y->color; // y의 색깔은 변경될 가능성이 존재하므로, 미리 새로운 변수에 y의 원래 색깔을 저장해둔다.
if (z->left == t->nil)
{ // z의 왼쪽 노드가 없다면
x = z->right; // z의 오른쪽 노드를 x로 선언한다.
rbtree_transplant(t, z, z->right); // z의 오른쪽 노드를 z의 자리에 교체한다.
}
else if (z->right == t->nil)
{ // z의 오른쪽 노드가 없다면
x = z->left;
rbtree_transplant(t, z, z->left); // z의 왼쪽 노드를 z의 자리에 교체한다.
}
else // z의 자식 노드가 둘 다 있을 경우
{
y = tree_minimum(t, z->right); // z의 오른쪽 서브트리의 successor를 찾는다.
y_original_color = y->color;
x = y->right;
if (y->parent == z)
{ // 만약 z의 오른쪽 서브트리의 successor가 z의 오른쪽 노드라면
x->parent = y; // x의 부모를 y로 선언
}
else
{
rbtree_transplant(t, y, y->right); // z에 z의 successor인 y를 이식하기 전에, y의 자리에 y의 자식을 이식 시켜둔다. (그렇지 않으면, y는 자식이 달려 있는 상태로 z에 이식되기 때문이다)
y->right = z->right; // z 자리에 y를 이식하기 전, y의 오른쪽 자식을 z의 오른쪽 자식으로 교체
y->right->parent = y; // z자리에 y를 이식하기 전, y의 오른쪽 자식의 부모 노드를 y로 교체
}
rbtree_transplant(t, z, y); // z의 자리에 y를 이식한다.
y->left = z->left; // z의 왼쪽 자식이 y의 왼쪽 자식이 된다.
y->left->parent = y; // z의 왼쪽 자식의 부모가 곧, y가 된다.
y->color = z->color; // y가 z의 자리에 이식되고, y는 z의 색깔만 물려 받는다(값은 본래 y의 값 유지)
}
// 만약 삭제 대상의 색깔이 BLACK이라면, 각 경로의 BLACK 노드의 갯수의 균형이 깨지게 되므로, 균형을 맞춰 주어야 한다.
if (y_original_color == RBTREE_BLACK)
{
rbtree_erase_fixup(t, x);
}
free(z); // z가 삭제 되었으므로, z의 메모리 주소를 비워준다.
return 0;
}

굿