[JAVA] 이분탐색

참고: [바킹독의 실전 알고리즘] 0x13강 - 이분탐색

중복되는 수 중 가장 작은 인덱스 값 찾기

public static int lowerBound(int target, int[] arr) {
    int l = 0;
    int r = arr.length - 1;
    
    while (l < r) {
        int m = (l + r) / 2;
        if (arr[m] >= target) r = mid;
        else l = m + 1;
    }
    return l;
}

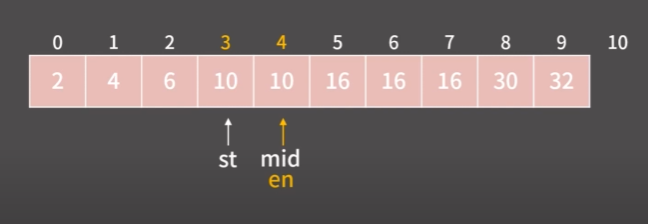
• arr[m]이 원하는 값보다 크거나 작을 때 계속해서 왼쪽으로 움직인다.
• 결국 마지막에 st, mid, en의 값이 3에서 동시에 멈추는 순간이 오게 된다.

중복되는 수 중 가장 큰 인덱스 값 찾기

public static int upperBound(int target, int[] arr) {
    int l = 0;
    int r = arr.length - 1;
    
    while (l < r) {
        int m = (l + r) / 2;
        if (arr[m] > target) r = mid;
        else l = m + 1;
    }
    return l;
}

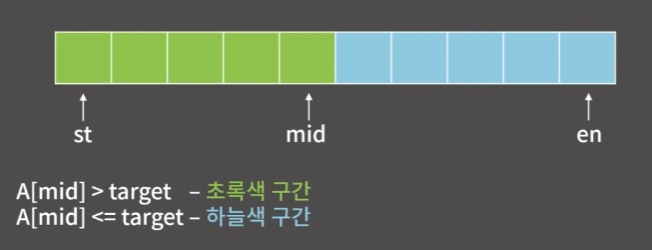
• arr[m] == target일 때 하늘색 구간이 된다.
• 가장 오른쪽 위치는 target보다 큰 수가 최초로 나온 위치이다.

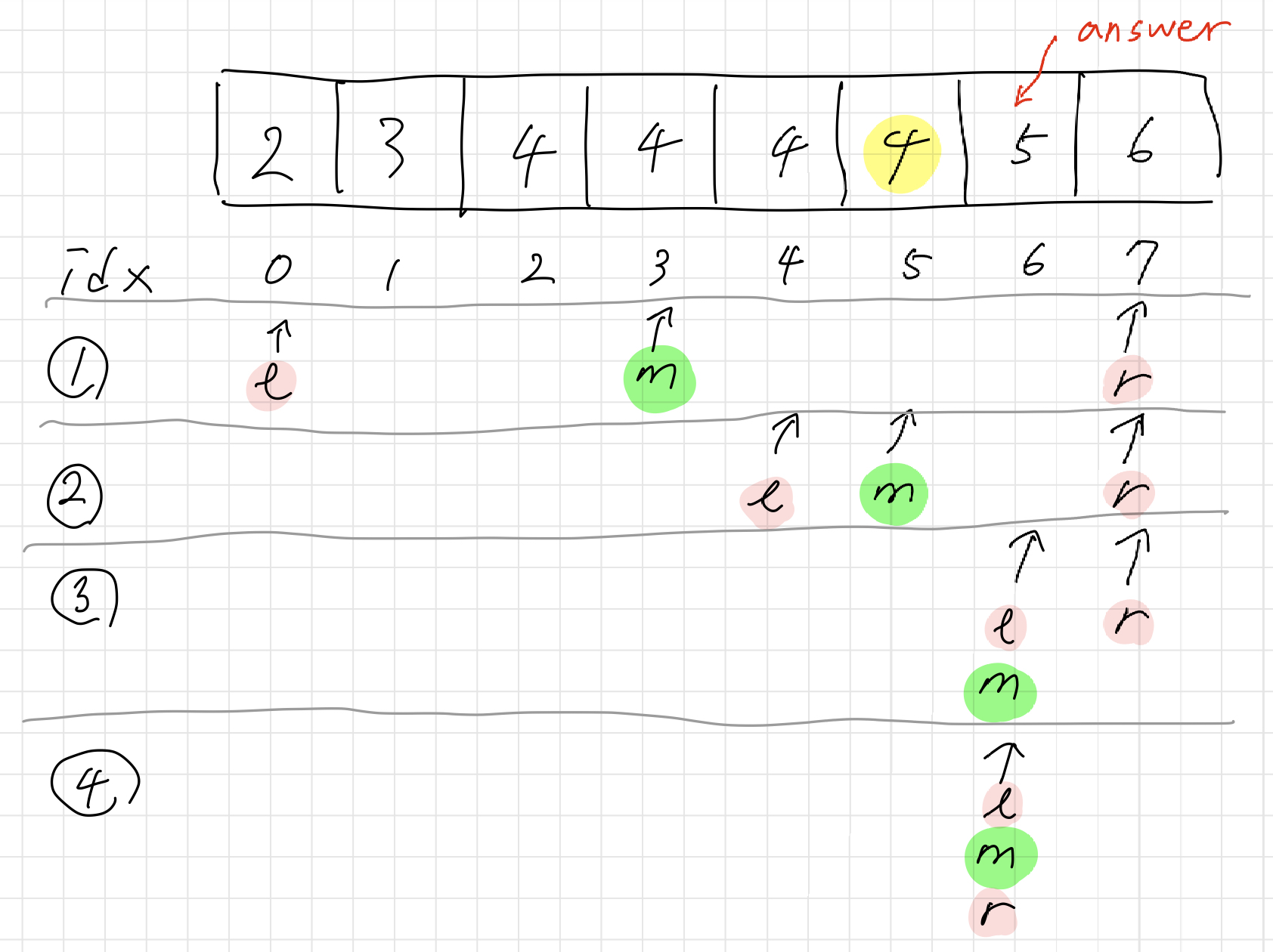
• l은 target보다 작거나 같을 때 계속해서 오른쪽 구간으로 움직인다(건너간다).
• 마지막에 r은 target보다 큰 수가 최초로 나온 위치(l)로 움직인다.
• 이후 l, m, r은 동시에 한 위치에서 멈춘다.

주의사항

• 첫 l, r 설정이 중요한 이유?
  - 첫 구간이 잘못 설정되면 적절한 mid값을 선택하지 못하여 구간을 반반으로 잘 가르지 못하는 현상이 발생하게 된다
  - 이런 경우 프로그램이 무한루프에 빠지는 현상이 발생할 수 있다
  - 직접 이분탐색을 짤 때 무한루프가 발생한다면 l과 r이 1 차이 날 때 무슨 일이 일어나는지 주의깊게 살펴보자.