[JAVA] 분할정복

참고: https://www.tutorialspoint.com/data_structures_algorithms/divide_and_conquer.htm

분할정복 알고리즘

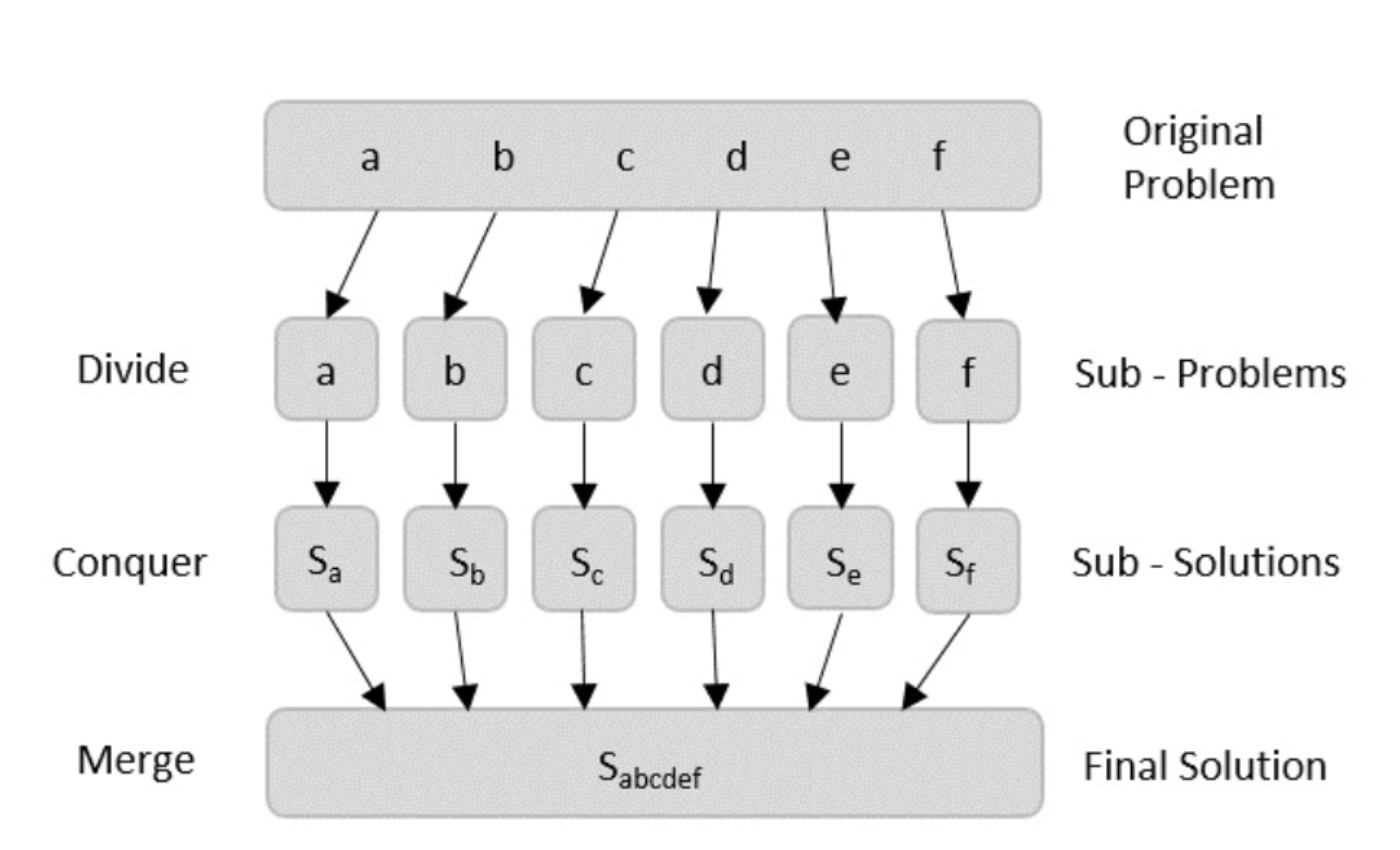
분할 정복이란 문제를 더 이상 나눌 수 없는 단위까지 쪼갠 후 그 하위 문제들의 답을 이용하여 원래 문제의 답을 도출하는 것을 말한다. 분할 정복의 과정은 대략 3단계로 나눌 수 있다.

Divide / Break

이 단계에서는 문제를 하위 문제로 쪼갠다. 이 하위 문제는 원본 문제를 대표할 수 있어야 한다. 쪼개는 과정은 일반적으로 재귀를 사용한다.

Conquer / Solve

위 단계에서 원자 단위로 나누어 놓았던 하위 문제의 해를 도출한다.

Merge / Combine

하위 문제들의 해를 도출한 후에는 다시 재귀적으로 이 해들을 병합하여 원본 문제의 답을 도출할 수 있도록 한다.

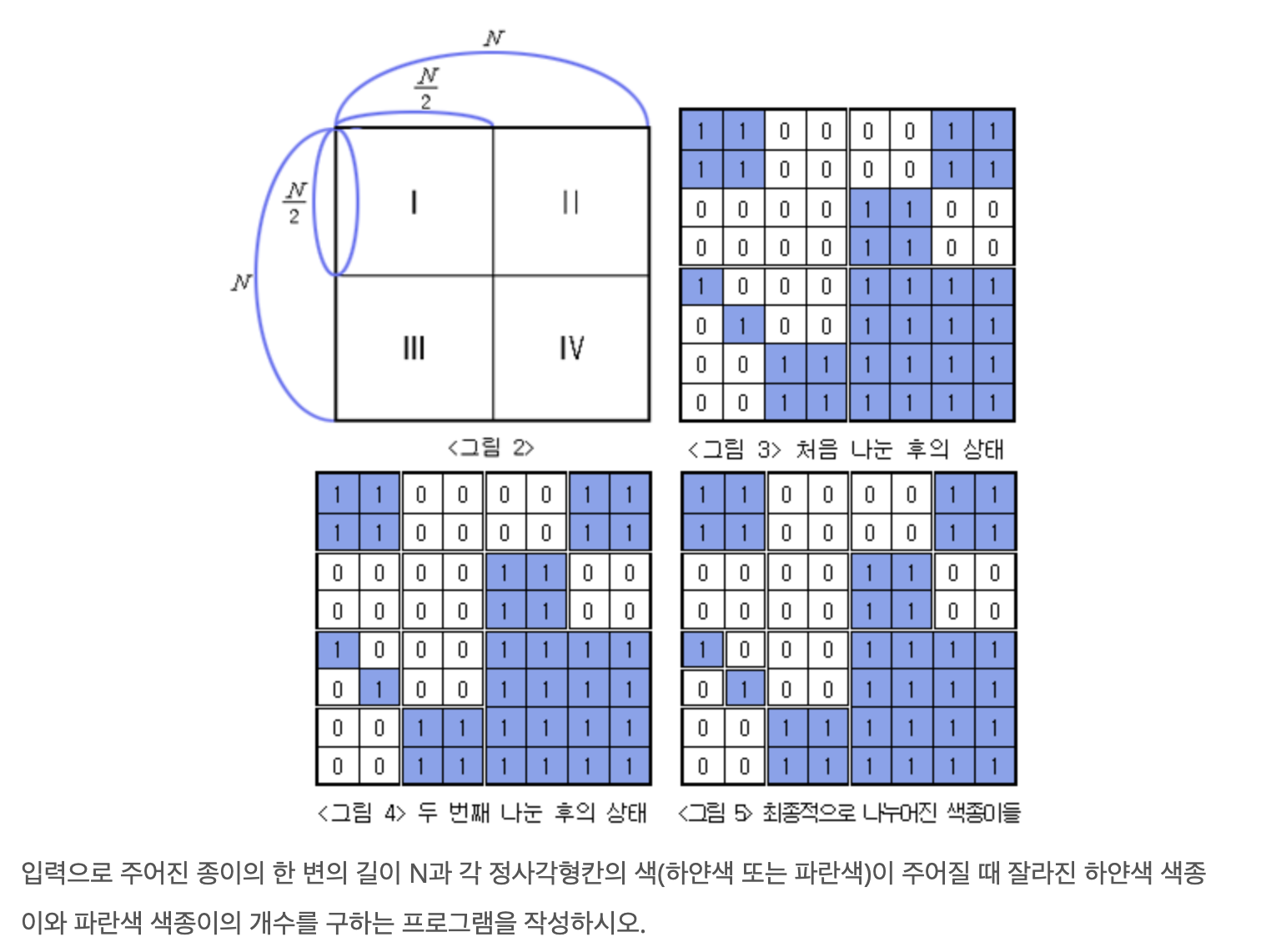
백준 2630 색종이 만들기

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class B_S2_2630 {
    static int N;
    static int white;
    static int blue;
    static int[][] map;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        N = Integer.parseInt(br.readLine());
        map = new int[N][N];

        for (int i = 0; i < N; i++) {
            String[] temp = br.readLine().split(" ");
            for (int j = 0; j < N; j++) {
                map[i][j] = Integer.parseInt(temp[j]);
            }
        }

        white = 0;
        blue = 0;
        isFull(0, 0, N);

        System.out.printf("%d\n%d", white, blue);
    }

    static void cutPaper(int r, int c, int size) {
        int piece = size / 2;
        isFull(r, c, piece);
        isFull(r + piece, c, piece);
        isFull(r, c + piece, piece);
        isFull(r + piece, c + piece, piece);
    }

    static void isFull(int r, int c, int size) {
        if (size == 1) {
            if (map[r][c] == 1) blue++;
            else white++;
            return;
        }

        int curr = map[r][c];

        for (int i = r; i < r + size; i++) {
            for (int j = c; j < c + size; j++) {
                if (map[i][j] != curr) {
                    cutPaper(r, c, size);
                    return;
                }
            }
        }

        if (curr == 1) blue++;
        else white++;
    }
}

일단 되는 대로 풀어본 코드인데, 얼기설기 코드를 엮어 답을 도출한 후에도 문제가 돌아가는 전체적인 과정을 명확히 이해할 수 없었다. 위에서 정리한 내용을 바탕으로 코드를 다시 읽으며 발견한 패턴은 바로 분할하는 함수와 정복하는 함수를 나누어 썼다는 것이다.

• cutPaper 함수: 종이를 size에 맞추어 4등분, 즉 분할하는 함수이다
• isFull 함수: 분할된 종이가 atomic한 단위까지 나뉘어 있는지 검사한 후 나뉘어 있다면 해를 도출하고, 그렇지 않다면 다시 cutPaper 함수를 호출하여 종이를 분할시키는 함수다. 즉 정복하는 함수다. 또한 이 함수에서 병합이 이루어지고 있기도 하다.

재귀 함수 두 개가 서로 엮여서 움직이고 있는 상황이 내가 만들었으면서도 참 낯설게 다가왔다. 그래서 비슷한 문제를 하나 더 풀어보았다.

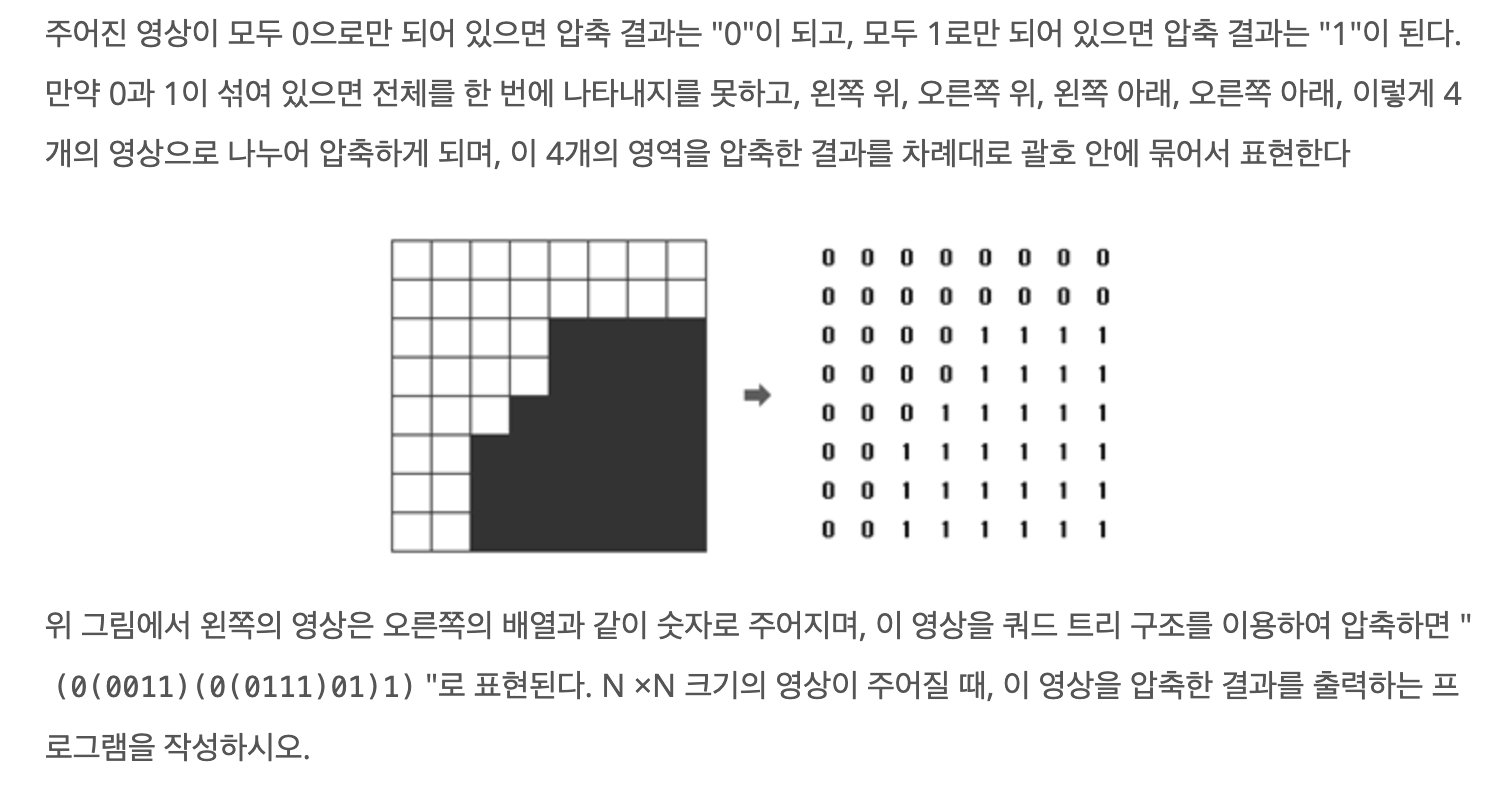
백준 1992 쿼드트리

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class B_S1_1992 {
    static int[][] map;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        map = new int[N][N];
        for (int i = 0; i < N; i++) {
            String s = br.readLine();
            for (int j = 0; j < N; j++) {
                map[i][j] = Integer.parseInt(String.valueOf(s.charAt(j)));
            }
        }
        String ans = inspect(0, 0, N);
        System.out.println(ans);
    }

    static String zip(int r, int c, int size) {
        int cut = size / 2;
        StringBuilder sb = new StringBuilder();
        sb.append('(');
        sb.append(inspect(r, c, cut));
        sb.append(inspect(r, c + cut, cut));
        sb.append(inspect(r + cut, c, cut));
        sb.append(inspect(r + cut, c + cut, cut));
        sb.append(')');
        return sb.toString();
    }

    static String inspect(int r, int c, int size) {
        int curr = map[r][c];
        for (int i = r; i < r + size; i++) {
            for (int j = c; j < c + size; j++) {
                if (map[i][j] != curr) {
                    return zip(r, c, size);
                }
            }
        }
        return String.valueOf(curr);
    }
}

해당 코드에서도 마찬가지로 분할하는 함수와 정복하는 함수가 따로 작성이 되어있다.

• zip: 배열을 4분할하고있다.
• inspect: 현재 검사하는 배열이 atomic 단위인지 검사하고 그렇지 않다면 다시 zip 함수를 호출하여 4등분한다. 만약 atomic 단위라면 현재의 값을 반환한다.

물론 이렇게 분할하는 함수와 정복하는 함수를 꼭 따로 써야하는 것은 아니다. 다른 사람들의 코드를 읽어보면 함수 하나로도 잘 구현이 되어있다.

다만 분할정복이 아직도 너무 낯설게 느껴지고 전개 과정이 머릿속에 선명하게 그려지지 않아 당분간 이렇게 단계를 나누어 생각하는 것이 좋을 것 같다.