이번 글에서는 추상 자료형(ADT: Abstract Data Type) 중 하나인 Heap에 대해 알아봅니다.

Heap

힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(complete binary tree)를 기본으로 한 자료구조(tree-based structure)로서 부모 노드와 자식 노드의 키값이 대소관계가 성립한다.

• 새로운 값을 넣어주거나 기존 값을 빼주면 대소관계에 따라 값을 재배열하며 이때의 시간 복잡도는 $O(\log n)$이다.

• 종류에 따라 최댓값 혹은 최솟값이 항상 Root에 위치한다.

Max Heap

부모노드의 키값이 자식노드의 키값보다 항상 큰 힙

• Max Heap의 최댓값은 Root에 위치하기 때문에 $O(1)$의 시간 복잡도로 접근이 가능

Min Heap

부모노드의 키값이 자식노드의 키값보다 항상 작은 힙

• Min Heap의 최솟값은 Root에 위치하기 때문에 $O(1)$의 시간 복잡도로 접근이 가능

Heap-pop

Root에 위치한 최솟값 혹은 최댓값을 빼주는 것

• 이때 공석이된 Root에는 가장 마지막 요소(element)를 넣어준 후 대소관계에 따라 재배열하며 $O(\log n)$의 시간 복잡도를 갖는다.

Index

• Array에서는 완전 이진 트리의 Root 위치에서부터 자식 노드 순서대로 각 값이 인덱스 번호를 갖는다.
  • 이때, Root는 항상 최솟값 혹은 최댓값이지만 그 다음 인덱스가 Root를 제외한 최솟값 혹은 최댓값이라는 것을 의미하지는 않는다.

[예시]

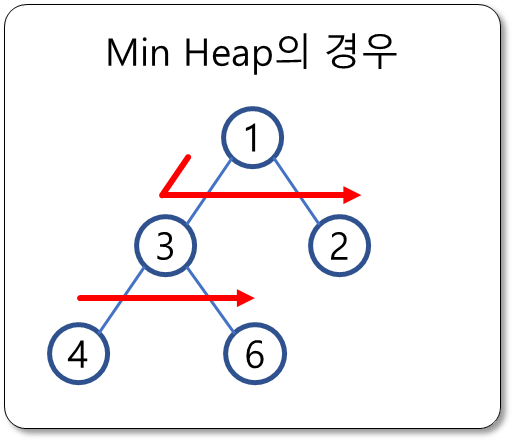
• 위의 예시를 Array로 표현하면 다음과 같다.

  $[1, 3, 2, 4, 6]$

Parent Index

$\dfrac{idx - 1}{2}$

• 현재 index에서 1을 빼고 2로 나누면 부모 노드의 인덱스 값이다.
  • 이때, 소수점 이하자리는 버림.

Left Child Index

$2 \cdot idx + 1$

Right Child Index

$2 \cdot idx + 2$

heapq Module

• 파이썬 내장 모듈 heapq을 이용하여 간단히 힙 자료구조를 사용할 수 있다.

heapify()

• 기존의 리스트를 heap 자료구조 형태로 만들어 주는 함수

[입력 예시]

from heapq import heapify

example = [1, 5, 4, 3, 2]

heapify(example)
print(example)

[출력 예시]

[1, 2, 4, 3, 5]

heappush()

• heappush(<Target>, <item>): <Target>에 <item>을 힙 방식으로 추가한다.

[입력 예시]

from heapq import heappush

example = []
heappush(example, 5)
heappush(example, 3)
heappush(example, 1)
heappush(example, 2)
heappush(example, 4)

print(example)

[출력 예시]

[1, 2, 3, 5, 4]

heappop()

• heappop(<Target>): <Target>의 0번 인덱스를 뽑아낸다.

[입력 예시]

from heapq import heappop

example = [1, 2, 3, 5, 4]

a = heappop(example)

print(a, example)

[출력 예시]

1 [2, 4, 3, 5]