1. HTTP
기본적으로 HTTP는 전송계층 위에 있는 애플리케이션 계층이며 웹서비스 통신에 사용. HTTP/1.0~HTTP/3이며 이번 포스트에서 차례로 봐볼 예정.
1-1 HTTP/1.0
한 연결당 하나의 요청 처리하도록 설계.=RTT ⬆
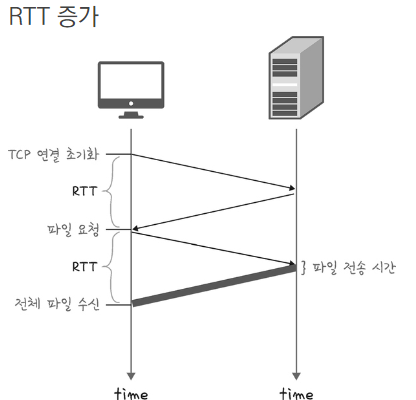
RTT 증가 = > 서버부담⬆, 사용자 응답시간 ⬆
RTT란 ?
- 패킷왕복시간 = 패킷이 목적지에 도달하고 다시 출발지로 오기까지 걸리는 시간
RTT증가를 해결하기 위한 방법
1. 이미지 스플리팅
2. 코드압축
3. 이미지 Base64인코딩
1)이미지 스플리팅
많은 이미지 다운받으면 과부하 걸림. 많은 이미지가 합쳐있는 하나의 이미지를 다운받고 이를 기반으로 background-image의 position을 이용하여 표기하는 방법
css
#icons>li>a {
background-image: url("icons.png");
width: 25px;
display: inline-block;
height: 25px;
repeat: no-repeat;
}
#icons>li:nth-child(1)>a {
background-position: 2px -8px;
}
#icons>li:nth-child(2)>a {
background-position: -29px -8px;
}위의 코드처럼 하나의 이미지 background-image: url("icons.png");, background-position 등을 기반으로 이미지를 설정.
2)코드 압축
개행문자, 띄어쓰기를 없애서 코드를 최소화 한다.
const express = require('express')
const app = express()
const port = 3000
app.get('/', (req, res) => {
res.send('Hello World!')
})
app.listen(port, () => {
console.log(`Example app listening on port ${port}`)
})위의 코드를
const express=require("express"),app=express(),port=3e3;app.get("/",(e,p)=>{p.send("Hello World!")}),app.listen(3e3,()=>{console.log("Example app listening on port 3000")});밑에처럼 압축한것.
3) 이미지Base64 인코딩
이미지 파일을 64진법으로 이루어진 문자열로 인코딩하는 기법.
서버와의 연결을 열고 이미지이에 대해 HTTP요청을 할필요x 하지만 크기가 37%정도 증가.
인코딩
정보의 형태나 형식을 표준화,보안,처리속도향상,저장 공간 절약 등을 위해 형태나 형식으로 변환하는 처리방식.
1-2. HTTP/1.1
매번 TCP연결하며 (3 way-handshake)를 하는것이 아니라 한번 TCP초기화 한 후 keep-alive라는 옵션으로 여러개의 파일을 송수신할 수 있게 바뀜. keep-alive가 1.0에서도 있었지만 표준화는 1.1부터(기본옵션)
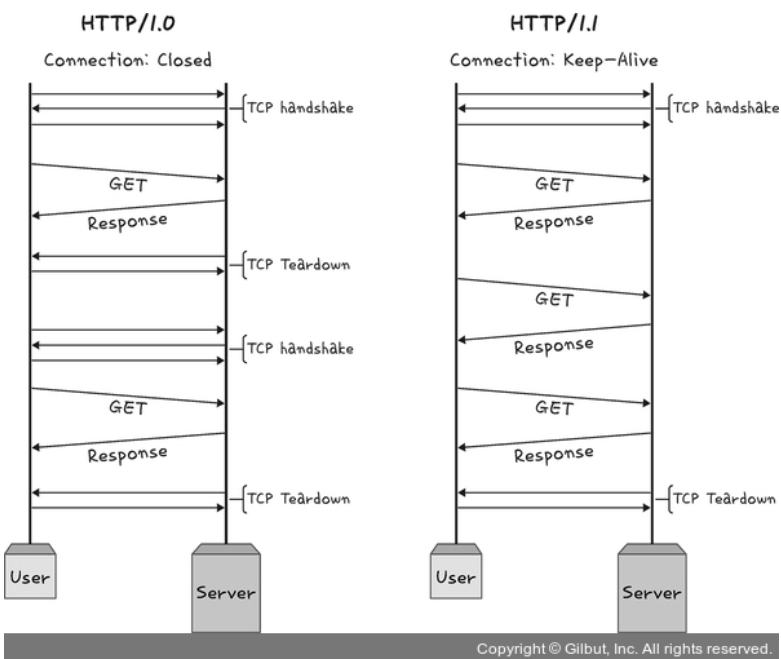
그림을 보게 되면 3way handshake가 한번 발생후 발생하지 않는걸 볼 수 있음. 리소스 갯수에 비례해 대기시간이 길어지는 단점 o.
HOL Blocking (Head Of Blocking)
같은 큐에 있는 패킷이 그 첫번째 패킷에 의해 지연될때 발생 하는 성능 저하 현상.

무거운 헤더구조
HTTP/1.1의 헤더에는 쿠키 등 많은 메타데이터가 들어있고,압축X 무거움.
1-3 HTTP/2
HTTP/2는 SPDY 프로토콜에서 파생된 HTTP/1.x보다 지연시간 ⬇ , 응답시간 ⬆
멀티플렉싱, 헤더압축,서버 푸시, 요청의 우선순위 처리지원.
SPDY 비표준 개방형 네트워크 프로토콜 HTTP헤더를 해석하고 단순화 하여 압축전송.
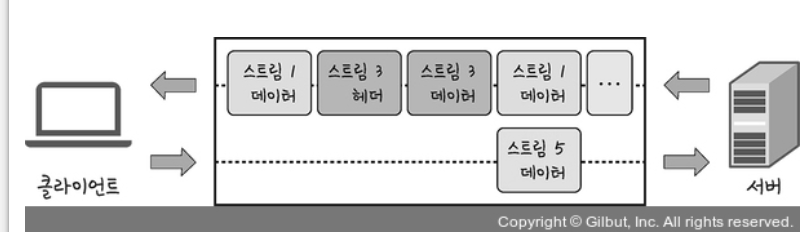
멀티플렉싱
여러개의 스트림을 사용하여 송수신 하는 것 = 특정 스트림의 패킷이 손상되어도 "해당 스트림"에만 영향을 미치고 나머지 스트림은 멀쩡동작.
스트림
시간이 지남에 따라 사용할 수 있게 되는 일련의 데이터 요소를 가리키는 데이터 흐름.
병렬적 스트림들을 통해 데이터를 서빙. 스트림 내 데이터들도 쪼개져있음. 조각내어 송수신한 이후 다시 조립하여 데이터 주고받음.
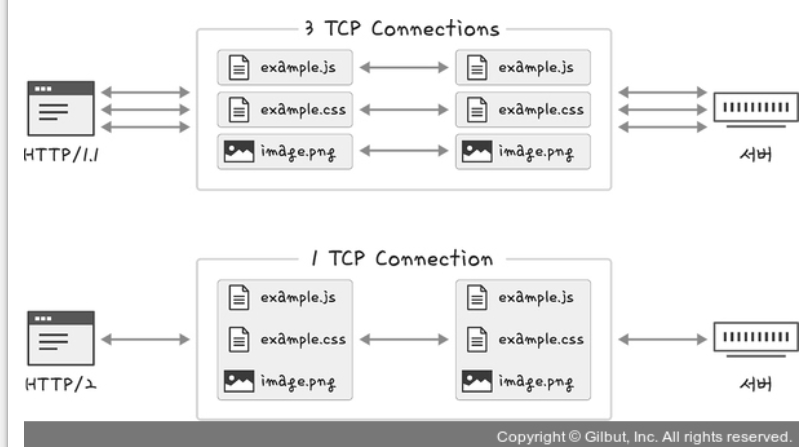
일 연결을 사용하여 병렬로 여러 요청을 받을 수 있고 응답을 줄 수 있다. 이렇게 되면 HTTP/1.x에서 발생하는 문제인 HOL Blocking을 해결할 수 있음.
헤더압축
앞서 말했듯 HTTP/1.1은 압축하지않고 많은 메타데이터를 포함하고있어 크기가 큼(무겁다)
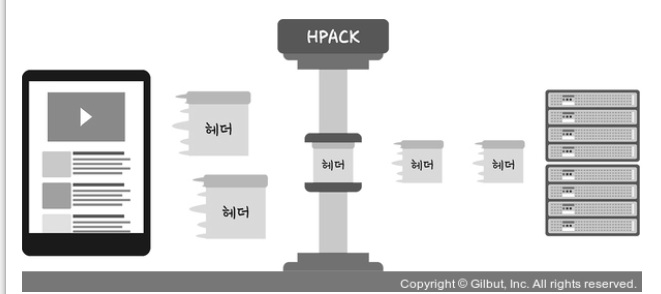
이를 HTTP/2에서는 헤더압축 써서 해결 허프만 코딩압축 알고리즘을 사용하는 HPACK압축 형식을가진다.
허프만 코딩
문자열을 문자단위로 쪼개 빈도수를 세어 빈도가 높은 정보는 적은 비트수 사용하여 표현
빈도가 낮은 정보는 비트수를 많이 사용하여 표현해서 전체 데이터의표현에 필요한 비트양을 줄이는 원리.
서버푸시
HTTP/1.1에서는 클라이언트 -> 서버 파일다운 O
HTTP/2 클라이언트 -> 서버 리소스 푸시O
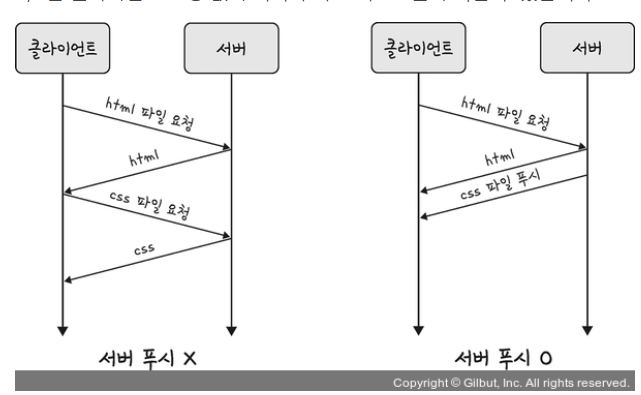
html 에는 css ,js파일이 포함 html을 읽으면서 그안에 들어있던 css파일을 서버에 푸시하여 클라이언트에 먼저 줄 수 있음.
4.HTTPS
HTTP/2는 HTTPS위에서 동작
HTTPS는 애플리케이션 계층과 전송계층 사이에 "신뢰계층"인 SSL/TLS계층을 넣은 신뢰할 수 있는 HTTP요청을 말함. = 통신암호화.
SSL/TLS
전송계층에서 보안을 제공하는 프로토콜
클라이언트와 서버가 통신할때 SSL/TLS를 통해 제 3자가 메시지를 도청,변조 못하도록함.
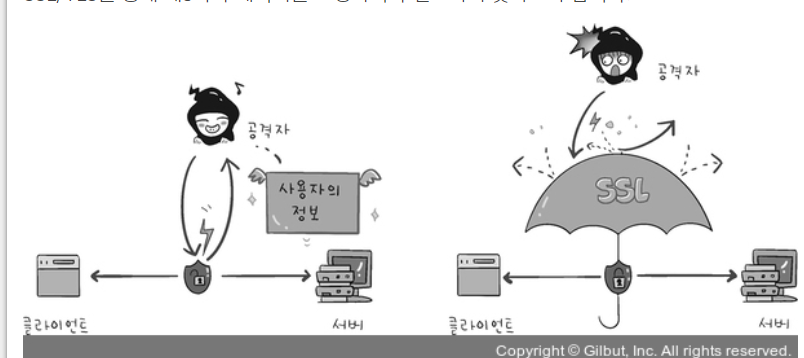
공격자가 서버인척 사용자 정보를 가로채는 네트워크상의 "인터셉터"를 방지.
SSL/TLS는 보안 세션을 기반으로 데이터를 "암호화"하며 보안세션이 만들어질때 인증메커니즘,키교환 암호화 알고리즘, 해싱 알고리즘 사용.
보안세션
보안이 시작되고 끝나는 동안 유지되는 세션.
SSL/TLS는 핸드셰이크를 통해 보안세션을 생성하고 이를 기반으로 상태정보 등을 공유.
세션
운영체제가 어떠한사용자로부터 자신의 자산이용을 허락하는 일정한 기간을 뜻함. 사용자는 일정시간동안 응용프로그램 자원등을 사용할 수 있음.
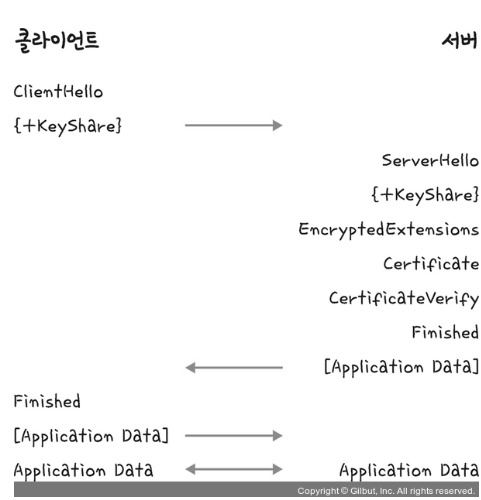
클라이언트와 서버와 키를 공유 - 이를기반으로 인증 ,인증확인 등의 작업이 일어나는 단 한번의 1-RTT가 생긴후 데이터 송수신.
클라이언트에 사이퍼 슈트를 서버에 전달하면 서버는 받은 사이퍼 슈트의 암호화 알고리즘 리스트를 제공할 수 있는지 확인.
제공가능하면 서버에 클라이언트로 인증서를 보내는 인증메커니즘 시작 이후 해싱알고리즘 등으로 암호화된 데이터의 송수신이 시작.
사이퍼 슈트
사이퍼 슈트는 프로토콜, AEAD 사이퍼 모드, 해싱 알고리즘이 나열된 규약을 말하며, 다섯 개가 있음.
• TLS_AES_128_GCM_SHA256
• TLS_AES_256_GCM_SHA384
• TLS_CHACHA20_POLY1305_SHA256
• TLS_AES_128_CCM_SHA256
• TLS_AES_128_CCM_8_SHA256
예를 들어 TLS_AES_128_GCM_SHA256에는 세 가지 규약이 들어 있는데 TLS는 프로토콜, AES_128_GCM은 AEAD 사이퍼 모드, SHA256은 해싱 알고리즘을 뜻함.
AEAD사이퍼 모드
데이터 암호화 알고리즘 이며, AES_128_GCM등 있음.
예를들어 AES_128_GCM 이란것은
128비트의 키를 사용하는 표준 블록 암호화 기술+
병렬계산에 용이한 암호화 알고리즘 GCM이 결합된 알고리즘.
인증메커니즘
CA(Certificate Authorities)에서 발급한 인증서를 기반으로 이루어짐. CA에서 발급한 인증서는 안전한 연결을 시작하는 데 있어 필요한 ‘공개키’를 클라이언트에 제공하고 사용자가 접속한 ‘서버가 신뢰’할 수 있는 서버임을 보장. 인증서는 서비스 정보, 공개키, 지문, 디지털 서명 등으로 이루어져 있음.
참고로 CA는 아무 기업이나 할 수 있는 것이 아니고 신뢰성이 엄격하게 공인된 기업들만 참여할 수 있으며, 대표적인 기업으로는 Comodo, GoDaddy, GlobalSign, 아마존 등이 있음.
CA발금 과정
자신의 서비스가 CA인증서를 발급 받으려면 자신의 사이트 정보와 공개키를 CA에 제출
이후 CA는 공개키를 해시한 값인 지문을 사용하는 CA의 비밀키 등을 기반으로 CA인증서 발급.
암호화 알고리즘
키교환 암호화 알고리즘으로는 대수곡선 기반의 ECDHE또는 모듈식 기반의 DHE를 사용.
둘다 디피-헬만방식을 근간.
디피-헬만 키교환 암호화 알고리즘.
암호화 키를 교환하는 하나의 방법.
Y = a^x mod p
p=소수 / g=생성자/ mod= 나눗셈의 나머지를 구하는 연산.
앞의 식에서 g와 x와 p를 안다면 y는 구하기 쉽지만
g와 y와 p만 안다면 x를 구하기는 어렵다는 원리에 기반한 알고리즘.
이러한 문제는 이산 대수 문제 라고 불리며 아직까지 이를 효율적으로 계산하는 방법은 수학적으로 알려져 있지 않다.
하나하나 대입해 보거나, 아무리 효율적인 알고리즘을 사용해도 지수적 시간 복잡도를 가지게 되는데,한쪽 방향으로만 계산하기 쉬운 일방향 함수는 바로 반쪽 짜리 키로 대칭 키를 만드는데 사용할 수 있음.
A= 개인 a키 이용 g^a mod p
B= 개인 b키 이용 g^b mod p
A =========> B
( g^a mod p)
B<==========A
(g^b mod p)
A 개인키 a이용 g^ab mod p
B 개인키 b이용 g^ab mod p
g^ab mod p - 대칭키(비밀키)생성
이사이 공격자는 g^(a+b) mod p 밖에 못만든다.
송수신자는 서로 반쪽짜리 키 인 a, b 를 직접 교환한 것 이 아닌 g^a mod p 와 g^b mod p 를 교환.
따라서 중간에 다른 사람(공격자)이 g^a mod p 와 g^b mod p 를 탈취해도, 이를 통해 서로를 곱한 g^(a+b) mod p 까지 만 얻을 수 있음.
이는 앞서 살펴본 이산 대수 문제로 설명이 가능한데.
이산 대수 문제는 y = g^x mod p 에서 g, p, x 가 알려져 있을때 y 를 계산하는 건 쉽지만, g, p, y 가 알려져 있을 때 역으로 x 를 구하는 방법은 어렵다.
따라서 다른 사람이 g^a mod p 와 g^b mod p 를 탈취해도, 이를 통해 반쪽 짜리 키 인 a, b 를 알아내기 어렵기 때문에 a, b 를 가지고 있는 데이터 송수신 자가 a, b 로 만든 대칭 키인 g^ab mod p 는 만들지 못하며, 아무리 노력해봐야 g^a mod p 와 g^b mod p 로 서로를 곱한 g^(a+b) mod p 까지 만 만들수 있다 가 증명.
결국, 대칭 키 인 g^ab mod p 를 만드려면 반쪽 짜리 키 원본인 a, b 를 알아야 한다.
이처럼 디피 헬만 키 교환 알고리즘은 이산 대수 문제라는 일방향 함수의 특징을 그대로 활용하여 만난 적도, 본 적도 없는 두 사람 만이 아는 비밀의 대칭 키를 만들어 내는 마법같은 알고리즘.
또한 정보가 중간에 탈취되도, 우리의 대칭키는 이산 대수 문제로 인해 탈취한 정보 만으로 만들기 어렵다는 것이 보장
단점으로는 상대방에 대한 인증 가능은x없고,
중간공격자에 취약.
디피-헬만 키교환 알고리즘
여담으로 텔레그램에 디-헬만 키교환 알고리즘이 적용 되어있다고 한다.
해싱 알고리즘
데이터를 추정하기 힘든 더 작고, 섞여있는 조각으로 만드는 알고리즘.
SSL/TLS는 해싱 알고리즘으로 SHA-256알고리즘과 SHA-384알고리즘을 쓰며 그중 많이 쓰는 SHA-256알고리즘을 보자.
SHA-256알고리즘
해시 함수의 결괏값이 256비트인 알고리즘.
비트코인을 비롯한 많은 블록체인 시스템에서 사용.
해싱을 해야할 메시지에 1을 추가하는 등 전처리를 하고 전처리된 메시지를 기반으로 해시를 반환.
해시
다양한 길이를 가진 데이터를 고정된 길이를 가진 데이터로 매핑한값.
해싱
임의의 데이터를 해시로 바꿔주는 일이며 해시 함수가 이를 담당.
해시 함수
임의의 데이터를 입력으로받아 일정한 길이의 데이터로 바꿔주는 함수.
참고로 TLS1.3은 사용자가 이전에 방문한 사이트로 다시 방문한다면 SSL/TLS에서 보안세션을 만들때 걸리는 통신 하지않아도됨 0-RTT
SEO에도 도움이 되는 HTTPS
구글은 SSL인증서를 강조했고 사이트내 모든 요소가 동일하다면 HTTPS서비스하는 사이트가 SEO순위가 높을거라 공식적으로 발표.
SEO(Search Engine Optimization)는 검색엔진 최적화란 뜻
사용자들이 구글 네이버 같은 검색엔진에 웹사이트를 검색했을때 페이지 상단에 노출 시켜 많은 사람이 볼 수 있게 최적화 하는방법을 의미.
많은 사람에게 노출시키는게 좋을것.
이를 위한 방법
- 캐노니컬 설정
- 메타설정
- 페이지 속도개선
- 사이트맵 관리
캐노니컬 설정
<link rel="canonical" href="https://example.com/page2.php" />사이트 link에 캐노니컬 설정해야함.
메타설정
html파일 가장 윗부분인 메타를 잘설정해야함.

페이지 속도개선
어떤 사이트를 들어갔는데 접속하는데만 10초가 걸리면 절대 이용 안하듯 페이지의 속도는 빨라야함. 구글의 PageSpeedInsights로 가서 자신의 서비스에 대한 리포팅을 주기적으로 받으며 관리해야함.
사이트맵 관리
사이트맵(sitemap.xml)을 정기적으로 관리하는 것은 필수입니다. 사이트맵 제너레이터를 사용하거나 직접 코드를 만들어 구축해도 됩니다. 사이트맵은 다음과 같은 형식의 xml 파일을 말함.
<?xml version="1.0" encoding="utf-8"?>
<urlset xmlns="http://www.sitemaps.org/schemas/sitemap/0.9">
<url>
<loc>http://kundol.co.kr/</loc>
<lastmod>수정날짜</lastmod>
<changefreq>daily</changefreq>
<priority>1.1</priority>
</url>
</urlset>HTTPS 구축방법
구축방법은 크게 세가지.
- 직접 CA에서 구매한 인증키를 기반으로 HTTPS서비스를 구축.
- 서버 앞단의 HTTPS를 제공하는 로드밸런서를 두기.
- 서버 앞단에 HTTPS를 제공하는 CDN을 둬서 구축.
5. HTTPS/3
HTTP/3은 HTTP/1.1 및 HTTP/2와 함께 World Wide Web에서 정보를 교환하는 데 사용되는 HTTP의 세 번째 버전.
TCP 위에서 돌아가는 HTTP/2와는 달리
HTTP/3은 QUIC이라는 계층 위에서 돌아가며, TCP 기반이 아닌 UDP 기반으로 돌아감.
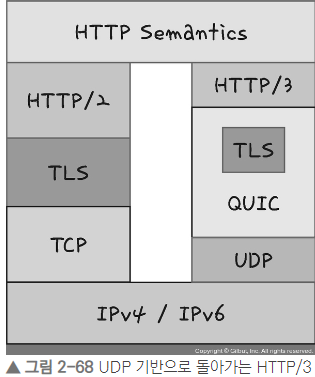
HTTP/2에서 장점이었던 멀티플렉싱을 가지고 있으며 초기 연결 설정 시 지연 시간 감소라는 장점.
초기 연결 설정 시 지연 시간 감소
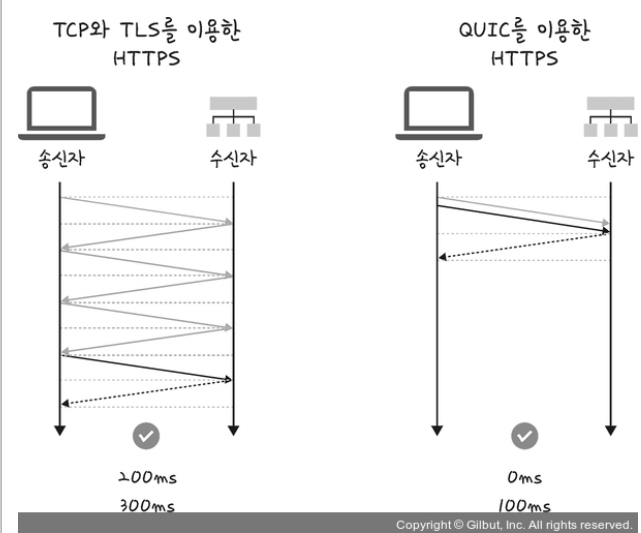
QUIC은 첫 연결 설정에 1-RTT만 소요.
참고로 QUIC은 순방향 오류 수정 메커니즘(FEC, Forword Error Correction)이 적용. 이는 전송한 패킷이 손실되었다면 수신 측에서 에러를 검출하고 수정하는 방식이며 열악한 네트워크 환경에서도 낮은 패킷 손실률을 자랑.