[Compiler] 2.2. Finite Automata

토큰 인식을 위한 구현
정규식의 형태로 지정된 패턴을 기반으로 입력을 Accept/Reject 함

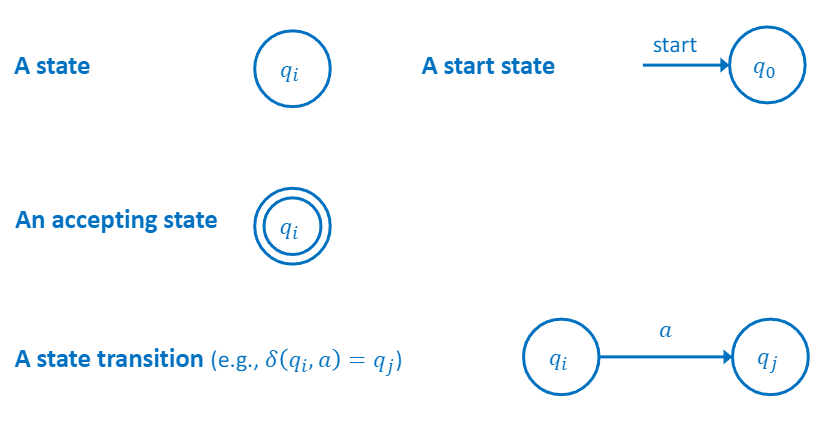
Finite Automata 정의

$M=\{Q,\Sigma,\delta,q_0,F\}$
state들의 유한집합 $Q=\{q_0,q_1,q_2,\dots ,q_i\}$
입력 기호의 집합, 입력 알파벳 $\Sigma$
초기 state $q_0$
최종 state $F$ ($F\subset Q$)
state transition function $\delta$
: $\delta(q_0,a)=q_1$ -> $q_0$에서 $a$ 입력되면 $q_1$으로 transition

그래프/도표 표기

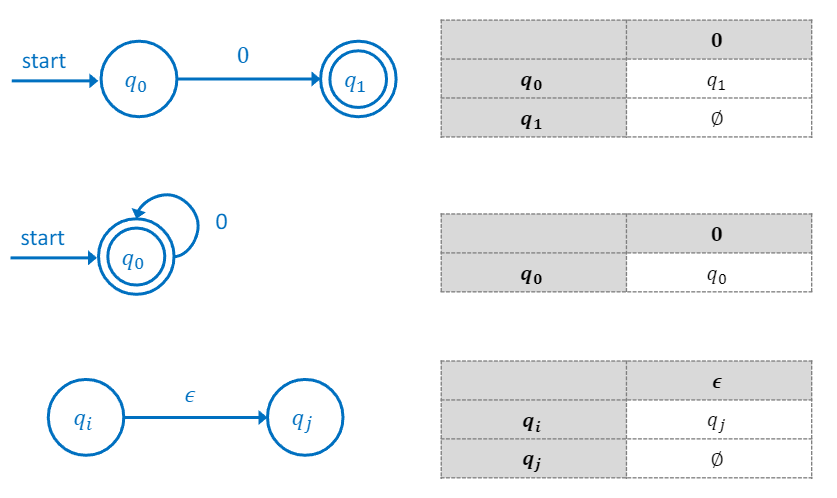
(왼쪽이 transition graph, 오른쪽이 transition table)

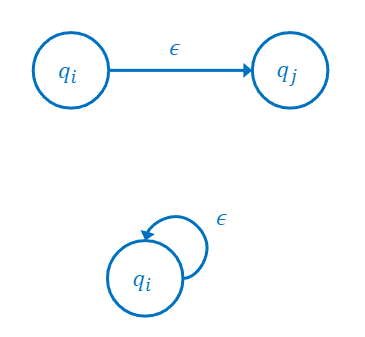
• epsilon-move: input 없이 이동할 수 있는 경우이다.
  

DFA vs NFA

• DFA: Deterministic Finite Automata
  (대부분) 하나의 state와 하나의 input symbol에 대해 하나의 transition만 존재.
  ε-move 금지
  빠른 실행
• NFA: Non-deterministic Finite Automata
  하나의 state와 하나의 input symbol에 대해 여러 transition 존재 가능
  ε-move 가능
  빠른 구현

McNaughtom-Yamada-Thompson alghrithm (aka Thomson's construction)

각 부분을 구현하고, ε-move로 묶는다.

• $r_1r_2$	$r_1 \| r_2$	$r_1^*$

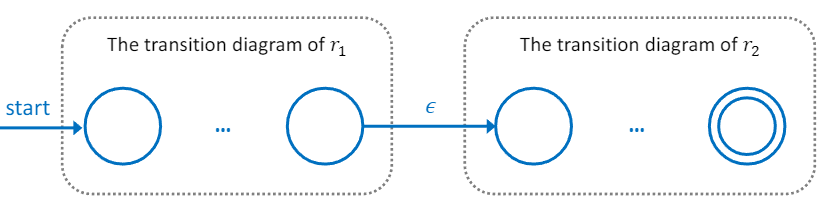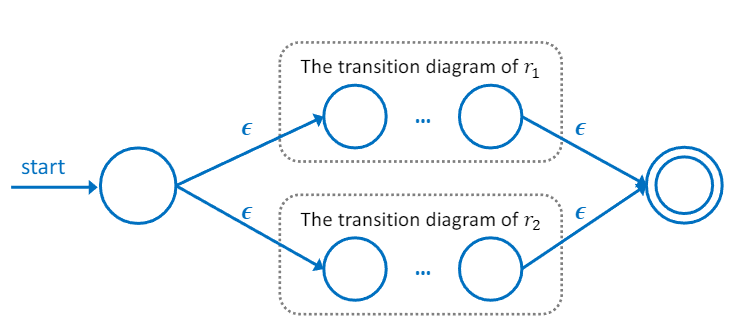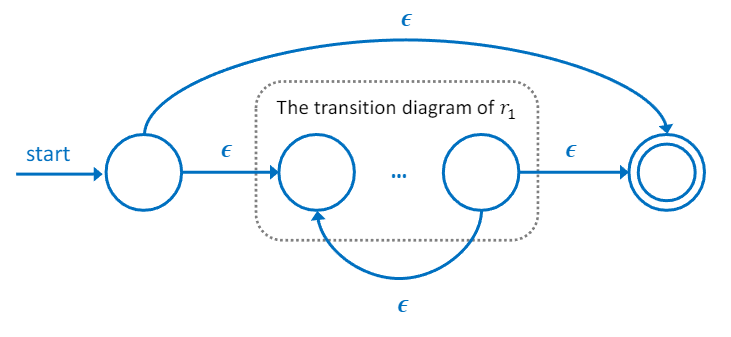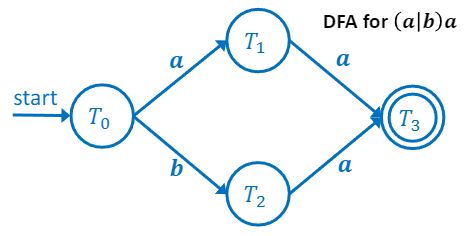
NFA - DFA 변환

• 용어 정의
  $\epsilon-closure(q^N) / \epsilon-colsure(T)$: state $q^N$ 또는 집합 $T$에서 ε-move로만 도달할 수 있는 state들의 집합. 자기 자신을 포함한다.

• 방법 & 예시
  

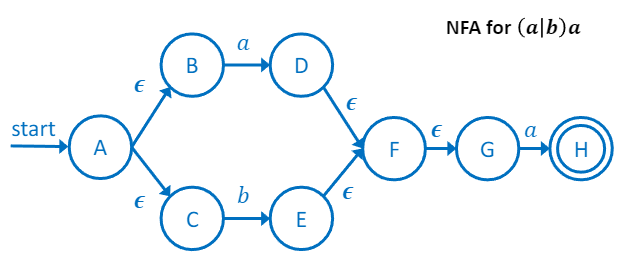
1. start state $q^N_0$로 부터, $\epsilon-closure(q^N_0)$ 계산
   $T_0 = \epsilon-closure(A) = \{A,B,C\}$

2. $s\in\Sigma$에 대해 $\epsilon-closure(\delta(T_0,s))$ 계산
   $T_1 = \epsilon-closure(\delta(T_0,a)) = \epsilon-closure(D) = \{D,F,G\}$
   $T_2 = \epsilon-closure(\delta(T_0,b)) = \epsilon-closure(E) = \{E,F,G\}$

3. 새로운 결과가 안나올 때 까지, $T_i$에 대해 2번 과정 반복
   $T_3 = \epsilon-closure(\delta(T_1,a)) = \epsilon-closure(H) = \{H\}$
   $\epsilon-closure(\delta(T_1,b)) = \empty$
   $\epsilon-closure(\delta(T_2,a)) = \{H\} (=T_3)$
   $\epsilon-closure(\delta(T_2,b)) = \empty$
   $\epsilon-closure(\delta(T_3,a)) = \empty$
   $\epsilon-closure(\delta(T_3,b)) = \empty$

4. 표 작성
   

5. 내용을 바탕으로 NFA 작성